- Research Article
- Open access
- Published:
On Complete Convergence for Weighted Sums of 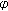 -Mixing Random Variables
-Mixing Random Variables
Journal of Inequalities and Applications volume 2010, Article number: 372390 (2010)
Abstract
Some results on complete convergence for weighted sums  are presented, where
are presented, where  ,
,  is a sequence of
is a sequence of  -mixing random variables and
-mixing random variables and  is an array of constants. They generalize the corresponding results for
is an array of constants. They generalize the corresponding results for  sequence to the case of
sequence to the case of  -mixing sequence.
-mixing sequence.
1. Introduction
Let  ,
,  be a sequence of random variables defined on a fixed probability space
be a sequence of random variables defined on a fixed probability space  . Let
. Let  and
and  be positive integers. Write
be positive integers. Write  ,
,  . Given
. Given  -algebras
-algebras  in
in  , let
, let

Define the  -mixing coefficients by
-mixing coefficients by

Definition 1.1.
A random variable sequence  ,
, is said to be a
is said to be a  -mixing random variable sequence if
-mixing random variable sequence if  as
as  .
.
 -mixing random variables were introduced by Dobrushin [1] and many applications have been found. See, for example, Dobrushin [1], Utev [2], and Chen [3] for central limit theorem, Herrndorf [4] and Peligrad [5] for weak invariance principle, Sen [6, 7] for weak convergence of empirical processes, Shao [8] for almost sure invariance principles, Hu and Wang [9] for large deviations, and so forth. When these are compared with the corresponding results of independent random variable sequences, there still remains much to be desired.
-mixing random variables were introduced by Dobrushin [1] and many applications have been found. See, for example, Dobrushin [1], Utev [2], and Chen [3] for central limit theorem, Herrndorf [4] and Peligrad [5] for weak invariance principle, Sen [6, 7] for weak convergence of empirical processes, Shao [8] for almost sure invariance principles, Hu and Wang [9] for large deviations, and so forth. When these are compared with the corresponding results of independent random variable sequences, there still remains much to be desired.
Throughout the paper, let  be the indicator function of the set
be the indicator function of the set  . We assume that
. We assume that  is a positive increasing function on
is a positive increasing function on  satisfying
satisfying  as
as  and
and  is the inverse function of
is the inverse function of  . Since
. Since  , it follows that
, it follows that  . For easy notation, we let
. For easy notation, we let  and
and  .
.  denotes that there exists a positive constant
denotes that there exists a positive constant  such that
such that  .
.  denotes a positive constant which may be different in various places.
denotes a positive constant which may be different in various places.
Let  ,
,  be a sequence of
be a sequence of  random variables and let
random variables and let  ,
,  be an array of constants. The almost sure limiting behavior of weighted sums
be an array of constants. The almost sure limiting behavior of weighted sums  was studied by many authors; see, for example, Choi and Sung [10], Cuzick [11], Wu [12], and Sung [13, 14], and so forth.
was studied by many authors; see, for example, Choi and Sung [10], Cuzick [11], Wu [12], and Sung [13, 14], and so forth.
The main purpose of this paper is to extend the complete convergence for weighted sums  of
of  random variables to the case of
random variables to the case of  -mixing random variables.
-mixing random variables.
Definition 1.2.
A sequence  of random variables is said to be stochastically dominated by a random variable
of random variables is said to be stochastically dominated by a random variable  if there exists a positive constant
if there exists a positive constant  , such that
, such that

for all  and
and  .
.
Definition 1.3.
A double array  ,
,  ,
,  of real numbers is said to be a Toeplitz array if
of real numbers is said to be a Toeplitz array if  for each
for each  and
and

for all  , where
, where  is a positive constant.
is a positive constant.
Lemma 1.4.
Let  ,
,  be a sequence of random variables which is stochastically dominated by a random variable
be a sequence of random variables which is stochastically dominated by a random variable  . For any
. For any  and
and  , the following statement holds:
, the following statement holds:

where  is a positive constant.
is a positive constant.
Lemma 1.5 (cf. [15, Lemma  ]).
]).
Let  ,
,  be a sequence of
be a sequence of  -mixing random variables. Let
-mixing random variables. Let  ,
,  ,
,  ,
,  , and
, and  . Then
. Then

Lemma 1.6 (cf. [8, Lemma 2.2]).
Let  ,
,  be a
be a  -mixing sequence. Put
-mixing sequence. Put  . Suppose that there exists an array
. Suppose that there exists an array  of positive numbers such that
of positive numbers such that

Then for every  , there exists a constant
, there exists a constant  depending only on
depending only on  and
and  such that
such that

for every  and
and  .
.
Lemma 1.7.
Let  ,
,  be a sequence of
be a sequence of  -mixing random variables satisfying
-mixing random variables satisfying  .
.  . Assume that
. Assume that  and
and  for each
for each  . Then there exists a constant
. Then there exists a constant  depending only on
depending only on  and
and  such that
such that

for every  and
and  . In particular, one has
. In particular, one has

for every  .
.
Proof.
By Lemma 1.5, we can see that

which implies (1.7). By Lemma 1.6, we can get the desired result (1.9) immediately. The proof is complete.
Lemma 1.8.
Assume that the inverse function  of
of  satisfies
satisfies

If  , then
, then

Proof.
The proof is similar to that of Lemma  by Sung [14]. So we omit it.
by Sung [14]. So we omit it.
2. Main Results and Their Proofs
Theorem 2.1.
Let  ,
,  be a sequence of identically distributed
be a sequence of identically distributed  -mixing random variables satisfying
-mixing random variables satisfying  ,
,  ,
,  , and
, and  . Assume that the inverse function
. Assume that the inverse function  of
of  satisfies (1.12). Let
satisfies (1.12). Let  ,
,  ,
,  be an array of constants such that
be an array of constants such that
(i) ;
;
(ii) for some
for some  .
.
Then for any  ,
,

Proof.
For each  , denote
, denote

It is easy to check that

Therefore

Firstly, we will show that

It follows from Lemma 1.8 and Kronecker's lemma that

By  , condition (i), (2.6), and
, condition (i), (2.6), and  , we can see that
, we can see that

which implies (2.5). By (2.4) and (2.5), we can see that, for sufficiently large  ,
,

To prove (2.1), it suffices to show that

By Markov's inequality, Lemma 1.7,  , and condition (ii), we have
, and condition (ii), we have

It follows from  that
that

We complete the proof of the theorem.
Theorem 2.2.
Let  ,
,  be a sequence of
be a sequence of  -mixing random variables satisfying
-mixing random variables satisfying  and let
and let  ,
,  ,
,  be an array of real numbers. Let
be an array of real numbers. Let  ,
,  be an increasing sequence of positive integers and let
be an increasing sequence of positive integers and let  ,
,  be a sequence of positive real numbers. If for some
be a sequence of positive real numbers. If for some  ,
,  , and for any
, and for any  , the following conditions are satisfied:
, the following conditions are satisfied:



then

Proof.
Note that if the series  is convergent, then (2.15) holds. Therefore, we will consider only such sequences
is convergent, then (2.15) holds. Therefore, we will consider only such sequences  ,
,  for which the series
for which the series  is divergent.
is divergent.
Let

Therefore

Using the  inequality and Jensen's inequality, we can estimate
inequality and Jensen's inequality, we can estimate  in the following way:
in the following way:

By (2.17), (2.18), and Lemma 1.7, we can get

Therefore, we can conclude that (2.15) holds by (2.12), (2.13), (2.14), and (2.19).
Theorem 2.3.
Let  and let
and let  ,
,  be a sequence of
be a sequence of  -mixing random variables satisfying
-mixing random variables satisfying  ,
,  , and
, and  for
for  . Let
. Let  ,
,  ,
,  be an array of real numbers satisfying the following condition:
be an array of real numbers satisfying the following condition:

for some  and
and  . Then for any
. Then for any  and
and  ,
,

Proof.
Take  ,
,  , and
, and  in Theorem 2.2. By (2.20) we have
in Theorem 2.2. By (2.20) we have

following from  . By the assumption
. By the assumption  for
for  and (2.20) we get
and (2.20) we get

following from  and
and  . We get the desired result by Theorem 2.2 immediately. The proof is completed.
. We get the desired result by Theorem 2.2 immediately. The proof is completed.
Theorem 2.4.
Let  and let
and let  ,
,  be a sequence of
be a sequence of  -mixing random variables satisfying
-mixing random variables satisfying  ,
,  , and
, and  for
for  . Assume that the random variables are stochastically dominated by a random variable
. Assume that the random variables are stochastically dominated by a random variable  such that
such that  and let
and let  ,
,  ,
,  be an array of real numbers satisfying the following condition:
be an array of real numbers satisfying the following condition:

for some  and
and  . Then for any
. Then for any  and
and  , (2.21) holds.
, (2.21) holds.
Proof.
The proof is similar to that of Theorem 2.3. We only need to note that

for each  .
.
Theorem 2.5.
Let  ,
,  be a sequence of
be a sequence of  -mixing random variables satisfying
-mixing random variables satisfying  and let
and let  ,
,  ,
,  be a Toeplitz array. Assume that the random variables are stochastically dominated by a random variable
be a Toeplitz array. Assume that the random variables are stochastically dominated by a random variable  . If for some
. If for some  and
and  ,
,

where  , then for any
, then for any  ,
,

Proof.
Take  ,
,  for
for  and
and  in Theorem 2.2. Then we can see that (2.12) and (2.13) are satisfied. In fact, by (1.4) and (2.26) we have
in Theorem 2.2. Then we can see that (2.12) and (2.13) are satisfied. In fact, by (1.4) and (2.26) we have

and by Lemma 1.4, (1.5), and (2.26) we have

In order to prove that (2.14) holds, we should consider the following two cases.
In the case  , by Lemma 1.4, (1.5), (2.26), and
, by Lemma 1.4, (1.5), (2.26), and  inequality, we have
inequality, we have

In the case  , we can get
, we can get

To complete the proof of the theorem, we only need to prove

Indeed, by Lemma 1.4, it follows that

Thus we get the desired result.
References
Dobrushin RL: The central limit theorem for non-stationary Markov chain. Theory of Probability and Its Applications 1956, 1: 72–88.
Utev SA: The central limit theorem for -mixing arrays of random variables. Theory of Probability and Its Applications 1990, 35(1):131–139. 10.1137/1135013
Chen DC: A uniform central limit theorem for nonuniform -mixing random fields. The Annals of Probability 1991, 19(2):636–649. 10.1214/aop/1176990445
Herrndorf N: The invariance principle for -mixing sequences. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete 1983, 63(1):97–108. 10.1007/BF00534180
Peligrad M: An invariance principle for -mixing sequences. The Annals of Probability 1985, 13(4):1304–1313. 10.1214/aop/1176992814
Sen PK: A note on weak convergence of empirical processes for sequences of -mixing random variables. Annals of Mathematical Statistics 1971, 42: 2131–2133. 10.1214/aoms/1177693079
Sen PK: Weak convergence of multidimensional empirical processes for stationary -mixing processes. The Annals of Probability 1974, 2(1):147–154. 10.1214/aop/1176996760
Shao QM: Almost sure invariance principles for mixing sequences of random variables. Stochastic Processes and Their Applications 1993, 48(2):319–334. 10.1016/0304-4149(93)90051-5
Hu S, Wang X: Large deviations for some dependent sequences. Acta Mathematica Scientia. Series B 2008, 28(2):295–300. 10.1016/S0252-9602(08)60030-2
Choi BD, Sung SH: Almost sure convergence theorems of weighted sums of random variables. Stochastic Analysis and Applications 1987, 5(4):365–377. 10.1080/07362998708809124
Cuzick J: A strong law for weighted sums of i.i.d. random variables. Journal of Theoretical Probability 1995, 8(3):625–641. 10.1007/BF02218047
Wu WB: On the strong convergence of a weighted sum. Statistics & Probability Letters 1999, 44(1):19–22. 10.1016/S0167-7152(98)00287-9
Sung SH: Strong laws for weighted sums of i.i.d. random variables. Statistics & Probability Letters 2001, 52(4):413–419. 10.1016/S0167-7152(01)00020-7
Sung SH: Strong laws for weighted sums of i.i.d. random variables. II. Bulletin of the Korean Mathematical Society 2002, 39(4):607–615.
Lu CR, Lin ZY: Limit Theory for Mixing Dependent Sequences. Science Press, Beijing, China; 1997.
Acknowledgments
The authors are most grateful to the Editor Andrei I. Volodin and anonymous referee for the careful reading of the manuscript and valuable suggestions which helped in significantly improving an earlier version of this paper. This work was supported by the National Natural Science Foundation of China (10871001, 60803059), Provincial Natural Science Research Project of Anhui Colleges (KJ2010A005), Talents Youth Fund of Anhui Province Universities (2010SQRL016ZD), and Youth Science Research Fund of Anhui University (2009QN011A).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xuejun, W., Shuhe, H., Wenzhi, Y. et al. On Complete Convergence for Weighted Sums of 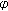 -Mixing Random Variables.
J Inequal Appl 2010, 372390 (2010). https://doi.org/10.1155/2010/372390
-Mixing Random Variables.
J Inequal Appl 2010, 372390 (2010). https://doi.org/10.1155/2010/372390
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/372390