- Research Article
- Open access
- Published:
On Jordan Type Inequalities for Hyperbolic Functions
Journal of Inequalities and Applications volume 2010, Article number: 362548 (2010)
Abstract
This paper deals with some inequalities for trigonometric and hyperbolic functions such as the Jordan inequality and its generalizations. In particular, lower and upper bounds for functions such as  and
and  are proved.
are proved.
1. Introduction
During the past several years there has been a great deal of interest in trigonometric inequalities [1–7]. The classical Jordan inequality [8, page 31]

has been in the focus of these studies and many refinements have been proved for it by Wu and Srivastava [9, 10], Zhang et al. [11], J.-L. Li and Y.-L. Li [5, 12], Wu and Debnath [13–15], Özban [16], Qi et al. [17], Zhu [18–29], Sándor [30, 31], Baricz and Wu [32, 33], Neuman and Sándor [34], Agarwal et al. [35], Niu et al. [36], Pan and Zhu [37], and Qi and Guo [38]. For a long list of recent papers on this topic see [7] and for an extensive survey see [17]. The proofs are based on familiar methods of calculus. In particular, a method based on a l'Hospital type criterion for monotonicity of the quotient of two functions from Anderson et al. [39] is a key tool in these studies. Some other applications of this criterion are reviewed in [40, 41]. Pinelis has found several applications of this criterion in [42] and in several other papers.
The inequality

where  is well-known and it was studied recently by Baricz in [43, page 111]. The second inequality of (1.2) is given in [8, page 354, 3.9.32] for
is well-known and it was studied recently by Baricz in [43, page 111]. The second inequality of (1.2) is given in [8, page 354, 3.9.32] for  For a refinement of the first inequality in (1.2) see Remark 1.3(1) and of the second inequality see Theorem 2.4.
For a refinement of the first inequality in (1.2) see Remark 1.3(1) and of the second inequality see Theorem 2.4.
This paper is motivated by these studies and it is based on the Master Thesis of Visuri [44]. Some of our main results are the following theorems.
Theorem 1.1.
For 

Theorem 1.2.
For 

We will consider quotients  and
and  at origin as limiting values
at origin as limiting values  and
and  .
.
Remark 1.3.
-
(1)
Let
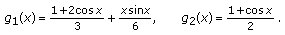 (1.5)
(1.5)
Then  on
on  because
because

In [45, ( )] it is proved that for
)] it is proved that for 

Hence  is a better lower bound for
is a better lower bound for  than (1.2) for
than (1.2) for  .
.
-
(2)
Observe that
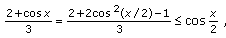 (1.8)
(1.8)
which holds true as equality if and only if  . In conclusion, (1.8) holds for all
. In conclusion, (1.8) holds for all  . Together with (1.2) we now have
. Together with (1.2) we now have

and by (1.8)

2. Jordan's Inequality
In this section we will find upper and lower bounds for  by using hyperbolic trigonometric functions.
by using hyperbolic trigonometric functions.
Theorem 2.1.
For 

Proof.
The lower bound of  holds true if the function
holds true if the function  is positive on
is positive on  . Since
. Since

we have  for
for  and
and  is increasing on
is increasing on  . Therefore
. Therefore

and the function  is increasing on
is increasing on  . Now
. Now  for
for  .
.
The upper bound of  holds true if the function
holds true if the function  is positive on
is positive on  . Let us denote
. Let us denote  . Since
. Since  for
for  we have
we have  and
and  for
for  . Now
. Now

which is positive on  , because
, because  and
and  for
for  . Therefore
. Therefore

for  . Now
. Now  for
for  .
.
Proof of Theorem 1.1.
The upper bound of  is clear by Theorem 2.1. The lower bound of
is clear by Theorem 2.1. The lower bound of  holds true if the function
holds true if the function  is positive on
is positive on  .
.
Let us assume  . Since
. Since  we have
we have  . We will show that
. We will show that

is positive which implies the assertion.
Now  is equivalent to
is equivalent to

Since  it is sufficient to show that
it is sufficient to show that  , which is equivalent to
, which is equivalent to

Let us denote  . Now
. Now  and therefore
and therefore  and
and  . Therefore inequality (2.8) holds for
. Therefore inequality (2.8) holds for  and the assertion follows.
and the assertion follows.
We next show that for  the upper and lower bounds of (1.2) are better than the upper and lower bounds in Theorem 2.1.
the upper and lower bounds of (1.2) are better than the upper and lower bounds in Theorem 2.1.
Theorem 2.2.
-
(i)
For
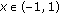
 (2.9)
(2.9)
-
(ii)
For
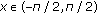
 (2.10)
(2.10)
-
(iii)
For
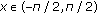

Proof.
-
(i)
The claim holds true if the function
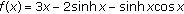 is nonnegative on
is nonnegative on  . By a simple computation we obtain
. By a simple computation we obtain 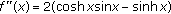 . Inequality
. Inequality 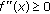 is equivalent to
is equivalent to  . By the series expansions of
. By the series expansions of 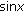 and
and 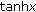 we obtain
we obtain 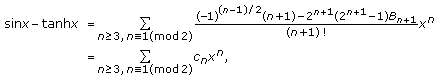 (2.12)
(2.12)
where  is the
is the  th Bernoulli number. By the properties of the Bernoullin numbers
th Bernoulli number. By the properties of the Bernoullin numbers  ,
,  , coefficients
, coefficients  , for
, for  , form an alternating sequence,
, form an alternating sequence,  as
as  and
and  for
for  . Therefore by Leibniz Criterion
. Therefore by Leibniz Criterion

and  for all
for all  . Now
. Now  is a convex function on
is a convex function on  and
and  is nondecreasing on
is nondecreasing on  with
with  . Therefore
. Therefore  is nondecreasing and
is nondecreasing and  .
.
-
(ii)
The claim holds true if the function
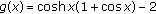 is nonnegative on
is nonnegative on 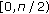 . By the series expansion of
. By the series expansion of  we have
we have  and therefore by the series expansion of
and therefore by the series expansion of 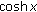
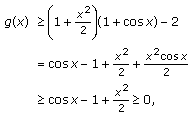 (2.14)
(2.14)
and the assertion follows.
-
(iii)
Clearly we have
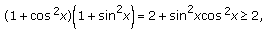 (2.15)
(2.15)
which implies the first inequality of the claim. The second inequality is trivial since  .
.
Theorem 2.3.
Let  . Then
. Then
(i)the function

is increasing on  ,
,
(ii)the function

is decreasing on  ,
,
(iii)the functions  and
and  are decreasing on
are decreasing on  .
.
Proof.
-
(i)
Let us consider instead of
 the function
the function 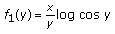 (2.18)
(2.18)
for  . Note that
. Note that  and therefore the claim is equivalent to the function
and therefore the claim is equivalent to the function  being decreasing on
being decreasing on  . We have
. We have

and  is equivalent to
is equivalent to  . Since
. Since  we have
we have  . Therefore
. Therefore  is increasing on
is increasing on  .
.
-
(ii)
We will consider instead of
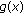 the function
the function 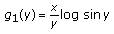 (2.20)
(2.20)
for  . Note that
. Note that  and therefore the claim is equivalent to the function
and therefore the claim is equivalent to the function  being increasing on
being increasing on  . We have
. We have

and  is equivalent to
is equivalent to  . Since
. Since  we have
we have  . Therefore
. Therefore  and the assertion follows.
and the assertion follows.
-
(iii)
We will show that
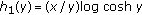 is increasing on
is increasing on 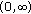 . Now
. Now  ,
, 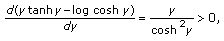 (2.22)
(2.22)
and  . Therefore the function
. Therefore the function  is increasing on
is increasing on  and
and  is decreasing on
is decreasing on  .
.
We will show that  is increasing on
is increasing on  . Now
. Now  ,
,

and  . Therefore the function
. Therefore the function  is increasing on
is increasing on  and
and  is decreasing on
is decreasing on  .
.
We next will improve the upper bound of (1.2).
Theorem 2.4.
For 

Proof.
The first inequality of (2.24) follows from (1.2).
By the series expansions of  and
and 

where the second inequality is equivalent to  and the second inequality of (2.24) follows.
and the second inequality of (2.24) follows.
By the identity  the upper bound of (2.24) is equivalent to
the upper bound of (2.24) is equivalent to  . By the series expansion of
. By the series expansion of 

and by the Leibniz Criterion the assertion follows.
3. Hyperbolic Jordan's Inequality
In this section we will find upper and lower bounds for the functions  and
and  .
.
Theorem 3.1.
For 

Proof.
We obtain from the series expansion of 

which proves the lower bound.
By using the identity  the chain of inequalities (1.2) gives
the chain of inequalities (1.2) gives

and the assertion follows from inequality  .
.
Remark 3.2.
J.-L. Li and Y.-L. Li have proved [12, (4.9)] that

where  This result improves Theorem 3.1.
This result improves Theorem 3.1.
Lemma 3.3.
For 
(i)
(ii)
(iii)
Proof.
-
(i)
For
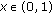 we have
we have 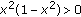 which is equivalent to
which is equivalent to 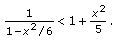 (3.5)
(3.5)
By Theorems 2.1, 3.1, and (3.5)

-
(ii)
Since
 for
for  we have
we have 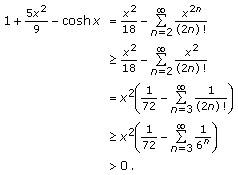 (3.7)
(3.7)
-
(iii)
By the series expansion of
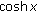 we have
we have 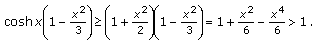 (3.8)
(3.8)
Proof of Theorem 1.2.
The lower bound of  follows from Lemma 3.3 and Theorem 3.1 since
follows from Lemma 3.3 and Theorem 3.1 since

The upper bound of  holds true if the function
holds true if the function  is positive on
is positive on  . By the series expansion it is clear that
. By the series expansion it is clear that

By Lemma 3.3 and (3.10)

and the assertion follows.
Theorem 3.4.
For 

Proof.
The upper bound of  holds true if the function
holds true if the function  is positive on
is positive on  . Since
. Since

we have

Therefore  and the assertion follows.
and the assertion follows.
Theorem 3.5.
For 

Proof.
The upper bound of  holds true if the function
holds true if the function  is positive on
is positive on  . Since
. Since  the function
the function  is increasing. Therefore
is increasing. Therefore  and
and  .
.
The lower bound of  holds true if the function
holds true if the function  is positive on
is positive on  . By the series expansions we have
. By the series expansions we have

By a straightforward computation we see that the polynomial  is strictly decreasing on
is strictly decreasing on  . Therefore
. Therefore

and the assertion follows.
Remark 3.6.
Baricz and Wu have shown in [33, page 276-277] that the right hand side of Theorem 2.1 is true for  and the right hand side of Theorem 3.5 is true for
and the right hand side of Theorem 3.5 is true for  . Their proof is based on the infinite product representations.
. Their proof is based on the infinite product representations.
Note that for 

Hence, the upper bound in Theorem 3.5 is better that in Theorem 3.4.
4. Trigonometric Inequalities
Theorem 4.1.
For  the following inequalities hold
the following inequalities hold
(i)
(ii)
(iii)
(iv)
Proof.
-
(i)
By setting
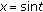 the assertion is equivalent to
the assertion is equivalent to 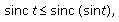 (4.1)
(4.1)
which is true because  is decreasing on
is decreasing on  and
and  .
.
-
(ii)
By the series expansions of
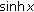 and
and  we have by Leibniz Criterion
we have by Leibniz Criterion 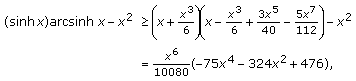 (4.2)
(4.2)
and since  on
on  the assertion follows.
the assertion follows.
-
(iii)
By the series expansions of
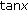 and
and  we have by Leibniz Criterion
we have by Leibniz Criterion  (4.3)
(4.3)
and since  on
on  the assertion follows.
the assertion follows.
-
(iv)
By the series expansions of
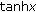 and
and  we have by Leibniz Criterion
we have by Leibniz Criterion

and since  on
on  the assertion follows.
the assertion follows.
Remark 4.2.
Similar inequalities to Theorem 4.1 have been considered by Neuman in [46, page 34-35].
Theorem 4.3.
Let  . Then
. Then
(i)for 

(ii)for 

(iii)for 

Proof.
-
(i)
The claim follows from the fact that
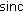 is decreasing on
is decreasing on 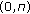 .
.
-
(ii)
The claim is equivalent to saying that the function
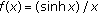 is increasing for
is increasing for  . Since
. Since 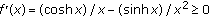 and
and  is equivalent to
is equivalent to 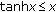 the assertion follows.
the assertion follows.
(iii)The claim is equivalent to  . By the series expansion of
. By the series expansion of  we have
we have

where  is the
is the  th Bernoulli number (
th Bernoulli number ( ,
,  ,
,  ). The assertion follows from the Leibniz Criterion, if
). The assertion follows from the Leibniz Criterion, if

for all  . Since (4.9) is equivalent to
. Since (4.9) is equivalent to

the assertion follows from the assumptions  and
and  .
.
References
Baricz Á: Redheffer type inequality for Bessel functions. Journal of Inequalities in Pure and Applied Mathematics 2007, 8(1, article 11):1–6.
Baricz Á: Jordan-type inequalities for generalized Bessel functions. Journal of Inequalities in Pure and Applied Mathematics 2008, 9(2, article 39):1–6.
Debnath L, Zhao C-J: New strengthened Jordan's inequality and its applications. Applied Mathematics Letters 2003, 16(4):557–560. 10.1016/S0893-9659(03)00036-3
Jiang WD, Yun H: Sharpening of Jordan's inequality and its applications. Journal of Inequalities in Pure and Applied Mathematics 2006, 7(3, article 102):1–4.
Li J-L: An identity related to Jordan's inequality. International Journal of Mathematics and Mathematical Sciences 2006, 2006:-6.
Wu S-H, Srivastava HM, Debnath L: Some refined families of Jordan-type inequalities and their applications. Integral Transforms and Special Functions 2008, 19(3–4):183–193.
Zhu L, Sun J: Six new Redheffer-type inequalities for circular and hyperbolic functions. Computers & Mathematics with Applications 2008, 56(2):522–529. 10.1016/j.camwa.2008.01.012
Mitrinović DS: Analytic Inequalities, Die Grundlehren der mathematischen Wissenschaften. Volume 16. Springer, New York, NY, USA; 1970:xii+400. in cooperation with P. M. Vasić
Wu S-H, Srivastava HM: A weighted and exponential generalization of Wilker's inequality and its applications. Integral Transforms and Special Functions 2007, 18(7–8):529–535.
Wu S-H, Srivastava HM: A further refinement of a Jordan type inequality and its application. Applied Mathematics and Computation 2008, 197(2):914–923. 10.1016/j.amc.2007.08.022
Zhang X, Wang G, Chu Y: Extensions and sharpenings of Jordan's and Kober's inequalities. Journal of Inequalities in Pure and Applied Mathematics 2006, 7(2, article 63):1–3.
Li J-L, Li Y-L: On the strengthened Jordan's inequality. Journal of Inequalities and Applications 2007, 2007:-8.
Wu S, Debnath L: A new generalized and sharp version of Jordan's inequality and its applications to the improvement of the Yang Le inequality. Applied Mathematics Letters 2006, 19(12):1378–1384. 10.1016/j.aml.2006.02.005
Wu S, Debnath L: A new generalized and sharp version of Jordan's inequality and its applications to the improvement of the Yang Le inequality. II. Applied Mathematics Letters 2007, 20(5):532–538. 10.1016/j.aml.2006.05.022
Wu S, Debnath L: Jordan-type inequalities for differentiable functions and their applications. Applied Mathematics Letters 2008, 21(8):803–809. 10.1016/j.aml.2007.09.001
Özban AY: A new refined form of Jordan's inequality and its applications. Applied Mathematics Letters 2006, 19(2):155–160. 10.1016/j.aml.2005.05.003
Qi F, Niu D-W, Guo B-N: Refinements, generalizations, and applications of Jordan's inequality and related problems. Journal of Inequalities and Applications 2009, 2009:-52.
Zhu L: Sharpening of Jordan's inequalities and its applications. Mathematical Inequalities & Applications 2006, 9(1):103–106.
Zhu L: Sharpening Jordan's inequality and the Yang Le inequality. Applied Mathematics Letters 2006, 19(3):240–243. 10.1016/j.aml.2005.06.004
Zhu L: Sharpening Jordan's inequality and Yang Le inequality. II. Applied Mathematics Letters 2006, 19(9):990–994. 10.1016/j.aml.2005.11.011
Zhu L: A general refinement of Jordan-type inequality. Computers & Mathematics with Applications 2008, 55(11):2498–2505. 10.1016/j.camwa.2007.10.004
Zhu L: General forms of Jordan and Yang Le inequalities. Applied Mathematics Letters 2009, 22(2):236–241. 10.1016/j.aml.2008.03.017
Zhu L: Sharpening Redheffer-type inequalities for circular functions. Applied Mathematics Letters 2009, 22(5):743–748. 10.1016/j.aml.2008.08.012
Zhu L: Some new inequalities of the Huygens type. Computers & Mathematics with Applications 2009, 58(6):1180–1182. 10.1016/j.camwa.2009.07.045
Zhu L: Some new Wilker-type inequalities for circular and hyperbolic functions. Abstract and Applied Analysis 2009, 2009:-9.
Zhu L: A source of inequalities for circular functions. Computers & Mathematics with Applications 2009, 58(10):1998–2004. 10.1016/j.camwa.2009.07.076
Zhu L: Generalized lazarevic's inequality and its applications—part II. Journal of Inequalities and Applications 2009, 2009:-4.
Zhu L: Jordan type inequalities involving the Bessel and modified Bessel functions. Computers & Mathematics with Applications 2010, 59(2):724–736. 10.1016/j.camwa.2009.10.020
Zhu L: Inequalities for hyperbolic functions and their applications. Journal of Inequalities and Applications. In press
Sándor J: On the concavity of . Octogon Mathematical Magazine 2005, 13(1):406–407.
Sándor J: A note on certain Jordan type inequalities. RGMIA Research Report Collection 2007., 10(1, article 1):
Baricz Á, Wu S: Sharp Jordan-type inequalities for Bessel functions. Publicationes Mathematicae Debrecen 2009, 74(1–2):107–126.
Baricz Á, Wu S: Sharp exponential Redheffer-type inequalities for Bessel functions. Publicationes Mathematicae Debrecen 2009, 74(3–4):257–278.
Neuman E, Sándor J: On some inequalities involving trigonometric and hyperbolic functions with emphasis on the Cusa-Huygens, Wilker, and Huygens inequalities. Mathematical Inequalities & Applications 2010, 1973: 1–9.
Agarwal RP, Kim Y-H, Sen SK: A new refined Jordan's inequality and its application. Mathematical Inequalities & Applications 2009, 12(2):255–264.
Niu D-W, Huo Z-H, Cao J, Qi F: A general refinement of Jordan's inequality and a refinement of L. Yang's inequality. Integral Transforms and Special Functions 2008, 19(3–4):157–164.
Pan W, Zhu L: Generalizations of Shafer-Fink-type inequalities for the arc sine function. Journal of Inequalities and Applications 2009, 2009:-6.
Qi F, Guo B-N: A concise proof of Oppenheim's double inequality relating to the cosine and sine functions. http://arxiv.org/abs/arxiv:0902.2511
Anderson GD, Vamanamurthy MK, Vuorine M: Conformal Invariants, Inequalities and Quasiconformal Mappings. John Wiley & Sons, New York, NY, USA; 1997.
Anderson GD, Vamanamurthy MK, Vuorinen M: Topics in special functions. In Papers on Analysis: A Volume Dedicated to Olli Martio on the Occasion of His 60th Birthday, Rep. Univ. Jyväskylä Dep. Math. Stat.. Volume 83. Edited by: Heinonen J, Kilpeläinen T, Koskela P. Univ. Jyväskylä, Jyväskylä, Finland; 2001:5–26.
Anderson GD, Vamanamurthy MK, Vuorinen M: Topics in special functions. II. Conformal Geometry and Dynamics 2007, 11: 250–270. 10.1090/S1088-4173-07-00168-3
Pinelis I: l'Hospital rules for monotonicity and the Wilker-Anglesio inequality. The American Mathematical Monthly 2004, 111(10):905–909. 10.2307/4145099
Baricz Á: Generalized Bessel functions of the first kind, Ph.D. thesis. Babes-Bolyai University, Cluj-Napoca, Romania; 2008.
Lehtonen M: Yleistetty konveksisuus, M.S. thesis. University of Turku; March 2008. written under the supervision of Prof. M. Vuorinen
Qi F, Cui L-H, Xu S-L: Some inequalities constructed by Tchebysheff's integral inequality. Mathematical Inequalities & Applications 1999, 2(4):517–528.
Neuman E: Inequalities involving inverse circular and inverse hyperbolic functions. Publikacije Elektrotehničkog Fakulteta Univerzitet u Beogradu. Serija Matematika 2007, 18: 32–37.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Klén, R., Visuri, M. & Vuorinen, M. On Jordan Type Inequalities for Hyperbolic Functions. J Inequal Appl 2010, 362548 (2010). https://doi.org/10.1155/2010/362548
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/362548
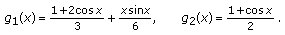
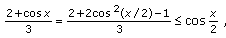
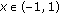

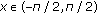

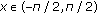
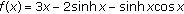 is nonnegative on
is nonnegative on  . By a simple computation we obtain
. By a simple computation we obtain 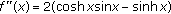 . Inequality
. Inequality 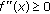 is equivalent to
is equivalent to  . By the series expansions of
. By the series expansions of 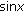 and
and 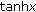 we obtain
we obtain 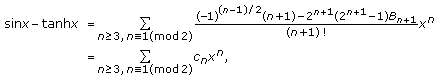
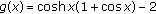 is nonnegative on
is nonnegative on 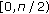 . By the series expansion of
. By the series expansion of  we have
we have  and therefore by the series expansion of
and therefore by the series expansion of 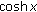
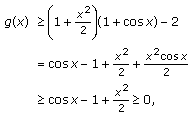
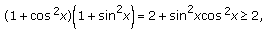
 the function
the function 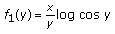
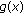 the function
the function 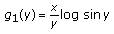
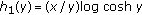 is increasing on
is increasing on  . Now
. Now  ,
, 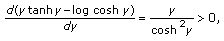
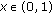 we have
we have 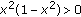 which is equivalent to
which is equivalent to 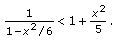
 for
for  we have
we have 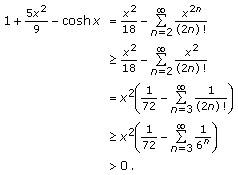
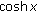 we have
we have 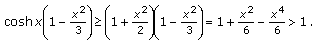
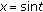 the assertion is equivalent to
the assertion is equivalent to 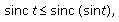
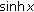 and
and  we have by Leibniz Criterion
we have by Leibniz Criterion 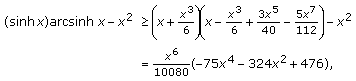
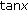 and
and  we have by Leibniz Criterion
we have by Leibniz Criterion 
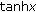 and
and  we have by Leibniz Criterion
we have by Leibniz Criterion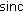 is decreasing on
is decreasing on 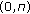 .
.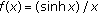 is increasing for
is increasing for  . Since
. Since 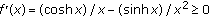 and
and  is equivalent to
is equivalent to 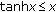 the assertion follows.
the assertion follows.