- Research Article
- Open access
- Published:
Some Nonlinear Weakly Singular Integral Inequalities with Two Variables and Applications
Journal of Inequalities and Applications volume 2010, Article number: 345701 (2010)
Abstract
Some nonlinear weakly singular integral inequalities in two variables which generalize some known results are discussed. The results can be used as powerful tools in the analysis of certain classes of differential equations, integral equations, and evolution equations. An example is presented to show boundedness of solution of a differential equation here.
1. Introduction
Various singular integral inequalities play an important role in the development of the theory of differential equations, functional differential equations, and integral equations. For example, Henry [1] proposed a linear integral inequality with singular kernel to investigate some qualitative properties for a parabolic differential equation, and Sano and Kunimatsu [2] gave a modified version of Henry type inequality. However, such results are expressed by a complicated power series which are sometimes inconvenient for their applications. To avoid the shortcoming of these results, Medveď [3] presented a new method to discuss nonlinear singular integral inequalities of Henry type and their Bihari version as follows:

and the estimates of solutions are given, respectively. In [4], Medveď also generalized his results to an analogue of the Wendroff inequalities for functions in two variables. From then on, more attention has been paid to such inequalities with singular kernel (see [5–9]). In particular, Ma and Yang [8] used a modification of Medveď method to obtain pointwise explicit bounds on solutions of more general weakly singular integral inequalities of the Volterra type, and later Ma and Pečarić [9] used this method to study nonlinear inequalities of Henry type. Recently, Cheung et al. [10] applied the modified Medveď method to investigate some new weakly singular integral inequalities of Wendroff type and applications to fractional differential and integral equations.
In this paper, motivated mainly by the work of Ma et al. [8, 9] and Cheung et al. [10], we discuss more general form of nonlinear weakly singular integral inequality of Wendroff type for functions in two variables

Our results can generalize some known results and be used more effectively to study the qualitative properties of the solutions of certain partial differential and integral equations. Moreover, an example is presented to show the usefulness of our results.
2. Main Result
In what follows,  denotes the set of real numbers, and
denotes the set of real numbers, and  .
.  denotes the collection of continuous functions from the set
denotes the collection of continuous functions from the set  to the set
to the set  .
.  and
and  denote the first-order partial derivatives of
denote the first-order partial derivatives of  with respect to
with respect to  and
and  , respectively.
, respectively.
Before giving our result, we cite the following definition and lemmas.
Definition 2.1 (see [8]).
Let  be an ordered parameter group of nonnegative real numbers. The group is said to belong to the first-class distribution and is denoted by
be an ordered parameter group of nonnegative real numbers. The group is said to belong to the first-class distribution and is denoted by  if conditions
if conditions  ,
,  , and
, and  are satisfied; it is said to belong to the second-class distribution and is denoted by
are satisfied; it is said to belong to the second-class distribution and is denoted by  if conditions
if conditions  ,
,  and
and  are satisfied.
are satisfied.
Lemma 2.2 (see [8]).
Let α,  ,
,  , and
, and  be positive constants. Then,
be positive constants. Then,

where  (
( ) is well-known
) is well-known  -function and
-function and  .
.
Lemma 2.3 (see [8]).
Suppose that the positive constants α,  ,
,  ,
,  , and
, and  satisfy the following conditions:
satisfy the following conditions:
(1)if  ,
,  ;
;
(2)if  ,
,  .
.
Then, for  ,
,

are valid.
Assume that
(A1) and
and  ;
;
(A2) is nondecreasing and
is nondecreasing and  .
.
Let  and
and  .
.
Theorem 2.4.
Under assumptions (A1) and (A2), if  satisfies (1.2), then
satisfies (1.2), then
-
(1)
for
 ,
,  (2.3)
(2.3)
for  and
and  , where
, where


is the inverse of  ,
,

and  are chosen such that
are chosen such that

-
(2)
for
 ,
, 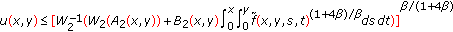 (2.7)
(2.7)
for  and
and  , where
, where


is the inverse of  ,
,

and  are chosen such that
are chosen such that

Proof.
With the definition of  and
and  , clearly,
, clearly,  and
and  are nonnegative and nondecreasing in
are nonnegative and nondecreasing in  and
and  . Furthermore,
. Furthermore,  and
and  . From (1.2), we have
. From (1.2), we have

Next, for convenience, we introduce indices  ,
,  . Denote that if
. Denote that if  , then let
, then let  and
and  ; if
; if  , then let
, then let  and
and  . Then
. Then  holds for
holds for  .
.
Using the Hölder inequality with indices  ,
,  to (2.11), we get
to (2.11), we get

By

from (2.12) and Lemma 2.2, we have

where

and  is given in Lemma 2.3 for
is given in Lemma 2.3 for  .
.
Since  and
and  (
( ), then
), then  and
and  are also nondecreasing in
are also nondecreasing in  and
and  . Taking any arbitrary
. Taking any arbitrary  and
and  with
with  ,
,  , we obtain
, we obtain

for  ,
,  . Denote
. Denote

and let

Then,  or
or  . Meanwhile,
. Meanwhile,  , and
, and  is nondecreasing in
is nondecreasing in  and
and  . Considering
. Considering

we have

where we apply the fact that  is nondecreasing in
is nondecreasing in  . Integrating both sides of the above inequality from 0 to
. Integrating both sides of the above inequality from 0 to  , we obtain
, we obtain

for  ,
,  , where
, where

From assumption (A2),  is strictly increasing so its inverse
is strictly increasing so its inverse  is continuous and increasing in its corresponding domain. Replacing
is continuous and increasing in its corresponding domain. Replacing  and
and  by
by  and
and  , we have
, we have

Since  and
and  are arbitrary, we replace
are arbitrary, we replace  and
and  by
by  and
and  , respectively, and get
, respectively, and get

for  and
and  . The above inequality can be rewritten as
. The above inequality can be rewritten as

Therefore, we have

for  and
and  .
.
Finally, considering two situations for  and using parameters α, β,
and using parameters α, β,  to denote
to denote  ,
,  ,
,  , and
, and  in the above inequality, we can obtain the estimations, respectively. we omit the details here.
in the above inequality, we can obtain the estimations, respectively. we omit the details here.
Remark 2.5.
Medveď[4, Theorem 2.2]investigated the special case( ,
,  )of inequality ( 1.2 ) under the assumption that "
)of inequality ( 1.2 ) under the assumption that " satisfies the condition
satisfies the condition ." However, in our result, the
." However, in our result, the condition is eliminated. If we take
condition is eliminated. If we take and
and , then we can obtain the result of linear case[4, Theorem 2.4].
, then we can obtain the result of linear case[4, Theorem 2.4].
Remark 2.6.
Let , then
, then or
or . Therefore, if we take
. Therefore, if we take , the formula(2.6)in[10]is the special case of inequality(1.2),and we can obtain more concise results than(2.7)and(2.9)in[10]. Moreover, here the condition
, the formula(2.6)in[10]is the special case of inequality(1.2),and we can obtain more concise results than(2.7)and(2.9)in[10]. Moreover, here the condition also can be eliminated.
also can be eliminated.
Remark 2.7.
When
 does not belong to
does not belong to
 or
or
 , there are some technical problems which we do not discuss here.
, there are some technical problems which we do not discuss here.
3. Some Corollaries
Corollary 3.1.
Let functions  ,
,  ,
,  be defined as in Theorem 2.4, and let
be defined as in Theorem 2.4, and let  be a constant with
be a constant with  . Suppose that
. Suppose that

Then,
-
(1)
for
 ,
,
if  ,
,

if  ,
,

for  ,
,  , where
, where  ,
,  ,
,  are defined as in Theorem 2.4,
are defined as in Theorem 2.4,
-
(2)
for
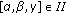 ,
,
if  ,
,

if  ,
,

for  ,
,  , where
, where  ,
,  ,
,  are defined as in Theorem 2.4.
are defined as in Theorem 2.4.
Proof.
Clearly, inequality (3.1) is the special case of (1.2). Taking  , we can get (3.1).
, we can get (3.1).
(i)If  ,
,

(ii)If  ,
,

Therefore, the positive numbers  and
and  in (2.6) and (2.10) can be taken as
in (2.6) and (2.10) can be taken as  , and the results can be obtained by simple computation. We omit the details.
, and the results can be obtained by simple computation. We omit the details.
Corollary 3.2.
Let functions  ,
,  ,
,  be defined as in Theorem 2.4. Suppose that
be defined as in Theorem 2.4. Suppose that  and
and  satisfies
satisfies

Then,
-
(i)
if
 ,
, 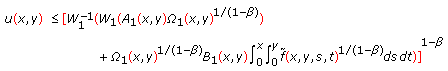 (3.9)
(3.9)
for  and
and  , where
, where


,  ,
,  ,
,  are defined as in Theorem 2.4, and
are defined as in Theorem 2.4, and  are chosen such that
are chosen such that

-
(ii)
if
 ,
, 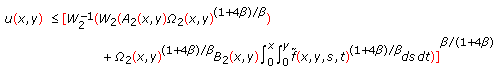 (3.12)
(3.12)
for  and
and  , where
, where


,  ,
,  ,
,  are defined as in Theorem 2.4, and
are defined as in Theorem 2.4, and  are chosen such that
are chosen such that

Proof.
By the two mentioned lemmas, it follows from (3.8) that

where  and
and

(i)For  ,
,
applying Corollary 3.1 to (3.15), we have

Letting

we get

Since inequality (3.19) is similar to (2.12), we can repeat the procedure of proof in Theorem 2.4 and get (3.9).
(ii)As for the case that  , the proof is similar to the argument in the proof of case (i) with suitable modification. We omit the details.
, the proof is similar to the argument in the proof of case (i) with suitable modification. We omit the details.
Remark 3.3.
When
 ,
,
 or
or
 ,
,
 , we can get the results which are similar to that in Corollary 3.2 and omit them here.
, we can get the results which are similar to that in Corollary 3.2 and omit them here.
4. Application
In this section, we will apply our result to discuss the boundedness of certain partial integral equation with weakly singular kernel.
Suppose that  satisfies the inequality as follow:
satisfies the inequality as follow:

for  ,
,  . Then, (4.1) is the special case of inequality (1.2) that is,
. Then, (4.1) is the special case of inequality (1.2) that is,

Obviously,  . Letting
. Letting  ,
,  , we have
, we have

Applying (2.3) in Theorem 2.4, we get for  ,
, 

which implies that  in (4.1) is bounded.
in (4.1) is bounded.
References
Henry D: Geometric Theory of Semilinear Parabolic Equations, Lecture Notes in Mathematics. Volume 840. Springer, Berlin, Germany; 1981:iv+348.
Sano H, Kunimatsu N: Modified Gronwall's inequality and its application to stabilization problem for semilinear parabolic systems. Systems & Control Letters 1994, 22(2):145–156. 10.1016/0167-6911(94)90109-0
Medveď M: A new approach to an analysis of Henry type integral inequalities and their Bihari type versions. Journal of Mathematical Analysis and Applications 1997, 214(2):349–366. 10.1006/jmaa.1997.5532
Medveď M: Nonlinear singular integral inequalities for functions in two and n independent variables. Journal of Inequalities and Applications 2000, 5(3):287–308. 10.1155/S102558340000014X
Dauer JP, Mahmudov NI: Integral inequalities and mild solutions of semilinear neutral evolution equations. Journal of Mathematical Analysis and Applications 2004, 300(1):189–202. 10.1016/j.jmaa.2004.06.040
Furati KM, Tatar N: Power-type estimates for a nonlinear fractional differential equation. Nonlinear Analysis: Theory, Methods & Applications 2005, 62(6):1025–1036. 10.1016/j.na.2005.04.010
Medveď M: Integral inequalities and global solutions of semilinear evolution equations. Journal of Mathematical Analysis and Applications 2002, 267(2):643–650. 10.1006/jmaa.2001.7798
Ma QH, Yang EH: Estimates on solutions of some weakly singular Volterra integral inequalities. Acta Mathematicae Applicatae Sinica 2002, 25(3):505–515.
Ma Q-H, Pečarić J: Some new explicit bounds for weakly singular integral inequalities with applications to fractional differential and integral equations. Journal of Mathematical Analysis and Applications 2008, 341(2):894–905. 10.1016/j.jmaa.2007.10.036
Cheung W-S, Ma Q-H, Tseng S: Some new nonlinear weakly singular integral inequalities of Wendroff type with applications. Journal of Inequalities and Applications 2008, 2008:-13.
Acknowledgments
This work is supported by Scientific Research Fund of Sichuan Provincial Education Department (no. 09ZC109). The authors are very grateful to the referees for their helpful comments and valuable suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, H., Zheng, K. Some Nonlinear Weakly Singular Integral Inequalities with Two Variables and Applications. J Inequal Appl 2010, 345701 (2010). https://doi.org/10.1155/2010/345701
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/345701
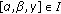 ,
, 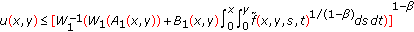
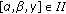 ,
, 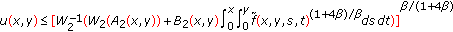
 ,
,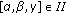 ,
, ,
, 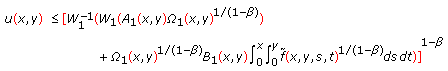
 ,
,