- Research Article
- Open access
- Published:
A Mathematical Revisit of Modeling the Majority Voting on Fixed-Income Quadratic Taxations
Journal of Inequalities and Applications volume 2010, Article number: 329378 (2010)
Abstract
Analyzing voting on income taxation usually implies mathematically cumbersome models. Moreover, a majority voting winner does not usually exist in such setups. Therefore, it is important to mathematically describe those cases in which a majority winner exists, at least for the basic models of voting on income taxation. We provide a complete mathematical description of those income distribution functions for which a majority winning tax exists (or does not exist), in the quadratic taxation model à la Roemer (1999), with tax schedules that are not necessarily purely redistributive. As an intermediate step, we identify by the corner method what are the most preferred taxes of the individuals, when taxation is not purely redistributive. Finally, we prove that for both purely and nonpurely redistributive quadratic taxations, the sufficient inequality condition of De Donder and Hindriks (2004) on the income distribution functions, for the existence of a Condorcet winner, can be relaxed to a broader condition.
1. Introduction
One important question that the positive theory of income taxation tries to answer is why marginal-rate progressive tax schedules are preponderant in democracies. An heuristic argument commonly invoked to explain this stylized fact resides in the observation that in general, the number of relatively poor (self-interest) voters exceeds that of richer ones. Nevertheless, mathematically formalizing the argument is not an easy task and the literature is rather inconclusive in this respect.
One very important difficulty which arises when studying these issues is that usually the existence of a majority winner (i.e., Condorcet winner) is not guaranteed. Voting games over redistributive tax schedules lack in general the existence of a static equilibrium (see Marhuenda and Ortuño-Ortin [1], Hindriks [2], De Donder and Hindriks [3]). The seminal papers of Romer [4, 5] and Roberts [6] consider only flat rate taxes in order to make use of the median voter theorem, after imposing some natural additional restrictions. However, the overrestrictive assumption of linear tax schemes does not provide the framework to investigate important issues like the high prevalence of marginal-rate progressive taxations in democracies. Therefore, many authors study the basic problem of voting on income taxations in terms of larger classes of tax functions.
Gouveia and Oliver [7] work with two-bracket piecewise linear functions, Cukierman and Meltzer [8] and Roemer [9] study quadratic tax functions, while Carbonell and Klor [10] consider a representative democracy model that allows for the class of all piecewise linear tax schedules. Marhuenda and Ortuño-Ortin [11] allow for the class of all concave or convex tax functions, proving by Jensen's inequality that for income distributions with the median below the mean income, any concave tax scheme receives less popular support than any convex tax scheme.
Carbonell and Ok [12] provide a two-party voting game in which each party (whose objective is to win the elections) proposes tax schemes from an unrestricted set of admissible functions and the voters selfishly vote for the tax that taxes them less. Establishing the existence of mixed equilibria, they identify certain cases in which marginal-rate progressive taxes are chosen almost surely by the political parties. However, Carbonell and Ok [12] find that if the tax policy space is not artificially constrained, the support of at least one equilibrium cannot be obtained within the set of marginal-rate progressive taxes. This result is in the same line with the one of Klor [13], who shows that a majority of poor voters does not necessarily imply progressive taxation for a more general policy space than the one in Marhuenda and Ortuño-Ortin [11].
Although it is hard to find an economically meaningful way of restricting the admissible set of income tax functions, the literature on voting over income taxes which are chosen from restricted policy spaces provides useful and powerful insights into the general problem. In particular, the quadratic model was very much used in the literature to generate interesting results. Cukierman and Meltzer [8] analyze the conditions under which the median voter's most preferred tax policy is a majority winner, in quadratic distortionary tax environments. Roemer [9] uses the quadratic taxation framework to define a different solution concept than the majority winner, based on the need to reach an intraparty agreement between the "opportunists" and the "militants" of the parties. In the same setup of fixed income (i.e., income not distorted by taxes) and quadratic taxations as the one in Roemer [9], Hindriks [2] establishes the inevitable vote cycling theorem.
De Donder and Hindriks [14] introduce preferences for leisure in the quadratic taxation model and study the voting process over tax schedules using other political equilibria than the Condorcet winner. For the quadratic model with fixed income, De Donder and Hindriks [3] show that incentive constraints result in the policy set to be closed and that individuals all have corner solutions over this set. They also provide a necessary and sufficient condition on the income distribution such that a Condorcet winner exists. Moreover, for income distributions with the median less than the mean, if a majority winner exists then it involves maximum progressivity.
This paper provides a complete description of those income distribution functions for which a majority winning tax exists (or does not exist), when the quadratic taxation model is not purely redistributive. For reasons of completeness, the analysis is not limited only to right skewed income distributions (which are empirically predominant), but there has been also considered the case of the left skewed income distributions. We also identify what are the most preferred taxes of the individuals (and the corresponding income groups they can be classified in, based on the preferred policies), when taxation has more than a purely redistributive purpose. Moreover, we show in this paper that the sufficient condition of De Donder and Hindriks [3], imposed on the income distribution functions in order to insure the existence of a Condorcet winner, can be relaxed to a broader condition.
The paper is organized as follows. Section 2 presents the model. Section 3 states and proves the results. Section 4 discusses and draws the conclusions.
2. The Model
The economy consists of a large number of individuals who differ in their (fixed) income. Each individual is characterized by his/her income  . The income distribution can be described by a continuous function
. The income distribution can be described by a continuous function  , differentiable almost everywhere and strictly increasing on the interval
, differentiable almost everywhere and strictly increasing on the interval  . Each individual with income
. Each individual with income  has strictly increasing preferences on the set of its possible net incomes. For any Lebesque measurable set
has strictly increasing preferences on the set of its possible net incomes. For any Lebesque measurable set  , the associated Lebesque-Stieltjes probability measure induced by
, the associated Lebesque-Stieltjes probability measure induced by  is denoted by
is denoted by  and it is defined as
and it is defined as  .
.
For better comprehensibility of the text, any parameter calculated based on the distribution  is denoted using the letter
is denoted using the letter  (e.g., the mean is
(e.g., the mean is  , the median is denoted by
, the median is denoted by  , the noncentered moment of second order is
, the noncentered moment of second order is  , and the variance of the income distribution is
, and the variance of the income distribution is  ), while
), while  refers to a random income in the interval
refers to a random income in the interval  .
.
The fixed amount  should be collected through means of a tax imposed on the agents. When
should be collected through means of a tax imposed on the agents. When  , the tax is purely redistributive. It is assumed that there is no tax evasion, and there are no distortions induced by the taxation system in the economy (i.e., the income is fixed), respectively. The set of admissible tax functions satisfies certain conditions. For a given
, the tax is purely redistributive. It is assumed that there is no tax evasion, and there are no distortions induced by the taxation system in the economy (i.e., the income is fixed), respectively. The set of admissible tax functions satisfies certain conditions. For a given  and
and  ,
,  denotes the set of all functions
denotes the set of all functions  such that (without the second and third conditions below, we would have a resource redistribution problem like in Grandmont [15], which is known not to have a Condorcet winner; see at the end of this section the definition for a majority winner.)
such that (without the second and third conditions below, we would have a resource redistribution problem like in Grandmont [15], which is known not to have a Condorcet winner; see at the end of this section the definition for a majority winner.)
(1) , for all
, for all  ;
;
(2) , for all
, for all  ;
;
(3) , for all
, for all  ;
;
(4)
A tax schedule is (marginally) progressive (regressive) if and only if  is convex (concave). In the following, we consider only quadratic taxes of the form
is convex (concave). In the following, we consider only quadratic taxes of the form  ,
,  . (The analysis also includes the case of linear tax schedules, when the coefficient "
. (The analysis also includes the case of linear tax schedules, when the coefficient " " takes the zero value.) We restrict our analysis to
" takes the zero value.) We restrict our analysis to  , the set of quadratic tax functions that satisfy the feasibility conditions (1)–(4). It can be easily proved that conditions (1) to (4) restrict the set of quadratic feasible taxes to functions of the form
, the set of quadratic tax functions that satisfy the feasibility conditions (1)–(4). It can be easily proved that conditions (1) to (4) restrict the set of quadratic feasible taxes to functions of the form  ,
,  , which satisfy the following conditions:
, which satisfy the following conditions:

Note that for every given distribution  and feasible
and feasible  , to every tax
, to every tax  from
from  , it corresponds one and only one element
, it corresponds one and only one element  in the feasible area (FA), and vice versa. Thus, the set of feasible quadratic tax policies
in the feasible area (FA), and vice versa. Thus, the set of feasible quadratic tax policies  can be illustrated as follows (the intervals for
can be illustrated as follows (the intervals for  are mathematically well defined due to the inequality
are mathematically well defined due to the inequality  , more specifically from
, more specifically from  .)
.)
(i)The case  is represented in Figure 1(a).
is represented in Figure 1(a).
(ii)The case  is represented in Figure 1(b).
is represented in Figure 1(b).
-
(iii)
The case
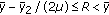 is represented in Figure 1(c).
is represented in Figure 1(c).
The coordinates of the vertices of the above polygons are easily obtained by elementary computations and are given by
progressive taxations:  ,
,  ,
,  ,
,
regressive taxations:  ,
,  ,
,  ,
,
no taxation:  , confiscation policy:
, confiscation policy:  .
.
Figure 1 presents the feasibility areas for different cases of the collected amount  . These areas are determined by the (FA) conditions as follows: the first two conditions determine the interior and the sides of the
. These areas are determined by the (FA) conditions as follows: the first two conditions determine the interior and the sides of the  parallelogram. The third condition is the tax revenue requirement constraint, graphically identified by the half-plane situated above the line
parallelogram. The third condition is the tax revenue requirement constraint, graphically identified by the half-plane situated above the line  .
.
For the case depicted in Figure 1(a), the tax  is the most progressive,
is the most progressive,  is the most regressive, and
is the most regressive, and  and
and  are out of the feasible area (FA). If
are out of the feasible area (FA). If  then
then  is not feasible, while if
is not feasible, while if  then
then  . For the case depicted in Figure 1(b), the tax policy
. For the case depicted in Figure 1(b), the tax policy  is the most progressive,
is the most progressive,  is the most regressive, and the tax policies
is the most regressive, and the tax policies  ,
,  ,
,  ,
,  are not feasible. For the case depicted in Figure 1(c), the tax schedule
are not feasible. For the case depicted in Figure 1(c), the tax schedule  is the most progressive,
is the most progressive,  is the most regressive, and the tax policies
is the most regressive, and the tax policies  ,
,  ,
,  ,
,  are not feasible.
are not feasible.
A majority (or Condorcet) winning tax policy is a pair  in the feasible set such that is preferred by a majority of individuals to any other feasible pair
in the feasible set such that is preferred by a majority of individuals to any other feasible pair  in
in  . An equivalent definition used in our proofs is the following: a tax function is a majority winner if and only if there is no objection to it (given
. An equivalent definition used in our proofs is the following: a tax function is a majority winner if and only if there is no objection to it (given  , a tax policy
, a tax policy  is an objection to
is an objection to  if
if  ). We denote by
). We denote by  the set of all objections to the taxation function
the set of all objections to the taxation function  . Therefore, the above definitions for
. Therefore, the above definitions for  being a Condorcet winner are equivalent to the condition
being a Condorcet winner are equivalent to the condition  .
.
If  , by considering
, by considering  and
and  , De Donder and Hindriks [3] defined the low middle and large income groups which are obtained based on the three intervals
, De Donder and Hindriks [3] defined the low middle and large income groups which are obtained based on the three intervals  and
and  divide
divide  . Note as well that
. Note as well that  . Nevertheless, the other two fixed values of the income are important for the analysis that follows. Those values are
. Nevertheless, the other two fixed values of the income are important for the analysis that follows. Those values are  . In the same spirit as the interpretation offered by De Donder and Hindriks [3], the voters
. In the same spirit as the interpretation offered by De Donder and Hindriks [3], the voters  are poor with relatively high income, and
are poor with relatively high income, and  are rich voters with relatively low income, respectively. As one can see in the section of results, these values will play an important role for stating the necessary and sufficient conditions for the existence of a Condorcet winner in the described environment.
are rich voters with relatively low income, respectively. As one can see in the section of results, these values will play an important role for stating the necessary and sufficient conditions for the existence of a Condorcet winner in the described environment.
3. Results
In order to identify the majority winning tax policies (if any), the first step is to characterize the tax policies  that are objections to a given tax policy
that are objections to a given tax policy  . Therefore, we need first to determine the sign of the function
. Therefore, we need first to determine the sign of the function  on the interval
on the interval  and then to find the Lebesgue measure
and then to find the Lebesgue measure  of the set
of the set  on which the difference function is negative. The following lemma presents the way in which the two roots of the quadratic function
on which the difference function is negative. The following lemma presents the way in which the two roots of the quadratic function  vary. Since the difference function is
vary. Since the difference function is  ,
,  , then it is sufficient to study the sign of the following quadratic function:
, then it is sufficient to study the sign of the following quadratic function:  ,
,  ,
,  . (We will analyze in the lemma only the case when
. (We will analyze in the lemma only the case when  ; the case
; the case  will be discussed separately each time when it occurs in our discussion.)
will be discussed separately each time when it occurs in our discussion.)
Lemma 3.1.
Let  ,
,  ,
,  , and
, and  , and let
, and let  . Then, for each
. Then, for each  , the quadratic function
, the quadratic function  has two real roots
has two real roots  and
and  , which vary as functions of
, which vary as functions of  as it is shown in Table 1, where
as it is shown in Table 1, where  and
and  .
.
 and
and  .
.Proof of Lemma 3.1.
The discriminant of  can be written as
can be written as  ; hence
; hence  has two real roots. For each
has two real roots. For each  , we will denote by
, we will denote by  and by
and by  the smallest and, respectively the largest of the roots. After short computations, we get
the smallest and, respectively the largest of the roots. After short computations, we get  and
and  .
.
The behavior of the roots as functions of  can be elementary studied by computing their derivatives and the limits at the endpoints of
can be elementary studied by computing their derivatives and the limits at the endpoints of  . Since
. Since  , for each
, for each  and
and  , for each
, for each  , then
, then  and
and  are increasing functions of
are increasing functions of  . The limits of the functions
. The limits of the functions  and
and  at the endpoints of the definition domain are
at the endpoints of the definition domain are  ,
,  ,
,  ,
,  .
.
Elementary computations give us the following results:  ,
,  ,
,  ,
,  ,
,  , and
, and  . Due to the previous computations, the behavior of the functions
. Due to the previous computations, the behavior of the functions  and
and  is as presented in Table 1.
is as presented in Table 1.
The purely redistributive tax policies that individuals prefer are described in De Donder and Hindriks [3]; all individuals in the same income class prefer the same policy. The low income group prefers confiscation policy (represented by the point  in the feasible region (FA) when
in the feasible region (FA) when  ), the middle income class prefers the maximum progressivity (represented by the point
), the middle income class prefers the maximum progressivity (represented by the point  if
if  ), and no taxation (the point
), and no taxation (the point  ) is preferred by the high income group. The next lemma shows how this simple description changes when the tax schedules are not purely redistributive. A sketch of the proof is provided after stating the result and further details are available upon request.
) is preferred by the high income group. The next lemma shows how this simple description changes when the tax schedules are not purely redistributive. A sketch of the proof is provided after stating the result and further details are available upon request.
Lemma 3.2.
The preferred tax for an individual with the income  is
is
(1)the case  (Figure 1(a)):
(Figure 1(a)):
(1a)  for
for  (for the income
(for the income  , the individual is indifferent between the taxes on the segment
, the individual is indifferent between the taxes on the segment  ),
),
(1b)  for
for  (for the income
(for the income  , the individual is indifferent between the taxes on the segment
, the individual is indifferent between the taxes on the segment  ),
),
(1c)  for
for  (for the income
(for the income  , the individual is indifferent between the taxes on the segment
, the individual is indifferent between the taxes on the segment  ),
),
(1d)  for
for  ,
,
(2)the case  (Figure 1(b)):
(Figure 1(b)):
(2a)  for
for  (for the income
(for the income  , the individual is indifferent between the taxes on the segment
, the individual is indifferent between the taxes on the segment  ),
),
(2b)  for
for  (for the income
(for the income  , the individual is indifferent between the taxes on the segment
, the individual is indifferent between the taxes on the segment  ),
),
(2c) similar to (1d),
(3)the case  (Figure 1(c)):
(Figure 1(c)):
(3a) similar to (2a),
(3b)  for
for  (for the income
(for the income  , the individual is indifferent between the taxes on the segment
, the individual is indifferent between the taxes on the segment  ),
),
(3c)  for
for  .
.
Proof of Lemma 3.2.
An individual with income  prefers the tax
prefers the tax  for which the difference
for which the difference  is maximum. Hence, we have to solve the following linear programming problem: determine the maximum of the function
is maximum. Hence, we have to solve the following linear programming problem: determine the maximum of the function  , subject to the constraints
, subject to the constraints  ,
,  ,
,  ,
,  . The problem can be elementary solved by using the corner method.
. The problem can be elementary solved by using the corner method.
Irrespective of the amount  that should be collected, the low income group prefers the tax policy that equalizes the posttax income. The middle income group prefers the most progressive tax policy. The high income group is divided in a lower part and an upper one by the value
that should be collected, the low income group prefers the tax policy that equalizes the posttax income. The middle income group prefers the most progressive tax policy. The high income group is divided in a lower part and an upper one by the value  . The upper part always prefers a regressive taxation when
. The upper part always prefers a regressive taxation when  (in fact, for high values of the amount to be collected, this income group prefers the most regressive tax schedule—see Lemma 3.2(3c)) above). The lower part of the high income group usually behaves as the middle income group, except for the case of low levels of
(in fact, for high values of the amount to be collected, this income group prefers the most regressive tax schedule—see Lemma 3.2(3c)) above). The lower part of the high income group usually behaves as the middle income group, except for the case of low levels of  . Even in such a case (see Lemma 3.2(1c)), the lower part of the high income group prefers a progressive taxation instead of a regressive one. These observations motivate a possible redefinition of the middle income group from
. Even in such a case (see Lemma 3.2(1c)), the lower part of the high income group prefers a progressive taxation instead of a regressive one. These observations motivate a possible redefinition of the middle income group from  to
to  . However, in order to have clear comparisons between the results in De Donder and Hindriks [3] and our results, we consider
. However, in order to have clear comparisons between the results in De Donder and Hindriks [3] and our results, we consider  as the lower part of the high income group, while the interval
as the lower part of the high income group, while the interval  keeps its interpretation of middle income class.
keeps its interpretation of middle income class.
Having Lemmas 3.1 and 3.2 at hand, we are in the position to provide a complete description of the cases in which there is a majority winning tax, or when there is not. The next proposition can be immediately obtained from the lemmas and it is a first step to provide such a description.
Proposition 3.3.
The following assertions hold.
(1)If  , then for each
, then for each  the tax policy
the tax policy  is a majority winner (a Condorcet winner).
is a majority winner (a Condorcet winner).
(2)If  , then for each
, then for each  the tax policy
the tax policy  is a majority winner (a Condorcet winner).
is a majority winner (a Condorcet winner).
(3)If  and
and  , then the tax policy
, then the tax policy  is a majority winner (a Condorcet winner).
is a majority winner (a Condorcet winner).
Proof of Proposition 3.3.
-
(1)
Let
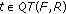 be defined by
be defined by 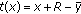 . In order to prove that under the conditions imposed by the hypothesis the function
. In order to prove that under the conditions imposed by the hypothesis the function 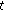 is a majority winner, it is sufficient to show there is no objection to it. Suppose by contrary that there exists
is a majority winner, it is sufficient to show there is no objection to it. Suppose by contrary that there exists 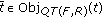 . Then
. Then 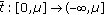 ,
, 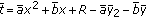 satisfies the feasibility conditions (FA).
satisfies the feasibility conditions (FA).
Figure 2 presents the feasibility areas for the coefficients  and
and  of the functions
of the functions  , which occur in the proofs of the Propositions 3.3 and 3.4. The feasibility areas are determined in a similar way as for the
, which occur in the proofs of the Propositions 3.3 and 3.4. The feasibility areas are determined in a similar way as for the  -feasible taxes: a parallelogram is separated by the line generated by the budget constraint condition.
-feasible taxes: a parallelogram is separated by the line generated by the budget constraint condition.
We denote by  ,
,  , where by
, where by  and
and  we mean
we mean  and
and  , respectively. From the feasibility conditions (FA) for the tax function
, respectively. From the feasibility conditions (FA) for the tax function  , we obtain that the coefficients
, we obtain that the coefficients  and
and  must satisfy
must satisfy  ,
,  , and
, and  . The feasible area for the coefficients
. The feasible area for the coefficients  and
and  can be represented as it is shown in the Figure 2(a).
can be represented as it is shown in the Figure 2(a).
If  , then
, then  and
and  since
since  .
.
If  and
and  , then
, then  and the roots of
and the roots of  satisfy the inequalities
satisfy the inequalities  and
and  (see Lemma 3.1). In this case
(see Lemma 3.1). In this case  (see Table 2, line 2).
(see Table 2, line 2).
If  and
and  , then
, then  and the roots of
and the roots of  satisfy the inequalities
satisfy the inequalities  and
and  (see Lemma 3.1). In this case
(see Lemma 3.1). In this case  (see Table 2, line 3).
(see Table 2, line 3).
So, for any pair  which satisfy the feasibility conditions, the function
which satisfy the feasibility conditions, the function  cannot be an objection to the tax function
cannot be an objection to the tax function  and the tax function
and the tax function  is a majority winner.
is a majority winner.
-
(2)
We will prove that there is no objection to the tax policy
 given by
given by  . Suppose, by contrary that there exists
. Suppose, by contrary that there exists  . Let
. Let 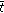 be the tax policy given by
be the tax policy given by 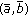 and let
and let  ,
, 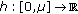 ,
, 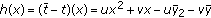 where by
where by  and
and  we mean
we mean 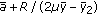 and
and  , respectively. The feasibility conditions for
, respectively. The feasibility conditions for  conduct to the following conditions on the coefficients
conduct to the following conditions on the coefficients  and
and  :
: 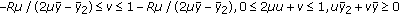 . The feasible area for the coefficients
. The feasible area for the coefficients  and
and  can be represented as it is shown in the Figure 2(b).
can be represented as it is shown in the Figure 2(b).
If  , then
, then  and
and  .
.
If  , then
, then  and the roots of
and the roots of  satisfy the inequalities
satisfy the inequalities  and
and  . In this case
. In this case  (see Table 2, line 4).
(see Table 2, line 4).
If  then
then  and the roots of
and the roots of  satisfy the inequalities
satisfy the inequalities  and
and  . In this case
. In this case  (see Table 2, line 5).
(see Table 2, line 5).
So, for any pair  which belongs to the feasible area, the function
which belongs to the feasible area, the function  cannot be an objection to the tax function
cannot be an objection to the tax function  and the tax policy
and the tax policy  is a Condorcet winner.
is a Condorcet winner.
-
(3)
We will prove that in this case there is no objection to the tax policy
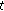 given by
given by 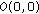 . Suppose by contrary that there exists
. Suppose by contrary that there exists  . Let
. Let 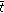 be the tax policy given by
be the tax policy given by 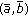 . The feasibility area for the coefficients
. The feasibility area for the coefficients 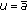 and
and 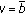 is presented in Figure 2(c).
is presented in Figure 2(c).
If  , then
, then  and
and  .
.
If  , then
, then  ,
,  ,
,  and
and  (see Table 2, line 6).
(see Table 2, line 6).
If  , then
, then  ,
,  ,
,  and
and  (see Table 2, line 5).
(see Table 2, line 5).
In conclusion for any  and
and  such that the pair
such that the pair  belongs to the feasible area, the function
belongs to the feasible area, the function  is not an objection to the tax function
is not an objection to the tax function  . This completes the proof.
. This completes the proof.
 .
.Note that if  , the result from Proposition 3.3(1) was first obtained by De Donder and Hindriks [3] (see Proposition 1(a) in that paper). Proposition 3.3(1) is a generalization: it states that for every feasible value of
, the result from Proposition 3.3(1) was first obtained by De Donder and Hindriks [3] (see Proposition 1(a) in that paper). Proposition 3.3(1) is a generalization: it states that for every feasible value of  , if a majority of individuals is in the low income group, then the voting outcome will determine that all individuals are equal in the posttax income. The second and third parts of the proposition have no empirical relevance since there is overwhelming evidence ruling out negatively skewed income distributions. However, these parts are reported for the purpose of completeness, such that Proposition 3.3 and the next three form together a knit result. (In fact, the results from the last two parts of Proposition 3.3 are very logical; e.g., the second part states that an existing majority of individuals in the upper part of the high income class will induce as a voting outcome the regressive tax system preferred by all the individuals with income in that subclass.)
, if a majority of individuals is in the low income group, then the voting outcome will determine that all individuals are equal in the posttax income. The second and third parts of the proposition have no empirical relevance since there is overwhelming evidence ruling out negatively skewed income distributions. However, these parts are reported for the purpose of completeness, such that Proposition 3.3 and the next three form together a knit result. (In fact, the results from the last two parts of Proposition 3.3 are very logical; e.g., the second part states that an existing majority of individuals in the upper part of the high income class will induce as a voting outcome the regressive tax system preferred by all the individuals with income in that subclass.)
The next two propositions are central for the current paper. We start with the second proposition, that provides a necessary condition for a majority winning tax to exist.
Proposition 3.4.
Let  be such that
be such that  .
.
(1)If  , then for each
, then for each  the tax policy
the tax policy  is a majority winner (a Condorcet winner).
is a majority winner (a Condorcet winner).
(2)If  , then for each
, then for each  the tax policy
the tax policy  is a majority winner (a Condorcet winner).
is a majority winner (a Condorcet winner).
(3)If  , then for each
, then for each  the tax policy
the tax policy  is a majority winner (a Condorcet winner).
is a majority winner (a Condorcet winner).
Proof of Proposition 3.4.
-
(1)
We have to prove that there is no objection to the tax policy
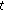 given by
given by 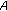 . Let
. Let  be a tax policy given by
be a tax policy given by 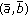 and let
and let 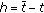 ,
, 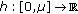 ,
,  , where
, where 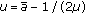 and
and 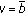 . The feasibility conditions for
. The feasibility conditions for 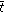 determine the following inequalities:
determine the following inequalities: 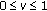 ,
, 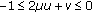 , and
, and 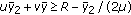 . The feasible area for the coefficients
. The feasible area for the coefficients  and
and  can be represented as it is shown in the Figure 2(d).
can be represented as it is shown in the Figure 2(d).
If  , then
, then  and
and  , which is not an objection to the tax function
, which is not an objection to the tax function  .
.
If  , then
, then  . If
. If  , then
, then  ,
,  and
and  (see Table 2, line 7). If
(see Table 2, line 7). If  , then
, then  ,
,  and
and 
 (see Table 2, line 8). If
(see Table 2, line 8). If  , then
, then  ,
,  and
and  (see Table 2, line 9).
(see Table 2, line 9).
In conclusion, for any pair  which belongs to the feasible area, the function
which belongs to the feasible area, the function  cannot be an objection to the tax function
cannot be an objection to the tax function  . Hence, the tax policy given by
. Hence, the tax policy given by  is a Condorcet winner.
is a Condorcet winner.
-
(2)
We have to prove that there is no objection to the tax policy given by
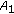 . Let
. Let  be a tax policy given by
be a tax policy given by  , and let
, and let 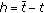 ,
, 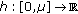 ,
, 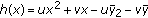 , where
, where 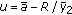 and
and 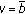 . The feasibility conditions for
. The feasibility conditions for  determine the following inequalities:
determine the following inequalities:  ,
, 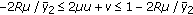 , and
, and 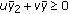 . The feasible area for the coefficients
. The feasible area for the coefficients  and
and  can be represented as it is shown in Figure 2(e).
can be represented as it is shown in Figure 2(e).
If  , then
, then  and
and  .
.
If  , then
, then  and the proof is similar to the correspondent case of the 1st part.
and the proof is similar to the correspondent case of the 1st part.
If  , then
, then  , and after splitting in subcases
, and after splitting in subcases  ,
,  , and
, and  the proofs are similar to the correspondent cases of the 1st part.
the proofs are similar to the correspondent cases of the 1st part.
Hence, the tax policy  is a majority winner.
is a majority winner.
-
(3)
We have to prove that there is no objection to the tax policy
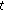 given by
given by 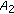 . If
. If 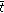 is given by
is given by 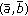 and
and 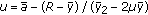 and
and 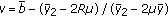 , then the feasibility area for
, then the feasibility area for 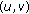 is given by the conditions:
is given by the conditions: 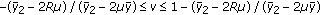 ,
,  , and
, and 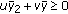 . The feasible area for the coefficients
. The feasible area for the coefficients  and
and  can be represented as it is shown in the Figure 2(f).
can be represented as it is shown in the Figure 2(f).
In this case  and
and  . After splitting in subcases
. After splitting in subcases  and
and  , then the proofs are similar to the correspondent parts of the 1st case.
, then the proofs are similar to the correspondent parts of the 1st case.
Hence, the tax policy  is a majority winner. This completes the proof.
is a majority winner. This completes the proof.
If  , the result from Proposition 3.4(1) was first established by De Donder and Hindriks [3] (see Proposition 1(b) in that paper). However, their result was obtained by imposing the more restrictive condition
, the result from Proposition 3.4(1) was first established by De Donder and Hindriks [3] (see Proposition 1(b) in that paper). However, their result was obtained by imposing the more restrictive condition  . In other words, for every distribution function
. In other words, for every distribution function  such that
such that  , we have with certainty that the maximum progressivity tax is the voting outcome, as far as the median voter prefers this policy. This result does not depend on whether the tax is purely redistributive or not. For purely redistributive taxes, a specific proof is provided in Curt, Litan and Filip [16].
, we have with certainty that the maximum progressivity tax is the voting outcome, as far as the median voter prefers this policy. This result does not depend on whether the tax is purely redistributive or not. For purely redistributive taxes, a specific proof is provided in Curt, Litan and Filip [16].
Therefore, it is enough to have a majority formed by individuals between the upper part of the low income group and the lower part of the high income group, in order to obtain support for the highest tax progressivity. Our next example proves that the necessary condition in Proposition 1(b) in De Donder and Hindriks [3] is overrestrictive. We construct a function  with
with  , in which case the conclusions of our Proposition 3.4 trivially apply.
, in which case the conclusions of our Proposition 3.4 trivially apply.
Example 3.5.
Let  be the distribution function given by
be the distribution function given by

The mean income  , greater than the median income
, greater than the median income  which is equal to
which is equal to  . Routine calculations show that
. Routine calculations show that  ,
,  ,
,  ,
,  ,
,  ,
,  and
and  .
.
For this income distribution, our Proposition 3.4 directly applies (while there is no need to check the necessary and sufficient condition of Proposition 3 in De Donder and Hindriks [3]).
The first and third parts of the Proposition 3.4 advocate the idea that the majority winning tax is the most progressive one, when the median voter is part of the middle income group. Regarding the intuition of the result, straightforward and not surprising is the case in which there is a majority within the middle income group (i.e.,  ); hence, the middle class can afford to minimize its tax, and the burden remains on the rich and the poor.
); hence, the middle class can afford to minimize its tax, and the burden remains on the rich and the poor.
Not intuitively straightforward is the case in which the middle income group cannot form a majority coalition, but there exists a majority formed by individuals between the upper part of the low income group and the lower part of the high income group (i.e.,  ). The policy preferred by the middle income group remains the only majority winner because there is disagreement within the low income group, between the upper part and the rest of the group, and within the high income group, between the lower part and the rest, respectively. Although the second part of the proposition implies a left skewed distribution of the income (not existent in practice), the result is in the same line with the first and third parts: as far as the median voter prefers the tax
). The policy preferred by the middle income group remains the only majority winner because there is disagreement within the low income group, between the upper part and the rest of the group, and within the high income group, between the lower part and the rest, respectively. Although the second part of the proposition implies a left skewed distribution of the income (not existent in practice), the result is in the same line with the first and third parts: as far as the median voter prefers the tax  (together with all the individuals in the subclass to which the median voter belongs), then the majority winner must consist of that policy.
(together with all the individuals in the subclass to which the median voter belongs), then the majority winner must consist of that policy.
The next proposition characterizes the class of income distributions for which the model does not provide a Condorcet winner.
Proposition 3.6.
Let  be such that
be such that  .
.
(1)Let  . If there is
. If there is  such that
such that  , then for each
, then for each  there is no majority winner (Condorcet winner).
there is no majority winner (Condorcet winner).
-
(2)
If
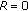 ,
, 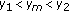 and
and 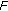 satisfies the previous conditions (in Proposition 3.6(1)), then there is no majority winner (Condorcet winner).
satisfies the previous conditions (in Proposition 3.6(1)), then there is no majority winner (Condorcet winner).
Proof of Proposition 3.6.
In order to prove the result, it is sufficient for each tax policy  to find another tax policy
to find another tax policy  that is an objection to the tax
that is an objection to the tax  , that is,
, that is,  . Let
. Let  be a given tax policy. In our attempt to determine an objection to the tax policy
be a given tax policy. In our attempt to determine an objection to the tax policy  , we are looking for a pair
, we are looking for a pair  such that
such that  ,
,  and
and  . If we denote by
. If we denote by  , then
, then  and
and  . Since the tax policy defined by
. Since the tax policy defined by  must satisfy the feasibility conditions (FA), we have to choose
must satisfy the feasibility conditions (FA), we have to choose  such that
such that  ,
,  ,
,  . Due to the fact that
. Due to the fact that  , we have the following inequalities:
, we have the following inequalities:  and
and  . So, only if
. So, only if  and
and  , there exists
, there exists  such that the previous conditions are satisfied. Since
such that the previous conditions are satisfied. Since  , by applying Lemma 3.1, we obtain:
, by applying Lemma 3.1, we obtain:  and in conclusion
and in conclusion  is an objection for
is an objection for  .
.
It remains to analyze the cases  and
and  . Let
. Let  be a tax policy defined by
be a tax policy defined by  . In order to determine an objection
. In order to determine an objection  , we look for values
, we look for values  ,
,  which satisfy the feasibility conditions (FA) and
which satisfy the feasibility conditions (FA) and  . Since
. Since  , then
, then  and in consequence
and in consequence  . If we denote
. If we denote  , then
, then  and
and  . After short computations, we observe that we must determine
. After short computations, we observe that we must determine  such that
such that  and
and  . In the case when
. In the case when  , then we can choose
, then we can choose  which satisfies the previous restrictions. The policy tax
which satisfies the previous restrictions. The policy tax  is an objection to
is an objection to  due to the fact that
due to the fact that  . In the case when
. In the case when  , then the objection tax policy can be determined in a similar manner by choosing
, then the objection tax policy can be determined in a similar manner by choosing  ,
,  such that
such that  . In the case when
. In the case when  , the objection function
, the objection function  can be also obtained by choosing
can be also obtained by choosing  and
and  which satisfy the feasibility conditions and the equality
which satisfy the feasibility conditions and the equality  . If we denote
. If we denote  , then
, then  and
and  . After short computations, we observe that we must determine
. After short computations, we observe that we must determine  such that
such that  and
and  . In the case when
. In the case when  , then we can choose
, then we can choose  which satisfies the previous restrictions and we get
which satisfies the previous restrictions and we get  . Hence,
. Hence,  is an objection to the tax policy
is an objection to the tax policy  . If
. If  , then
, then  and in consequence
and in consequence  . For
. For  , we have to study the case
, we have to study the case  . In this case the tax policy
. In this case the tax policy  given by
given by  is an objection to
is an objection to  . This completes the proof.
. This completes the proof.
The next proposition specifies what are the conditions for a majority winner to exist and such that the conclusions of Proposition 3.4 remain valid, even if there cannot be formed a majority by individuals between the upper part of the low income group and the lower part of the high income group.
Proposition 3.7.
Let  and
and  . If for each
. If for each  we have
we have  , then the conclusions of the Proposition 3.4 are true.
, then the conclusions of the Proposition 3.4 are true.
Proof of Proposition 3.7.
Similar to the proof of the Proposition 3.4.
The intuition of this proposition is not straightforward and resides in the same type of arguments invoked by De Donder and Hindriks [3]. The maximum progressivity has majority support due to the disagreement, not only between the lower and upper parts of the high income group, but also among the individuals of the upper part of this income class. Analogous analysis can be performed for the low income class.
To be more specific, for any tax change (represented by the parameter  ) involving less progressivity (parameter
) involving less progressivity (parameter  ) and higher flat tax parameter (
) and higher flat tax parameter ( ), there is always some poor with income higher than
), there is always some poor with income higher than  who do not find the increase in
who do not find the increase in  large enough to compensate for the lower
large enough to compensate for the lower  . As well, there is always some rich with income lower than
. As well, there is always some rich with income lower than  who do not find the decrease in
who do not find the decrease in  large enough to compensate for the increase in
large enough to compensate for the increase in  . The group in disagreement with the extremes for a given tax change is larger now than in Proposition 3.4, that is,
. The group in disagreement with the extremes for a given tax change is larger now than in Proposition 3.4, that is,  . Therefore the condition on the distribution of income in Proposition 3.7 ensures that the size of the group
. Therefore the condition on the distribution of income in Proposition 3.7 ensures that the size of the group  is large enough to form a majority, for any possible
is large enough to form a majority, for any possible  .
.
4. Conclusions
We identified what are the most preferred taxes of the individuals (and the corresponding income groups they can be classified in, based on the preferred policies), for every case of taxation that has more than a purely redistributive purpose (meaning that the tax should collect some positive amount  ). In particular, we have proved that if the model departs from the purely redistributive feature, then, at least within the high income class, the preferences differ between the groups
). In particular, we have proved that if the model departs from the purely redistributive feature, then, at least within the high income class, the preferences differ between the groups  and
and  . This fact is essential to understand the result which states that the sufficient condition of De Donder and Hindriks [3] can be relaxed to a broader one.
. This fact is essential to understand the result which states that the sufficient condition of De Donder and Hindriks [3] can be relaxed to a broader one.
Indeed, for not very large collected amounts  , it is enough to have a majority formed by individuals between the upper part of the low income group and the lower part of the high income group, in order to insure support for the highest tax progressivity (as far as the median voter prefers this policy, that is,
, it is enough to have a majority formed by individuals between the upper part of the low income group and the lower part of the high income group, in order to insure support for the highest tax progressivity (as far as the median voter prefers this policy, that is,  ). For
). For  , the results in De Donder and Hindriks [3] were obtained around the more restrictive condition
, the results in De Donder and Hindriks [3] were obtained around the more restrictive condition  . However, the case of purely redistributive taxations can be seen as a limiting case of those situations in which the taxes should collect some positive amounts. Therefore, for
. However, the case of purely redistributive taxations can be seen as a limiting case of those situations in which the taxes should collect some positive amounts. Therefore, for  and for every distribution function
and for every distribution function  such that
such that  , it is also certain that the maximum progressivity is the voting outcome. Example 3.5 shows that the set of the distribution functions with the above property is not empty.
, it is also certain that the maximum progressivity is the voting outcome. Example 3.5 shows that the set of the distribution functions with the above property is not empty.
For reasons of completeness, the paper provides an overall description of those income distribution functions for which a majority winning tax exists (or does not exist), when the quadratic taxation model is not purely redistributive. For the same reasons of completeness, the analysis considers both the right skewed income distributions, which are predominant in practice, but also the left skewed ones are analyzed (see the second and third parts of Proposition 3.3, and the second part of Proposition 3.4). We conclude with the idea that, should any political equilibrium different than the Condorcet winner be proposed, it is important to be first tested on those quadratic taxation models without majority winners (both for purely, as well as for nonpurely redistributive taxations). Our work offers a complete mathematical description of this testing set of models.
References
Marhuenda F, Ortuño-Ortín I: Income taxation, uncertainty and stability. Journal of Public Economics 1998, 67(2):285–300. 10.1016/S0047-2727(97)00054-6
Hindriks J: Is there a demand for income tax progressivity? Economics Letters 2001, 73(1):43–50. 10.1016/S0165-1765(01)00459-1
De Donder P, Hindriks J: Majority support for progressive income taxation with corner preferences. Public Choice 2004, 118(3–4):437–449.
Romer T: Individual welfare, majority voting, and the properties of a linear income tax. Journal of Public Economics 1975, 4(2):163–185. 10.1016/0047-2727(75)90016-X
Romer T: Majority voting on tax parameters. Journal of Public Economics 1977, 7(1):127–133. 10.1016/0047-2727(77)90040-8
Roberts KWS: Voting over income tax schedules. Journal of Public Economics 1977, 8(3):329–340. 10.1016/0047-2727(77)90005-6
Gouveia M, Oliver D: Voting over flat taxes in an endowment economy. Economics Letters 1996, 50(2):251–258. 10.1016/0165-1765(95)00749-0
Cukierman A, Meltzer H: A political theory of income taxation. In Political Economy. Edited by: Meltzer A, Cukierman A, Richards F. Oxford University Press, Oxford, UK; 1991:78–106.
Roemer JE: The democratic political economy of progressive income taxation. Econometrica 1999, 67(1):1–19. 10.1111/1468-0262.00001
Carbonell-Nicolau O, Klor EF: Representative democracy and marginal rate progressive income taxation. Journal of Public Economics 2003, 87(5–6):1137–1164. 10.1016/S0047-2727(01)00138-4
Marhuenda F, Ortuño-Ortín I: Popular support for progressive taxation. Economics Letters 1995, 48(3–4):319–324. 10.1016/0165-1765(95)94399-G
Carbonell-Nicolau O, Ok EA: Voting over income taxation. Journal of Economic Theory 2007, 134(1):249–286. 10.1016/j.jet.2006.02.008
Klor F: On the popular support for progressive taxation. Journal of Public Economic Theory 2003, 5: 593–604. 10.1111/1467-9779.t01-1-00150
De Donder P, Hindriks J: The politics of progressive income taxation with incentive effects. Journal of Public Economics 2003, 87(11):2491–2505. 10.1016/S0047-2727(02)00051-8
Grandmont M: Fiscally stable distributions under majority voting. Advances in Mathematical Economics 2006, 8: 215–230. 10.1007/4-431-30899-7_8
Curt P, Litan CM, Filip A: Comment on the majority support for progressive income taxation with corner preferences. preprint, 2010
Acknowledgments
The authors would like to thank Francisco Marhuenda for helpful comments. Cristian Litan aknowledges preliminary discussions with Luis Corchón. Diana Andrada Filip and Paula Curt acknowledge financial support by CNSIS-UEFISCU, project number PNII-IDEI 2366/2008. Cristian Litan acknowledges financial support by CNCSIS-UEFISCSU, project number PN II-RU 415/2010. The usual disclaimer applies.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Curt, P., Litan, C. & Filip, D. A Mathematical Revisit of Modeling the Majority Voting on Fixed-Income Quadratic Taxations. J Inequal Appl 2010, 329378 (2010). https://doi.org/10.1155/2010/329378
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/329378
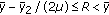 is represented in Figure
is represented in Figure 
 .
.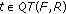 be defined by
be defined by 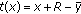 . In order to prove that under the conditions imposed by the hypothesis the function
. In order to prove that under the conditions imposed by the hypothesis the function 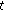 is a majority winner, it is sufficient to show there is no objection to it. Suppose by contrary that there exists
is a majority winner, it is sufficient to show there is no objection to it. Suppose by contrary that there exists 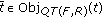 . Then
. Then 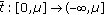 ,
, 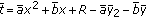 satisfies the feasibility conditions (FA).
satisfies the feasibility conditions (FA). given by
given by  . Suppose, by contrary that there exists
. Suppose, by contrary that there exists  . Let
. Let 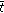 be the tax policy given by
be the tax policy given by 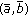 and let
and let  ,
, 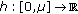 ,
, 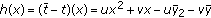 where by
where by  and
and  we mean
we mean 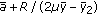 and
and  , respectively. The feasibility conditions for
, respectively. The feasibility conditions for  conduct to the following conditions on the coefficients
conduct to the following conditions on the coefficients  and
and  :
: 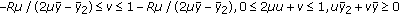 . The feasible area for the coefficients
. The feasible area for the coefficients  and
and  can be represented as it is shown in the Figure
can be represented as it is shown in the Figure  given by
given by 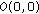 . Suppose by contrary that there exists
. Suppose by contrary that there exists  . Let
. Let 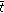 be the tax policy given by
be the tax policy given by 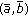 . The feasibility area for the coefficients
. The feasibility area for the coefficients 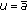 and
and 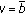 is presented in Figure
is presented in Figure 
 and
and  .
.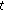 given by
given by 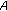 . Let
. Let  be a tax policy given by
be a tax policy given by 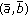 and let
and let 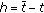 ,
, 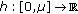 ,
,  , where
, where 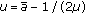 and
and 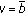 . The feasibility conditions for
. The feasibility conditions for 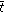 determine the following inequalities:
determine the following inequalities: 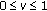 ,
, 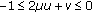 , and
, and 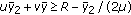 . The feasible area for the coefficients
. The feasible area for the coefficients  and
and  can be represented as it is shown in the Figure
can be represented as it is shown in the Figure 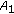 . Let
. Let  be a tax policy given by
be a tax policy given by  , and let
, and let 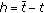 ,
, 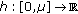 ,
, 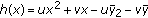 , where
, where 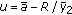 and
and 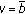 . The feasibility conditions for
. The feasibility conditions for  determine the following inequalities:
determine the following inequalities:  ,
, 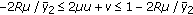 , and
, and 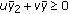 . The feasible area for the coefficients
. The feasible area for the coefficients  and
and  can be represented as it is shown in Figure
can be represented as it is shown in Figure 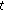 given by
given by 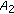 . If
. If 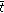 is given by
is given by 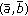 and
and 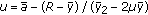 and
and 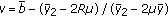 , then the feasibility area for
, then the feasibility area for 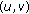 is given by the conditions:
is given by the conditions: 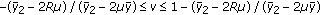 ,
,  , and
, and 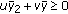 . The feasible area for the coefficients
. The feasible area for the coefficients  and
and  can be represented as it is shown in the Figure
can be represented as it is shown in the Figure 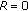 ,
, 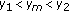 and
and 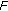 satisfies the previous conditions (in Proposition 3.6(1)), then there is no majority winner (Condorcet winner).
satisfies the previous conditions (in Proposition 3.6(1)), then there is no majority winner (Condorcet winner).