- Research Article
- Open access
- Published:
On a Multiple Hilbert's Inequality with Parameters
Journal of Inequalities and Applications volume 2010, Article number: 309319 (2010)
Abstract
By introducing multiparameters and conjugate exponents and using Hadamard's inequality and the way of real analysis, we estimate the weight coefficients and give a multiple more accurate Hilbert's inequality, which is an extension of some published results. We also prove that the constant factor in the new inequality is the best possible and consider its equivalent form.
1. Introduction
In 1908, Weyl published the following famous Hilbert's inequality (cf. [1]). If  ,
, and
and  then
then

where the constant factor is the best possible. In 1934, Hardy proved the following more accurate Hilbert's inequality (cf. [2]):
is the best possible. In 1934, Hardy proved the following more accurate Hilbert's inequality (cf. [2]):

where the constant factor is the best possible. For
is the best possible. For  the equivalent forms of (1.1) and (1.2) are given as follows (cf. [2]):
the equivalent forms of (1.1) and (1.2) are given as follows (cf. [2]):


where the constant factor is the best possible. Inequalities (1.1)–(1.4) are important in analysis and their applications (cf. [3]). In near one century, there are many improvements, generalizations and, applications of (1.1)–(1.4) in numerous literatures and monographs of mathematics (cf. [2–18]). Yang and Huang also considered the multiple Hilbert-type integral inequality (cf. [19, 20]). Recently, Yang summarized the methods of introducing parameters and estimating the weight coefficients to extend Hilbert-type inequalities for the past 100 years. Some representative results are as follows (cf. [21, 22]):
is the best possible. Inequalities (1.1)–(1.4) are important in analysis and their applications (cf. [3]). In near one century, there are many improvements, generalizations and, applications of (1.1)–(1.4) in numerous literatures and monographs of mathematics (cf. [2–18]). Yang and Huang also considered the multiple Hilbert-type integral inequality (cf. [19, 20]). Recently, Yang summarized the methods of introducing parameters and estimating the weight coefficients to extend Hilbert-type inequalities for the past 100 years. Some representative results are as follows (cf. [21, 22]):
(i)if  ,
,  ,
,  then
then




-
(ii)
if
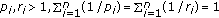 ,
,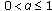 ,
, , then
, then

The constant factors in the above five inequalities are all the best possible. Inequalities (1.5) and (1.7) are generalizations of inequality (1.2), and inequality (1.9) is a multiple extension of (1.1). Inequalities (1.6) and (1.8) are the equivalent forms of (1.5) and (1.7), which are extensions of (1.4).
In this paper, by introducing multi-parameters and conjugate exponents and using Hadamard's inequality, we estimate the weight coefficients and give a multiple more accurate Hilbert 's inequality, which is an extension of inequalities (1.5), (1.7), and (1.9). We also prove that the constant factor in the new inequality is the best possible and consider its equivalent form.
2. Some Lemmas
Lemma 2.1.
If  ,
,  ,
,  ,
,  ,
,  , then
, then

Proof.
We find the following:

and then (2.1) is valid.
Lemma 2.2.
If  ,
, ,
,  ,
, ,
, ,
, then
then

Proof.
For fixed we set
we set

In virtue of  and
and  we find
we find  ,
, Putting
Putting  we have the following:
we have the following:

Since  by the following Hadamard's inequality (cf. [5]):
by the following Hadamard's inequality (cf. [5]):

it follows that

and then we have the right-hand side of (2.3). Since

and  is strictly decreasing in
is strictly decreasing in  , we get
, we get

Hence, we prove that the left-hand side of (2.3) is valid.
Lemma 2.3.
As the assumption of Lemma 2.1, define the weight coefficients  as
as


, then there exists  such that
such that

Moreover, for any  it follows that
it follows that

Proof.
We prove (2.11) by mathematical induction. For  we set
we set  and
and  satisfying
satisfying  Putting
Putting  ,
, ,
, we have the following:
we have the following:

and then (2.11) is valid by using inequality (2.3).
Assuming that for  (2.11) is valid, then for
(2.11) is valid, then for  setting
setting  ,
,  by (2.3), we have the following:
by (2.3), we have the following:

Setting  ,
,  ,
,  we find
we find  ,
,  By the assumption of induction, it follows that
By the assumption of induction, it follows that


where  and
and

Setting  by (2.16), we have the following:
by (2.16), we have the following:

and then by (2.15), (2.18), and mathematical induction, (2.11) is valid. Setting  ,
, ,
, ,
, ,
, ,
,  then we have the following:
then we have the following:

Hence, (2.12) is valid.
3. Main Results
Theorem 3.1.
Suppose that  ,
, ,
,  ,
, ,
,  ,
,  ,
,  ,
,  ,
, 
 such that
such that

then one has the following equivalent inequalities:


Proof.
Since  by (2.1) and Hölder's inequality (cf. [5]), we find that
by (2.1) and Hölder's inequality (cf. [5]), we find that


For  since
since by Hölder's inequality again in (3.5), we have the following:
by Hölder's inequality again in (3.5), we have the following:

Note that for  by (3.5), we directly get (3.6). Hence, (3.3) is valid by (3.6) and (2.12).
by (3.5), we directly get (3.6). Hence, (3.3) is valid by (3.6) and (2.12).
Since  by Hölder's inequality once again, it follows that
by Hölder's inequality once again, it follows that

By (3.3), we have (3.2). On the other hand, assuming that (3.2) is valid, setting

then we find that

By (3.2), it follows that  If
If  then (3.3) is naturally valid. Suppose that
then (3.3) is naturally valid. Suppose that  by (3.2), we find that
by (3.2), we find that

Dividing out  into two sides of (3.10), we have the following:
into two sides of (3.10), we have the following:

Then (3.3) is valid, which is equivalent to (3.2).
Theorem 3.2.
Let the assumptions of Theorem 3.1 be fulfilled, then the same constant factor  in (3.2) and (3.3) is the best possible.
in (3.2) and (3.3) is the best possible.
Proof.
By (2.11) and

there exists  such that for
such that for  ,
,

where  Setting
Setting

we find that

If there exists a constant  such that (3.2) is still valid as we replace
such that (3.2) is still valid as we replace  by
by  then in particular, we have the following:
then in particular, we have the following:

In virtue of (3.15) and (3.16), it follows that

For  , we have
, we have  Hence,
Hence,  is the best value of (3.2).
is the best value of (3.2).
We conform that the constant factor  in (3.3) is the best possible, otherwise we can get a contradiction by (3.7) that the constant factor in (3.2) is not the best possible.
in (3.3) is the best possible, otherwise we can get a contradiction by (3.7) that the constant factor in (3.2) is not the best possible.
Remarks 3.3 ..
-
(i)
When
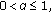 the assumption
the assumption 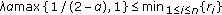 of two theorems becomes
of two theorems becomes  (ii) When
(ii) When 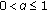 ,
,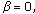 (3.2) reduces to (1.9). (iii) For
(3.2) reduces to (1.9). (iii) For 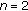 ,
, 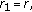
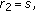
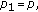
 setting
setting 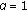 ,
,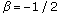 in (3.2), then
in (3.2), then  we obtain (1.5). Setting
we obtain (1.5). Setting  ,
,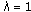 in (3.2), we get (1.7).
in (3.2), we get (1.7).
References
Weyl H: Singulare integral gleichungen mit besonderer berucksichtigung des fourierschen integral theorems, Inaugural-Dissertation. Göttingen University, Göttingen, Germany; 1908.
Hardy GH, Littlewood JE, Pólya G: Inequalities. Cambridge University Press, Cambridge, UK; 1934.
Mitrinović DS, Pečarić JE, Fink AM: Inequalities Involving Functions and Their Integrals and Derivatives. Volume 53. Kluwer Academic, Boston, Mass, USA; 1991:xvi+587.
Zhong W: A Hilbert-type linear operator with the norm and its applications. Journal of Inequalities and Applications 2009, 2009:-18.
Kuang JC: Applied Inequalitie. Shangdong Science Technic Press, Jinan, China; 2004.
Hu K: Some Problems in Analysis Inequalities. Wuhan University Press, Wuhan, China; 2007.
Magnus W: On the spectrum of Hilbert's matrix. American Journal of Mathematics 1950, 72: 699–704. 10.2307/2372284
Yang BC, Gao MZ: On a best value of Hardy-Hilbert's inequality. Advances in Mathematics 1997, 26(2):159–164.
Gao MZ, Yang BC: On the extended Hilbert's inequality. Proceedings of the American Mathematical Society 1998, 126(3):751–759. 10.1090/S0002-9939-98-04444-X
Jichang K: On new extensions of Hilbert's integral inequality. Journal of Mathematical Analysis and Applications 1999, 235(2):608–614. 10.1006/jmaa.1999.6373
Yang BC, Debnath L: On the extended Hardy-Hilbert's inequality. Journal of Mathematical Analysis and Applications 2002, 272(1):187–199. 10.1016/S0022-247X(02)00151-8
Yang BC: An extension of Hardy-Hilbert's inequality. Chinese Annals of Mathematics 2002, 23(2):247–254.
Yang BC, Rassias TM: On a new extension of Hilbert's inequality. Mathematical Inequalities & Applications 2005, 8(4):575–582.
Yang B: On a new extension of Hilbert's inequality with some parameters. Acta Mathematica Hungarica 2005, 108(4):337–350. 10.1007/s10474-005-0229-4
Yang BC: Hilbert's inequality with some parameters. Acta Mathematica Sinica. Chinese Series 2006, 49(5):1121–1126.
Yang BC: A dual Hardy-Hilbert's inequality and generalizations. Advances in Mathematics 2006, 35(1):102–108.
Yang BC: On a Hilbert-type operator with a symmetric homogeneous kernel of --order and applications. Journal of Inequalities and Applications 2007, -9.
Yang BC: On the norm of a linear operator and its applications. Indian Journal of Pure and Applied Mathematics 2008, 39(3):237–250.
Yang BC: Hilbert-type Integral Inequalities. Bentham Science, Oak Park, Ill, USA; 2009.
Huang Q, Yang BC: On a multiple Hilbert-type integral operator and applications. Journal of Inequalities and Applications 2009, 2009:-13.
Yang BC: The Norm of Operator and Hilbert-Type Inequalities. Science Press, Beijing, China; 2009.
Yang BC: A survey of the study of Hilbert-type inequalities with parameters. Advances in Mathematics 2009, 38(3):257–268.
Acknowledgments
This work is supported by the Emphases Natural Science Foundation of Guangdong Institution, Higher Learning, College and University (no. 05Z026), and Guangdong Natural Science Foundation (no. 7004344).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Huang, Q. On a Multiple Hilbert's Inequality with Parameters. J Inequal Appl 2010, 309319 (2010). https://doi.org/10.1155/2010/309319
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/309319
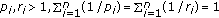 ,
,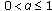 ,
, , then
, then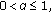 the assumption
the assumption 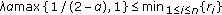 of two theorems becomes
of two theorems becomes  (ii) When
(ii) When 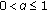 ,
,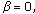 (3.2) reduces to (1.9). (iii) For
(3.2) reduces to (1.9). (iii) For 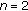 ,
, 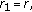
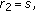
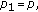
 setting
setting 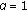 ,
,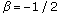 in (3.2), then
in (3.2), then  we obtain (1.5). Setting
we obtain (1.5). Setting  ,
,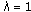 in (3.2), we get (1.7).
in (3.2), we get (1.7).