- Research Article
- Open access
- Published:
Moment Estimation Inequalities Based on  Random Variable on Sugeno Measure Space
Random Variable on Sugeno Measure Space
Journal of Inequalities and Applications volume 2010, Article number: 290124 (2010)
Abstract
The definitions and properties of moment of  random variable are provided on Sugeno measure space. Then some important moment estimation inequalities based on
random variable are provided on Sugeno measure space. Then some important moment estimation inequalities based on  random variable are presented and proven.
random variable are presented and proven.
1. Introduction
In 1974, the Japanese scholar Sugeno [1] presented a kind of typical nonadditive measure, Sugeno measure, which is an important generalization of probability measure [2–6]. As we all know, the definitions and properties of moment of random variable play an important role in probability theory [7–9]. Likewise, they are also very important for Sugeno measure. In this paper we present the analogous definitions and properties based on  random variable on Sugeno measure space. Then some important moment estimation inequalities based on
random variable on Sugeno measure space. Then some important moment estimation inequalities based on  random variable are presented and proven.
random variable are presented and proven.
2. Preliminaries
Let us recall some definitions and facts from [5].
Definition 2.1.
Let  be a nonempty set, let
be a nonempty set, let  be a nonempty class of subsets of
be a nonempty class of subsets of  , and let
, and let  be a nonnegative real valued set function defined on
be a nonnegative real valued set function defined on  . Therefore
. Therefore  satisfies the
satisfies the  -
- rule (on
rule (on  ) if and only if there exists
) if and only if there exists

such that

for any disjoint sequence  of sets in
of sets in  whose union is also in
whose union is also in  .
.
Definition 2.2.
Let  be a
be a  -algebra of subsets of
-algebra of subsets of  . And
. And  is called Sugeno measure on
is called Sugeno measure on  if and only if it satisfies the
if and only if it satisfies the  -
- rule and
rule and  . Usually, Sugeno measure on
. Usually, Sugeno measure on  is denoted by
is denoted by  .
.
We call the triple  a Sugeno measure space, denoted by
a Sugeno measure space, denoted by  space, where
space, where  . In the following, our discussion will be restricted to this space.
. In the following, our discussion will be restricted to this space.
Theorem 2.3.
For all  imply that
imply that  (monotonicity).
(monotonicity).
Theorem 2.4.
Let  be a Sugeno measure on
be a Sugeno measure on  . Then, for any
. Then, for any  and
and  ,
,

In order to present the analogous definitions and properties based on  random variable on Sugeno measure space, we recall some definitions and facts from [10].
random variable on Sugeno measure space, we recall some definitions and facts from [10].
Definition 2.5.
Let  be a function mapping from
be a function mapping from  to real line
to real line  . Then
. Then  is called a
is called a  random variable.
random variable.
Definition 2.6.
Let  be a
be a  random variable. Then the distribution function of
random variable. Then the distribution function of  is defined by
is defined by

Definition 2.7.
Let  be the distribution function of
be the distribution function of  random variable
random variable  . Then
. Then  is called continuous
is called continuous  random variable if there exists a nonnegative real valued function
random variable if there exists a nonnegative real valued function  such that
such that

is valid. The function  is called a density function of
is called a density function of  .
.
In the following, our discussion will be restricted to the continuous  random variable.
random variable.
Definition 2.8.
Let  be the distribution function of
be the distribution function of  random variable
random variable  . If
. If  , then we call
, then we call  an expected value of
an expected value of  random variable
random variable  , denoted by
, denoted by  .
.
Theorem 2.9.
Let  ,
, be
be  random variables; let C and D be constants. Then
random variables; let C and D be constants. Then

Definition 2.10.
Let  be a
be a  random variable. If
random variable. If  exists, then
exists, then  is called the variance of
is called the variance of  , denoted by
, denoted by  .
.
3. Moment Estimation Inequalities Based on 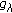 Random Variable
Random Variable
We begin this section with a short lemma (see [11]), which will be useful in the sequel.
Lemma 3.1.
Let  be a
be a  random variable whose Sugeno density function
random variable whose Sugeno density function  exists. If the Lebesgue integral
exists. If the Lebesgue integral

is finite, then

Theorem 3.2.
Let  be a nonnegative
be a nonnegative  random variable. When
random variable. When  , the inequality
, the inequality

is valid; when  , the inequality
, the inequality

holds true.
Proof.
-
(I)
When
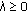 , since
, since 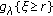 is a monotone decreasing function of
is a monotone decreasing function of 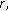 we have
we have 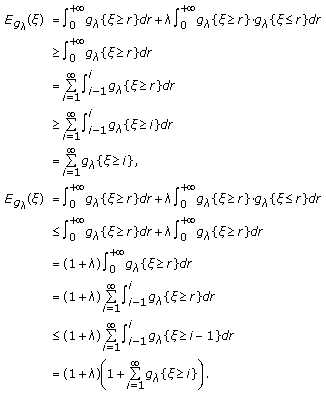 (3.5)
(3.5)
-
(II)
When
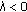 , owing to the monotonicity of
, owing to the monotonicity of 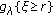 we also have
we also have

Definition 3.3.
Let  be a
be a  random variable and
random variable and  a positive number. Then
a positive number. Then  the expected value
the expected value  is called the
is called the  th moment,
th moment,  the expected value
the expected value  is called the
is called the  th absolute moment,
th absolute moment,  the expected value
the expected value  is called the
is called the  th central moment, and
th central moment, and  the expected value
the expected value  is called the
is called the  th absolute central moment.
th absolute central moment.
Theorem 3.4.
Let  be a nonnegative
be a nonnegative  random variable and
random variable and  a positive number. Then
a positive number. Then

Proof.
From Lemma 3.1, we infer

Similar to the case of credibility theory [12], we have the following: Theorems 3.5, 3.6, and 3.7.
Theorem 3.5.
Let  be a
be a  random variable that takes values in
random variable that takes values in  and has expected value
and has expected value  , and let
, and let  be a convex function on
be a convex function on  . Then
. Then

Theorem 3.6.
Let  be a
be a  random variable that takes values in
random variable that takes values in  and has expected value
and has expected value  . Then
. Then

Theorem 3.7.
Let  be a
be a  random variable that takes values in
random variable that takes values in  and has expected value
and has expected value  . Then, for any positive integer
. Then, for any positive integer  ,
,

Theorem 3.8.
Let  be a
be a  random variable and
random variable and  Then
Then  if and only if
if and only if  .
.
Proof.
From  and Theorem 3.2, the conclusion is valid.
and Theorem 3.2, the conclusion is valid.
Theorem 3.9.
Let  be a
be a  random variable and
random variable and  . If
. If  then
then  Conversely, if there exists one positive number
Conversely, if there exists one positive number  such that
such that  , then
, then  for any
for any  where
where 
Proof.
-
(1)
When
 , we have
, we have 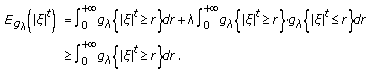 (3.12)
(3.12)
Since  we obtain
we obtain  Consequently,
Consequently,

Since

we have

-
(2)
When
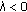 , we have
, we have

Since

we obtain

Consequently,

Since

we have

Conversely, if  then there exists one number
then there exists one number  such that
such that  , for all
, for all 
-
(3)
When
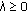 , for any
, for any  where
where 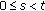 , we have
, we have

Since  for any
for any  we have
we have

-
(4)
When
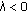 , for any
, for any 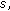 where
where 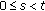 , we have
, we have 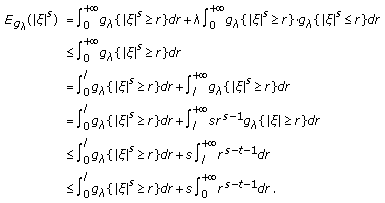 (3.24)
(3.24)
Since  for any
for any  we have
we have

References
Sugeno M: Theory of fuzzy integrals and its applications, Ph.D. dissertation. Tokyo Institute of Technology; 1974.
Basile A: Sequential compactness for sets of Sugeno fuzzy measures. Fuzzy Sets and Systems 1987, 21(2):243–247. 10.1016/0165-0114(87)90168-0
Berres M:
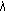 -additive measures on measure spaces. Fuzzy Sets and Systems 1988, 27(2):159–169. 10.1016/0165-0114(88)90146-7
-additive measures on measure spaces. Fuzzy Sets and Systems 1988, 27(2):159–169. 10.1016/0165-0114(88)90146-7Chen T-Y, Wang J-C, Tzeng G-H: Identification of general fuzzy measures by genetic algorithms based on partial information. IEEE Transactions on Systems, Man, and Cybernetics, Part B 2000, 30(4):517–528.
Wang ZY, Klir GJ: Fuzzy Measure Theory. Plenum Press, New York, NY, USA; 1992:x+354.
Wierzchon ST: An algorithm for identification of fuzzy measure. Fuzzy Sets and Systems 1983, 9(1):69–78. 10.1016/S0165-0114(83)80005-0
Graversen SE, Peškir G: Maximal inequalities for Bessel processes. Journal of Inequalities and Applications 1998, 2(2):99–119. 10.1155/S102558349800006X
Sung SH: Moment inequalities and complete moment convergence. Journal of Inequalities and Applications 2009, 2009:-14.
Zang Q-P: A limit theorem for the moment of self-normalized sums. Journal of Inequalities and Applications 2009, 2009:-10.
Ha M, Li Y, Li J, Tian D: The key theorem and the bounds on the rate of uniform convergence of learning theory on Sugeno measure space. Science in China. Series F 2006, 49(3):372–385. 10.1007/s11432-006-0372-8
Ha M, Zhang H, Pedrycz W, Xing H: The expected value models on Sugeno measure space. International Journal of Approximate Reasoning 2009, 50(7):1022–1035. 10.1016/j.ijar.2009.03.008
Liu B: Uncertainty Theory. An Introduction to Its Axiomatic Foundation, Studies in Fuzziness and Soft Computing. Volume 154. Springer; Plenum, Berlin, Germany; 2004:xii+411.
Acknowledgment
This work was supported by the NNSF of China (no. 60773062), the NSF of Hebei Province of China (no. 2008000633), the foundation of North China Electric Power University (no. 200911033), the KSRP of Department of Education of Hebei Province of China (no. 2005001D), and the KSTRP of Ministry of Education of China (no. 206012).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Tian, J., Zhang, Z. & Tian, D. Moment Estimation Inequalities Based on  Random Variable on Sugeno Measure Space.
J Inequal Appl 2010, 290124 (2010). https://doi.org/10.1155/2010/290124
Random Variable on Sugeno Measure Space.
J Inequal Appl 2010, 290124 (2010). https://doi.org/10.1155/2010/290124
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/290124
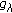 Random Variable
Random Variable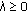 , since
, since 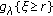 is a monotone decreasing function of
is a monotone decreasing function of 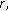 we have
we have 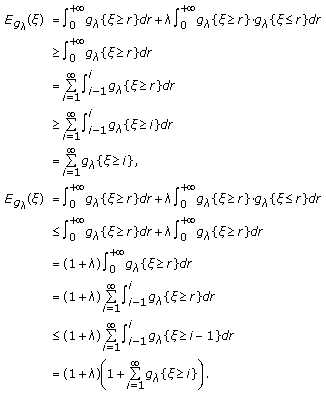
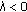 , owing to the monotonicity of
, owing to the monotonicity of 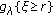 we also have
we also have , we have
, we have 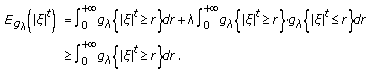
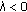 , we have
, we have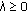 , for any
, for any  where
where 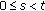 , we have
, we have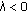 , for any
, for any 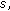 where
where 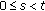 , we have
, we have 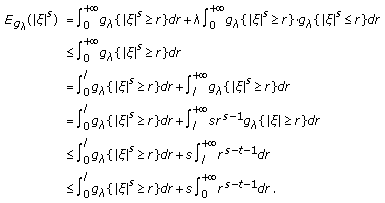
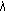 -additive measures on measure spaces. Fuzzy Sets and Systems 1988, 27(2):159–169. 10.1016/0165-0114(88)90146-7
-additive measures on measure spaces. Fuzzy Sets and Systems 1988, 27(2):159–169. 10.1016/0165-0114(88)90146-7