- Research Article
- Open access
- Published:
A New Iteration Method for Nonexpansive Mappings and Monotone Mappings in Hilbert Spaces
Journal of Inequalities and Applications volume 2010, Article number: 251761 (2010)
Abstract
We introduce a new composite iterative scheme by the viscosity approximation method for nonexpansive mappings and monotone mappings in a Hilbert space. It is proved that the sequence generated by the iterative scheme converges strongly to a common point of set of fixed points of nonexpansive mapping and the set of solutions of variational inequality for an inverse-strongly monotone mappings, which is a solution of a certain variational inequality. Our results substantially develop and improve the corresponding results of [Chen et al. 2007 and Iiduka and Takahashi 2005]. Essentially a new approach for finding the fixed points of nonexpansive mappings and solutions of variational inequalities for monotone mappings is provided.
1. Introduction
Let  be a real Hilbert space and
be a real Hilbert space and  a nonempty closed convex subset of
a nonempty closed convex subset of  . Recall that a mapping
. Recall that a mapping  is a contraction on
is a contraction on  if there exists a constant
if there exists a constant  such that
such that  We use
We use  to denote the collection of mappings
to denote the collection of mappings  verifying the above inequality. That is
verifying the above inequality. That is  . A mapping
. A mapping  is called nonexpansive if
is called nonexpansive if  ; see [1, 2] for the results of nonexpansive mappings. We denote by
; see [1, 2] for the results of nonexpansive mappings. We denote by  the set of fixed points of
the set of fixed points of  ; that is,
; that is, 
Let  be the metric projection of
be the metric projection of  onto
onto  . A mapping
. A mapping  of
of  into
into  is called monotone if for
is called monotone if for  ,
,  . The variational inequality problem is to find a
. The variational inequality problem is to find a  such that
such that

for all  ; see [3–6]. The set of solutions of the variational inequality is denoted by
; see [3–6]. The set of solutions of the variational inequality is denoted by  . A mapping
. A mapping  of
of  into
into  is called inverse-strongly monotone if there exists a positive real number
is called inverse-strongly monotone if there exists a positive real number  such that
such that

for all  ; see [7–9]. For such a case,
; see [7–9]. For such a case,  is called
is called  -inverse-strongly monotone.
-inverse-strongly monotone.
In 2005, Iiduka and Takahashi [10] introduced an iterative scheme for finding a common point of the set of fixed points of a nonexapnsive mapping and the set of solutions of the variational inequality for an inverse-strong monotone mapping as follows. For an  -inverse-strongly monotone mapping
-inverse-strongly monotone mapping  of
of  to
to  and a nonexpansive mapping
and a nonexpansive mapping  of
of  into itself such that
into itself such that  ,
,  ,
,  , and
, and  ,
,

for every  . They proved that the sequence generated by (1.3) converges strongly to
. They proved that the sequence generated by (1.3) converges strongly to  under the conditions on
under the conditions on  and
and  for some
for some  with
with  ,
,

On the other hand, the viscosity approximation method of selecting a particular fixed point of a given nonexpansive mapping was proposed by Moudafi [11]. In 2004, in order to extend Theorem 2.2 of Moudafi [11] to a Banach space setting, Xu [12] considered the the following explicit iterative process. For  nonexpansive mappings,
nonexpansive mappings,  and
and  ,
,

Moreover, in [12], he also studied the strong convergence of  generated by (1.5) as
generated by (1.5) as  in either a Hilbert space or a uniformly smooth Banach space and showed that the strong
in either a Hilbert space or a uniformly smooth Banach space and showed that the strong  is a solution of a certain variational inequality.
is a solution of a certain variational inequality.
In 2007, Chen et al. [13] considered the following iterative scheme as the viscosity approximation method of (1.3). For an  -inverse-strongly-monotone mapping
-inverse-strongly-monotone mapping  of
of  to
to  and a nonexpansive mapping
and a nonexpansive mapping  of
of  into itself such that
into itself such that  ,
,  ,
,  ,
,  , and
, and  ,
,

and showed that the sequence  generated by (1.6) converges strongly to a point in
generated by (1.6) converges strongly to a point in  under condition (1.4) on
under condition (1.4) on  and
and  , which is a solution of a certain variational inequality.
, which is a solution of a certain variational inequality.
In this paper, motivated by above-mentioned results, we introduce a new composite iterative scheme by the viscosity approximation method. For an  -inverse-strongly monotone mapping
-inverse-strongly monotone mapping  of
of  to
to  and a nonexpansive mapping
and a nonexpansive mapping  of
of  into itself such that
into itself such that  ,
,  ,
,  ,
,  , and
, and  ,
,

If  , then the iterative scheme (1.7) reduces to the iterative scheme (1.6). Under condition (1.4) on the sequences
, then the iterative scheme (1.7) reduces to the iterative scheme (1.6). Under condition (1.4) on the sequences  and
and  and appropriate condition on sequence
and appropriate condition on sequence  , we show that the sequence
, we show that the sequence  generated by (1.7) converges strongly to a point in
generated by (1.7) converges strongly to a point in  , which is a solution of a certain variational inequality. Using this result, we also obtain a strong convergence result for finding a common fixed point of a nonexpansive mapping and a strictly pseudocontractive mapping. Moreover, we investigate the problem of finding a common point of the set of fixed points of a nonexpansive mapping and the set of zeros of an inverse-strongly monotone mapping. The main results develop and improve the corresponding results of Chen et al. [13] and Iiduka and Takahashi [10]. We point out that the iterative scheme (1.7) is a new approach for finding the fixed points of nonexpansive mappings and solutions of variational inequalities for monotone mappings.
, which is a solution of a certain variational inequality. Using this result, we also obtain a strong convergence result for finding a common fixed point of a nonexpansive mapping and a strictly pseudocontractive mapping. Moreover, we investigate the problem of finding a common point of the set of fixed points of a nonexpansive mapping and the set of zeros of an inverse-strongly monotone mapping. The main results develop and improve the corresponding results of Chen et al. [13] and Iiduka and Takahashi [10]. We point out that the iterative scheme (1.7) is a new approach for finding the fixed points of nonexpansive mappings and solutions of variational inequalities for monotone mappings.
2. Preliminaries and Lemmas
Let  be a real Hilbert space with inner product
be a real Hilbert space with inner product  and norm
and norm  , and
, and  a closed convex subset of
a closed convex subset of  . We write
. We write  to indicate that the sequence
to indicate that the sequence  converges weakly to
converges weakly to  .
.  implies that
implies that  converges strongly to
converges strongly to  . For every point
. For every point  , there exists a unique nearest point in
, there exists a unique nearest point in  , denoted by
, denoted by  , such that
, such that

for all  .
.  is called the metric projection of
is called the metric projection of  to
to  . It is well known that
. It is well known that  satisfies
satisfies

for every  . Moreover,
. Moreover,  is characterized by the properties
is characterized by the properties


for all  . In the context of the variational inequality problem, this implies that
. In the context of the variational inequality problem, this implies that

We state some examples for inverse-strongly monotone mappings. If  , where
, where  is a nonexpansive mapping of
is a nonexpansive mapping of  into itself and
into itself and  is the identity mapping of
is the identity mapping of  , then
, then  is
is  -inverse-strongly monotone and
-inverse-strongly monotone and  . A mapping
. A mapping  of
of  into
into  is called strongly monotone if there exists a positive real number
is called strongly monotone if there exists a positive real number  such that
such that

for all  . In such a case, we say that
. In such a case, we say that  is
is  -strongly monotone. If
-strongly monotone. If  is
is  -strongly monotone and
-strongly monotone and  -Lipschitz continuous, that is,
-Lipschitz continuous, that is,  for all
for all  , then
, then  is
is  -inverse-strongly monotone.
-inverse-strongly monotone.
If  is an
is an  -inverse-strongly monotone mapping of
-inverse-strongly monotone mapping of  into
into  , then it is obvious that
, then it is obvious that  is
is  -Lipschitz continuous. We also have that for all
-Lipschitz continuous. We also have that for all  and
and  ,
,

So, if  , then
, then  is a nonexpansive mapping of
is a nonexpansive mapping of  into
into  . The following result for the existence of solutions of the variational inequality problem for inverse-strongly monotone mappings was given in Takahashi and Toyoda [14].
. The following result for the existence of solutions of the variational inequality problem for inverse-strongly monotone mappings was given in Takahashi and Toyoda [14].
Proposition 2.1.
Let  be a bounded closed convex subset of a real Hilbert space and
be a bounded closed convex subset of a real Hilbert space and  an
an  -inverse-strongly monotone mapping of
-inverse-strongly monotone mapping of  into
into  . Then,
. Then,  is nonempty.
is nonempty.
A set-valued mapping  is called monotone if for all
is called monotone if for all  ,
,  and
and  imply
imply  . A monotone mapping
. A monotone mapping  is maximal if the graph
is maximal if the graph  of
of  is not properly contained in the graph of any other monotone mapping. It is known that a monotone mapping
is not properly contained in the graph of any other monotone mapping. It is known that a monotone mapping  is maximal if and only if for
is maximal if and only if for  ,
,  for every
for every  implies
implies  . Let
. Let  be an inverse-strongly monotone mapping of
be an inverse-strongly monotone mapping of  into
into  and let
and let  be the normal cone to
be the normal cone to  at
at  , that is,
, that is,  , and define
, and define

Then  is maximal monotone and
is maximal monotone and  if and only if
if and only if  ; see [15, 16].
; see [15, 16].
We need the following lemmas for the proof of our main results.
Lemma 2.2 (see [17]).
Let  be a sequence of nonnegative real numbers satisfying
be a sequence of nonnegative real numbers satisfying

where  and
and  satisfy the following conditions:
satisfy the following conditions:
(i) and
and  or, equivalently,
or, equivalently, 
(ii) or
or 
Then  .
.
Lemma 2.3 (see [1], demiclosedness principle).
Let  be a real Hilbert space,
be a real Hilbert space,  a nonempty closed convex subset of
a nonempty closed convex subset of  , and
, and  a nonexpansive mapping. Then the mapping
a nonexpansive mapping. Then the mapping  is demiclosed on
is demiclosed on  , where
, where  is the identity mapping; that is,
is the identity mapping; that is,  in
in  and
and  imply that
imply that  and
and  .
.
Lemma 2.4.
In a real Hilbert space  , there holds the following inequality:
, there holds the following inequality:

for all 
3. Main Results
In this section, we introduce a new composite iterative scheme for nonexpansive mappings and inverse-strongly monotone mappings and prove a strong convergence of this scheme.
Theorem 3.1.
Let  be a closed convex subset of a real Hilbert space
be a closed convex subset of a real Hilbert space  . Let
. Let  be an
be an  -inverse-strongly monotone mapping of
-inverse-strongly monotone mapping of  to
to  and
and  a nonexpansive mapping of
a nonexpansive mapping of  into itself such that
into itself such that  , and
, and  . Let
. Let  be a sequence generated by
be a sequence generated by

where  ,
,  , and
, and  . If
. If  ,
,  and
and  satisfy the following conditions:
satisfy the following conditions:
(i) ;
;  ;
;
(ii) for all
for all  and for some
and for some  ;
;
(iii) for some
for some  with
with  ;
;
(iv) ;
;  ;
;  ,
,
then  converges strongly to
converges strongly to  , which is a solution of the following variational inequality:
, which is a solution of the following variational inequality:

Proof.
Let  and
and  for every
for every  . Let
. Let  . Since
. Since  is nonexpansive and
is nonexpansive and  from (2.5), we have
from (2.5), we have

Similarly we have  .
.
We divide the proof into several steps.
Step 1.
We show that  is bounded. In fact, since
is bounded. In fact, since

we have

By induction, we get

This implies that  is bounded and so
is bounded and so  ,
,  ,
,  ,
,  , and
, and  are bounded. Moreover, since
are bounded. Moreover, since  and
and  ,
,  and
and  are also bounded. By condition (i), we also obtain
are also bounded. By condition (i), we also obtain

Step 2.
We show that  . From (3.1), we have
. From (3.1), we have

Simple calculations show that

Since

for every  we have
we have

for every  , where
, where  and
and  .
.
On the other hand, from (3.1) we have

Also, simple calculations show that

Since

for every  it follows that
it follows that

Substituting (3.11) into (3.15), we derive

where  and
and  . From conditions (i) and (iv), it is easy to see that
. From conditions (i) and (iv), it is easy to see that

Applying Lemma 2.2 to (3.16), we have

By (3.11), we also have that  as
as  .
.
Step 3.
We show that  and
and  . Indeed, it follows that
. Indeed, it follows that

which implies that

Obviously, by (3.7) and Step 2, we have  as
as  . This implies that
. This implies that

By (3.7) and (3.21), we also have

Step 4.
We show that  . To this end, let
. To this end, let  . Then, by convexity of
. Then, by convexity of  , we have
, we have

So we obtain

Since  and
and  by condition (i) and (3.21), we have
by condition (i) and (3.21), we have  . Moreover, from (2.2) we obtain
. Moreover, from (2.2) we obtain

and so

And hence

Then we have

Since  ,
,  and
and  , we get
, we get  . Also by (3.21), we have
. Also by (3.21), we have

Step 5.
We show that  for
for  , where
, where  is a solution of the variational inequality
is a solution of the variational inequality

To this end, choose a subsequence  of
of  such that
such that

Since  is bounded, there exists a subsequence
is bounded, there exists a subsequence  of
of  which converges weakly to
which converges weakly to  . We may assume without loss of generality that
. We may assume without loss of generality that  . Since
. Since  by Steps 4 and 5, we have
by Steps 4 and 5, we have  . Then we can obtain
. Then we can obtain  . Indeed, let us first show that
. Indeed, let us first show that  . Let
. Let

Then  is maximal monotone. Let
is maximal monotone. Let  . Since
. Since  and
and  , we have
, we have

On the other hand, from  , we have
, we have  and hence
and hence

Therefore we have

Hence we have  as
as  . Since
. Since  is maximal monotone, we have
is maximal monotone, we have  and hence
and hence  .
.
On the another hand, by Steps 3 and 4,  . So, by Lemma 2.3, we obtain
. So, by Lemma 2.3, we obtain  and hence
and hence  . Then by (3.30) we have
. Then by (3.30) we have

Thus, from (3.7) we obtain

Step 6.
We show that  for
for  , where
, where  is a solution of the variational inequality
is a solution of the variational inequality

Indeed, from Lemma 2.4, we have

where

and  . It is easily seen that
. It is easily seen that  ,
,  , and
, and  . Thus by Lemma 2.2, we obtain
. Thus by Lemma 2.2, we obtain  . This completes the proof.
. This completes the proof.
Remark 3.2.
-
(1)
Theorem 3.1 improves the corresponding results in Chen et al. [13] and Iiduka and Takahashi [10]. In particular, if
 and
and  is constant in (3.1), then Theorem 3.1 reduces to Theorem 3.1 of Iiduka and Takahashi [10].
is constant in (3.1), then Theorem 3.1 reduces to Theorem 3.1 of Iiduka and Takahashi [10]. -
(2)
We obtain a new composite iterative scheme for a nonexpansive mapping if
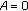 in Theorem 3.1 as follows (see also Jung [18]):
in Theorem 3.1 as follows (see also Jung [18]): 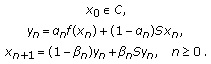 (3.41)
(3.41)
As a direct consequence of Theorem 3.1, we have the following result.
Corollary 3.3.
Let  be a closed convex subset of a real Hilbert space
be a closed convex subset of a real Hilbert space  . Let
. Let  be an
be an  -inverse-strongly monotone mapping of
-inverse-strongly monotone mapping of  to
to  such that
such that  , and
, and  . Let
. Let  be a sequence generated by
be a sequence generated by

where  ,
,  , and
, and  . If
. If  ,
,  , and
, and  satisfy the following conditions:
satisfy the following conditions:
(i) ;
;  ,
,
(ii) for all
for all  and for some
and for some  ,
,
(iii) for some
for some  with
with  ,
,
(iv) ;
;  ;
;  ,
,
then  converges strongly to
converges strongly to  , which is a solution of the following variational inequality:
, which is a solution of the following variational inequality:

4. Applications
In this section, as in [10, 13], we obtain two theorems in a Hilbert space by using Theorem 3.1.
A mapping  is called strictly pseudocontractive if there exists
is called strictly pseudocontractive if there exists  with
with  such that
such that

for every  . If
. If  , then
, then  is nonexpansive. Put
is nonexpansive. Put  , where
, where  is a strictly pseudocontractive mapping with
is a strictly pseudocontractive mapping with  . Then
. Then  is
is  -inverse-strongly monotone; see [7]. Actually, we have, for all
-inverse-strongly monotone; see [7]. Actually, we have, for all  ,
,

On the other hand, since  is a real Hilbert space, we have
is a real Hilbert space, we have

Hence we have

Using Theorem 3.1, we first get a strong convergence theorem for finding a common fixed point of a nonexpansive mapping and a strictly pseudocontractive mapping.
Theorem 4.1.
Let  be a closed convex subset of a real Hilbert space
be a closed convex subset of a real Hilbert space  . Let
. Let  be an
be an  -strictly pseudocontractive mapping of
-strictly pseudocontractive mapping of  into itself and
into itself and  a nonexpansive mapping of
a nonexpansive mapping of  into itself such that
into itself such that  , and
, and  . Let
. Let  be a sequence generated by
be a sequence generated by

where  ,
,  , and
, and  . If
. If  ,
,  , and
, and  satisfy the conditions:
satisfy the conditions:
(i) ;
;  ,
,
(ii) for all
for all  and for some
and for some  ,
,
(iii) for some
for some  with
with  ,
,
(iv) ;
;  ;
;  ,
,
then  converges strongly to
converges strongly to  , which is a solution of the following variational inequality:
, which is a solution of the following variational inequality:

Proof.
Put  . Then
. Then  is
is  -inverse-strongly monotone. We have
-inverse-strongly monotone. We have  and
and  . Thus, the desired result follows from Theorem 3.1.
. Thus, the desired result follows from Theorem 3.1.
Using Theorem 3.1, we also have the following result.
Theorem 4.2.
Let  be a real Hilbert space
be a real Hilbert space  . Let
. Let  be an
be an  -inverse-strongly monotone mapping of
-inverse-strongly monotone mapping of  into itself and
into itself and  a nonexpansive mapping of
a nonexpansive mapping of  into itself such that
into itself such that  , and
, and  . Let
. Let  be a sequence generated by
be a sequence generated by

where  ,
,  , and
, and  . If
. If  ,
,  , and
, and  satisfy the conditions:
satisfy the conditions:
(i) ;
;  ,
,
(ii) for all
for all  and for some
and for some  ,
,
(iii) for some
for some  with
with  ,
,
(iv) ;
;  ;
;  ,
,
then  converges strongly to
converges strongly to  , which is a solution of the following variational inequality:
, which is a solution of the following variational inequality:

Proof.
We have  . So, putting
. So, putting  , by Theorem 3.1, we obtain the desired result.
, by Theorem 3.1, we obtain the desired result.
Remark 4.3.
If  in Theorems 4.1 and 4.2, then Theorems 4.1 and 4.2 reduce to Chen et al. [13, Theorems 4.1 and 4.2]. Theorems 4.1 and 4.2 also extend in Iiduka and Takahashi [10, Theorems 4.1 and 4.2] to the viscosity methods in composite iterative schemes.
in Theorems 4.1 and 4.2, then Theorems 4.1 and 4.2 reduce to Chen et al. [13, Theorems 4.1 and 4.2]. Theorems 4.1 and 4.2 also extend in Iiduka and Takahashi [10, Theorems 4.1 and 4.2] to the viscosity methods in composite iterative schemes.
References
Goebel K, Kirk WA: Topics in Metric Fixed Point Theory, Cambridge Studies in Advanced Mathematics. Volume 28. Cambridge University Press, Cambridge, UK; 1990:viii+244.
Takahashi W: Nonlinear Functional Analysis: Fixed Point Theory and Its Applications. Yokohama Publishers, Yokohama, Japan; 2000:iv+276.
Browder FE: Nonlinear monotone operators and convex sets in Banach spaces. Bulletin of the American Mathematical Society 1965, 71: 780–785. 10.1090/S0002-9904-1965-11391-X
Bruck RE Jr.: On the weak convergence of an ergodic iteration for the solution of variational inequalities for monotone operators in Hilbert space. Journal of Mathematical Analysis and Applications 1977, 61(1):159–164. 10.1016/0022-247X(77)90152-4
Lions PL, Stampacchia G: Variational inequalities. Communications on Pure and Applied Mathematics 1967, 20: 493–517. 10.1002/cpa.3160200302
Takahashi W: Nonlinear complementarity problem and systems of convex inequalities. Journal of Optimization Theory and Applications 1978, 24(3):499–506. 10.1007/BF00932892
Browder FE, Petryshyn WV: Construction of fixed points of nonlinear mappings in Hilbert space. Journal of Mathematical Analysis and Applications 1967, 20: 197–228. 10.1016/0022-247X(67)90085-6
Iiduka H, Takahashi W, Toyoda M: Approximation of solutions of variational inequalities for monotone mappings. Panamerican Mathematical Journal 2004, 14(2):49–61.
Liu F, Nashed MZ: Regularization of nonlinear ill-posed variational inequalities and convergence rates. Set-Valued Analysis 1998, 6(4):313–344. 10.1023/A:1008643727926
Iiduka H, Takahashi W: Strong convergence theorems for nonexpansive mappings and inverse-strongly monotone mappings. Nonlinear Analysis: Theory, Methods & Applications 2005, 61(3):341–350. 10.1016/j.na.2003.07.023
Moudafi A: Viscosity approximation methods for fixed-points problems. Journal of Mathematical Analysis and Applications 2000, 241(1):46–55. 10.1006/jmaa.1999.6615
Xu H-K: Viscosity approximation methods for nonexpansive mappings. Journal of Mathematical Analysis and Applications 2004, 298(1):279–291. 10.1016/j.jmaa.2004.04.059
Chen J, Zhang L, Fan T: Viscosity approximation methods for nonexpansive mappings and monotone mappings. Journal of Mathematical Analysis and Applications 2007, 334(2):1450–1461. 10.1016/j.jmaa.2006.12.088
Takahashi W, Toyoda M: Weak convergence theorems for nonexpansive mappings and monotone mappings. Journal of Optimization Theory and Applications 2003, 118(2):417–428. 10.1023/A:1025407607560
Rockafellar RT: On the maximality of sums of nonlinear monotone operators. Transactions of the American Mathematical Society 1970, 149: 75–88. 10.1090/S0002-9947-1970-0282272-5
Rockafellar RT: Monotone operators and the proximal point algorithm. SIAM Journal on Control and Optimization 1976, 14(5):877–898. 10.1137/0314056
Xu H-K: An iterative approach to quadratic optimization. Journal of Optimization Theory and Applications 2003, 116(3):659–678. 10.1023/A:1023073621589
Jung JS: Strong convergence on composite iterative methods for nonexpansive mappings. Journal of the Korean Mathematical Society 2009, 46(6):1143–1156.
Acknowledgments
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (2009-0064444). The author thanks the referees for their valuable comments and suggestions, which improved the presentation of this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jung, J. A New Iteration Method for Nonexpansive Mappings and Monotone Mappings in Hilbert Spaces. J Inequal Appl 2010, 251761 (2010). https://doi.org/10.1155/2010/251761
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/251761
 and
and  is constant in (3.1), then Theorem 3.1 reduces to Theorem 3.1 of Iiduka and Takahashi [
is constant in (3.1), then Theorem 3.1 reduces to Theorem 3.1 of Iiduka and Takahashi [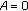 in Theorem 3.1 as follows (see also Jung [
in Theorem 3.1 as follows (see also Jung [