- Research Article
- Open access
- Published:
Poincaré Inequalities with Luxemburg Norms in  -Averaging Domains
-Averaging Domains
Journal of Inequalities and Applications volume 2010, Article number: 241759 (2010)
Abstract
We prove both local and global Poincaré inequalities with Luxemburg norms for differential forms in  -averaging domains, which can be considered as generalizations of the existing versions of Poincaré inequalities.
-averaging domains, which can be considered as generalizations of the existing versions of Poincaré inequalities.
1. Introduction
The Poincaré-type inequality has been playing a crucial role in analysis and related fields during the last several decades. Many versions of the Poincaré inequality have been developed and used in different areas of mathematics, including PDEs and analysis. For example, in 1989, Staples in [1] proved the following Poincaré inequality for Sobolev functions in  -averaging domains. If
-averaging domains. If  is an
is an  -averaging domain,
-averaging domain,  , then there exists a constant
, then there exists a constant  , such that
, such that

for each Sobolev function  defined in
defined in  . In [2], a global Poincaré inequality for solutions of the
. In [2], a global Poincaré inequality for solutions of the  -harmonic equation was proved over the John domains; see [3–7] for more results about the Poincaré inequality. However, most of these inequalities are developed with the
-harmonic equation was proved over the John domains; see [3–7] for more results about the Poincaré inequality. However, most of these inequalities are developed with the  -norms. In this paper, we will establish the Poincaré inequalities with the Luxemburg norms in a relative large class of domains, the
-norms. In this paper, we will establish the Poincaré inequalities with the Luxemburg norms in a relative large class of domains, the  -averaging domain, so that many existing versions of the Poincaré inequality are special cases of our new results.
-averaging domain, so that many existing versions of the Poincaré inequality are special cases of our new results.
Let  be a bounded domain in
be a bounded domain in  ,
,  , and let
, and let  and
and  be the balls with the same center and
be the balls with the same center and  throughout this paper. The
throughout this paper. The  -dimensional Lebesgue measure of a set
-dimensional Lebesgue measure of a set 
 is denoted by
is denoted by  . For a function
. For a function  , we denote the average of
, we denote the average of  over
over  by
by  . All integrals involved in this paper are the Lebesgue integrals. Differential forms are generalizations of differentiable functions in
. All integrals involved in this paper are the Lebesgue integrals. Differential forms are generalizations of differentiable functions in  . For example, the function
. For example, the function  is called a
is called a  -form. A differential
-form. A differential  -form
-form  in
in  can be written as
can be written as  , where the coefficient functions
, where the coefficient functions  ,
,  , are differentiable. Similarly, a differential
, are differentiable. Similarly, a differential  -form
-form  can be expressed as
can be expressed as

where  ,
,  . Let
. Let  be the set of all
be the set of all  -forms in
-forms in  ,
,  be the space of all differential
be the space of all differential  -forms in
-forms in  , and let
, and let  be the
be the  -forms
-forms  in
in  satisfying
satisfying  for all ordered
for all ordered  -tuples
-tuples  ,
,  . We denote the exterior derivative by
. We denote the exterior derivative by  and the Hodge star operator by
and the Hodge star operator by  . The Hodge codifferential operator
. The Hodge codifferential operator  is given by
is given by  ,
,  . We consider here the nonlinear partial differential equation
. We consider here the nonlinear partial differential equation

which is called nonhomogeneous  -harmonic equation, where
-harmonic equation, where  and
and  satisfy the conditions
satisfy the conditions  ,
,  and
and  for almost every
for almost every  and all
and all  . Here
. Here  are constants and
are constants and  is a fixed exponent associated with (1.3). A solution to (1.3) is an element of the Sobolev space
is a fixed exponent associated with (1.3). A solution to (1.3) is an element of the Sobolev space  such that
such that  for all
for all  with compact support. If
with compact support. If  is a function (
is a function ( -form) in
-form) in  , (1.3) reduces to
, (1.3) reduces to

If the operator  , (1.3) becomes
, (1.3) becomes

which is called the (homogeneous)  -harmonic equation. Let
-harmonic equation. Let  be defined by
be defined by  with
with  . Then,
. Then,  satisfies the required conditions and (1.5) becomes the
satisfies the required conditions and (1.5) becomes the  -harmonic equation
-harmonic equation  for differential forms. See [8–12] for recent results on the
for differential forms. See [8–12] for recent results on the  -harmonic equations and related topics.
-harmonic equations and related topics.
2. Local Poincaré Inequalities
In this section, we establish the local Poincaré inequalities for the differential forms in any bounded domain. A continuously increasing function  with
with  is called an Orlicz function. The Orlicz space
is called an Orlicz function. The Orlicz space  consists of all measurable functions
consists of all measurable functions  on
on  such that
such that  for some
for some  .
.  is equipped with the nonlinear Luxemburg functional
is equipped with the nonlinear Luxemburg functional

A convex Orlicz function  is often called a Young function. If
is often called a Young function. If  is a Young function, then
is a Young function, then  defines a norm in
defines a norm in  , which is called the Luxemburg norm.
, which is called the Luxemburg norm.
Definition 2.1 (see [13]).
We say that a Young function  lies in the class
lies in the class  ,
,  ,
,  , if (i)
, if (i)  and (ii)
and (ii)  for all
for all  , where
, where  is a convex increasing function and
is a convex increasing function and  is a concave increasing function on
is a concave increasing function on  .
.
From [13], each of  and
and  in above definition is doubling in the sense that its values at
in above definition is doubling in the sense that its values at  and
and  are uniformly comparable for all
are uniformly comparable for all  , and the consequent fact that
, and the consequent fact that

where  and
and  are constants. Also, for all
are constants. Also, for all  and
and  , the function
, the function  belongs to
belongs to  for some constant
for some constant  . Here
. Here  is defined by
is defined by  for
for  ; and
; and  for
for  . Particularly, if
. Particularly, if  , we see that
, we see that  lies in
lies in  ,
,  . We will need the following Reverse Hölder inequality.
. We will need the following Reverse Hölder inequality.
Lemma 2.2 (see [8]).
Let  be a solution of the nonhomogeneous
be a solution of the nonhomogeneous  -harmonic equation (1.3) in a domain
-harmonic equation (1.3) in a domain  an d let
an d let  . Then, there exists a constant
. Then, there exists a constant  , independent of
, independent of  , such that
, such that  for all balls
for all balls  with
with  for some
for some  .
.
We first prove the following generalized Poincaré inequality that will be used to establish the global inequality.
Theorem.
Let  be a Young function in the class
be a Young function in the class  ,
,  ,
,  , and
, and  be a bounded domain. Assume that
be a bounded domain. Assume that  and
and  is a solution of the nonhomogeneous
is a solution of the nonhomogeneous  -harmonic equation (1.3) in
-harmonic equation (1.3) in  ,
,  . Then for any ball
. Then for any ball  with
with  , there exists a constant
, there exists a constant  , independent of
, independent of  , such that
, such that

Proof.
From [7, ( )], we have
)], we have

for any  . Note that if
. Note that if  is a solution of the nonhomogeneous
is a solution of the nonhomogeneous  -harmonic equation (1.3), then
-harmonic equation (1.3), then  is also a solution of (1.3) since
is also a solution of (1.3) since  is a closed form. From Lemma 2.2, it follows that
is a closed form. From Lemma 2.2, it follows that

for any positive numbers  and
and  . From (2.5), (i) in Definition 2.1, and using the fact that
. From (2.5), (i) in Definition 2.1, and using the fact that  is an increasing function, Jensen's inequality, and noticing that
is an increasing function, Jensen's inequality, and noticing that  and
and  are doubling, we have
are doubling, we have

Since  , then
, then  . Hence, we have
. Hence, we have  From (i) in Definition 2.1, we find that
From (i) in Definition 2.1, we find that  . Thus,
. Thus,

Combining (2.6) and (2.7) yields

Using Jensen's inequality for  , (2.2), and noticing that
, (2.2), and noticing that  and
and  are doubling, we obtain
are doubling, we obtain

Substituting (2.8) into (2.9) and noticing that  is doubling, we have
is doubling, we have

We have completed the proof of Theorem 2.3.
Since each of  , and
, and  in Definition 2.1 is doubling, from the proof of Theorem 2.3 or directly from (2.3), we have
in Definition 2.1 is doubling, from the proof of Theorem 2.3 or directly from (2.3), we have

for all balls  with
with  and any constant
and any constant  . From (2.1) and (2.11), the following Poincaré inequality with the Luxemburg norm
. From (2.1) and (2.11), the following Poincaré inequality with the Luxemburg norm

holds under the conditions described in Theorem 2.3.
Theorem.
Let  be a Young function in the class
be a Young function in the class  ,
,  ,
,  , let
, let  be a bounded domain and
be a bounded domain and  . Assume that
. Assume that  is any differential
is any differential  -form,
-form,  ,
,  and
and  . Then for any ball
. Then for any ball  , there exists a constant
, there exists a constant  , independent of
, independent of  , such that
, such that

Proof.
From (2.9), it follows that

If  , by assumption, we have
, by assumption, we have  . Using the Poincaré-type inequality for differential forms
. Using the Poincaré-type inequality for differential forms

we find that

Note that the  -norm of
-norm of  increases with
increases with  and
and  as
as  , and it follows that (2.16) still holds when
, and it follows that (2.16) still holds when  . Since
. Since  is increasing, from (2.14) and (2.16), we obtain
is increasing, from (2.14) and (2.16), we obtain

Applying (2.17), (i) in Definition 2.1, Jensen's inequality, and noticing that  and
and  are doubling, we have
are doubling, we have

Using (i) in Definition 2.1 again yields

Combining (2.18) and (2.19), we obtain

The proof of Theorem 2.4 has been completed.
Similar to (2.12), from (2.1) and (2.13), the following Luxemburg norm Poincaré inequality

holds if all conditions of Theorem 2.4 are satisfied.
3. Global Poincaré Inequalities
In this section, we extend the local Poincaré inequalities into the global cases in the following  -averaging domains.
-averaging domains.
Definition 3.1 (see [14]).
Let  be an increasing convex function on
be an increasing convex function on  with
with  . We call a proper subdomain
. We call a proper subdomain  an
an  -averaging domain, if
-averaging domain, if  and there exists a constant C such that
and there exists a constant C such that

for some ball  and all
and all  such that
such that  , where
, where  are constants with
are constants with  ,
,  and the supremum is over all balls
and the supremum is over all balls  .
.
From above definition we see that  -averaging domains and
-averaging domains and  -averaging domains are special
-averaging domains are special  -averaging domains when
-averaging domains when  in Definition 3.1. Also, uniform domains and John domains are very special
in Definition 3.1. Also, uniform domains and John domains are very special  -averaging domains; see [15–18] for more results about domains.
-averaging domains; see [15–18] for more results about domains.
Theorem.
Let  be a Young function in the class
be a Young function in the class  ,
,  ,
,  , an d let
, an d let  be any bounded
be any bounded  -averaging domain. Assume that
-averaging domain. Assume that  and
and  is a solution of the nonhomogeneous
is a solution of the nonhomogeneous  -harmonic equation (1.4) in
-harmonic equation (1.4) in  ,
,  . Then, there exists a constant
. Then, there exists a constant  , independent of
, independent of  , such that
, such that

where  is some fixed ball.
is some fixed ball.
Proof.
From Definition 3.1, (2.3) and noticing that  is doubling, we have
is doubling, we have

We have completed the proof of Theorem 3.2.
Similar to the local case, the following global Poincaré inequality with the Luxemburg norm

holds if all conditions in Theorem 3.2 are satisfied. Also, by the same way, we can extend Theorem 2.4 into the following global result in  -averaging domains.
-averaging domains.
Theorem.
Let  be a Young function in the class
be a Young function in the class  ,
,  ,
,  ,
,  be a bounded
be a bounded  -averaging domain and
-averaging domain and  . Assume that
. Assume that  and
and  and
and  . Then, there exists a constant
. Then, there exists a constant  , independent of
, independent of  , such that
, such that

where  is some fixed ball.
is some fixed ball.
Note that (3.5) can be written as

It has been proved that any John domain is a special  -averaging domain. Hence, we have the following results.
-averaging domain. Hence, we have the following results.
Corollary.
Let  be a Young function in the class
be a Young function in the class  ,
,  ,
,  , and
, and  be a bounded John domain. Assume that
be a bounded John domain. Assume that  and
and  is a solution of the nonhomogeneous
is a solution of the nonhomogeneous  -harmonic equation (1.4) in
-harmonic equation (1.4) in  ,
,  . Then, there exists a constant
. Then, there exists a constant  , independent of
, independent of  , such that
, such that

where  is some fixed ball.
is some fixed ball.
Choosing  in Theorems 3.2 and 3.3, respectively, we obtain the following Poincaré inequalities with the
in Theorems 3.2 and 3.3, respectively, we obtain the following Poincaré inequalities with the  -norms.
-norms.
Corollary.
Let  ,
,  and
and  . Assume that
. Assume that  and
and  is a solution of the nonhomogeneous
is a solution of the nonhomogeneous  -harmonic equation (1.4),
-harmonic equation (1.4),  . Then, there exists a constant
. Then, there exists a constant  , independent of
, independent of  , such that
, such that

for any bounded  -averaging domain
-averaging domain  and
and  is some fixed ball.
is some fixed ball.
Note that (3.8) can be written as the following version with the Luxemburg norm:

provided that the conditions in Corollary 3.5 are satisfied.
Corollary.
Let  ,
,  and
and  and
and  be a bounded
be a bounded  -averaging domain and
-averaging domain and  . Assume that
. Assume that  ,
,  , and
, and  Then, there exists a constant
Then, there exists a constant  , independent of
, independent of  , such that
, such that

where  is some fixed ball.
is some fixed ball.
4. Applications
Choose  to be a
to be a  -form (a function) in the homogeneous
-form (a function) in the homogeneous  -harmonic equation (1.5). Then, (1.5) reduces to the following
-harmonic equation (1.5). Then, (1.5) reduces to the following  -harmonic equation:
-harmonic equation:

for functions. If the above operator  is defined by
is defined by  with
with  , then,
, then,  satisfies the required conditions and (4.1) becomes the usual
satisfies the required conditions and (4.1) becomes the usual  -harmonic equation
-harmonic equation

for functions. Thus, from Theorem 3.2, we have the following example.
Example.
Let  be a solution of the usual
be a solution of the usual  -harmonic equation (4.1) or the
-harmonic equation (4.1) or the  -harmonic equation (4.2), let
-harmonic equation (4.2), let  be a Young function in the class
be a Young function in the class  ,
,  ,
,  , and
, and  be any bounded
be any bounded  -averaging domain. If
-averaging domain. If  and
and  , then there exists a constant
, then there exists a constant  , independent of
, independent of  , such that
, such that

where  is some fixed ball.
is some fixed ball.
Example.
For any locally  -integrable form
-integrable form  ,
,  , the Hardy-Littlewood maximal operator
, the Hardy-Littlewood maximal operator  is defined by
is defined by  and the sharp maximal operator
and the sharp maximal operator  by
by  where
where  is the ball of radius
is the ball of radius  , centered at
, centered at  . Under the conditions of Theorem 3.3, we have
. Under the conditions of Theorem 3.3, we have

where  is some fixed ball.
is some fixed ball.
Remark.
-
(i)
We know that the
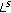 -averaging domains are the special
-averaging domains are the special 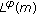 -averaging domains. Thus, Theorems 3.2 and 3.3 also hold for the
-averaging domains. Thus, Theorems 3.2 and 3.3 also hold for the 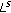 -averaging domain. (ii) In Theorems 2.4 and 3.3,
-averaging domain. (ii) In Theorems 2.4 and 3.3,  does not need to be a solution of any version of the
does not need to be a solution of any version of the 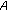 -harmonic equation.
-harmonic equation.
References
Staples SG:
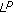 -averaging domains and the Poincaré inequality. Annales Academiae Scientiarum Fennicae. Series A I. Mathematica 1989, 14(1):103–127.
-averaging domains and the Poincaré inequality. Annales Academiae Scientiarum Fennicae. Series A I. Mathematica 1989, 14(1):103–127.Ding S, Nolder CA: Weighted Poincaré inequalities for solutions to -harmonic equations. Illinois Journal of Mathematics 2002, 46(1):199–205.
Wang Y: Two-weight Poincaré-type inequalities for differential forms in -averaging domains. Applied Mathematics Letters 2007, 20(11):1161–1166. 10.1016/j.aml.2007.02.003
Wang Y, Wu C: Global Poincaré inequalities for Green's operator applied to the solutions of the nonhomogeneous -harmonic equation. Computers and Mathematics with Applications 2004, 47(10–11):1545–1554. 10.1016/j.camwa.2004.06.006
Xing Y: Weighted Poincaré-type estimates for conjugate -harmonic tensors. Journal of Inequalities and Applications 2005, (1):1–6.
Liu B:
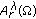 -weighted imbedding inequalities for -harmonic tensors. Journal of Mathematical Analysis and Applications 2002, 273(2):667–676. 10.1016/S0022-247X(02)00331-1
-weighted imbedding inequalities for -harmonic tensors. Journal of Mathematical Analysis and Applications 2002, 273(2):667–676. 10.1016/S0022-247X(02)00331-1Xing Y, Ding S: Poincaré inequalities with the Radon measure for differential forms. Computers and Mathematics with Applications, Accepted Computers and Mathematics with Applications, Accepted
Nolder CA: Hardy-Littlewood theorems for -harmonic tensors. Illinois Journal of Mathematics 1999, 43(4):613–632.
Ding S: Two-weight Caccioppoli inequalities for solutions of nonhomogeneous -harmonic equations on Riemannian manifolds. Proceedings of the American Mathematical Society 2004, 132(8):2367–2375. 10.1090/S0002-9939-04-07347-2
Agarwal RP, O'Regan D, Shakhmurov VB: Separable anisotropic differential operators in weighted abstract spaces and applications. Journal of Mathematical Analysis and Applications 2008, 338(2):970–983. 10.1016/j.jmaa.2007.05.078
Agarwal RP, Diagana T, Hernández EM: Weighted pseudo almost periodic solutions to some partial neutral functional differential equations. Journal of Nonlinear and Convex Analysis 2007, 8(3):397–415.
Yuming X: Weighted integral inequalities for solutions of the -harmonic equation. Journal of Mathematical Analysis and Applications 2003, 279(1):350–363. 10.1016/S0022-247X(03)00036-2
Buckley SM, Koskela P: Orlicz-Hardy inequalities. Illinois Journal of Mathematics 2004, 48(3):787–802.
Ding S:
 -averaging domains and the quasi-hyperbolic metric. Computers & Mathematics with Applications 2004, 47(10–11):1611–1618. 10.1016/j.camwa.2004.06.016
-averaging domains and the quasi-hyperbolic metric. Computers & Mathematics with Applications 2004, 47(10–11):1611–1618. 10.1016/j.camwa.2004.06.016Ding S, Nolder CA:
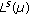 -averaging domains. Journal of Mathematical Analysis and Applications 2003, 283(1):85–99. 10.1016/S0022-247X(03)00216-6
-averaging domains. Journal of Mathematical Analysis and Applications 2003, 283(1):85–99. 10.1016/S0022-247X(03)00216-6Agarwal RP, Ding S, Nolder CA: Inequalities for Differential Forms. Springer, New York, NY, USA; 2009:xvi+387.
Staples SG: Averaging domains: from Euclidean spaces to homogeneous spaces. In Differential & Difference Equations and Applications. Hindawi, New York, NY, USA; 2006:1041–1048.
Stein EM: Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals, Princeton Mathematical Series. Volume 43. Princeton University Press, Princeton, NJ, USA; 1993:xiv+695.
Acknowledgments
The author was supported by the NSF of China (no. 10771044) and by the Science Research Foundation at Harbin Institute of Technology (HITC200709).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xing, Y. Poincaré Inequalities with Luxemburg Norms in  -Averaging Domains.
J Inequal Appl 2010, 241759 (2010). https://doi.org/10.1155/2010/241759
-Averaging Domains.
J Inequal Appl 2010, 241759 (2010). https://doi.org/10.1155/2010/241759
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/241759
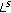 -averaging domains are the special
-averaging domains are the special 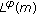 -averaging domains. Thus, Theorems 3.2 and 3.3 also hold for the
-averaging domains. Thus, Theorems 3.2 and 3.3 also hold for the 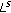 -averaging domain. (ii) In Theorems 2.4 and 3.3,
-averaging domain. (ii) In Theorems 2.4 and 3.3,  does not need to be a solution of any version of the
does not need to be a solution of any version of the 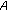 -harmonic equation.
-harmonic equation.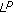 -averaging domains and the Poincaré inequality. Annales Academiae Scientiarum Fennicae. Series A I. Mathematica 1989, 14(1):103–127.
-averaging domains and the Poincaré inequality. Annales Academiae Scientiarum Fennicae. Series A I. Mathematica 1989, 14(1):103–127.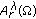 -weighted imbedding inequalities for -harmonic tensors. Journal of Mathematical Analysis and Applications 2002, 273(2):667–676. 10.1016/S0022-247X(02)00331-1
-weighted imbedding inequalities for -harmonic tensors. Journal of Mathematical Analysis and Applications 2002, 273(2):667–676. 10.1016/S0022-247X(02)00331-1 -averaging domains and the quasi-hyperbolic metric. Computers & Mathematics with Applications 2004, 47(10–11):1611–1618. 10.1016/j.camwa.2004.06.016
-averaging domains and the quasi-hyperbolic metric. Computers & Mathematics with Applications 2004, 47(10–11):1611–1618. 10.1016/j.camwa.2004.06.016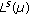 -averaging domains. Journal of Mathematical Analysis and Applications 2003, 283(1):85–99. 10.1016/S0022-247X(03)00216-6
-averaging domains. Journal of Mathematical Analysis and Applications 2003, 283(1):85–99. 10.1016/S0022-247X(03)00216-6