- Research Article
- Open access
- Published:
Generalized Bi-Quasivariational Inequalities for Quasi-Pseudomonotone Type II Operators on Noncompact Sets
Journal of Inequalities and Applications volume 2010, Article number: 237191 (2010)
Abstract
We prove some existence results of solutions for a new class of generalized bi-quasivariational inequalities (GBQVI) for quasi-pseudomonotone type II and strongly quasi-pseudomonotone type II operators defined on noncompact sets in locally convex Hausdorff topological vector spaces. To obtain these results on GBQVI for quasi-pseudomonotone type II and strongly quasi-pseudomonotone type II operators, we use Chowdhury and Tan's generalized version (1996) of Ky Fan's minimax inequality (1972) as the main tool.
1. Introduction and Preliminaries
In this paper, we obtain some results on generalized bi-quasi-variational inequalities for quasi-pseudo-monotone type II and strongly quasi-pseudo-monotone type II operators defined on noncompact sets in locally convex Hausdorff topological vector spaces. Thus we begin this section by defining the generalized bi-quasi-variational inequalities. For this, we need to introduce some notations which will be used throughout this paper.
Let  be a nonempty set and let
be a nonempty set and let  be the family of all nonempty subsets of
be the family of all nonempty subsets of  . If
. If  and
and  are topological spaces and
are topological spaces and  , then the graph of
, then the graph of  is the set
is the set  . Throughout this paper,
. Throughout this paper,  denotes either the real field
denotes either the real field  or the complex field
or the complex field  .
.
Let  be a topological vector space over
be a topological vector space over  , let
, let  be a vector space over
be a vector space over  and let
and let  be a bilinear functional.
be a bilinear functional.
For any  , any nonempty subset
, any nonempty subset  of
of  , and any
, and any  , let
, let  and
and  . Let
. Let  be the (weak) topology on
be the (weak) topology on  generated by the family
generated by the family  as a subbase for the neighbourhood system at 0 and let
as a subbase for the neighbourhood system at 0 and let  be the (strong) topology on
be the (strong) topology on  generated by the family
generated by the family  is a nonempty bounded subset of
is a nonempty bounded subset of  and
and  as a base for the neighbourhood system at 0. We note then that
as a base for the neighbourhood system at 0. We note then that  , when equipped with the (weak) topology
, when equipped with the (weak) topology  or the (strong) topology
or the (strong) topology  , becomes a locally convex topological vector space which is not necessarily Hausdorff. But, if the bilinear functional
, becomes a locally convex topological vector space which is not necessarily Hausdorff. But, if the bilinear functional  separates points in
separates points in  , that is, for any
, that is, for any  with
with  , there exists
, there exists  such that
such that  , then
, then  also becomes Hausdorff. Furthermore, for any net
also becomes Hausdorff. Furthermore, for any net  in
in  and
and  ,
,
(1) in
in  if and only if
if and only if  for any
for any  ,
,
(2) in
in  if and only if
if and only if  uniformly for any
uniformly for any  , where a nonempty bounded subset of
, where a nonempty bounded subset of  .
.
The generalized bi-quasi-variational inequality problem was first introduced by Shih and Tan [1] in 1989. Since Shih and Tan, some authors have obtained many results on generalized (quasi)variational inequalities, generalized (quasi)variational-like inequalities and generalized bi-quasi-variational inequalities (see [2–15]).
The following is the definition due to Shih and Tan [1].
Definition 1.1 ..
Let  and
and  be a vector spaces over
be a vector spaces over  , let
, let  be a bilinear functional, and let
be a bilinear functional, and let  be a nonempty subset of
be a nonempty subset of  . If
. If  and
and  , the generalized bi-quasi variational inequality problem (GBQVI) for the triple (
, the generalized bi-quasi variational inequality problem (GBQVI) for the triple ( ,
,  ,
,  ) is to find
) is to find  satisfying the following properties:
satisfying the following properties:
(1) ,
,
(2) for any
for any  and
and  .
.
The following definition of the generalized bi-quasi-variational inequality problem is a slight modification of Definition 1.1.
Definition 1.2.
Let  and
and  be vector spaces over
be vector spaces over  , let
, let  be a bilinear functional, and let
be a bilinear functional, and let  be a nonempty subset of
be a nonempty subset of  . If
. If  and
and  , then the generalized bi-quasivariational inequality (GBQVI) problem for the triple (
, then the generalized bi-quasivariational inequality (GBQVI) problem for the triple ( ,
,  ,
,  ) is:
) is:
(1)to find a point  and a point
and a point  such that
such that

(2)to find a point  , a point
, a point  , and a point
, and a point  such that
such that

Let  be a nonempty subset of
be a nonempty subset of  and let
and let  be a set-valued mapping. Then
be a set-valued mapping. Then  is said to be monotone on
is said to be monotone on  if, for any
if, for any  ,
,  , and
, and 
 .
.
Let  and
and  be topological spaces and let
be topological spaces and let  be a set-valued mapping. Then
be a set-valued mapping. Then  is said to be:
is said to be:
(1)upper (resp., lower) semicontinuous at  if, for each open set
if, for each open set  in
in  with
with  (resp.,
(resp.,  ), there exists an open neighbourhood
), there exists an open neighbourhood  of
of  in
in  such that
such that  (resp.,
(resp.,  ) for all
) for all  ,
,
(2)upper (resp., lower) semicontinuous on  if
if  is upper (resp., lower) semicontinuous at each point of
is upper (resp., lower) semicontinuous at each point of  ,
,
(3)continuous on  if
if  is both lower and upper semi-continuous on
is both lower and upper semi-continuous on  .
.
Let  be a convex set in a topological vector space
be a convex set in a topological vector space  . Then
. Then  is said to be lower semi-continuous if, for all
is said to be lower semi-continuous if, for all  ,
,  is closed in
is closed in  .
.
If  is a convex set in a vector space
is a convex set in a vector space  , then
, then  is said to be concave if, for all
is said to be concave if, for all  and
and  ,
,

Our main results in this paper are to obtain some existence results of solutions of the generalized bi-quasi-variational inequalities using Chowdhury and Tan's following definition of quasi-pseudo-monotone type II and strongly quasi-pseudo-monotone type II operators given in [3].
Definition 1.3.
Let  be a topological vector space, let
be a topological vector space, let  be a nonempty subset of
be a nonempty subset of  , and let
, and let  be a topological vector space over
be a topological vector space over  . Let
. Let  be a bilinear functional. Consider a mapping
be a bilinear functional. Consider a mapping  and two set-valued mappings
and two set-valued mappings  and
and  .
.
(1) is called an
is called an  -quasi-pseudo-monotone (resp., strongly
-quasi-pseudo-monotone (resp., strongly -quasi-pseudo-monotone) type II operator if, for any
-quasi-pseudo-monotone) type II operator if, for any  and every net
and every net  in
in  converging to
converging to  (resp., weakly to
(resp., weakly to  ) with
) with

(2) is said to be a quasi-pseudo-monotone (resp., strongly quasi-pseudo-monotone) type II operator if
is said to be a quasi-pseudo-monotone (resp., strongly quasi-pseudo-monotone) type II operator if  is an
is an  -quasi-pseudo-monotone (resp., strongly
-quasi-pseudo-monotone (resp., strongly  -quasi-pseudo-monotone) type II operator with
-quasi-pseudo-monotone) type II operator with  .
.
The following is an example on quasi-pseudo-monotone type II operators given in [3].
Example 1.4.
Consider  and
and  . Then
. Then  . Let
. Let  be a set-valued mapping defined by
be a set-valued mapping defined by

Again, let  be a set-valued mapping defined by
be a set-valued mapping defined by

Then  is lower semi-continuous and
is lower semi-continuous and  is upper semi-continuous. It can be shown that
is upper semi-continuous. It can be shown that  becomes a quasi-pseudo-monotone type II operator on
becomes a quasi-pseudo-monotone type II operator on  .
.
-
(i)
To show that
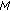 is lower semi-continuous, consider
is lower semi-continuous, consider 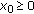 . Then
. Then 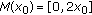 . Let
. Let 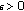 be given. Then, if
be given. Then, if 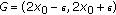 , then
, then 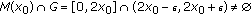 . Let
. Let 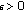 be so chosen that
be so chosen that 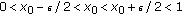 . Now, if we take
. Now, if we take 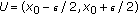 , then, for all
, then, for all 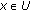 , we have
, we have  . Thus
. Thus  . Hence
. Hence 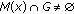 .
.
If  ,
,  . Then, for
. Then, for  , we can take
, we can take  . Thus for all
. Thus for all  ,
,  because
because  implies
implies  .
.
Finally, if  , then
, then  . We take
. We take  for some
for some  so that
so that  and
and  . Thus, for all
. Thus, for all  , we have
, we have  . Hence
. Hence  , where
, where  for
for  . Consequently,
. Consequently,  is lower semi-continuous on
is lower semi-continuous on  .
.
-
(ii)
To show that
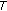 is upper semi-continuous, let
is upper semi-continuous, let 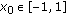 be such that
be such that  . Then
. Then 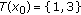 . Let
. Let 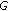 be an open set in
be an open set in 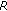 such that
such that  . Let
. Let  be such that
be such that 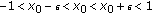 . Consider
. Consider 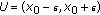 . Then, for all
. Then, for all 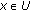 ,
, 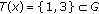 since
since 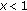 . Again, if
. Again, if 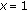 , then
, then 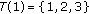 . Let
. Let 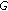 be an open set in
be an open set in 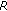 such that
such that 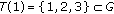 . Let
. Let 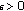 be such that
be such that 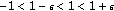 . Let
. Let 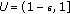 which is an open neighbourhood of
which is an open neighbourhood of 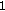 in
in 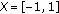 . Then for all
. Then for all 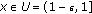 , we have
, we have 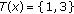 if
if 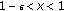 and
and 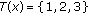 if
if 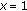 . Now,
. Now, 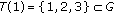 . Also, for all
. Also, for all 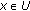 with
with 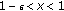 , we have
, we have 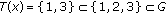 . Hence
. Hence 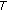 is upper semi-continuous on
is upper semi-continuous on 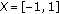 .
. -
(iii)
Finally, we will show that
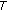 is also a quasi-pseudo-monotone type II operator. To show this, let us assume first that
is also a quasi-pseudo-monotone type II operator. To show this, let us assume first that 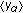 is a net in
is a net in 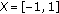 such that
such that 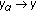 in
in 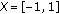 . We now show that
. We now show that 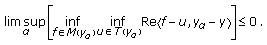 (1.7)
(1.7)
We have

(considering  , the value will be also
, the value will be also  if we consider
if we consider  ). So, it follows that, for all
). So, it follows that, for all  ,
,

The values can be obtained similarly for the cases where  and
and  . Also, it follows that, for all
. Also, it follows that, for all  ,
,

The values can be obtained similarly for the cases when  . Therefore, in all the cases, we have shown that
. Therefore, in all the cases, we have shown that

Hence  is a quasi-pseudo-monotone type II operator.
is a quasi-pseudo-monotone type II operator.
The above example is a particular case of a more general result on quasi-pseudo-monotone type II operators. We will establish this result in the following proposition.
Proposition 1.5.
Let  be a nonempty compact subset of a topological vector space
be a nonempty compact subset of a topological vector space  . Suppose that
. Suppose that  and
and  are two set-valued mappings such that
are two set-valued mappings such that  is lower semi-continuous and
is lower semi-continuous and  is upper semi-continuous. Suppose further that, for any
is upper semi-continuous. Suppose further that, for any  ,
,  and
and  are weak*-compact sets in
are weak*-compact sets in  . Then
. Then  is both a quasi-pseudo-monotone type II and a strongly quasi-pseudo-monotone type II operator.
is both a quasi-pseudo-monotone type II and a strongly quasi-pseudo-monotone type II operator.
Proof.
Suppose that  is a net in
is a net in  and
and  with
with  (resp.,
(resp.,  weakly) and
weakly) and  . Then it follows that, for any
. Then it follows that, for any  ,
,

To obtain the above inequalities, we use the following facts. For any  ,
,  and
and  . Since
. Since  is compact and
is compact and  and
and  are weak*-compact valued for any
are weak*-compact valued for any  , using the lower semicontinuity of
, using the lower semicontinuity of  and the upper semicontinuity of
and the upper semicontinuity of  it can be shown that (details can be verified by the reader easily)
it can be shown that (details can be verified by the reader easily)  and
and  . Thus we obtain
. Thus we obtain

in the last inequality above. Consequently,  is both a quasi-pseudo-monotone type II and a strongly quasi-pseudo-monotone type II operator.
is both a quasi-pseudo-monotone type II and a strongly quasi-pseudo-monotone type II operator.
In Section 3 of this paper, we obtain some general theorems on solutions for a new class of generalized bi-quasi-variational inequalities for quasi-pseudo-monotone type II and strongly quasi-pseudo-monotone type II operators defined on noncompact sets in topological vector spaces. To obtain these results, we mainly use the following generalized version of Ky Fan's minimax inequality [16] due to Chowdhury and Tan [17].
Theorem 1.6.
Let  be a topological vector space, let
be a topological vector space, let  be a nonempty convex subset of
be a nonempty convex subset of  , and let
, and let  be such that
be such that
(a)for any  and fixed
and fixed  ,
,  is lower semi-continuous on
is lower semi-continuous on  ,
,
(b)for any  and
and  ,
,  ,
,
(c)for any  and
and  , every net
, every net  in
in  converging to
converging to  with
with  for all
for all  and
and  , one has
, one has  ,
,
(d)there exist a nonempty closed and compact subset  of
of  and
and  such that
such that  for all
for all  .
.
Then there exists  such that
such that  for all
for all  .
.
Now, we use the following lemmas for our main results in this paper.
Lemma 1.7 (see [18]).
Let  be a nonempty subset of a Hausdorff topological vector space
be a nonempty subset of a Hausdorff topological vector space  and let
and let  be an upper semi-continuous mapping such that
be an upper semi-continuous mapping such that  is a bounded subset of
is a bounded subset of  for any
for any  . Then, for any continuous linear functional
. Then, for any continuous linear functional  on
on  , the mapping
, the mapping  defined by
defined by  is upper semi-continuous; that is, for any
is upper semi-continuous; that is, for any  , the set
, the set  is open in
is open in  .
.
Let  and
and  be topological spaces, let
be topological spaces, let  be nonnegative and continuous and let
be nonnegative and continuous and let  be lower semi-continuous. Then the mapping
be lower semi-continuous. Then the mapping  defined by
defined by  for all
for all  is lower semi-continuous.
is lower semi-continuous.
Let  be a nonempty convex subset of a vector space and let
be a nonempty convex subset of a vector space and let  be a nonempty compact convex subset of a Hausdorff topological vector space. Suppose that
be a nonempty compact convex subset of a Hausdorff topological vector space. Suppose that  is a real-valued function on
is a real-valued function on  such that, for each fixed
such that, for each fixed  , the mapping
, the mapping  , that is,
, that is,  is lower semi-continuous and convex on
is lower semi-continuous and convex on  and, for each fixed
and, for each fixed  , the mapping
, the mapping  , that is,
, that is,  is concave on
is concave on  . Then
. Then

2. Existence Results
In this section, we will obtain and prove some existence theorems for the solutions to the generalized bi-quasi-variational inequalities of quasi-pseudo-monotone type II and strongly quasi-pseudo-monotone type II operators with noncompact domain in locally convex Hausdorff topological vector spaces. Our results extend and/or generalize the corresponding results in [1].
Before we establish our main results, we state the following result which is Lemma 3.1 in [3].
Lemma 2.1.
Let  be a Hausdorff topological vector space over
be a Hausdorff topological vector space over  , let
, let  be a vector space over
be a vector space over  , and let
, and let  be a nonempty compact subset of
be a nonempty compact subset of  . Let
. Let  be a bilinear functional such that
be a bilinear functional such that  separates points in
separates points in  . Suppose that the
. Suppose that the  equips with the
equips with the  -topology; for any
-topology; for any  ,
,  is continuous on
is continuous on  and
and  ,
,  are upper semi-continuous maps such that
are upper semi-continuous maps such that  and
and  are compact for any
are compact for any  . Let
. Let  and
and  be continuous. Define a mapping
be continuous. Define a mapping  by
by

Suppose that  is continuous over the
is continuous over the  compact
compact subset
subset  of
of  . Then
. Then  is lower semi-continuous on
is lower semi-continuous on  .
.
Now, we establish our first main result as follows.
Theorem 2.2.
Let  be a locally convex Hausdorff topological vector space over
be a locally convex Hausdorff topological vector space over  , let
, let  be a nonempty paracompact convex and bounded subset of
be a nonempty paracompact convex and bounded subset of  , and let
, and let  be a Hausdorff topological vector space over
be a Hausdorff topological vector space over  . Let
. Let  be a bilinear functional which is continuous over compact subsets of
be a bilinear functional which is continuous over compact subsets of  . Suppose that
. Suppose that
(a) is upper semi-continuous such that each
is upper semi-continuous such that each  is compact and convex,
is compact and convex,
(b) is convex and
is convex and  is bounded,
is bounded,
(c) is an
is an  -quasi-pseudo-monotone type II
-quasi-pseudo-monotone type II  resp., strongly
resp., strongly  -quasi-pseudo-monotone type II
-quasi-pseudo-monotone type II operator and is upper semi-continuous such that each
operator and is upper semi-continuous such that each  is compact
is compact  resp., weakly compact
resp., weakly compact and convex and
and convex and  is strongly bounded,
is strongly bounded,
(d) is an upper semi-continuous mapping such that each
is an upper semi-continuous mapping such that each  is weakly compact and convex,
is weakly compact and convex,
(e)the set  is open in
is open in  .
.
Suppose further that there exist a nonempty closed and compact  resp., weakly closed and weakly compact
resp., weakly closed and weakly compact subset
subset  of
of  and a point
and a point  such that
such that  and
and

Then there exists a point  such that
such that
(1) ,
,
(2)there exist a point  and a point
and a point  such that
such that

Moreover, if  for all
for all  , then
, then  is not required to be locally convex, and if
is not required to be locally convex, and if  , then the continuity assumption on
, then the continuity assumption on  can be weakened to the assumption that, for any
can be weakened to the assumption that, for any  , the mapping
, the mapping  is continuous
is continuous  resp., weakly continuous
resp., weakly continuous on
on  .
.
Proof.
We need to show that there exists a point  such that
such that  and
and

Suppose the contrary. Then, for any  , either
, either  or there exists
or there exists  such that
such that

that is, for any  , either
, either  or
or  . If
. If  , then, by a separation theorem for convex sets in locally convex Hausdorff topological vector spaces, there exists
, then, by a separation theorem for convex sets in locally convex Hausdorff topological vector spaces, there exists  such that
such that

Let

and, for any  , set
, set

Then  Since each
Since each  is open in
is open in  by Lemma 1.7 and
by Lemma 1.7 and  is open in
is open in  by hypothesis,
by hypothesis,  is an open covering for
is an open covering for  . Since
. Since  is paracompact, there exists a continuous partition of unity
is paracompact, there exists a continuous partition of unity  for
for  subordinated to the covering
subordinated to the covering  (see Dugundji [22, Theorem VIII, 4.2]); that is, for any
(see Dugundji [22, Theorem VIII, 4.2]); that is, for any  ,
,  and
and  are continuous functions such that, for any
are continuous functions such that, for any  ,
,  for all
for all  and
and  for all
for all  and
and  ,
,  is locally finite and
is locally finite and  for any
for any  . Note that, for any
. Note that, for any  ,
,  is continuous on
is continuous on  (see [23, Corollary 10.1.1]). Define a mapping
(see [23, Corollary 10.1.1]). Define a mapping  by
by

Then we have the following.
-
(i)
Since
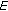 is Hausdorff, for any
is Hausdorff, for any 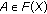 and fixed
and fixed 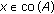 , the mapping
, the mapping  (2.10)
(2.10)
is lower semi-continuous (resp., weakly lower semi-continuous) on  by Lemma 2.1 and so the mapping
by Lemma 2.1 and so the mapping

is lower semi-continuous (resp., weakly lower semi-continuous) on  by Lemma 1.8. Also, for any fixed
by Lemma 1.8. Also, for any fixed  ,
,

is continuous on  . Hence, for any
. Hence, for any  and fixed
and fixed  , the mapping
, the mapping  is lower semi-continuous (resp., weakly lower semi-continuous) on
is lower semi-continuous (resp., weakly lower semi-continuous) on  .
.
-
(ii)
For any
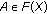 and
and 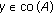 ,
, 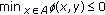 . Indeed, if this is false, then, for some
. Indeed, if this is false, then, for some  and
and 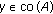 (say
(say 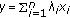 where
where  with
with 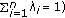 , we have
, we have  . Then, for any
. Then, for any 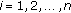 ,
, 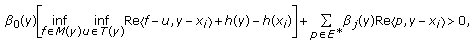 (2.13)
(2.13)
which implies that

which is a contradiction.
-
(iii)
Suppose that
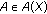 ,
, 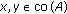 , and
, and 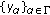 is a net in
is a net in 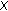 converging to
converging to 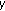 (resp., weakly to
(resp., weakly to 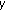 ) with
) with 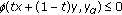 for all
for all 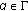 and
and 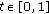 .
.
Case 1 ( ).
).
Note that  for any
for any  and
and  . Since
. Since  is strongly bounded and
is strongly bounded and  is a bounded net, it follows that
is a bounded net, it follows that

Also, we have

Thus, from (2.15), it follows that

When  , we have
, we have  for all
for all  , that is,
, that is,

Therefore, by (2.18), we have

which implies that

Hence, by (2.17) and (2.20), we have  .
.
Case 2 ( ).
).
Since  , there exists
, there exists  such that
such that  for any
for any  . When
. When  , we have
, we have  for all
for all  , that is,
, that is,

Thus it follows that

Hence, by (2.22), we have

Since  , we have
, we have

Since  for all
for all  , it follows that
, it follows that

Since  , by (2.24) and (2.25), we have
, by (2.24) and (2.25), we have

Since  is an
is an  -quasi-pseudo-monotone type II (resp., strongly
-quasi-pseudo-monotone type II (resp., strongly  -quasi-pseudo-monotone type (II) operator, we have
-quasi-pseudo-monotone type (II) operator, we have

Since  , we have
, we have

and so

When  , we have
, we have  for all
for all  , that is,
, that is,

and so, by (2.29),

Hence we have  .
.
-
(iv)
By the hypothesis, there exists a nonempty compact and so a closed (resp., weakly closed and weakly compact) subset
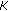 of
of 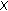 and a point
and a point 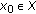 such that
such that 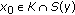 and
and 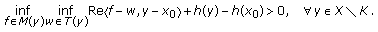 (2.32)
(2.32)
Thus it follows that

whenever  and
and  whenever
whenever  for all
for all  . Consequently, we have
. Consequently, we have

(If  is a strongly
is a strongly  -quasi-pseudo-monotone type II operator, then we equip
-quasi-pseudo-monotone type II operator, then we equip  with the weak topology.) Thus
with the weak topology.) Thus  satisfies all the hypotheses of Theorem 1.6 and so, by Theorem 1.6, there exists a point
satisfies all the hypotheses of Theorem 1.6 and so, by Theorem 1.6, there exists a point  such that
such that  for all
for all  , that is,
, that is,

Now, the rest of the proof is similar to the proof in Step 1 of Theorem 1 in [24]. Hence we have shown that

Then, by applying Theorem 1.9 as we proved in Step 3 of Theorem 1 in [24], we can show that there exist a point  and a point
and a point  such that
such that

We observe from the above proof that the requirement that  is locally convex is needed if and only if the separation theorem is applied to the case
is locally convex is needed if and only if the separation theorem is applied to the case  . Thus, if
. Thus, if  is the constant mapping
is the constant mapping  for all
for all  , the
, the  is not required to be locally convex.
is not required to be locally convex.
Finally, if  , in order to show that, for any
, in order to show that, for any  ,
,  is lower semi-continuous (resp., weakly lower semi-continuous), Lemma 2.1 is no longer needed and the weaker continuity assumption on
is lower semi-continuous (resp., weakly lower semi-continuous), Lemma 2.1 is no longer needed and the weaker continuity assumption on  that, for any
that, for any  , the mapping
, the mapping  is continuous (resp., weakly continuous) on
is continuous (resp., weakly continuous) on  is sufficient. This completes the proof.
is sufficient. This completes the proof.
We will now establish our last result of this section.
Theorem 2.3.
Let  be a locally convex Hausdorff topological vector space over
be a locally convex Hausdorff topological vector space over  , let
, let  be a nonempty paracompact convex and bounded subset of
be a nonempty paracompact convex and bounded subset of  , and let
, and let  be a vector space over
be a vector space over  . Let
. Let  be a bilinear functional such that
be a bilinear functional such that  separates points in
separates points in  ,
,  is continuous over compact subsets of
is continuous over compact subsets of  , and, for any
, and, for any  , the mapping
, the mapping  is continuous on
is continuous on  . Suppose that
. Suppose that  equips with the strong topology
equips with the strong topology  and
and
(a) is a continuous mapping such that each
is a continuous mapping such that each  is compact and convex,
is compact and convex,
(b) is convex and
is convex and  is bounded,
is bounded,
(c) is an
is an  -quasi-pseudo-monotone type II
-quasi-pseudo-monotone type II  resp., strongly
resp., strongly  -quasi-pseudo-monotone type II
-quasi-pseudo-monotone type II operator and is an upper semi-continuous mapping such that each
operator and is an upper semi-continuous mapping such that each  is strongly, that is,
is strongly, that is,  -compact and convex
-compact and convex  resp., weakly, i.e.,
resp., weakly, i.e.,  -compact and convex
-compact and convex ,
,
(d) is an upper semi-continuous mapping such that each
is an upper semi-continuous mapping such that each  is
is  -compact convex and, for any
-compact convex and, for any  ,
,  is upper semi-continuous at some point
is upper semi-continuous at some point  in
in  with
with  , where
, where

Suppose further that there exist a nonempty closed and compact  resp., weakly closed and weakly compact
resp., weakly closed and weakly compact subset
subset  of
of  and a point
and a point  such that
such that  and
and

Then there exists a point  such that
such that
(1) ,
,
(2)there exist a point  and a point
and a point  with
with

Moreover, if  for all
for all  , then
, then  is not required to be locally convex.
is not required to be locally convex.
Proof.
The proof is similar to the proof of Theorem 2 in [24] and so the proof is omitted here.
Remark 2.4.
( ) Theorems 2.2 and 2.3 of this paper are generalizations of Theorems 3.2 and 3.3 in [3], respectively, on noncompact sets. In Theorems 2.2 and 2.3,
) Theorems 2.2 and 2.3 of this paper are generalizations of Theorems 3.2 and 3.3 in [3], respectively, on noncompact sets. In Theorems 2.2 and 2.3,  is considered to be a paracompact convex and bounded subset of locally convex Hausdorff topological vector space
is considered to be a paracompact convex and bounded subset of locally convex Hausdorff topological vector space  whereas, in [3],
whereas, in [3],  is just a compact and convex subset of
is just a compact and convex subset of  . Hence our results generalize the corresponding results in [3].
. Hence our results generalize the corresponding results in [3].
( ) The first paper on generalized bi-quasi-variational inequalities was written by Shih and Tan in 1989 in [1] and the results were obtained on compact sets where the set-valued mappings were either lower semi-continuous or upper semi-continuous. Our present paper is another extension of the original work in [1] using quasi-pseudo-monotone type II operators on noncompact sets.
) The first paper on generalized bi-quasi-variational inequalities was written by Shih and Tan in 1989 in [1] and the results were obtained on compact sets where the set-valued mappings were either lower semi-continuous or upper semi-continuous. Our present paper is another extension of the original work in [1] using quasi-pseudo-monotone type II operators on noncompact sets.
-
(3)
The results in [4] were obtained on compact sets where one of the set-valued mappings is a quasi-pseudo-monotone type I operators which were defined first in [4] and extends the results in [1]. The quasi-pseudo-monotone type I operators are generalizations of pseudo-monotone type I operators introduced first in [17]. In all our results on generalized bi-quasi-variational inequalities, if the operators
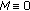 and the operators
and the operators 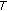 are replaced by
are replaced by 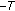 , then we obtain results on generalized quasi-variational inequalities which generalize the corresponding results in the literature (see [18]).
, then we obtain results on generalized quasi-variational inequalities which generalize the corresponding results in the literature (see [18]).
( ) The results on generalized bi-quasi-variational inequalities given in [5] were obtained for set-valued quasi-semi-monotone and bi-quasi-semi-monotone operators and the corresponding results in [2] were obtained for set-valued upper-hemi-continuous operators introduced in [6]. Our results in this paper are also further extensions of the corresponding results in [2, 5] using set-valued quasi-pseudo-monotone type II operators on noncompact sets.
) The results on generalized bi-quasi-variational inequalities given in [5] were obtained for set-valued quasi-semi-monotone and bi-quasi-semi-monotone operators and the corresponding results in [2] were obtained for set-valued upper-hemi-continuous operators introduced in [6]. Our results in this paper are also further extensions of the corresponding results in [2, 5] using set-valued quasi-pseudo-monotone type II operators on noncompact sets.
References
Shih M-H, Tan K-K: Generalized bi-quasi-variational inequalities. Journal of Mathematical Analysis and Applications 1989, 143(1):66–85. 10.1016/0022-247X(89)90029-2
Chowdhury MSR: Generalized bi-quasi-variational inequalities for upper hemi-continuous operators in non-compact settings. Acta Mathematica Hungarica 2001, 92(1–2):111–120.
Chowdhury MSR, Tan K-K: Generalized bi-quasi-variational inequalities for quasi-pseudo-monotone type II operators on compact sets. Central European Journal of Mathematics 2010, 8(1):158–169. 10.2478/s11533-009-0066-8
Chowdhury MSR, Tan K-K: Generalized bi-quasi-variational inequalities for quasi-pseudo-monotone type I operators on compact sets. Positivity 2008, 12(3):511–523. 10.1007/s11117-007-2141-3
Chowdhury MSR, Tarafdar E: Generalized bi-quasi-variational inequalities for quasi-semi-monotone and bi-quasi-monotone operators with applications in non-compact settings and minimization problems. Journal of Inequalities and Applications 2000, 5(1):63–89. 10.1155/S1025583400000059
Chowdhury MSR, Tan K-K: Generalized variational inequalities for quasi-monotone operators and applications. Bulletin of the Polish Academy of Sciences 1997, 45(1):25–54.
Chowdhury MSR, Tan K-K: Generalized variational-like inequalities for pseudo-monotone type III operators. Central European Journal of Mathematics 2008, 6(4):526–536. 10.2478/s11533-008-0049-1
Chowdhury MSR, Tan K-K: Study of generalized quasi-variational inequalities for lower and upper hemi-continuous operators on non-compact sets. Mathematical Inequalities & Applications 1999, 2(1):121–134.
Chowdhury MSR, Tan K-K: Applications of pseudo-monotone operators with some kind of upper semicontinuity in generalized quasi-variational inequalities on non-compact sets. Proceedings of the American Mathematical Society 1998, 126(10):2957–2968. 10.1090/S0002-9939-98-04436-0
Chowdhury MSR, Tan K-K: Generalized quasi-variational inequalities for upper semi-continuous operators on non-compact sets. Nonlinear Analysis: Theory, Methods & Applications 1997, 30(8):5389–5394. 10.1016/S0362-546X(97)00387-8
Chowdhury MSR, Tan K-K: Note on generalized bi-quasi-variational inequalities. Applied Mathematics Letters 1996, 9(3):97–102. 10.1016/0893-9659(96)00039-0
Tarafdar EU, Chowdhury MSR: Topological Methods for Set-Valued Nonlinear Analysis. World Scientific, Hackensack, NJ, USA; 2008:xiv+612.
Chowdhury MSR, Tarafdar E: Existence theorems of generalized quasi-variational inequalities with upper hemi-continuous and demi operators on non-compact sets. Mathematical Inequalities & Applications 1999, 2(4):585–597.
Chowdhury MSR, Tarafdar E, Thompson HB: Non-compact generalized variational inequalities for quasi-monotone and hemi-continuous operators with applications. Acta Mathematica Hungarica 2003, 99(1–2):105–122.
Chowdhury MSR, Thompson HB: Generalized variational-like inequalities for pseudomonotone type II operators. Nonlinear Analysis: Theory, Methods & Applications 2005, 63(5–7):e321-e330.
Fan K: A minimax inequality and applications. In Inequalities, III. Edited by: Shisha O. Academic Press, New York, NY, USA; 1972:103–113.
Chowdhury MSR, Tan K-K: Generalization of Ky Fan's minimax inequality with applications to generalized variational inequalities for pseudo-monotone operators and fixed point theorems. Journal of Mathematical Analysis and Applications 1996, 204(3):910–929. 10.1006/jmaa.1996.0476
Shih MH, Tan K-K: Generalized quasivariational inequalities in locally convex topological vector spaces. Journal of Mathematical Analysis and Applications 1985, 108(2):333–343. 10.1016/0022-247X(85)90029-0
Takahashi W: Nonlinear variational inequalities and fixed point theorems. Journal of the Mathematical Society of Japan 1976, 28(1):168–181. 10.2969/jmsj/02810168
Aubin J-P: Applied Functional Analysis. John Wiley & Sons, New York, NY, USA; 1979:xv+423.
Kneser H: Sur un théorème fondamental de la théorie des jeux. Comptes Rendus de l'Académie des Sciences 1952, 234: 2418–2420.
Dugundji J: Topology. Allyn and Bacon, Inc., Boston, Mass, USA; 1966:xvi+447.
Rockafellar RT: Convex Analysis, Princeton Mathematical Series, no. 28. Princeton University Press, Princeton, NJ, USA; 1970:xviii+451.
Chowdhury MSR, Tan K-K: Application of upper hemi-continuous operators on generalized bi-quasi-variational inequalities in locally convex topological vector spaces. Positivity 1999, 3(4):333–344. 10.1023/A:1009849400516
Acknowledgment
This work was supported by the Korea Research Foundation Grant funded by the Korean Government (KRF-2008-313-C00050).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chowdhury, M., Cho, Y. Generalized Bi-Quasivariational Inequalities for Quasi-Pseudomonotone Type II Operators on Noncompact Sets. J Inequal Appl 2010, 237191 (2010). https://doi.org/10.1155/2010/237191
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/237191
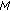 is lower semi-continuous, consider
is lower semi-continuous, consider 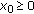 . Then
. Then 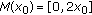 . Let
. Let 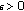 be given. Then, if
be given. Then, if 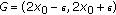 , then
, then 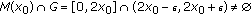 . Let
. Let 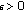 be so chosen that
be so chosen that 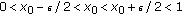 . Now, if we take
. Now, if we take 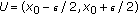 , then, for all
, then, for all 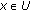 , we have
, we have  . Thus
. Thus  . Hence
. Hence 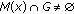 .
.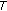 is upper semi-continuous, let
is upper semi-continuous, let 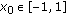 be such that
be such that  . Then
. Then 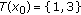 . Let
. Let 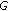 be an open set in
be an open set in 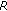 such that
such that  . Let
. Let  be such that
be such that 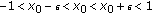 . Consider
. Consider 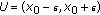 . Then, for all
. Then, for all 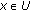 ,
, 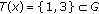 since
since 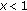 . Again, if
. Again, if 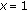 , then
, then 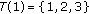 . Let
. Let 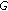 be an open set in
be an open set in 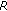 such that
such that 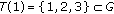 . Let
. Let 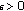 be such that
be such that 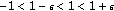 . Let
. Let 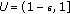 which is an open neighbourhood of
which is an open neighbourhood of 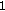 in
in 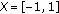 . Then for all
. Then for all 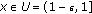 , we have
, we have 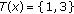 if
if 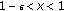 and
and 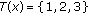 if
if 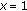 . Now,
. Now, 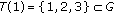 . Also, for all
. Also, for all 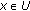 with
with 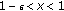 , we have
, we have 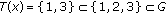 . Hence
. Hence 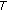 is upper semi-continuous on
is upper semi-continuous on 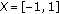 .
. is also a quasi-pseudo-monotone type II operator. To show this, let us assume first that
is also a quasi-pseudo-monotone type II operator. To show this, let us assume first that 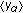 is a net in
is a net in 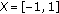 such that
such that 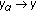 in
in 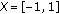 . We now show that
. We now show that 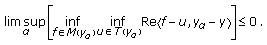
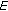 is Hausdorff, for any
is Hausdorff, for any 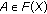 and fixed
and fixed 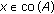 , the mapping
, the mapping 
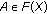 and
and 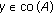 ,
, 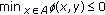 . Indeed, if this is false, then, for some
. Indeed, if this is false, then, for some  and
and 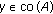 (say
(say 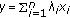 where
where  with
with 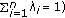 , we have
, we have  . Then, for any
. Then, for any 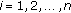 ,
, 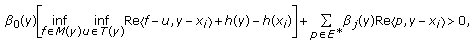
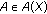 ,
, 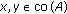 , and
, and 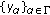 is a net in
is a net in 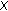 converging to
converging to 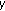 (resp., weakly to
(resp., weakly to 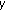 ) with
) with 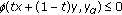 for all
for all 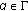 and
and 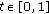 .
.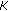 of
of 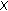 and a point
and a point 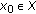 such that
such that 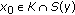 and
and 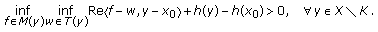
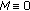 and the operators
and the operators 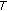 are replaced by
are replaced by 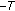 , then we obtain results on generalized quasi-variational inequalities which generalize the corresponding results in the literature (see [
, then we obtain results on generalized quasi-variational inequalities which generalize the corresponding results in the literature (see [