- Research Article
- Open access
- Published:
Applications of Wirtinger Inequalities on the Distribution of Zeros of the Riemann Zeta-Function
Journal of Inequalities and Applications volume 2010, Article number: 215416 (2011)
Abstract
On the hypothesis that the  th moments of the Hardy
th moments of the Hardy  -function are correctly predicted by random matrix theory and the moments of the derivative of
-function are correctly predicted by random matrix theory and the moments of the derivative of  are correctly predicted by the derivative of the characteristic polynomials of unitary matrices, we establish new large spaces between the zeros of the Riemann zeta-function by employing some Wirtinger-type inequalities. In particular, it is obtained that
are correctly predicted by the derivative of the characteristic polynomials of unitary matrices, we establish new large spaces between the zeros of the Riemann zeta-function by employing some Wirtinger-type inequalities. In particular, it is obtained that  which means that consecutive nontrivial zeros often differ by at least 6.1392 times the average spacing.
which means that consecutive nontrivial zeros often differ by at least 6.1392 times the average spacing.
1. Introduction
The Riemann zeta-function is defined by

and by analytic continuation elsewhere except for a simple pole at  . The identity between the Dirichlet series and the Euler product (taken over all prime numbers
. The identity between the Dirichlet series and the Euler product (taken over all prime numbers  ) is an analytic version of the unique prime factorization in the ring of integers and reflects the importance of the zeta-function for number theory. The functional equation
) is an analytic version of the unique prime factorization in the ring of integers and reflects the importance of the zeta-function for number theory. The functional equation

implies the existence of so-called trivial zeros of  at
at  for any positive integer
for any positive integer  ; all other zeros are said to be nontrivial and lie inside the so-called critical strip
; all other zeros are said to be nontrivial and lie inside the so-called critical strip  . The number
. The number  of nontrivial zeros of
of nontrivial zeros of  with ordinates in the interval
with ordinates in the interval  ,
, is asymptotically given by the Riemann-von Mangoldt formula (see [1])
is asymptotically given by the Riemann-von Mangoldt formula (see [1])

Consequently, the frequency of their appearance is increasing and the distances between their ordinates is tending to zero as  .
.
The Riemann zeta-function is one of the most studied transcendental functions, having in view its many applications in number theory, algebra, complex analysis, and statistics as well as in physics. Another reason why this function has drawn so much attention is the celebrated Riemann conjecture regarding nontrivial zeros which states that all nontrivial zeros of the Riemann zeta-function  lie on the critical line
lie on the critical line  . The distribution of zeros of
. The distribution of zeros of  is of great importance in number theory. In fact any progress in the study of the distribution of zeros of this function helps to investigate the magnitude of the largest gap between consecutive primes below a given bound. Clearly, there are no zeros in the half plane of convergence
is of great importance in number theory. In fact any progress in the study of the distribution of zeros of this function helps to investigate the magnitude of the largest gap between consecutive primes below a given bound. Clearly, there are no zeros in the half plane of convergence  , and it is also known that
, and it is also known that  does not vanish on the line
does not vanish on the line  . In the negative half plane,
. In the negative half plane,  and its derivative are oscillatory and from the functional equation there exist so-called trivial (real) zeros at
and its derivative are oscillatory and from the functional equation there exist so-called trivial (real) zeros at  for any positive integer
for any positive integer  (corresponding to the poles of the appearing Gamma-factors), and all nontrivial (nonreal) zeros are distributed symmetrically with respect to the critical line
(corresponding to the poles of the appearing Gamma-factors), and all nontrivial (nonreal) zeros are distributed symmetrically with respect to the critical line  and the real axis.
and the real axis.
There are three directions regarding the studies of the zeros of the Riemann zeta-function. The first direction is concerned with the existence of simple zeros. It is conjectured that all or at least almost all zeros of the zeta-function are simple. For this direction, we refer to the papers by Conrey [2] and Cheer and Goldston [3].
The second direction is the most important goal of number theorists which is the determination of the moments of the Riemann zeta-function on the critical line. It is important because it can be used to estimate the maximal order of the zeta-function on the critical line, and because of its applicability in studying the distribution of prime numbers and divisor problems. For more details of the second direction, we refer the reader to the papers in [4–6] and the references cited therein. For further classical results from zeta-function theory, we refer to the monograph [7] of Ivić and the papers by Kim [8–11].
For completeness in the following we give a brief summary of some of these results in this direction that we will use in the proof of the main results. It is known that the behavior of  on the critical line is reflected by the Hardy
on the critical line is reflected by the Hardy  -function
-function  as a function of a real variable, defined by
as a function of a real variable, defined by

It follows from the functional equation (1.2) that  is an infinitely often differentiable function which is real for real
is an infinitely often differentiable function which is real for real  and moreover
and moreover  . Consequently, the zeros of
. Consequently, the zeros of  correspond to the zeros of the Riemann zeta-function on the critical line. An important problem in analytic number theory is to gain an understanding of the moments of the Hardy
correspond to the zeros of the Riemann zeta-function on the critical line. An important problem in analytic number theory is to gain an understanding of the moments of the Hardy  -function
-function  function
function  and the moments of its derivative
and the moments of its derivative  which are defined by
which are defined by

For positive real numbers  , it is believed that
, it is believed that

for positive constants  and
and  will be defined later.
will be defined later.
Keating and Snaith [12] based on considerations from random matrix theory conjectured that

where

where  is the Barnes
is the Barnes  -function (for the definition of the Barnes
-function (for the definition of the Barnes  -function and its properties, we refer to [5]).
-function and its properties, we refer to [5]).
Hughes [5] used the Random Matrix Theory (RMT) and stated an interesting conjecture on the moments of the Hardy  -function and its derivatives at its zeros subject to the truth of Riemann's hypothesis when the zeros are simple. This conjecture includes for fixed
-function and its derivatives at its zeros subject to the truth of Riemann's hypothesis when the zeros are simple. This conjecture includes for fixed  the asymptotic formula of the moments of the form
the asymptotic formula of the moments of the form

where  is defined as in (1.8) and the product is over the primes. Hughes [5] was able to establish the explicit formula
is defined as in (1.8) and the product is over the primes. Hughes [5] was able to establish the explicit formula

in the range  , where
, where  is an explicit rational function of
is an explicit rational function of  for each fixed
for each fixed  . The functions
. The functions  as introduced by Hughes [5] are given in the following:
as introduced by Hughes [5] are given in the following:

where  , This sequence is continuous, and it is believed that both the nominator and denominator are monic polynomials in
, This sequence is continuous, and it is believed that both the nominator and denominator are monic polynomials in  . Using (1.10) and the definitions of the functions
. Using (1.10) and the definitions of the functions  , we can obtain the values of
, we can obtain the values of  for
for  . As indicated in [13] Hughes [5] evaluated the first four functions and then writes a numerical experiment suggesting the next three. The values of
. As indicated in [13] Hughes [5] evaluated the first four functions and then writes a numerical experiment suggesting the next three. The values of  for
for  have been collected in [6]. To the best of my knowledge there is no explicit formula to find the values of the function
have been collected in [6]. To the best of my knowledge there is no explicit formula to find the values of the function  for
for  . This limitation of the values of
. This limitation of the values of  leads to the limitation of the values of the lower bound between the zeros of the Riemann zeta-function by applying the moments (1.9). To overcame this restriction, we will use a different explicit formula of the moments to establish new values of the distance between zeros.
leads to the limitation of the values of the lower bound between the zeros of the Riemann zeta-function by applying the moments (1.9). To overcame this restriction, we will use a different explicit formula of the moments to establish new values of the distance between zeros.
Conrey et al. [4] established the moments of the derivative, on the unit circle, of characteristic polynomials of random unitary matrices and used this to formulate a conjecture for the moments of the derivative of the Riemann zeta-function on the critical line. Their method depends on the fact that the distribution of the eigenvalues of unitary matrices gives insight into the distribution of zeros of the Riemann zeta-function and the values of the characteristic polynomials of the unitary matrices give a model for the value distribution of the Riemann zeta-function. Their formulae are expressed in terms of a determinant of a matrix whose entries involve the  -Bessel function and, alternately, by a combinatorial sum. They conjectured that
-Bessel function and, alternately, by a combinatorial sum. They conjectured that

where  is the arithmetic factor and defined as in (1.8) and
is the arithmetic factor and defined as in (1.8) and

where

and  denotes the set of partitions
denotes the set of partitions  of
of  into nonnegative parts. They also gave some explicit values of
into nonnegative parts. They also gave some explicit values of  for
for  . These values will be presented in Section 2 and will be used to establish the main results in this paper.
. These values will be presented in Section 2 and will be used to establish the main results in this paper.
The third direction in the studies of the zeros of the Riemann zeta-function is the gaps between the zeros (finding small gaps and large gaps between the zeros) on the critical line when the Riemann hypothesis is satisfied. In the present paper we are concerned with the largest gaps between the zeros on the critical line assuming that the Riemann hypothesis is true.
Assuming the truth of the Riemann hypothesis Montgomery [14] studied the distribution of pairs of nontrivial zeros  and
and  and conjectured, for fixed α,
and conjectured, for fixed α, satisfying
satisfying  , that
, that

This so-called pair correlation conjecture plays a complementary role to the Riemann hypothesis. This conjecture implies the essential simplicity hypothesis that almost all zeros of the zeta-function are simple. On the other hand, the integral on the right hand side is the same as the one observed in the two-point correlation of the eigenvalues which are the energy levels of the corresponding Hamiltonian which are usually not known with uncertainty. This observation is due to Dyson and it restored some hope in an old idea of Hilbert and Polya that the Riemann hypothesis follows from the existence of a self-adjoint Hermitian operator whose spectrum of eigenvalues correspond to the set of nontrivial zeros of the zeta-function.
Now, we assume that  are the zeros of
are the zeros of  in the upper half-plane (arranged in nondecreasing order and counted according multiplicity) and
in the upper half-plane (arranged in nondecreasing order and counted according multiplicity) and  are consecutive ordinates of all zeros and define
are consecutive ordinates of all zeros and define

and set

These numbers have received a great deal of attention. In fact, important results concerning the values of them have been obtained by some authors. It is generally believed that  and
and  . Selberg [15] proved that
. Selberg [15] proved that

and the average of  is 1. Note that
is 1. Note that  is the average spacing between zeros. Fujii [16] also showed that there exist constants
is the average spacing between zeros. Fujii [16] also showed that there exist constants  and
and  such that
such that

for a positive proportion of  . Mueller [17] obtained
. Mueller [17] obtained

assuming the Riemann hypothesis. Montgomery and Odlyzko [18] showed, assuming the Riemann hypothesis, that

Conrey et al. [19] improved the bounds in (1.21) and showed that, if the Riemann hypothesis is true, then

Conrey et al. [20] obtained a new lower bound and proved that

assuming the generalized Riemann hypothesis for the zeros of the Dirichlet  -functions. Bui et al. [21] improved (1.23) and obtained
-functions. Bui et al. [21] improved (1.23) and obtained

assuming the Riemann hypothesis. Ng in [22] improved (1.24) and proved that

assuming the generalized Riemann hypothesis for the zeros of the Dirichlet  -functions.
-functions.
Hall in [23] (see also Hall [24]) assumed that  is the sequence of distinct positive zeros of the Riemann zeta-function
is the sequence of distinct positive zeros of the Riemann zeta-function  arranged in nondecreasing order and counted according multiplicity and defined the quantity
arranged in nondecreasing order and counted according multiplicity and defined the quantity

and showed that  , and the lower bound for
, and the lower bound for  bear direct comparison with such bounds for
bear direct comparison with such bounds for  dependent on the Riemann hypothesis, since if this were true the distinction between
dependent on the Riemann hypothesis, since if this were true the distinction between  and
and  would be nugatory. Of course
would be nugatory. Of course  and the equality holds if the Riemann hypothesis is true. Hall [23] used a Wirtinger-type inequality of Beesack and proved that
and the equality holds if the Riemann hypothesis is true. Hall [23] used a Wirtinger-type inequality of Beesack and proved that

In [25] Hall proved a Wirtinger inequality and used the moment

due to Ingham [26], and the moments

due to Conrey [27], and obtained

Hall [24] proved a new generalized Wirtinger-type inequality by using the calculus of variation and obtained a new value of  which is given by
which is given by

Hall [28] employed the generalized Wirtinger inequality obtained in [24], simplified the calculus used in [24] and converted the problem into one of the classical theory of equations involving Jacobi-Schur functions. Assuming that the moments in (1.9) are correctly predicted by RMT, Hall [28] proved that

In [29] the authors applied a technique involving the comparison of the continuous global average with local average obtained from the discrete average to a problem of gaps between the zeros of zeta-function assuming the Riemann hypothesis. Using this approach, which takes only zeros on the critical line into account, the authors computed similar bounds under assumption of the Riemann hypothesis when (1.9) holds. They then showed that for fixed positive integer 

holds for any  for more than
for more than  proportion of the zeros
proportion of the zeros  with a computable constant
with a computable constant  .
.
Hall [13] developed the technique used in [28] and proved that

The improvement of this value as obtained in [13] is given by

In this paper, first we apply some well-known Wirtinger-type inequalities and the moments of the Hardy  -function and the moments of its derivative to establish some explicit formulas for
-function and the moments of its derivative to establish some explicit formulas for  . Using the values of
. Using the values of  and
and  , we establish some lower bounds for
, we establish some lower bounds for  which improves the last value of
which improves the last value of  . In particular it is obtained that
. In particular it is obtained that  which means that consecutive nontrivial zeros often differ by at least 6.1392 times the average spacing. To the best of the author knowledge the last value obtained for
which means that consecutive nontrivial zeros often differ by at least 6.1392 times the average spacing. To the best of the author knowledge the last value obtained for  in the literature is the value obtained by Hall in (1.35) and nothing is known regarding
in the literature is the value obtained by Hall in (1.35) and nothing is known regarding  for
for  .
.
2. Main Results
In this section, we establish some explicit formulas for  and by using the same explicit values of
and by using the same explicit values of  and
and  we establish new lower bounds for
we establish new lower bounds for  . The explicit values of
. The explicit values of  using the formula
using the formula

are calculated in the following for  :
:

The explicit values of the parameter  that has been determined by Conrey et al. [4] for
that has been determined by Conrey et al. [4] for  are given in the following:
are given in the following:

Now, we are in a position to prove our first results in this section which gives an explicit formula of the gaps between the zeros of the Riemann zeta-function. This will be proved by applying an inequality due to Agarwal and Pang [30].
Theorem 2.1.
Assuming the Riemann hypothesis, one has

Proof.
To prove this theorem, we employ the inequality

with  and
and  , that has been proved by Agarwal and Pang [30]. As in [25] by a suitable linear transformation, we can deduce from (2.5) that if
, that has been proved by Agarwal and Pang [30]. As in [25] by a suitable linear transformation, we can deduce from (2.5) that if  and
and  , then
, then

Now, we follow the proof of [24] and supposing that  is the first zero of
is the first zero of  not less than
not less than  and
and  the last zero not greater than
the last zero not greater than  . Suppose further that for
. Suppose further that for  , we have
, we have

and apply the inequality (2.6), to obtain

Since the inequality remains true if we replace  by
by  , we have
, we have

Summing (2.9) over  , applying (1.7), (1.12) and as in [24], we obtain
, applying (1.7), (1.12) and as in [24], we obtain

whence

This implies that

and then we obtain the desired inequality (2.1). The proof is complete.
Using the values of  and
and  and (2.1) we have the new lower values for
and (2.1) we have the new lower values for  for
for  in Table 1.
in Table 1.
One can easily see that the value of  in Table 1 does not improve the lower bound in (1.35) due to Hall, but the the approach that we used is simple and depends only on a well-known Wirtinger-type inequality and the asymptotic formulas of the moments. In the following, we employ a different inequality due to Brnetić and Pečarić [31] and establish a new explicit formula for
in Table 1 does not improve the lower bound in (1.35) due to Hall, but the the approach that we used is simple and depends only on a well-known Wirtinger-type inequality and the asymptotic formulas of the moments. In the following, we employ a different inequality due to Brnetić and Pečarić [31] and establish a new explicit formula for  and then use it to find new lower bounds.
and then use it to find new lower bounds.
Theorem 2.2.
Assuming the Riemann hypothesis, one has

where  is defined by
is defined by

Proof.
To prove this theorem, we apply the inequality

that has been proved by Brnetić and Pečarić [31], where  is continuous function on
is continuous function on  with
with  . Proceeding as in the proof of Theorem 2.1 and employing (2.15), we may have
. Proceeding as in the proof of Theorem 2.1 and employing (2.15), we may have

This implies that

which is the desired inequality (2.13). The proof is complete.
To find the new lower bounds for  we need the values of
we need the values of  for
for  . These values are calculated numerically in Table 2.
. These values are calculated numerically in Table 2.
Using these values and the values of  ,
, , and the explicit formula (2.13) we have the new lower bounds for
, and the explicit formula (2.13) we have the new lower bounds for  in Table 3.
in Table 3.
We note from Table 3 that the value of  improves the value
improves the value  that has been obtained by Hall.
that has been obtained by Hall.
Finally, in the following we will employ an inequality to Beesack [32, page 59] and establish a new explicit formula for  and use it to find new values of its lower bounds.
and use it to find new values of its lower bounds.
Theorem 2.3.
Assuming the Riemann hypothesis, one has

Proof.
To prove this theorem, we apply the inequality

that has been proved by Beesack [32, page 59], where  is continuous function on
is continuous function on  with
with  . Proceeding as in Theorem 2.1 by using (2.19), we may have
. Proceeding as in Theorem 2.1 by using (2.19), we may have

This implies that

which is the desired inequity (2.18). The proof is complete.
Using these values and the values of  ,
, , and the explicit formula in (2.18) we have the new lower bounds for
, and the explicit formula in (2.18) we have the new lower bounds for  in Table 4.
in Table 4.
We note from Table 4, that the values of  for
for  are compatible with the values of
are compatible with the values of  for
for  that has been obtained by Hall [13, Table
that has been obtained by Hall [13, Table  ] and since there is no explicit value of
] and since there is no explicit value of  for
for  , to obtain the values of
, to obtain the values of  for
for  the author in [13] stopped the estimation for
the author in [13] stopped the estimation for  for
for  .
.
We notice that the calculations can be continued as above just if one knows the explicit values of  for
for  where the values
where the values

are easy to calculate. Note that the values of  that we have used in this paper are adapted from the paper by Conrey et al. [4]. It is clear that the values of
that we have used in this paper are adapted from the paper by Conrey et al. [4]. It is clear that the values of  are increasing with the increase of
are increasing with the increase of  and this may help in proving the conjecture of the distance between of the zeros of the Riemann zeta-function.
and this may help in proving the conjecture of the distance between of the zeros of the Riemann zeta-function.
References
Garunkštis R, Steuding J: Simple zeros and discrete moments of the derivative of the Riemann zeta-function. Journal of Number Theory 2005, 115(2):310–321. 10.1016/j.jnt.2004.12.006
Conrey JB: More than two fifths of the zeros of the Riemann zeta function are on the critical line. Journal für die Reine und Angewandte Mathematik 1989, 399: 1–26.
Cheer AY, Goldston DA: Simple zeros of the Riemann zeta-function. Proceedings of the American Mathematical Society 1993, 118(2):365–372. 10.1090/S0002-9939-1993-1132849-0
Conrey JB, Rubinstein MO, Snaith NC: Moments of the derivative of characteristic polynomials with an application to the Riemann zeta function. Communications in Mathematical Physics 2006, 267(3):611–629. 10.1007/s00220-006-0090-5
Hughes CPThesis, University of Bristol, Bristol, UK, 2001 Thesis, University of Bristol, Bristol, UK, 2001
Steuding J: The Riemann zeta-function and moment conjectures from random matrix theory. Mathematica Slovaca 2009, 59(3):323–338. 10.2478/s12175-009-0129-0
Ivić A: The Riemann zeta-function. John Wiley & Sons, New York, NY, USA; 1985:xvi+517.
Kim T: Euler numbers and polynomials associated with zeta functions. Abstract and Applied Analysis 2008, 2008:-11.
T. Kim, Barnes-type multiple
 -zeta functions and
-zeta functions and  -Euler polynomials, Journal of Physics, vol. 43,no. 25, 11 pages, 2010.
-Euler polynomials, Journal of Physics, vol. 43,no. 25, 11 pages, 2010.Kim T: Note on the Euler
 -zeta functions. Journal of Number Theory 2009, 129(7):1798–1804. 10.1016/j.jnt.2008.10.007
-zeta functions. Journal of Number Theory 2009, 129(7):1798–1804. 10.1016/j.jnt.2008.10.007Kim T: On
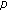 -adic interpolating function for
-adic interpolating function for 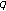 -Euler numbers and its derivatives. Journal of Mathematical Analysis and Applications 2008, 339(1):598–608. 10.1016/j.jmaa.2007.07.027
-Euler numbers and its derivatives. Journal of Mathematical Analysis and Applications 2008, 339(1):598–608. 10.1016/j.jmaa.2007.07.027Keating JP, Snaith NC: Random matrix theory and
 . Communications in Mathematical Physics 2000, 214(1):57–89. 10.1007/s002200000261
. Communications in Mathematical Physics 2000, 214(1):57–89. 10.1007/s002200000261Hall RR: Large spaces between the zeros of the Riemann zeta-function and random matrix theory. II. Journal of Number Theory 2008, 128(10):2836–2851. 10.1016/j.jnt.2007.11.011
Montgomery HL: The pair correlation of zeros of the zeta function. In Analytic Number Theory (Proceedings of Symposia in Pure Mathematics ). Volume 24. American Mathematical Society, Providence, RI, USA; 1973:181–193.
Selberg A: The zeta-function and the Riemann hypothesis. Skandinaviske Mathematiker-kongres 1946, 10: 187–200.
Fujii A: On the difference between
 consecutive ordinates of the zeros of the Riemann zeta function. Proceedings of the Japan Academy 1975, 51(10):741–743. 10.3792/pja/1195518466
consecutive ordinates of the zeros of the Riemann zeta function. Proceedings of the Japan Academy 1975, 51(10):741–743. 10.3792/pja/1195518466Mueller J: On the difference between consecutive zeros of the Riemann zeta function. Journal of Number Theory 1982, 14(3):327–331. 10.1016/0022-314X(82)90067-1
Montgomery HL, Odlyzko AM: Gaps between zeros of the zeta function. In Topics in Classical Number Theory, Vol. I, II. Volume 34. North-Holland, Amsterdam, The Netherlands; 1984:1079–1106.
Conrey JB, Ghosh A, Gonek SM: A note on gaps between zeros of the zeta function. The Bulletin of the London Mathematical Society 1984, 16(4):421–424. 10.1112/blms/16.4.421
Conrey JB, Ghosh A, Gonek SM: Large gaps between zeros of the zeta-function. Mathematika 1986, 33(2):212–238. 10.1112/S0025579300011219
Bui HM, Milinovich MB, Ng NC: A note on the gaps between consecutive zeros of the Riemann zeta-function. Proceedings of the American Mathematical Society 2010, 138(12):4167–4175. 10.1090/S0002-9939-2010-10443-4
Ng N: Large gaps between the zeros of the Riemann zeta function. Journal of Number Theory 2008, 128(3):509–556. 10.1016/j.jnt.2007.03.011
Hall RR: The behaviour of the Riemann zeta-function on the critical line. Mathematika 1999, 46(2):281–313. 10.1112/S0025579300007762
Hall RR: Generalized Wirtinger inequalities, random matrix theory, and the zeros of the Riemann zeta-function. Journal of Number Theory 2002, 97(2):397–409. 10.1016/S0022-314X(02)00005-7
Hall RR: A Wirtinger type inequality and the spacing of the zeros of the Riemann zeta-function. Journal of Number Theory 2002, 93(2):235–245. 10.1006/jnth.2001.2719
Ingham AE: Mean theorems in the theorem of the Riemann zeta-function. Proceedings London Mathematical Society 1928, 27: 273–300. 10.1112/plms/s2-27.1.273
Conrey JB: The fourth moment of derivatives of the Riemann zeta-function. The Quarterly Journal of Mathematics 1988, 39(153):21–36.
Hall RR: Large spaces between the zeros of the Riemann zeta-function and random matrix theory. Journal of Number Theory 2004, 109(2):240–265. 10.1016/j.jnt.2004.01.007
Steuding R, Steuding J: Large gaps between zeros of the zeta-function on the critical line and moment conjectures from random matrix theory. Computational Methods and Function Theory 2008, 8(1–2):121–132.
Agarwal RP, Pang PYH: Remarks on the generalizations of Opial's inequality. Journal of Mathematical Analysis and Applications 1995, 190(2):559–577. 10.1006/jmaa.1995.1091
Brnetić I, Pečarić J: Some new Opial-type inequalities. Mathematical Inequalities & Applications 1998, 1(3):385–390.
Beesack PR: Hardy's inequality and its extensions. Pacific Journal of Mathematics 1961, 11: 39–61.
Acknowledgments
The author is very grateful to the anonymous referees for valuable remarks and comments which significantly contributed to the quality of the paper. The author thanks Deanship of Scientific Research and the Research Centre in College of Science in King Saud University for encouragements and supporting this project.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Saker, S. Applications of Wirtinger Inequalities on the Distribution of Zeros of the Riemann Zeta-Function. J Inequal Appl 2010, 215416 (2011). https://doi.org/10.1155/2010/215416
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/215416
 -zeta functions and
-zeta functions and 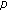 -adic interpolating function for
-adic interpolating function for 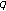 -Euler numbers and its derivatives. Journal of Mathematical Analysis and Applications 2008, 339(1):598–608. 10.1016/j.jmaa.2007.07.027
-Euler numbers and its derivatives. Journal of Mathematical Analysis and Applications 2008, 339(1):598–608. 10.1016/j.jmaa.2007.07.027 . Communications in Mathematical Physics 2000, 214(1):57–89. 10.1007/s002200000261
. Communications in Mathematical Physics 2000, 214(1):57–89. 10.1007/s002200000261 consecutive ordinates of the zeros of the Riemann zeta function. Proceedings of the Japan Academy 1975, 51(10):741–743. 10.3792/pja/1195518466
consecutive ordinates of the zeros of the Riemann zeta function. Proceedings of the Japan Academy 1975, 51(10):741–743. 10.3792/pja/1195518466