- Research Article
- Open access
- Published:
On the Stability of Generalized Quartic Mappings in Quasi-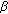 -Normed Spaces
-Normed Spaces
Journal of Inequalities and Applications volume 2010, Article number: 198098 (2010)
Abstract
We investigate the generalized Hyers-Ulam-Rassias stability problem in quasi- -normed spaces and then the stability by using a subadditive function for the generalized quartic function
-normed spaces and then the stability by using a subadditive function for the generalized quartic function  such that
such that  , where
, where  ,
,  ,
,  , for all
, for all  .
.
1. Introduction
One of the interesting questions concerning the stability problems of functional equations is as follows: when is it true that a mapping satisfying a functional equation approximately must be close to the solution of the given functional equation? Such an idea was suggested in 1940 by Ulam [1] as follows. Let be a group and let
be a group and let be a metric group with the metric
be a metric group with the metric . Given
. Given , does there exist a
, does there exist a such that if a function
such that if a function satisfies the inequality
satisfies the inequality for all
for all , then there is a homomorphism
, then there is a homomorphism with
with for all
for all ? In other words, we are looking for situations when the homomorphisms are stable; that is, if a mapping is almost a homomorphism, then there exists a true homomorphism near it. In 1941, Hyers [2] considered the case of approximately additive mappings in Banach spaces and satisfying the well-known weak Hyers inequality controlled by a positive constant. The famous Hyers stability result that appeared in [2] was generalized in the stability involving a sum of powers of norms by Aoki [3]. In 1978, Rassias [4] provided a generalization of Hyers Theorem which allows the Cauchy difference to be unbounded. During the last decades, stability problems of various functional equations have been extensively studied and generalized by a number of authors [5–10]. In particular, Rassias [11] introduced the quartic functional equation
? In other words, we are looking for situations when the homomorphisms are stable; that is, if a mapping is almost a homomorphism, then there exists a true homomorphism near it. In 1941, Hyers [2] considered the case of approximately additive mappings in Banach spaces and satisfying the well-known weak Hyers inequality controlled by a positive constant. The famous Hyers stability result that appeared in [2] was generalized in the stability involving a sum of powers of norms by Aoki [3]. In 1978, Rassias [4] provided a generalization of Hyers Theorem which allows the Cauchy difference to be unbounded. During the last decades, stability problems of various functional equations have been extensively studied and generalized by a number of authors [5–10]. In particular, Rassias [11] introduced the quartic functional equation

It is easy to see that  is a solution of (1.1) by virtue of the identity
is a solution of (1.1) by virtue of the identity

For this reason, (1.1) is called a quartic functional equation. Also Chung and Sahoo [12] determined the general solution of (1.1) without assuming any regularity conditions on the unknown function. In fact, they proved that the function  is a solution of (1.1) if and only if
is a solution of (1.1) if and only if  where the function
where the function  is symmetric and additive in each variable. Lee and Chung [13] introduced a quartic functional equation as follows:
is symmetric and additive in each variable. Lee and Chung [13] introduced a quartic functional equation as follows:

for fixed integer  with
with 
Let  be a real number with
be a real number with  and let
and let  be either
be either  or
or  We will consider the definition and some preliminary results of a quasi-
We will consider the definition and some preliminary results of a quasi- -norm on a linear space.
-norm on a linear space.
Definition 1.1.
Let  be a linear space over a field
be a linear space over a field  A quasi-
A quasi- -norm
-norm is a real-valued function on
is a real-valued function on  satisfying the followings.
satisfying the followings.
(1)  for all
for all  and
and  if and only if
if and only if 
(2)  for all
for all  and all
and all 
(3) There is a constant  such that
such that  for all
for all 
The pair  is called a quasi-
is called a quasi- -normed space if
-normed space if  is a quasi-
is a quasi- -norm on
-norm on  The smallest possible
The smallest possible  is called the modulus of concavity of
is called the modulus of concavity of  A quasi-Banach space is a complete quasi-
A quasi-Banach space is a complete quasi- -normed space.
-normed space.
A quasi- -norm
-norm  is called a
is called a  -norm (
-norm ( if
if  for all
for all  In this case, a quasi-
In this case, a quasi- -Banach space is called a
-Banach space is called a  -Banach space; see [14–16].
-Banach space; see [14–16].
In this paper, we consider the following the generalized quartic functional equation:

for fixed integers  and
and  such that
such that  for all
for all  We investigate the generalized Hyers-Ulam-Rassias stability problem in quasi-
We investigate the generalized Hyers-Ulam-Rassias stability problem in quasi- -normed spaces and then the stability by using a subadditive function for the generalized quartic function
-normed spaces and then the stability by using a subadditive function for the generalized quartic function  satisfying (1.4).
satisfying (1.4).
For the same reason as (1.1) and (1.2), we call (1.4) generalized quartic functional equation.
2. Quartic Functional Equations
Let  be real vector spaces. In this section, we will investigate that the functional equation (1.1) is equivalent to the presented functional equation (1.4).
be real vector spaces. In this section, we will investigate that the functional equation (1.1) is equivalent to the presented functional equation (1.4).
Lemma 2.1.
A mapping  satisfies the functional equation (1.1) if and only if
satisfies the functional equation (1.1) if and only if  satisfies
satisfies

where  for all
for all 
Proof.
We will show it by induction on  Assume that it holds for all less than equal
Assume that it holds for all less than equal  Now, letting
Now, letting  be
be  in (2.1),
in (2.1),

and also replacing  by
by  in (2.1),
in (2.1),

for all  Adding (2.2) and (2.3), we have
Adding (2.2) and (2.3), we have

for all  By induction steps, we have
By induction steps, we have

Hence we have

for all  Thus they are equivalent.
Thus they are equivalent.
Theorem 2.2.
If a mapping  satisfies the functional equation (1.4), then
satisfies the functional equation (1.4), then  satisfies the functional equation (2.1).
satisfies the functional equation (2.1).
Proof.
By letting  in (2.1), we have
in (2.1), we have  Since
Since  and
and 
 Putting
Putting  in (2.1),
in (2.1),

Now, replacing  by
by  in (2.7),
in (2.7),

By (2.7) and (2.8), we have  that is,
that is,  Hence
Hence  is even. This implies that
is even. This implies that  that is,
that is,  for all
for all  Now, we will show that (2.1) implies (1.4). By letting
Now, we will show that (2.1) implies (1.4). By letting  in (2.1), we have
in (2.1), we have

Switching  and
and  in the previous equation,
in the previous equation,

By (2.1) with  , the previous equation implies that
, the previous equation implies that

Hence we have

for all 
Corollary 2.3.
If a mapping  satisfies the functional equation (1.1), then
satisfies the functional equation (1.1), then  satisfies the functional equation (1.4).
satisfies the functional equation (1.4).
3. Stabilities
Throughout this section, let  be a quasi-
be a quasi- -normed space and let
-normed space and let  be a quasi-
be a quasi- -Banach space with a quasi-
-Banach space with a quasi- -norm
-norm  . Let
. Let  be the modulus of concavity of
be the modulus of concavity of  . We will investigate the generalized Hyers-Ulam-Rassias stability problem for the functional equation (1.4). After then we will study the stability by using a subadditive function. For a given mapping
. We will investigate the generalized Hyers-Ulam-Rassias stability problem for the functional equation (1.4). After then we will study the stability by using a subadditive function. For a given mapping  and all fixed integers
and all fixed integers  and
and  with
with  let
let

Theorem 3.1.
Suppose that there exists a mapping  for which a mapping
for which a mapping  satisfies
satisfies 

and the series  converges for all
converges for all  Then there exists a unique generalized quartic mapping
Then there exists a unique generalized quartic mapping  which satisfies (1.4) and the inequality
which satisfies (1.4) and the inequality

for all 
Proof.
By letting  in the inequality (3.2), since
in the inequality (3.2), since  we have
we have

that is,

for all  Now, putting
Now, putting  and multiplying
and multiplying  in the inequality (3.5), we get
in the inequality (3.5), we get

for all  Combining (3.5) and (3.6), we have
Combining (3.5) and (3.6), we have

for all  Inductively, since
Inductively, since  we have
we have

for all  For all
For all  and
and  with
with  and switching
and switching  and
and  and multiplying
and multiplying  in the inequality (3.5), inductively,
in the inequality (3.5), inductively,

for all  Since the right-hand side of the previous inequality tends to 0 as
Since the right-hand side of the previous inequality tends to 0 as  hence
hence  is a Cauchy sequence in the quasi-
is a Cauchy sequence in the quasi- -Banach space
-Banach space  Thus we may define
Thus we may define

for all  Since
Since  replacing
replacing  and
and  by
by  and
and  , respectively, and dividing by
, respectively, and dividing by  in the inequality (3.2), we have
in the inequality (3.2), we have

for all  By taking
By taking  the definition of
the definition of  implies that
implies that  satisfies (1.4) for all
satisfies (1.4) for all  that is,
that is,  is the generalized quartic mapping. Also, the inequality (3.8) implies the inequality (3.3). Now, it remains to show the uniqueness. Assume that there exists
is the generalized quartic mapping. Also, the inequality (3.8) implies the inequality (3.3). Now, it remains to show the uniqueness. Assume that there exists  satisfying (1.4) and (3.3). It is easy to show that for all
satisfying (1.4) and (3.3). It is easy to show that for all 
 and
and  as in the proof of Theorem 2.2. Then
as in the proof of Theorem 2.2. Then

for all  By letting
By letting  we immediately have the uniqueness of
we immediately have the uniqueness of  .
.
Theorem 3.2.
Suppose that there exists a mapping  for which a mapping
for which a mapping  satisfies
satisfies 

and the series  converges for all
converges for all  Then there exists a unique generalized quartic mapping
Then there exists a unique generalized quartic mapping  which satisfies (2.1) and the inequality
which satisfies (2.1) and the inequality

for all 
Proof.
If  is replaced by
is replaced by  in the inequality (3.5), then the proof follows from the proof of Theorem 3.1.
in the inequality (3.5), then the proof follows from the proof of Theorem 3.1.
Now we will recall a subadditive function and then investigate the stability under the condition that the space  is a
is a  -Banach space. The basic definitions of subadditive functions follow from [16].
-Banach space. The basic definitions of subadditive functions follow from [16].
A function  having a domain
having a domain  and a codomain
and a codomain  that are both closed under addition is called
that are both closed under addition is called
(1)a subadditive function if 
(2)a contractively subadditive function if there exists a constant  with
with  such that
such that 
(3)an expansively superadditive function if there exists a constant  with
with  such that
such that 
for all 
Theorem 3.3.
Suppose that there exists a mapping  for which a mapping
for which a mapping  satisfies
satisfies 

for all  and the map
and the map  is contractively subadditive with a constant
is contractively subadditive with a constant  such that
such that  Then there exists a unique generalized quartic mapping
Then there exists a unique generalized quartic mapping  which satisfies (1.4) and the inequality
which satisfies (1.4) and the inequality

for all 
Proof.
By the inequalities (3.5) and (3.9) of the proof of Theorem 3.1, we have

that is,

for all  and for all
and for all  and
and  with
with  Hence
Hence  is a Cauchy sequence in the space
is a Cauchy sequence in the space  Thus we may define
Thus we may define

for all  Now, we will show that the map
Now, we will show that the map  is a generalized quartic mapping. Then
is a generalized quartic mapping. Then

for all  Hence the mapping
Hence the mapping  is a generalized quartic mapping. Note that the inequality (3.18) implies the inequality (3.16) by letting
is a generalized quartic mapping. Note that the inequality (3.18) implies the inequality (3.16) by letting  and taking
and taking  Assume that there exists
Assume that there exists  satisfying (1.4) and (3.16). We know that
satisfying (1.4) and (3.16). We know that  for all
for all  Then
Then

that is,

for all  By letting
By letting  we immediately have the uniqueness of
we immediately have the uniqueness of  .
.
Theorem 3.4.
Suppose that there exists a mapping  for which a mapping
for which a mapping  satisfies
satisfies 

for all  and the map
and the map  is expansively superadditive with a constant
is expansively superadditive with a constant  such that
such that  Then there exists a unique generalized quartic mapping
Then there exists a unique generalized quartic mapping  which satisfies (1.4) and the inequality
which satisfies (1.4) and the inequality

for all 
Proof.
By letting  in (3.23), we have
in (3.23), we have

and then replacing  by
by  ,
,

for all  For all
For all  and
and  with
with  inductively we have
inductively we have

for all  The remains follow from the proof of Theorem 3.3.
The remains follow from the proof of Theorem 3.3.
References
Ulam SM: Problems in Modern Mathematics. John Wiley & Sons, New York, NY, USA; 1960.
Hyers DH: On the stability of the linear functional equation. Proceedings of the National Academy of Sciences of the United States of America 1941, 27: 222–224. 10.1073/pnas.27.4.222
Aoki T: On the stability of the linear transformation in Banach spaces. Journal of the Mathematical Society of Japan 1950, 2: 64–66. 10.2969/jmsj/00210064
Rassias ThM: On the stability of the linear mapping in Banach spaces. Proceedings of the American Mathematical Society 1978, 72(2):297–300. 10.1090/S0002-9939-1978-0507327-1
Gajda Z: On stability of additive mappings. International Journal of Mathematics and Mathematical Sciences 1991, 14(3):431–434. 10.1155/S016117129100056X
Czerwik St: On the stability of the quadratic mapping in normed spaces. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 1992, 62: 59–64. 10.1007/BF02941618
Rassias ThM: On the stability of functional equations in Banach spaces. Journal of Mathematical Analysis and Applications 2000, 251(1):264–284. 10.1006/jmaa.2000.7046
Rassias ThM, Šemrl P: On the Hyers-Ulam stability of linear mappings. Journal of Mathematical Analysis and Applications 1993, 173(2):325–338. 10.1006/jmaa.1993.1070
Rassias ThM, Shibata K: Variational problem of some quadratic functionals in complex analysis. Journal of Mathematical Analysis and Applications 1998, 228(1):234–253. 10.1006/jmaa.1998.6129
Bae J-H, Park W-G: On the generalized Hyers-Ulam-Rassias stability in Banach modules over a
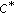 -algebra. Journal of Mathematical Analysis and Applications 2004, 294(1):196–205. 10.1016/j.jmaa.2004.02.009
-algebra. Journal of Mathematical Analysis and Applications 2004, 294(1):196–205. 10.1016/j.jmaa.2004.02.009Rassias JM: Solution of the Ulam stability problem for quartic mappings. Glasnik Matematički 1999, 34(2):243–252.
Chung JK, Sahoo PK: On the general solution of a quartic functional equation. Bulletin of the Korean Mathematical Society 2003, 40(4):565–576.
Lee Y-S, Chung S-Y: Stability of quartic functional equations in the spaces of generalized functions. Advances in Difference Equations 2009, 2009:-16.
Benyamini Y, Lindenstrauss J: Geometric Nonlinear Functional Analysis. Vol. 1, American Mathematical Society Colloquium Publications. Volume 48. American Mathematical Society, Providence, RI, USA; 2000:xii+488.
Rolewicz S: Metric Linear Spaces. 2nd edition. PWN/Polish Scientific Publishers, Warsaw, Poland; 1984:xi+459.
Rassias JM, Kim H-M: Generalized Hyers-Ulam stability for general additive functional equations in quasi-
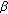 -normed spaces. Journal of Mathematical Analysis and Applications 2009, 356(1):302–309. 10.1016/j.jmaa.2009.03.005
-normed spaces. Journal of Mathematical Analysis and Applications 2009, 356(1):302–309. 10.1016/j.jmaa.2009.03.005
Acknowledgments
The author would like to thank referees for their valuable suggestions and comments. The present research was conducted by the research fund of Dankook University in 2009.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kang, D. On the Stability of Generalized Quartic Mappings in Quasi-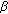 -Normed Spaces.
J Inequal Appl 2010, 198098 (2010). https://doi.org/10.1155/2010/198098
-Normed Spaces.
J Inequal Appl 2010, 198098 (2010). https://doi.org/10.1155/2010/198098
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/198098
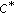 -algebra. Journal of Mathematical Analysis and Applications 2004, 294(1):196–205. 10.1016/j.jmaa.2004.02.009
-algebra. Journal of Mathematical Analysis and Applications 2004, 294(1):196–205. 10.1016/j.jmaa.2004.02.009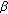 -normed spaces. Journal of Mathematical Analysis and Applications 2009, 356(1):302–309. 10.1016/j.jmaa.2009.03.005
-normed spaces. Journal of Mathematical Analysis and Applications 2009, 356(1):302–309. 10.1016/j.jmaa.2009.03.005