- Research Article
- Open access
- Published:
Stability Analysis of Recurrent Neural Networks with Random Delay and Markovian Switching
Journal of Inequalities and Applications volume 2010, Article number: 191546 (2010)
Abstract
In this paper, the exponential stability analysis problem is considered for a class of recurrent neural networks (RNNs) with random delay and Markovian switching. The evolution of the delay is modeled by a continuous-time homogeneous Markov process with a finite number of states. The main purpose of this paper is to establish easily verifiable conditions under which the random delayed recurrent neural network with Markovian switching is exponentially stable. The analysis is based on the Lyapunov-Krasovskii functional and stochastic analysis approach, and the conditions are expressed in terms of linear matrix inequalities, which can be readily checked by using some standard numerical packages such as the Matlab LMI Toolbox. A numerical example is exploited to show the usefulness of the derived LMI-based stability conditions.
1. Introduction
In recent years, the neural networks (NNs) have been extensively studied because of their immense application potentials, such as signal processing, pattern recognition, static image processing, associative memory, and combinatorial optimization. In practice, time delays are frequently encountered in dynamical systems and are often a source of oscillation and instability. Thus, the stability problem of delayed neural networks has become a topic of great theoretic and practical importance. Numerous important results have been reported for neural networks with time delays (see, e.g., [1–23]).
On the other hand, it can be seen from the existing references that only the deterministic time-delay case was concerned, and the stability criteria were derived based only on the information of variation range of the time delay. In practice, the delay in some NNs is due to multiple factors (e.g., synaptic transmission delay, neuroaxon transmission delay); one natural paradigm for treating it is to use a probabilistic description (see, e.g., [17, 18, 24, 25]). For example, to control and propagate the stochastic signals through universal learning networks (ULNs), a probabilistic universal learning network (PULN) was proposed in [25]. In a PULN, the output signal of the node is transferred to another node by multibranches with arbitrary time delay which is random and its probabilistic characteristic can often be measured by the statistical methods. For this case, if some values of the time delay are very large but the probabilities of the delay taking such large values are very small, it may result in a more conservative result if only the information of variation range of the time delay is considered. In many situations, the delay process can be modeled as a Markov process with a finite number of states (see, e.g., [26, 27]). References [26, 27] argue in favor of such representation of the delay in communication networks. The discrete values of the delay may correspond to "low", "medium", and "high" network loads.
In practice, sometimes a neural network has finite state representations (also called modes, patterns, or clusters), and the modes may switch (or jump) from one to another at different times [19–23]. Recently, it has been revealed in [19] that switching (or jumping) between different neural networks modes can be governed by a Markov chain. Specifically, the class of neural networks with Markovian switching has two components in the state vector. The first one, which carries continuously, is referred to be the continuous state of the neural networks, and the second one, which varies discretely, is referred to be the mode of the neural networks. For a specific mode, the dynamics of the neural networks is continuous, but the switchings among different modes may be seen as discrete events. It should be pointed out that neural networks with Markovian switching have been a subject of great significance in modeling a class of neural networks with finite network modes and were studied by several researchers, for example, [19–23, 28], despite their practical importance. However, to the best of the authors' knowledge, so far, the stability analysis of RNNs with random delay and Markovian switching has received little attention in the literature. This situation motivates our present investigation.
Motivated by the above discussions, the aim of this paper is to investigate the exponential stability of RNNs with random delay and Markovian switching in mean square. By using a Markov chain with a finite number of states, we propose a new model of RNNs with random delay and Markovian switching. The analysis is based on the Lyapunov-Krasovskii functional and stochastic analysis approach, and the conditions for the stability criteria are expressed in terms of linear matrix inequalities which can be readily checked by using some standard numerical packages. A simple example has been provided to demonstrate the effectiveness and applicability of the proposed testing criteria.
Notations
The notations are quite standard. Throughout this paper,  and
and  denote, respectively, the
denote, respectively, the  -dimensional Euclidean space and the set of all
-dimensional Euclidean space and the set of all  real matrices. The superscript "
real matrices. The superscript " " denotes the transpose and the notation
" denotes the transpose and the notation  (resp.,
(resp.,  ), where
), where  and
and  are symmetric matrices, means that
are symmetric matrices, means that  is positive semidefinite (resp., positive definite).
is positive semidefinite (resp., positive definite).  is the identity matrix with compatible dimension. For
is the identity matrix with compatible dimension. For  ,
,  denotes the family of continuous functions
denotes the family of continuous functions  from
from  to
to  with the norm
with the norm  , where
, where  is the Euclidean norm in
is the Euclidean norm in  . If
. If  is a matrix, denote by
is a matrix, denote by  its operator norm, that is,
its operator norm, that is,  , where
, where  (resp.,
(resp.,  ) means the largest (resp., smallest) eigenvalue of
) means the largest (resp., smallest) eigenvalue of  . Moreover, let
. Moreover, let  be complete probability space with a filtration
be complete probability space with a filtration  (i.e., it is right continuous and
(i.e., it is right continuous and  contains all P-null sets). Denote by
contains all P-null sets). Denote by  the family of all bounded,
the family of all bounded,  -measurable,
-measurable,  -valued random variables. For
-valued random variables. For  and
and  , denote by
, denote by  the family of all
the family of all  -measurable,
-measurable,  -valued random variables
-valued random variables  such that
such that  , where
, where  stands for the mathematical expectation operator with respect to the given probability measure P. In symmetric block matrices, we use an asterisk "
stands for the mathematical expectation operator with respect to the given probability measure P. In symmetric block matrices, we use an asterisk " " to represent a term that is induced by symmetry and diag
" to represent a term that is induced by symmetry and diag stands for a block-diagonal matrix. Sometimes, the arguments of a function will be omitted in the analysis when no confusion can arise.
stands for a block-diagonal matrix. Sometimes, the arguments of a function will be omitted in the analysis when no confusion can arise.
2. Problem Formulation
In this section, we will introduce the model of recurrent neural networks with random delay and Markovian switching, give the definition of stability related, and put forward the problem to be dealt with in this paper.
Let  be a right-continuous Markov process on the probability space which takes values in the finite space
be a right-continuous Markov process on the probability space which takes values in the finite space  satisfying
satisfying  and its generator
and its generator  is given by
is given by

where  and
and  ,
,  is the transition rate from
is the transition rate from  to
to  if
if  , and
, and

Consider the following recurrent neural network with constant delay model described by

where  is the states vector with the
is the states vector with the  neurons; the diagonal matrix
neurons; the diagonal matrix  has positive entries
has positive entries  ;
;  and
and  are the connection weight matrix and delayed connection weight matrix, respectively;
are the connection weight matrix and delayed connection weight matrix, respectively;  denotes the neuron activation function with
denotes the neuron activation function with  ;
;  is a constant external input vector;
is a constant external input vector;  , which may be unknown, denotes the time delay.
, which may be unknown, denotes the time delay.
Throughout this paper, we make the following assumptions.
Assumption.
For  the neuron activation functions in (2.3) satisfy
the neuron activation functions in (2.3) satisfy


for any  where
where  and
and  are positive constants.
are positive constants.
Remark 2.2.
It is obvious that the conditions in Assumption 2.1 are more general than the usual sigmoid functions and the recently commonly used Lipschitz conditions; see, for example, [3–7].
Let  be the equilibrium point of network (2.3). For the purpose of simplicity, we can shift the intended equilibrium points
be the equilibrium point of network (2.3). For the purpose of simplicity, we can shift the intended equilibrium points  to the origin. The transformation, that is,
to the origin. The transformation, that is,  , puts system (2.3) into the following form:
, puts system (2.3) into the following form:

where  is the state vector of transformed system,
is the state vector of transformed system,  , and
, and  . Obviously, Assumption 2.1 implies that
. Obviously, Assumption 2.1 implies that  satisfy the following condition:
satisfy the following condition:

and from (2.7), we have

Now we consider the following recurrent neural network with random delay and Markovian switching, which is actually a modification of (2.6):

where  is a Markov process taking values in a finite state space
is a Markov process taking values in a finite state space 
Assumption.
The neuron activation function in (2.9),  , satisfies the following condition:
, satisfies the following condition:

where  is a positive constant.
is a positive constant.
Now we will work on the network mode  for all
for all  Let
Let  denote the state trajectory from the initial data
denote the state trajectory from the initial data  on
on  in
in  . According to [26, 29], for any initial value
. According to [26, 29], for any initial value  , (2.9) has only a globally continuous state. Clearly, the network (2.9) admits an equilibrium point (trivial solution)
, (2.9) has only a globally continuous state. Clearly, the network (2.9) admits an equilibrium point (trivial solution)  corresponding to the initial data
corresponding to the initial data  .
.
Remark 2.4.
It is noted that the introduction of random delay modeled by a continuous-time homogeneous Markov process with a finite number of states was first introduced in [26, 27]. Unlike the common assumptions on the delay in the published literature, the probability distribution of the delay taking some values is assumed to be known in advance in this paper, and then a new model of the neural system (2.9) has been derived, which can be seen as an extension of the common neural system (2.6).
For convenience, each possible value of  is denoted by
is denoted by  in the sequel. Then we have
in the sequel. Then we have

where  for any
for any  are known constant matrices of appropriate dimensions.
are known constant matrices of appropriate dimensions.
The following stability concept is needed in this paper.
Definition 2.5.
For system (2.9) and every  ,
,  the trivial solution is exponentially stable in the mean-square if there exists a pair of positive constants
the trivial solution is exponentially stable in the mean-square if there exists a pair of positive constants  and
and  such that
such that

where  is the solution of system (2.9) at time
is the solution of system (2.9) at time  under the initial state
under the initial state  and initial mode
and initial mode  .
.
3. Main Results and Proofs
To establish a more general result, we need more notations. Let  denote the family of all nonnegative functions
denote the family of all nonnegative functions  on
on  , which are continuously twice differentiable in
, which are continuously twice differentiable in  and differentiable in
and differentiable in  . If
. If  , define an operator
, define an operator  from
from  to
to  by
by

where

The main result of this paper is given in the following theorem.
Theorem 3.1.
Let  be a fixed constant. Then under Assumptions 2.1 and 2.3, the recurrent neural network (2.9) with random delay and Markovian switching is exponentially stable in the mean square if there exist symmetric positive matrices
be a fixed constant. Then under Assumptions 2.1 and 2.3, the recurrent neural network (2.9) with random delay and Markovian switching is exponentially stable in the mean square if there exist symmetric positive matrices  and positive diagonal matrices
and positive diagonal matrices 
 such that the following LMIs holds
such that the following LMIs holds

Proof.
In order to establish the stability conditions, we define a Lyapunov functional candidate  by
by

It is known (see [26, 29]) that  is a
is a  -valued Markov process. From (2.9), (3.1), and (3.4), the weak infinitesimal operator
-valued Markov process. From (2.9), (3.1), and (3.4), the weak infinitesimal operator  (see [30]) of the stochastic process
(see [30]) of the stochastic process  is given by
is given by

By using (2.7), we have

It is easy to see that

Substituting (2.8), (2.10), and (3.7) into (3.5) leads to

Using the conditions of Theorem 3.1, we have

Hence

where

Moreover

Combining (3.10)–(3.12), we have

Hence

where

which implies that system (2.9) is exponentially stable in the mean square sense. The proof is completed.
4. A Numerical Example
In this section, a numerical example is presented to demonstrate the effectiveness and applicability of the developed method on the exponential stability in the mean square sense of the recurrent neural network (2.9) with random delay and Markovian switching.
Example 4.1.
Consider a two-neuron neural network (2.9) with two modes. The network parameters are given as follows:

By using the Matlab LMI toolbox [31], we solve the LMIs in Theorem 3.1 and obtain

Therefore, it follows from Theorem 3.1 that the recurrent neural network (2.9) with random delay and Markovian switching is exponentially stable in the mean square.
5. Conclusions
The analysis problem of an exponential stability in the mean square sense for a class of RNNs with random delay and Markovian switching has been studied. By utilizing a Markov chain to describe discrete delay, a new neural network model has been presented. The Lyapunov-Krasovskii stability theory and the differential rule have been employed to establish sufficient conditions for the recurrent neural network with random delay and Markovian switching to be exponentially stable. These conditions are expressed in terms of the feasibility to a set of linear matrix inequalities, and therefore the exponentially stable of the recurrent neural network with random delay and Markovian switching can be easily checked by utilizing the numerically efficient Matlab LMI toolbox. A simple example has been exploited to show the usefulness of the derived LMI-based stability conditions.
References
Arik S: Stability analysis of delayed neural networks. IEEE Transactions on Circuits and Systems I 2000, 47(7):1089–1092. 10.1109/81.855465
Civalleri PP, Gilli M, Pandolfi L: On stability of cellular neural networks with delay. IEEE Transactions on Circuits and Systems I 1993, 40(3):157–165. 10.1109/81.222796
Cao J: Global exponential stability and periodic solutions of delayed cellular neural networks. Journal of Computer and System Sciences 2000, 60(1):38–46. 10.1006/jcss.1999.1658
Zhao H: Global exponential stability and periodicity of cellular neural networks with variable delays. Physics Letters A 2005, 336(4–5):331–341. 10.1016/j.physleta.2004.12.001
Wang Z, Liu Y, Liu X: On global asymptotic stability of neural networks with discrete and distributed delays. Physics Letters A 2005, 345(4–6):299–308.
Chen T, Lu W, Chen G: Dynamical behaviors of a large class of general delayed neural networks. Neural Computation 2005, 17(4):949–968. 10.1162/0899766053429417
Lou XY, Cui B: New LMI conditions for delay-dependent asymptotic stability of delayed Hopfield neural networks. Neurocomputing 2006, 69(16–18):2374–2378.
He Y, Liu G, Rees D: New delay-dependent stability criteria for neural networks with time-varying delay. IEEE Transactions on Neural Networks 2007, 18: 310–314.
Zheng C, Lu L, Wang Z: New LMI-based delay-dependent criterion for global asymptotic stability of cellular neural networks. Neurocomputing 2009, 72: 3331–3336. 10.1016/j.neucom.2009.01.013
Liao XX, Mao X: Stability of stochastic neural networks. Neural, Parallel & Scientific Computations 1996, 4(2):205–224.
Liao XX, Mao X: Exponential stability and instability of stochastic neural networks. Stochastic Analysis and Applications 1996, 14(2):165–185. 10.1080/07362999608809432
Blythe S, Mao X, Liao X: Stability of stochastic delay neural networks. Journal of the Franklin Institute 2001, 338(4):481–495. 10.1016/S0016-0032(01)00016-3
Wan L, Sun J: Mean square exponential stability of stochastic delayed Hopfield neural networks. Physics Letters A 2005, 343(4):306–318. 10.1016/j.physleta.2005.06.024
Sun Y, Cao J:
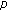 th moment exponential stability of stochastic recurrent neural networks with time-varying delays. Nonlinear Analysis: Real World Applications 2007, 8(4):1171–1185. 10.1016/j.nonrwa.2006.06.009
th moment exponential stability of stochastic recurrent neural networks with time-varying delays. Nonlinear Analysis: Real World Applications 2007, 8(4):1171–1185. 10.1016/j.nonrwa.2006.06.009Ma L, Da F: Mean-square exponential stability of stochastic Hopfield neural networks with time-varying discrete and distributed delays. Physics Letters A 2009, 373(25):2154–2161. 10.1016/j.physleta.2009.04.031
Zhang Y, Yue D, Tian E: Robust delay-distribution-dependent stability of discrete-time stochastic neural networks with time-varying delay. Neurocomputing 2009, 72(4–6):1265–1273.
Yue D, Zhang Y, Tian E, Peng C: Delay-distribution-dependent exponential stability criteria for discrete-time recurrent neural networks with stochastic delay. IEEE Transactions on Neural Networks 2008, 19(7):1299–1306.
Yang R, Gao H, Lam J, Shi P: New stability criteria for neural networks with distributed and probabilistic delays. Circuits, Systems, and Signal Processing 2009, 28(4):505–522.
Tiňo P, Čerňanský M, Beňušková L: Markovian architectural bias of recurrent neural networks. IEEE Transactions on Neural Networks 2004, 15(1):6–15. 10.1109/TNN.2003.820839
Wang Z, Liu Y, Yu L, Liu X: Exponential stability of delayed recurrent neural networks with Markovian jumping parameters. Physics Letters A 2006, 356(4–5):346–352. 10.1016/j.physleta.2006.03.078
Huang H, Ho DWC, Qu Y: Robust stability of stochastic delayed additive neural networks with Markovian switching. Neural Networks 2007, 20(7):799–809. 10.1016/j.neunet.2007.07.003
Liu Y, Wang Z, Liu X: On delay-dependent robust exponential stability of stochastic neural networks with mixed time delays and Markovian switching. Nonlinear Dynamics 2008, 54(3):199–212. 10.1007/s11071-007-9321-3
Shen Y, Wang J: Almost sure exponential stability of recurrent neural networks with Markovian switching. IEEE Transactions on Neural Networks 2009, 20(5):840–855.
Hopfield JJ: Neural networks and physical systems with emergent collective computational abilities. Proceedings of the National Academy of Sciences of the United States of America 1982, 79(8):2554–2558. 10.1073/pnas.79.8.2554
Hirasawa K, Mabu S, Hu J: Propagation and control of stochastic signals through universal learning networks. Neural Networks 2006, 19(4):487–499. 10.1016/j.neunet.2005.10.005
Kolmanovsky I, Maizenberg TL: Mean-square stability of nonlinear systems with time-varying, random delay. Stochastic Analysis and Applications 2001, 19(2):279–293. 10.1081/SAP-100001189
Kolmanovskii VB, Maizenberg TL, Richard J-P: Mean square stability of difference equations with a stochastic delay. Nonlinear Analysis: Theory, Methods &Applications 2003, 52(3):795–804. 10.1016/S0362-546X(02)00133-5
Ji Y, Chizeck HJ: Controllability, stabilizability, and continuous-time Markovian jump linear quadratic control. IEEE Transactions on Automatic Control 1990, 35(7):777–788. 10.1109/9.57016
Mao X, Yuan C: Stochastic Differential Equations with Markovian Switching. Imperial College Press, London, UK; 2006:xviii+409.
Zhu E: Stability of several classes of stochastic neural network models with Markovian switching, Doctoral dissertation. Central South University; 2007.
Boyd S, EI Ghaoui L, Feron E, Balakrishnan V: Linear Matrix Inequalities in System and Control Theory. SIAM, Philadelphia, Pa, USA; 1994.
Acknowledgments
The authors would like to thank the editor and the anonymous referees for their detailed comments and valuable suggestions which considerably improved the presentation of this paper. The authors would like to thank Prof. Fuzhou Gong for his guidance. The research is supported by the Excellent Youth Foundation of Educational Committee of Hunan Provincial (08B005), the Hunan Postdoctoral Scientific Program (2009RS3020), the National Natural Science Foundation of China (10771044), the Natural Science Foundation of Hunan Province (09JJ6006), the Scientific Research Funds of Hunan Provincial Education Department of China (09C059), and the Scientific Research Funds of Hunan Provincial Science and Technology Department of China (2009FJ3103).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhu, E., Wang, Y., Wang, Y. et al. Stability Analysis of Recurrent Neural Networks with Random Delay and Markovian Switching. J Inequal Appl 2010, 191546 (2010). https://doi.org/10.1155/2010/191546
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/191546
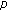 th moment exponential stability of stochastic recurrent neural networks with time-varying delays. Nonlinear Analysis: Real World Applications 2007, 8(4):1171–1185. 10.1016/j.nonrwa.2006.06.009
th moment exponential stability of stochastic recurrent neural networks with time-varying delays. Nonlinear Analysis: Real World Applications 2007, 8(4):1171–1185. 10.1016/j.nonrwa.2006.06.009