- Research Article
- Open access
- Published:
A General Iterative Process for Solving a System of Variational Inclusions in Banach Spaces
Journal of Inequalities and Applications volume 2010, Article number: 190126 (2010)
Abstract
The purpose of this paper is to introduce a general iterative method for finding solutions of a general system of variational inclusions with Lipschitzian relaxed cocoercive mappings. Strong convergence theorems are established in strictly convex and 2-uniformly smooth Banach spaces. Moreover, we apply our result to the problem of finding a common fixed point of a countable family of strict pseudo-contraction mappings.
1. Introduction
Let  . A Banach space
. A Banach space  is said to be uniformly convex if, for any
is said to be uniformly convex if, for any  , there exists
, there exists  such that, for any
such that, for any  ,
,

It is known that a uniformly convex Banach space is reflexive and strictly convex. A Banach space  is said to be smooth if the limit
is said to be smooth if the limit

exists for all  . It is also said to be uniformly smooth if the limit is attained uniformly for all
. It is also said to be uniformly smooth if the limit is attained uniformly for all  . The norm of
. The norm of  is said to be Fréchet differentiable if, for any
is said to be Fréchet differentiable if, for any  , the above limit is attained uniformly for all
, the above limit is attained uniformly for all  . The modulus of smoothness of
. The modulus of smoothness of  is defined by
is defined by

where  . It is known that
. It is known that  is uniformly smooth if and only if
is uniformly smooth if and only if  . Let
. Let  be a fixed real number with
be a fixed real number with  . A Banach space
. A Banach space  is said to be
is said to be  -uniformly smooth if there exists a constant
-uniformly smooth if there exists a constant  such that
such that  for all
for all  .
.
From [1], we know the following property.
Let  be a real number with
be a real number with  and let
and let  be a Banach space. Then
be a Banach space. Then  is
is  -uniformly smooth if and only if there exists a constant
-uniformly smooth if and only if there exists a constant  such that
such that

The best constant  in the above inequality is called the
in the above inequality is called the  -uniformly smoothness constant of
-uniformly smoothness constant of  (see [1] for more details).
(see [1] for more details).
Let  be a real Banach space and
be a real Banach space and  the dual space of
the dual space of  . Let
. Let  denote the pairing between
denote the pairing between  and
and  . For
. For  , the generalized duality mapping
, the generalized duality mapping  is defined by
is defined by

In particular,  is called the normalized duality mapping. It is known that
is called the normalized duality mapping. It is known that  for all
for all  . If
. If  is a Hilbert space, then
is a Hilbert space, then  is the identity. Note the following.
is the identity. Note the following.
(1)  is a uniformly smooth Banach space if and only if
is a uniformly smooth Banach space if and only if  is single-valued and uniformly continuous on any bounded subset of
is single-valued and uniformly continuous on any bounded subset of  .
.
(2) All Hilbert spaces,  (or
(or  ) spaces (
) spaces ( ), and the Sobolev spaces
), and the Sobolev spaces  (
( ) are
) are  -uniformly smooth, while
-uniformly smooth, while  (or
(or  ) and
) and  spaces (
spaces ( ) are
) are  -uniformly smooth.
-uniformly smooth.
(3) Typical examples of both uniformly convex and uniformly smooth Banach spaces are  , where
, where  . More precisely,
. More precisely,  is
is  -uniformly smooth for any
-uniformly smooth for any  .
.
Further, we have the following properties of the generalized duality mapping  :
:
(i) for all
for all  with
with  ,
,
(ii) for all
for all  and
and  ,
,
(iii) for all
for all  .
.
It is known that, if  is smooth, then
is smooth, then  is single valued. Recall that the duality mapping
is single valued. Recall that the duality mapping  is said to be weakly sequentially continuous if, for each sequence
is said to be weakly sequentially continuous if, for each sequence  with
with  weakly, we have
weakly, we have  weakly-
weakly- . We know that, if
. We know that, if  admits a weakly sequentially continuous duality mapping, then
admits a weakly sequentially continuous duality mapping, then  is smooth. For the details, see [2].
is smooth. For the details, see [2].
Let  be a nonempty closed convex subset of a smooth Banach space
be a nonempty closed convex subset of a smooth Banach space  . Recall the following definitions of a nonlinear mapping
. Recall the following definitions of a nonlinear mapping  , the following are mentioned.
, the following are mentioned.
Definition 1.1.
Given a mapping  .
.
(i) is said to be accretive if
is said to be accretive if

for all  .
.
(ii) is said to be
is said to be  -strongly accretive if there exists a constant
-strongly accretive if there exists a constant  such that
such that

for all  .
.
(iii) is said to be
is said to be  -inverse-strongly accretive or
-inverse-strongly accretive or  -cocoercive if there exists a constant
-cocoercive if there exists a constant  such that
such that

for all  .
.
(iv) is said to be
is said to be  -relaxed cocoercive if there exists a constant
-relaxed cocoercive if there exists a constant  such that
such that

for all  .
.
(v) is said to be
is said to be  -relaxed cocoercive if there exist positive constants
-relaxed cocoercive if there exist positive constants  and
and  such that
such that

for all  .
.
Remark 1.2.
( ) Every
) Every  -strongly accretive mapping is an accretive mapping.
-strongly accretive mapping is an accretive mapping.
( ) Every
) Every  -strongly accretive mapping is a
-strongly accretive mapping is a  -relaxed cocoercive mapping for any positive constant
-relaxed cocoercive mapping for any positive constant  but the converse is not true in general. Then the class of relaxed cocoercive operators is more general than the class of strongly accretive operators.
but the converse is not true in general. Then the class of relaxed cocoercive operators is more general than the class of strongly accretive operators.
( ) Evidently, the definition of the inverse-strongly accretive operator is based on that of the inverse-strongly monotone operator in real Hilbert spaces (see, e.g., [3]).
) Evidently, the definition of the inverse-strongly accretive operator is based on that of the inverse-strongly monotone operator in real Hilbert spaces (see, e.g., [3]).
( ) The notion of the cocoercivity is applied in several directions, especially for solving variational inequality problems using the auxiliary problem principle and projection methods [4]. Several classes of relaxed cocoercive variational inequalities have been studied in [5, 6].
) The notion of the cocoercivity is applied in several directions, especially for solving variational inequality problems using the auxiliary problem principle and projection methods [4]. Several classes of relaxed cocoercive variational inequalities have been studied in [5, 6].
Next, we consider a system of quasivariational inclusions as follows.
Find  such that
such that

where  and
and  are nonlinear mappings for each
are nonlinear mappings for each 
As special cases of problem (1.11), we have the following.
(1) If  and
and  , then problem (1.11) is reduced to the following.
, then problem (1.11) is reduced to the following.
Find  such that
such that

(2) Further, if  in problem (1.12), then problem (1.12) is reduced to the following
in problem (1.12), then problem (1.12) is reduced to the following
Find  such that
such that

In 2006, Aoyama et al. [7] considered the following problem.
Find  such that
such that

They proved that the variational inequality (1.14) is equivalent to a fixed point problem. The element  is a solution of the variational inequality (1.14) if and only if
is a solution of the variational inequality (1.14) if and only if  satisfies the following equation:
satisfies the following equation:

where  is a constant and
is a constant and  is a sunny nonexpansive retraction from
is a sunny nonexpansive retraction from  onto
onto  , see the definition below.
, see the definition below.
Let  be a subset of
be a subset of  , and
, and  be a mapping of
be a mapping of  into
into  . Then
. Then  is said to be sunny if
is said to be sunny if

whenever  for
for  and
and  . A mapping
. A mapping  of
of  into itself is called a retraction if
into itself is called a retraction if  . If a mapping
. If a mapping  of
of  into itself is a retraction, then
into itself is a retraction, then  for all
for all  , where
, where  is the range of
is the range of  . A subset
. A subset  of
of  is called a sunny nonexpansive retract of
is called a sunny nonexpansive retract of  if there exists a sunny nonexpansive retraction from
if there exists a sunny nonexpansive retraction from  onto
onto  .
.
The following results describe a characterization of sunny nonexpansive retractions on a smooth Banach space.
Proposition 1.3 (see [8]).
Let  be a smooth Banach space and
be a smooth Banach space and  a nonempty subset of
a nonempty subset of  . Let
. Let  be a retraction and
be a retraction and  the normalized duality mapping on
the normalized duality mapping on  . Then the following are equivalent:
. Then the following are equivalent:
(1)  is sunny and nonexpansive,
is sunny and nonexpansive,
(2) 
Recall that a mapping  is called contractive if there exists a constant
is called contractive if there exists a constant  such that
such that

A mapping  is said to be
is said to be  -strictly pseudocontractive if there exists a constant
-strictly pseudocontractive if there exists a constant  such that
such that

Note that the class of  -strictly pseudocontractive mappings strictly includes the class of nonexpansive mappings which are mappings
-strictly pseudocontractive mappings strictly includes the class of nonexpansive mappings which are mappings  on
on  such that
such that

for all  . That is,
. That is,  is nonexpansive if and only if
is nonexpansive if and only if  is
is  -strict pseudocontractive. We denote by
-strict pseudocontractive. We denote by  the set of fixed points of
the set of fixed points of  .
.
Proposition 1.4 (see [9]).
Let  be a nonempty closed convex subset of a uniformly convex and uniformly smooth Banach space
be a nonempty closed convex subset of a uniformly convex and uniformly smooth Banach space  and
and  a nonexpansive mapping of
a nonexpansive mapping of  into itself with
into itself with  . Then the set
. Then the set  is a sunny nonexpansive retract of
is a sunny nonexpansive retract of  .
.
Definition 1.5.
A countable family of mapping  is called a family of uniformly
is called a family of uniformly -strict pseudocontractions if there exists a constant
-strict pseudocontractions if there exists a constant  such that
such that

For the class of nonexpansive mappings, one classical way to study nonexpansive mappings is to use contractions to approximate a nonexpansive mapping [10, 11]. More precisely, take  and define a contraction
and define a contraction  by
by

where  is a fixed point and
is a fixed point and  is a nonexpansive mapping. Banach's contraction mapping principle guarantees that
is a nonexpansive mapping. Banach's contraction mapping principle guarantees that  has a unique fixed point
has a unique fixed point  in
in  ; that is,
; that is,

It is unclear, in general, what the behavior of  is as
is as  even if
even if  has a fixed point. However, in the case of
has a fixed point. However, in the case of  having a fixed point, Ceng et al. [12] proved that, if
having a fixed point, Ceng et al. [12] proved that, if  is a Hilbert space, then
is a Hilbert space, then  converges strongly to a fixed point of
converges strongly to a fixed point of  . Reich [11] extended Browder's result to the setting of Banach spaces and proved that, if
. Reich [11] extended Browder's result to the setting of Banach spaces and proved that, if  is a uniformly smooth Banach space, then
is a uniformly smooth Banach space, then  converges strongly to a fixed point of
converges strongly to a fixed point of  , and the limit defines the (unique) sunny nonexpansive retraction from
, and the limit defines the (unique) sunny nonexpansive retraction from  onto
onto  .
.
Reich [11] showed that, if  is uniformly smooth and
is uniformly smooth and  is the fixed point set of a nonexpansive mapping from
is the fixed point set of a nonexpansive mapping from  into itself, then there is a unique sunny nonexpansive retraction from
into itself, then there is a unique sunny nonexpansive retraction from  onto
onto  and it can be constructed as follows.
and it can be constructed as follows.
Proposition 1.6 (see [11]).
Let  be a uniformly smooth Banach space and
be a uniformly smooth Banach space and  a nonexpansive mapping such that
a nonexpansive mapping such that  . For each fixed
. For each fixed  and every
and every  , the unique fixed point
, the unique fixed point  of the contraction
of the contraction  converges strongly as
converges strongly as  to a fixed point of
to a fixed point of  . Define
. Define  by
by  . Then
. Then  is the unique sunny nonexpansive retract from
is the unique sunny nonexpansive retract from  onto
onto  ; that is,
; that is,  satisfies the property.
satisfies the property.

Notation 1.
We use  to denote strong convergence to
to denote strong convergence to  of the net
of the net  as
as  .
.
Definition 1.7 (see [13]).
Let  be a multivalued maximal accretive mapping. The single-valued mapping
be a multivalued maximal accretive mapping. The single-valued mapping  defined by
defined by

is called the resolvent operator associated with  , where
, where  is any positive number and
is any positive number and  is the identity mapping.
is the identity mapping.
Recently, many authors have studied the problems of finding a common element of the set of fixed points of a nonexpansive mapping and one of the sets of solutions to the variational inequalities (1.11)–(1.14) by using different iterative methods (see, e.g., [7, 14–16]).
Very recently, Qin et al. [16] considered the problem of finding the solutions of a general system of variational inclusion (1.11) with  -inverse strongly accretive mappings. To be more precise, they obtained the following results.
-inverse strongly accretive mappings. To be more precise, they obtained the following results.
Lemma 1.8 (see [16]).
For any  where
where  ,
,  is a solution of the problem (1.11) if and only if
is a solution of the problem (1.11) if and only if  is a fixed point of the mapping
is a fixed point of the mapping  defined by
defined by

Theorem QCCK (see [16, Theorem  ]).
]).
Let  be a uniformly convex and
be a uniformly convex and  -uniformly smooth Banach space with the smoothness constant
-uniformly smooth Banach space with the smoothness constant  . Let
. Let  be a maximal monotone mapping and
be a maximal monotone mapping and  a
a  -inverse-strongly accretive mapping, respectively, for each
-inverse-strongly accretive mapping, respectively, for each  . Let
. Let  be a
be a  -strict pseudocontraction such that
-strict pseudocontraction such that  . Define a mapping
. Define a mapping  by
by  ,
,  . Assume that
. Assume that  , where
, where  is defined as in Lemma 1.8. Let
is defined as in Lemma 1.8. Let  and let
and let  be a sequence generated by
be a sequence generated by

where  ,
,  ,
,  , and
, and  and
and  are sequences in
are sequences in  . If the control consequences
. If the control consequences  and
and  satisfy the following restrictions:
satisfy the following restrictions:
(C1) ,
,
(C2) and
and  ,
,
then  converges strongly to
converges strongly to  , where
, where  is the sunny nonexpansive retraction from
is the sunny nonexpansive retraction from  onto
onto  and
and  , where
, where  , is a solution to problem (1.11).
, is a solution to problem (1.11).
On the other hand, we recall the following well-known definitions and results.
In a smooth Banach space, a mapping  is called strongly positive [17] if there exists a constant
is called strongly positive [17] if there exists a constant  with property
with property

where  is the identity mapping and
is the identity mapping and  is the normalized duality mapping.
is the normalized duality mapping.
In [18], Moudafi introduced the viscosity approximation method for nonexpansive mappings (see [19] for further developments in both Hilbert and Banach spaces). Let  be a contraction on
be a contraction on  . Starting with an arbitrary initial point
. Starting with an arbitrary initial point  , define a sequence
, define a sequence  recursively by
recursively by

where  is a sequence in
is a sequence in  . It is proved [18, 19] that, under certain appropriate conditions imposed on
. It is proved [18, 19] that, under certain appropriate conditions imposed on  , the sequence
, the sequence  generated by (1.28) strongly converges to the unique solution
generated by (1.28) strongly converges to the unique solution  in
in  of the variational inequality
of the variational inequality

Recently, Marino and Xu [20] introduced the following general iterative method:

where  is a strongly positive bounded linear operator on a Hilbert space
is a strongly positive bounded linear operator on a Hilbert space  . They proved that, if the sequence
. They proved that, if the sequence  of parameters satisfies appropriate conditions, then the sequence
of parameters satisfies appropriate conditions, then the sequence  generated by (1.30) converges strongly to the unique solution of the variational inequality
generated by (1.30) converges strongly to the unique solution of the variational inequality

which is the optimality condition for the minimization problem

where  is a potential function for
is a potential function for  for
for  ).
).
Recently, Qin et al. [21] introduce the following iterative algorithm scheme:

where  is nonself-
is nonself- -strict pseudo-contraction,
-strict pseudo-contraction,  is a contraction, and
is a contraction, and  is a strongly positive bounded linear operator on a Hilbert space
is a strongly positive bounded linear operator on a Hilbert space  . They proved, under certain appropriate conditions imposed on the sequences
. They proved, under certain appropriate conditions imposed on the sequences  and
and  , that
, that  defined by (1.33) converges strongly to a fixed point of
defined by (1.33) converges strongly to a fixed point of  , which solves some variational inequality.
, which solves some variational inequality.
In this paper, motivated by Qin et al. [16], Moudafi [18], Marino and Xu [20], and Qin et al. [21], we introduce a general iterative approximation method for finding common elements of the set of solutions to a general system of variational inclusions (1.11) with Lipschitzian and relaxed cocoercive mappings and the set common fixed points of a countable family of strict pseudocontractions. We prove the strong convergence theorems of such iterative scheme for finding a common element of such two sets which is a unique solution of some variational inequality and is also the optimality condition for some minimization problems in strictly convex and  -uniformly smooth Banach spaces. The results presented in this paper improve and extend the corresponding results announced by Qin et al. [16], Moudafi [18], Marino and Xu [20], Qin et al. [21], and many others.
-uniformly smooth Banach spaces. The results presented in this paper improve and extend the corresponding results announced by Qin et al. [16], Moudafi [18], Marino and Xu [20], Qin et al. [21], and many others.
2. Preliminaries
Now we collect some useful lemmas for proving the convergence result of this paper.
Lemma 2.1 (see [22]).
The resolvent operator  associated with
associated with  is single valued and nonexpansive for all
is single valued and nonexpansive for all  .
.
Lemma 2.2 (see [13]).

is a solution of variational inclusion (1.13) if and only if 
 ; that is,
; that is,

where  denotes the set of solutions to problem (1.13).
denotes the set of solutions to problem (1.13).
Lemma 2.3 (see [23]).
Let  be a strictly convex Banach space. Let
be a strictly convex Banach space. Let  and
and  be two nonexpansive mappings from
be two nonexpansive mappings from  into itself with a common fixed point. Define a mapping
into itself with a common fixed point. Define a mapping  by
by

where  is a constant in
is a constant in  . Then
. Then  is nonexpansive and
is nonexpansive and  .
.
Lemma 2.4 (see [24]).
Let  be a nonempty closed convex subset of reflexive Banach space
be a nonempty closed convex subset of reflexive Banach space  which satisfies Opial's condition, and suppose that
which satisfies Opial's condition, and suppose that  is nonexpansive. Then the mapping
is nonexpansive. Then the mapping  is demiclosed at zero, that is,
is demiclosed at zero, that is,  imply that
imply that  .
.
Lemma 2.5 (see [25]).
Assume that  is a sequence of nonnegative real numbers such that
is a sequence of nonnegative real numbers such that

where  is a sequence in
is a sequence in  and
and  is a sequence such that
is a sequence such that
(a) ,
,
(b) or
or 
Then 
Lemma 2.6 (see [26]).
Let  and
and  be bounded sequences in a Banach space
be bounded sequences in a Banach space  and
and  a sequence in
a sequence in  with
with  . Suppose that
. Suppose that  for all
for all  and
and

Then 
Definition 2.7 (see [27]).
Let  be a family of mappings from a subset
be a family of mappings from a subset  of a Banach space
of a Banach space  into
into  with
with  . We say that
. We say that  satisfies the AKTT-condition if, for each bounded subset
satisfies the AKTT-condition if, for each bounded subset  of
of  ,
,

Remark 2.8.
The example of the sequence of mappings  satisfying AKTT-condition is supported by Example 3.11.
satisfying AKTT-condition is supported by Example 3.11.
Lemma 2.9 (see [27, Lemma  ]).
]).
Suppose that  satisfies AKTT-condition. Then, for each
satisfies AKTT-condition. Then, for each  ,
,  converses strongly to a point in
converses strongly to a point in  . Moreover, let the mapping
. Moreover, let the mapping  be defined by
be defined by

Then for each bounded subset  of
of  ,
, 
Lemma 2.10 (see [28]).
Let  be a real
be a real  -uniformly smooth Banach space and
-uniformly smooth Banach space and  a
a  -strict pseudocontraction. Then
-strict pseudocontraction. Then  is nonexpansive and
is nonexpansive and  .
.
Lemma 2.11 (see [29]).
Let  be a real
be a real  -uniformly smooth Banach space with the best smoothness constant
-uniformly smooth Banach space with the best smoothness constant  . Then the following inequality holds:
. Then the following inequality holds:

Lemma 2.12 (see [17, Lemma  ]).
]).
Assume that  is a strongly positive linear bounded operator on a smooth Banach space
is a strongly positive linear bounded operator on a smooth Banach space  with coefficient
with coefficient  and
and  Then
Then 
3. Main Results
In this section, we prove that the strong convergence theorem for a countable family of uniformly  -strict pseudocontractions in a strictly convex and
-strict pseudocontractions in a strictly convex and  -uniformly smooth Banach space admits a weakly sequentially continuous duality mapping. Before proving it, we need the following theorem.
-uniformly smooth Banach space admits a weakly sequentially continuous duality mapping. Before proving it, we need the following theorem.
Theorem 3.1 (see [17, Lemma  ]).
]).
Let  be a nonempty closed convex subset of a reflexive, smooth Banach space
be a nonempty closed convex subset of a reflexive, smooth Banach space  which admits a weakly sequentially continuous duality mapping
which admits a weakly sequentially continuous duality mapping  from
from  to
to  . Let
. Let  be a nonexpansive mapping such that
be a nonexpansive mapping such that  is nonempty, let
is nonempty, let  be a contraction with coefficient
be a contraction with coefficient  , and let
, and let  be a strongly positive bounded linear operator with coefficient
be a strongly positive bounded linear operator with coefficient  and
and  . Then the net
. Then the net  defined by
defined by

converges strongly as  to a fixed point
to a fixed point  of
of  which solves the variational inequality:
which solves the variational inequality:

Lemma 3.2.
Let  be a nonempty closed convex subset of a real
be a nonempty closed convex subset of a real  -uniformly smooth Banach space
-uniformly smooth Banach space  with the smoothness constant
with the smoothness constant  . Let
. Let  be an
be an  -Lipschitzian and relaxed
-Lipschitzian and relaxed  -cocoercive mapping. Then
-cocoercive mapping. Then

If  , then
, then  is nonexpansive.
is nonexpansive.
Proof.
Using Lemma 2.11 and the cocoercivity of the mapping  , we have, for all
, we have, for all  ,
,

Hence (3.3) is proved. Assume that  . Then, we have
. Then, we have  . This together with (3.3) implies that
. This together with (3.3) implies that  is nonexpansive.
is nonexpansive.
Lemma 3.3.
Let  be a strictly convex and
be a strictly convex and  -uniformly smooth Banach space admiting a weakly sequentially continuous duality mapping with the smoothness constant
-uniformly smooth Banach space admiting a weakly sequentially continuous duality mapping with the smoothness constant  . Let
. Let  be a maximal monotone mapping and
be a maximal monotone mapping and  a
a  -Lipschitzian and relaxed
-Lipschitzian and relaxed  -cocoercive mapping with
-cocoercive mapping with  , respectively, for each
, respectively, for each  . Let
. Let  be a countable family of uniformly
be a countable family of uniformly  -strict pseudocontractions. Define a mapping
-strict pseudocontractions. Define a mapping  and
and  by
by

where  is defined as in Lemma 1.8. Assume that
is defined as in Lemma 1.8. Assume that  . Let
. Let  be an
be an  -contraction; let
-contraction; let  be a strongly positive linear bounded self-adjoint operator with coefficient
be a strongly positive linear bounded self-adjoint operator with coefficient  with
with  . Then the following hold.
. Then the following hold.
(i)For each  ,
,  is nonexpansive such that
is nonexpansive such that

(ii)Suppose that  satisfies AKTT-condition. Let
satisfies AKTT-condition. Let  be the mapping defined by
be the mapping defined by  for all
for all  and suppose that
and suppose that  . The net
. The net  defined by
defined by  converges strongly as
converges strongly as  to a fixed point
to a fixed point  of
of  , which solves the variational inequality
, which solves the variational inequality

and  is a solution of general system of variational inequality problem (1.11) such that
is a solution of general system of variational inequality problem (1.11) such that  .
.
Proof.
It follows from Lemma 2.10 that  is nonexpansive such that
is nonexpansive such that  for each
for each  . Next, we prove that
. Next, we prove that  is nonexpansive. Indeed, we observe that
is nonexpansive. Indeed, we observe that

The nonexpansivity of  ,
,  ,
,  , and
, and  implies that
implies that  is nonexpansive. By Lemma 2.3, we have that
is nonexpansive. By Lemma 2.3, we have that  is nonexpansive such that
is nonexpansive such that

Hence (i) is proved. It is well known that, if  is uniformly smooth, then
is uniformly smooth, then  is reflexive. Hence Theorem 3.1 implies that
is reflexive. Hence Theorem 3.1 implies that  converges strongly as
converges strongly as  to a fixed point
to a fixed point  of
of  , which solves the variational inequality
, which solves the variational inequality

and  is a solution of problem (1.11), where
is a solution of problem (1.11), where  . This completes the proof of (ii).
. This completes the proof of (ii).
Theorem 3.4.
Let  be a strictly convex and
be a strictly convex and  -uniformly smooth Banach space which admits a weakly sequentially continuous duality mapping and has the smoothness constant
-uniformly smooth Banach space which admits a weakly sequentially continuous duality mapping and has the smoothness constant  . Let
. Let  be a maximal monotone mapping and
be a maximal monotone mapping and  a
a  -Lipschitzian and relaxed
-Lipschitzian and relaxed  -cocoercive mapping with
-cocoercive mapping with  , respectively, for each
, respectively, for each  . Let
. Let  be a countable family of uniformly
be a countable family of uniformly  -strict pseudocontractions. Define a mapping
-strict pseudocontractions. Define a mapping  by
by

Assume that  , where
, where  is defined as in Lemma 1.8. Let
is defined as in Lemma 1.8. Let  be an
be an  -contraction; let
-contraction; let  be a strongly positive linear bounded self adjoint operator with coefficient
be a strongly positive linear bounded self adjoint operator with coefficient  with
with  . Let
. Let  and let
and let  be a sequence generated by
be a sequence generated by

where  , and
, and  and
and  are sequences in
are sequences in  . Suppose that
. Suppose that  satisfies AKTT-condition. Let
satisfies AKTT-condition. Let  be the mapping defined by
be the mapping defined by  for all
for all  and suppose that
and suppose that  . If the control consequences
. If the control consequences  and
and  satisfy the following restrictions
satisfy the following restrictions
(C1) ,
,
(C2) and
and  ,
,
then  converges strongly to
converges strongly to  , which solves the variational inequality
, which solves the variational inequality

and  is a solution of general system of variational inequality problem (1.11) such that
is a solution of general system of variational inequality problem (1.11) such that  .
.
Proof.
First, we show that sequences  ,
,  , and
, and  are bounded.
are bounded.
By the control condition (C2), we may assume, with no loss of generality, that  .
.
Since  is a linear bounded operator on
is a linear bounded operator on  , by (1.27), we have
, by (1.27), we have

Observe that

It follows that

Therefore, taking  one has
one has

Putting  one sees that
one sees that

It follows from Lemmas 2.1 and 3.2 that

This implies that

Setting  and applying Lemma 2.10, we have that
and applying Lemma 2.10, we have that  is a nonexpansive mapping such that
is a nonexpansive mapping such that  for all
for all  and hence
and hence  . Then
. Then

It follows from the last inequality that

By induction, we have

This shows that the sequence  is bounded, and so are
is bounded, and so are  ,
,  , and
, and  .
.
On the other hand, from the nonexpansivity of the mappings  , one sees that
, one sees that

In a similar way, one can obtain that

It follows that

This implies that

Setting

one sees that

and so it follows that

which, combined, with (3.27) yields that

Using the conditions (C1) and (C2) and AKTT-condition of  , we have
, we have

Hence, from Lemma 2.6, it follows that

From (3.28), it follows that

By (3.33), one sees that

On the other hand, one has

It follows that

From the conditions (C1), (C2) and from (3.35), one sees that

Define the mapping  by
by

where  is defined as in Lemma 1.8. From Lemma 3.3(i), we see that
is defined as in Lemma 1.8. From Lemma 3.3(i), we see that  is nonexpansive such that
is nonexpansive such that

From (3.38), it follows that

Since  satisfies AKTT-condition and
satisfies AKTT-condition and  is the mapping defined by
is the mapping defined by  for all
for all  , we have that
, we have that  satisfies AKTT-condition. Let the mapping
satisfies AKTT-condition. Let the mapping  be the mapping defined by
be the mapping defined by  for all
for all  . It follows from the nonexpansivity of
. It follows from the nonexpansivity of  and
and

that  is nonexpansive such that
is nonexpansive such that

Next, we prove that

where  with
with  be the fixed point of the contraction
be the fixed point of the contraction

Then  solves the fixed point equation
solves the fixed point equation  . It follows from Lemma 3.3(ii) that
. It follows from Lemma 3.3(ii) that  , which solves the variational inequality:
, which solves the variational inequality:

and  is a solution of general system of variational inequality problem (1.11) such that
is a solution of general system of variational inequality problem (1.11) such that  . Let
. Let  be a subsequence of
be a subsequence of  such that
such that

If follows from reflexivity of  and the boundedness of sequence
and the boundedness of sequence  that there exists
that there exists  which is a subsequence of
which is a subsequence of  converging weakly to
converging weakly to  as
as  . It follows from (3.41) and the nonexpansivity of
. It follows from (3.41) and the nonexpansivity of  , we have
, we have  by Lemma 2.4. Since the duality map
by Lemma 2.4. Since the duality map  is single valued and weakly sequentially continuous from
is single valued and weakly sequentially continuous from  to
to  , we get that
, we get that

as required. Now from Lemma 2.11, we have

which implies that

where  is an appropriate constant such that
is an appropriate constant such that  . Put
. Put

that is,

It follows from conditions (C1), (C2) and from (3.44) that

Apply Lemma 2.5 to (3.52) to conclude that  as
as  . This completes the proof.
. This completes the proof.
Setting  , and
, and  , we have the following result.
, we have the following result.
Theorem 3.5.
Let  be a strictly convex and
be a strictly convex and  -uniformly smooth Banach space which admits a weakly sequentially continuous duality mapping and has the smoothness constant
-uniformly smooth Banach space which admits a weakly sequentially continuous duality mapping and has the smoothness constant  . Let
. Let  be a maximal monotone mapping and
be a maximal monotone mapping and  a
a  -Lipschitzian and relaxed
-Lipschitzian and relaxed  -cocoercive mapping with
-cocoercive mapping with  , respectively, for each
, respectively, for each  . Let
. Let  be a countable family of uniformly
be a countable family of uniformly  -strict pseudocontractions. Define a mapping
-strict pseudocontractions. Define a mapping  by
by

Assume that  , where
, where  is defined as in Lemma 1.8. Let
is defined as in Lemma 1.8. Let  and let
and let  be a sequence generated by
be a sequence generated by

where  , and
, and  and
and  are sequences in
are sequences in  . Suppose that
. Suppose that  satisfies AKTT-condition. Let
satisfies AKTT-condition. Let  be the mapping defined by
be the mapping defined by  for all
for all  and suppose that
and suppose that  . If the control consequences
. If the control consequences  and
and  satisfy the following restrictions
satisfy the following restrictions
(C1) ,
,
(C2) and
and  ,
,
then  converges strongly to
converges strongly to  , which solves the variational inequality
, which solves the variational inequality

and  is a solution of general system of variational inequality problem (1.11) such that
is a solution of general system of variational inequality problem (1.11) such that  .
.
Remark 3.6.
Theorem 3.4 mainly improves Theorem  of Qin et al. [16], in the following respects:
of Qin et al. [16], in the following respects:
(a)from the class of inverse-strongly accretive mappings to the class of Lipchitzian and relaxed cocoercive mappings,
(b)from a  -strict pseudocontraction to the countable family of uniformly
-strict pseudocontraction to the countable family of uniformly  -strict pseudocontractions,
-strict pseudocontractions,
(c)from a uniformly convex and  -uniformly smooth Banach space to a strictly convex and
-uniformly smooth Banach space to a strictly convex and  -uniformly smooth Banach space which admits a weakly sequentially continuous duality mapping.
-uniformly smooth Banach space which admits a weakly sequentially continuous duality mapping.
Further, if  is a countable family of nonexpansive mappings, then Theorem 3.4 is reduced to the following result.
is a countable family of nonexpansive mappings, then Theorem 3.4 is reduced to the following result.
Theorem 3.7.
Let  be a strictly convex and
be a strictly convex and  -uniformly smooth Banach space which admits a weakly sequentially continuous duality mapping and has the smoothness constant
-uniformly smooth Banach space which admits a weakly sequentially continuous duality mapping and has the smoothness constant  . Let
. Let  be a maximal monotone mapping and
be a maximal monotone mapping and  a
a  -Lipschitzian and relaxed
-Lipschitzian and relaxed  -cocoercive mapping with
-cocoercive mapping with  , respectively, for each
, respectively, for each  . Let
. Let  be a countable family of nonexpansive mappings. Assume that
be a countable family of nonexpansive mappings. Assume that  , where
, where  is defined as in Lemma 1.8. Let
is defined as in Lemma 1.8. Let  be an
be an  -contraction; let
-contraction; let  be a strongly positive linear bounded self adjoint operator with coefficient
be a strongly positive linear bounded self adjoint operator with coefficient  with
with  . Let
. Let  and let
and let  be a sequence generated by
be a sequence generated by

where  , and
, and  and
and  are sequences in
are sequences in  . Suppose that
. Suppose that  satisfies AKTT-condition. Let
satisfies AKTT-condition. Let  be the mapping defined by
be the mapping defined by  for all
for all  and suppose that
and suppose that  . If the control consequences
. If the control consequences  and
and  satisfy the following restrictions
satisfy the following restrictions
(C1) ,
,
(C2) and
and  ,
,
then  converges strongly to
converges strongly to  which solves the variational inequality:
which solves the variational inequality:

and  is a solution of general system of variational inequality problem (1.11) such that
is a solution of general system of variational inequality problem (1.11) such that  .
.
Remark 3.8.
As in [27, Theorem  ], we can generate a sequence
], we can generate a sequence  of nonexpansive mappings satisfying AKTT-condition; that is,
of nonexpansive mappings satisfying AKTT-condition; that is,  for any bounded subset
for any bounded subset  of
of  by using convex combination of a general sequence
by using convex combination of a general sequence  of nonexpansive mappings with a common fixed point. To be more precise, they obtained the following lemma.
of nonexpansive mappings with a common fixed point. To be more precise, they obtained the following lemma.
Lemma 3.9 (see [27]).
Let  be a closed convex subset of a smooth Banach space
be a closed convex subset of a smooth Banach space  . Suppose that
. Suppose that  is a sequence of nonexpansive mappings of
is a sequence of nonexpansive mappings of  into inself with a common fixed point. For each
into inself with a common fixed point. For each  , define
, define  by
by

where  is a family of nonnegative numbers with indices
is a family of nonnegative numbers with indices  with
with  such that
such that
(i) for all
for all  ,
,
(ii) for every
for every  ,
,
(iii) .
.
Then the following are given.
()Each  is a nonexpansive mapping.
is a nonexpansive mapping.
() satisfies AKTT-condition.
satisfies AKTT-condition.
()If  is defined by
is defined by

then  and
and  .
.
Theorem 3.10.
Let  be a strictly convex and
be a strictly convex and  -uniformly smooth Banach space which admits a weakly sequentially continuous duality mapping and has the smoothness constant
-uniformly smooth Banach space which admits a weakly sequentially continuous duality mapping and has the smoothness constant  . Let
. Let  be a maximal monotone mapping and
be a maximal monotone mapping and  a
a  -Lipschitzian and relaxed
-Lipschitzian and relaxed  -cocoercive mapping with
-cocoercive mapping with  , respectively, for each
, respectively, for each  . Let
. Let  be a countable family of nonexpansive mappings. Assume that
be a countable family of nonexpansive mappings. Assume that  , where
, where  is defined as in Lemma 1.8. Let
is defined as in Lemma 1.8. Let  be an
be an  -contraction; let
-contraction; let  be a strongly positive linear bounded self adjoint operator with coefficient
be a strongly positive linear bounded self adjoint operator with coefficient  with
with  . Let
. Let  and let
and let  be a sequence generated by
be a sequence generated by

where  satisfies conditions (i)–(iii) of Lemma 3.9,
satisfies conditions (i)–(iii) of Lemma 3.9,  , and
, and  and
and  are sequences in
are sequences in  . Suppose that
. Suppose that  satisfies AKTT-condition. Let
satisfies AKTT-condition. Let  be the mapping defined by
be the mapping defined by  for all
for all  and suppose that
and suppose that  . If the control consequences
. If the control consequences  and
and  satisfy the following restrictions:
satisfy the following restrictions:
(C1) ,
,
(C2) and
and  ,
,
then  converges strongly to
converges strongly to  , which solves the variational inequality
, which solves the variational inequality

and  is a solution of general system of variational inequality problem (1.11) such that
is a solution of general system of variational inequality problem (1.11) such that  .
.
Proof.
We write the iteration (3.61) as

where  is defined by (3.59). It is clear that each mapping
is defined by (3.59). It is clear that each mapping  is nonexpansive. By Theorem 3.7 and Lemma 3.9, the conclusion follows.
is nonexpansive. By Theorem 3.7 and Lemma 3.9, the conclusion follows.
The following example appears in [27] shows that there exists  satisfying the conditions of Lemma 3.9.
satisfying the conditions of Lemma 3.9.
Example 3.11.
Let
 be defined by
be defined by

for all  with
with  In this case, the sequence
In this case, the sequence  of mappings generated by
of mappings generated by  is defined as follows: For
is defined as follows: For  .
.

References
Ball K, Carlen EA, Lieb EH: Sharp uniform convexity and smoothness inequalities for trace norms. Inventiones Mathematicae 1994, 115(3):463–482.
Gossez J-P, Lami Dozo E: Some geometric properties related to the fixed point theory for nonexpansive mappings. Pacific Journal of Mathematics 1972, 40: 565–573.
Browder FE, Petryshyn WV: Construction of fixed points of nonlinear mappings in Hilbert space. Journal of Mathematical Analysis and Applications 1967, 20: 197–228. 10.1016/0022-247X(67)90085-6
Verma RU: Approximation-solvability of a class of A-monotone variational inclusion problems. Journal of the Korean Society for Industrial and Applied Mathematics 2004, 8(1):55–66.
Verma RU: General over-relaxed proximal point algorithm involving
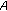 -maximal relaxed monotone mappings with applications. Nonlinear Analysis: Theory, Methods & Applications 2009, 71(12):e1461-e1472. 10.1016/j.na.2009.01.184
-maximal relaxed monotone mappings with applications. Nonlinear Analysis: Theory, Methods & Applications 2009, 71(12):e1461-e1472. 10.1016/j.na.2009.01.184R. U. Verma, A-monotonicity and applications to nonlinear variational inclusion problems, Journalof Applied Mathematics and Stochastic Analysis, no. 2, pp. 193–195, 2004.
Aoyama K, Iiduka H, Takahashi W: Weak convergence of an iterative sequence for accretive operators in Banach spaces. Fixed Point Theory and Applications 2006, 2006:-13.
Reich S: Asymptotic behavior of contractions in Banach spaces. Journal of Mathematical Analysis and Applications 1973, 44: 57–70. 10.1016/0022-247X(73)90024-3
Kitahara S, Takahashi W: Image recovery by convex combinations of sunny nonexpansive retractions. Topological Methods in Nonlinear Analysis 1993, 2(2):333–342.
Browder FE: Fixed-point theorems for noncompact mappings in Hilbert space. Proceedings of the National Academy of Sciences of the United States of America 1965, 53: 1272–1276. 10.1073/pnas.53.6.1272
Reich S: Strong convergence theorems for resolvents of accretive operators in Banach spaces. Journal of Mathematical Analysis and Applications 1980, 75(1):287–292. 10.1016/0022-247X(80)90323-6
Ceng L-C, Wang C-Y, Yao J-C: Strong convergence theorems by a relaxed extragradient method for a general system of variational inequalities. Mathematical Methods of Operations Research 2008, 67(3):375–390. 10.1007/s00186-007-0207-4
Zhang S-S, Lee JHW, Chan CK: Algorithms of common solutions to quasi variational inclusion and fixed point problems. Applied Mathematics and Mechanics 2008, 29(5):571–581. 10.1007/s10483-008-0502-y
Cho YJ, Yao Y, Zhou H: Strong convergence of an iterative algorithm for accretive operators in Banach spaces. Journal of Computational Analysis and Applications 2008, 10(1):113–125.
Hao Y: Strong convergence of an iterative method for inverse strongly accretive operators. Journal of Inequalities and Applications 2008, 2008:-9.
Qin X, Chang SS, Cho YJ, Kang SM: Approximation of solutions to a system of variational inclusions in Banach spaces. Journal of Inequalities and Applications 2010, 2010:-16.
Cai G, Hu CS: Strong convergence theorems of a general iterative process for a finite family of
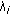 -strict pseudo-contractions in -uniformly smooth Banach spaces. Computers & Mathematics with Applications 2010, 59(1):149–160. 10.1016/j.camwa.2009.07.068
-strict pseudo-contractions in -uniformly smooth Banach spaces. Computers & Mathematics with Applications 2010, 59(1):149–160. 10.1016/j.camwa.2009.07.068Moudafi A: Viscosity approximation methods for fixed-points problems. Journal of Mathematical Analysis and Applications 2000, 241(1):46–55. 10.1006/jmaa.1999.6615
Xu H-K: Viscosity approximation methods for nonexpansive mappings. Journal of Mathematical Analysis and Applications 2004, 298(1):279–291. 10.1016/j.jmaa.2004.04.059
Marino G, Xu H-K: A general iterative method for nonexpansive mappings in Hilbert spaces. Journal of Mathematical Analysis and Applications 2006, 318(1):43–52. 10.1016/j.jmaa.2005.05.028
Qin X, Shang M, Kang SM: Strong convergence theorems of modified Mann iterative process for strict pseudo-contractions in Hilbert spaces. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(3):1257–1264. 10.1016/j.na.2008.02.009
Aoyama K, Kimura Y, Takahashi W, Toyoda M: On a strongly nonexpansive sequence in Hilbert spaces. Journal of Nonlinear and Convex Analysis 2007, 8(3):471–489.
Bruck RE Jr.: Properties of fixed-point sets of nonexpansive mappings in Banach spaces. Transactions of the American Mathematical Society 1973, 179: 251–262.
Jung JS: Iterative approaches to common fixed points of nonexpansive mappings in Banach spaces. Journal of Mathematical Analysis and Applications 2005, 302(2):509–520. 10.1016/j.jmaa.2004.08.022
Xu H-K: Iterative algorithms for nonlinear operators. Journal of the London Mathematical Society 2002, 66(1):240–256. 10.1112/S0024610702003332
Suzuki T: Strong convergence of Krasnoselskii and Mann's type sequences for one-parameter nonexpansive semigroups without Bochner integrals. Journal of Mathematical Analysis and Applications 2005, 305(1):227–239. 10.1016/j.jmaa.2004.11.017
Aoyama K, Kimura Y, Takahashi W, Toyoda M: Approximation of common fixed points of a countable family of nonexpansive mappings in a Banach space. Nonlinear Analysis: Theory, Methods & Applications 2007, 67(8):2350–2360. 10.1016/j.na.2006.08.032
Zhou H: Convergence theorems for
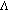 -strict pseudo-contractions in 2-uniformly smooth Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(9):3160–3173. 10.1016/j.na.2007.09.009
-strict pseudo-contractions in 2-uniformly smooth Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(9):3160–3173. 10.1016/j.na.2007.09.009Xu HK: Inequalities in Banach spaces with applications. Nonlinear Analysis: Theory, Methods & Applications 1991, 16(12):1127–1138. 10.1016/0362-546X(91)90200-K
Acknowledgments
The first author is supported under grant from the program Strategic Scholarships for Frontier Research Network for the Ph.D. Program Thai Doctoral degree from the Office of the Higher Education Commission, Thailand and the second author is supported by the "Centre of Excellence in Mathematics" under the Commission on Higher Education, Ministry of Education, Thailand. Finally, The authors would like to thank the referees for reading this paper carefully, providing valuable suggestions and comments, and pointing out a major error in the original version of this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kamraksa, U., Wangkeeree, R. A General Iterative Process for Solving a System of Variational Inclusions in Banach Spaces. J Inequal Appl 2010, 190126 (2010). https://doi.org/10.1155/2010/190126
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/190126
 -maximal relaxed monotone mappings with applications. Nonlinear Analysis: Theory, Methods & Applications 2009, 71(12):e1461-e1472. 10.1016/j.na.2009.01.184
-maximal relaxed monotone mappings with applications. Nonlinear Analysis: Theory, Methods & Applications 2009, 71(12):e1461-e1472. 10.1016/j.na.2009.01.184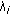 -strict pseudo-contractions in -uniformly smooth Banach spaces. Computers & Mathematics with Applications 2010, 59(1):149–160. 10.1016/j.camwa.2009.07.068
-strict pseudo-contractions in -uniformly smooth Banach spaces. Computers & Mathematics with Applications 2010, 59(1):149–160. 10.1016/j.camwa.2009.07.068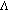 -strict pseudo-contractions in 2-uniformly smooth Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(9):3160–3173. 10.1016/j.na.2007.09.009
-strict pseudo-contractions in 2-uniformly smooth Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(9):3160–3173. 10.1016/j.na.2007.09.009