- Research Article
- Open access
- Published:
Stability of Approximate Quadratic Mappings
Journal of Inequalities and Applications volume 2010, Article number: 184542 (2010)
Abstract
We investigate the general solution of the quadratic functional equation  , in the class of all functions between quasi-
, in the class of all functions between quasi- -normed spaces, and then we prove the generalized Hyers-Ulam stability of the equation by using direct method and fixed point method.
-normed spaces, and then we prove the generalized Hyers-Ulam stability of the equation by using direct method and fixed point method.
1. Introduction
In 1940, Ulam [1] gave a talk before the Mathematics Club of the University of Wisconsin in which he discussed a number of unsolved problems. Among these was the following question concerning the stability of homomorphisms.
Let
 be a group and let
be a group and let
 be a metric group with metric
be a metric group with metric
 . Given
. Given
 , does there exist a
, does there exist a
 such that if
such that if
 satisfies
satisfies
 for all
for all
 , then a homomorphism
, then a homomorphism
 exists with
exists with
 for all
for all
 ?
?
In 1941, the first result concerning the stability of functional equations was presented by Hyers [2]. And then Aoki [3] and Bourgin [4] have investigated the stability theorems of functional equations with unbounded Cauchy differences. In 1978, Th. M. Rassias [5] provided a generalization of Hyers' Theorem which allows the Cauchy difference to be unbounded. It was shown by Gajda [6] as well as by Th. M. Rassias and Šemrl [7] that one cannot prove the Rassias' type theorem when  . Găvruta [8] obtained generalized result of Th. M. Rassias' Theorem which allow the Cauchy difference to be controlled by a general unbounded function. J. M. Rassias [9, 10] established a similar stability theorem linear and nonlinear mappings with the unbounded Cauchy difference.
. Găvruta [8] obtained generalized result of Th. M. Rassias' Theorem which allow the Cauchy difference to be controlled by a general unbounded function. J. M. Rassias [9, 10] established a similar stability theorem linear and nonlinear mappings with the unbounded Cauchy difference.
Let  and
and  be real vector spaces. A function
be real vector spaces. A function  is called a quadratic function if and only if
is called a quadratic function if and only if  is a solution function of the quadratic functional equation:
is a solution function of the quadratic functional equation:

It is well known that a function  between real vector spaces is quadratic if and only if there exists a unique symmetric biadditive function
between real vector spaces is quadratic if and only if there exists a unique symmetric biadditive function  such that
such that  for all
for all  , where the mapping
, where the mapping  is given by
is given by  . See [11, 12] for the details. The Hyers-Ulam stability of the quadratic functional (1.1) was first proved by Skof [13] for functions
. See [11, 12] for the details. The Hyers-Ulam stability of the quadratic functional (1.1) was first proved by Skof [13] for functions  , where
, where  is a normed space and
is a normed space and  is a Banach space. Cholewa [14] demonstrated that Skof's theorem is also valid if
is a Banach space. Cholewa [14] demonstrated that Skof's theorem is also valid if  is replaced by an abelian group. Czerwik [15] proved the Hyers-Ulam stability of quadratic functional (1.1) by the similar way to Th. M. Rassias control function [5]. According to the theorem of Borelli and Forti [16], we obtain the following generalization of stability theorem for the quadratic functional (1.1): let
is replaced by an abelian group. Czerwik [15] proved the Hyers-Ulam stability of quadratic functional (1.1) by the similar way to Th. M. Rassias control function [5]. According to the theorem of Borelli and Forti [16], we obtain the following generalization of stability theorem for the quadratic functional (1.1): let  be an abelian group and
be an abelian group and  a Banach space; let
a Banach space; let  be a mapping with
be a mapping with  satisfying the inequality
satisfying the inequality

for all  . Assume that one of the following conditions
. Assume that one of the following conditions

holds for all  , then there exists a unique quadratic function
, then there exists a unique quadratic function  such that
such that

for all  . The stability problems of several functional equations have been extensively investigated by a number of authors and there are many interesting results concerning this problem [17–23].
. The stability problems of several functional equations have been extensively investigated by a number of authors and there are many interesting results concerning this problem [17–23].
In this paper, we consider a new quadratic functional equation

for all vectors in quasi- -normed spaces. First, we note that a function
-normed spaces. First, we note that a function  is a solution of the functional (1.5) in the class of all functions between vector spaces if and only if the function
is a solution of the functional (1.5) in the class of all functions between vector spaces if and only if the function  is quadratic. Further, we investigate the generalized Hyers-Ulam stability of (1.5) by using direct method and fixed point method. As a result of the paper, we have a much better possible estimation of approximate quadratic mappings by quadratic mappings than that of Czerwik [15] and Skof [13].
is quadratic. Further, we investigate the generalized Hyers-Ulam stability of (1.5) by using direct method and fixed point method. As a result of the paper, we have a much better possible estimation of approximate quadratic mappings by quadratic mappings than that of Czerwik [15] and Skof [13].
2. Stability of (1.5)
Now, we consider some basic concepts concerning quasi- -normed spaces and some preliminary results. We fix a real number
-normed spaces and some preliminary results. We fix a real number  with
with  and let
and let  denote either
denote either  or
or  . Let
. Let  be a linear space over
be a linear space over  . A quasi-
. A quasi- -norm
-norm is a real-valued function on
is a real-valued function on  satisfying the following.
satisfying the following.
(1) for all
for all  and
and  if and only if
if and only if  .
.
(2) for all
for all  and all
and all  .
.
(3) There is a constant  such that
such that  for all
for all  .
.
The pair  is called a
is called a  space if
space if  is a quasi-
is a quasi- -norm on
-norm on  . The smallest possible
. The smallest possible  is called the modulus of concavity of
is called the modulus of concavity of  . A
. A  space is a complete quasi-
space is a complete quasi- -normed space. A quasi-
-normed space. A quasi- -norm
-norm  is called a
is called a  -norm
-norm if
if

for all  . In this case, a quasi-
. In this case, a quasi- -Banach space is called a
-Banach space is called a  -Banach space. We can refer to [24, 25] for the concept of quasinormed spaces and
-Banach space. We can refer to [24, 25] for the concept of quasinormed spaces and  -Banach spaces. Given a
-Banach spaces. Given a  -norm, the formula
-norm, the formula  gives us a translation invariant metric on
gives us a translation invariant metric on  . By the Aoki-Rolewicz theorem [25] (see also [24]), each quasinorm is equivalent to some
. By the Aoki-Rolewicz theorem [25] (see also [24]), each quasinorm is equivalent to some  -norm. In [26], Tabor has investigated a version of the D. H. Hyers, Th. M. Rassias, and Z. Gajda theorem (see [5, 6]) in quasibanach spaces. Recently, J. M. Rassias and Kim [27] have obtained stability results of general additive equations in quasi-
-norm. In [26], Tabor has investigated a version of the D. H. Hyers, Th. M. Rassias, and Z. Gajda theorem (see [5, 6]) in quasibanach spaces. Recently, J. M. Rassias and Kim [27] have obtained stability results of general additive equations in quasi- -normed spaces.
-normed spaces.
From now on, let  be a quasi-
be a quasi- -normed space with norm
-normed space with norm  and let
and let  be a
be a  -Banach space with norm
-Banach space with norm  unless we give any specific reference. Now, we are ready to investigate the generalized Hyers-Ulam stability problem for the functional (1.5) using direct method.
unless we give any specific reference. Now, we are ready to investigate the generalized Hyers-Ulam stability problem for the functional (1.5) using direct method.
Theorem 2.1.
Assume that a function  satisfies
satisfies

for all  and that
and that  satisfies the following control conditions
satisfies the following control conditions

for all  . Then there exists a unique quadratic function
. Then there exists a unique quadratic function  satisfying
satisfying

for all  , where
, where  . The function
. The function  is defined as
is defined as

for all 
Proof.
Putting  in (2.2), we get
in (2.2), we get  . Replacing
. Replacing  by
by  in (2.2), we obtain
in (2.2), we obtain

for all  . Dividing (2.6) by
. Dividing (2.6) by  , we get
, we get

for all  where
where  . Now letting
. Now letting  and dividing
and dividing  in (2.7), we have
in (2.7), we have

for all  . Therefore we prove from the inequality (2.8) that for any integers
. Therefore we prove from the inequality (2.8) that for any integers  with
with 

Since the right-hand side of (2.9) tends to zero as  , the sequence
, the sequence  is Cauchy for all
is Cauchy for all  and thus converges by the completeness of
and thus converges by the completeness of  . Define
. Define  by
by

Letting  in (2.2), respectively, and dividing both sides by
in (2.2), respectively, and dividing both sides by  and after then taking the limit in the resulting inequality, we have
and after then taking the limit in the resulting inequality, we have

and so the function  is quadratic.
is quadratic.
Taking the limit in (2.9) with  as
as  , we obtain that
, we obtain that

which yields the estimation (2.4).
To prove the uniqueness of the quadratic function  subject to (2.4), let us assume that there exists a quadratic function
subject to (2.4), let us assume that there exists a quadratic function  which satisfies (1.5) and the inequality (2.4). Obviously, we obtain that
which satisfies (1.5) and the inequality (2.4). Obviously, we obtain that

for all  . Hence it follows from (2.4) that
. Hence it follows from (2.4) that

for all  . Therefore letting
. Therefore letting  , one has
, one has  for all
for all  , completing the proof of uniqueness.
, completing the proof of uniqueness.
Theorem 2.2.
Assume that a function  satisfies
satisfies

for all  and that
and that  satisfies conditions
satisfies conditions

for all  . Then there exists a unique quadratic function
. Then there exists a unique quadratic function  satisfying
satisfying

for all  . The function
. The function  is given by
is given by

for all 
Proof.
In this case,  since
since  and so
and so  by assumption.
by assumption.
Replacing  by
by  in (2.6), we obtain
in (2.6), we obtain

for  . Therefore we prove from inequality (2.19) that for any integers
. Therefore we prove from inequality (2.19) that for any integers  with
with 

for all  . Since the right-hand side of (2.20) tends to zero as
. Since the right-hand side of (2.20) tends to zero as  , the sequence
, the sequence  is Cauchy for all
is Cauchy for all  and thus converges by the completeness of
and thus converges by the completeness of  . Define
. Define  by
by

for all  .
.
Thereafter, applying the same argument as in the proof of Theorem 2.1, we obtain the desired result.
We now introduce a fundamental result of fixed point theory. We refer to [28] for the proof of it, and the reader is referred to papers [29–31].
Theorem 2.3.
Let  be a generalized complete metric space (i.e.,
be a generalized complete metric space (i.e.,  may assume infinite values). Assume that
may assume infinite values). Assume that  is a strictly contractive operator with the Lipschitz constant
is a strictly contractive operator with the Lipschitz constant  Then for a given element
Then for a given element  one of the following assertions is true:
one of the following assertions is true:
(A1) for all
for all  ;
;
(A2) there exists a nonnegative integer  such that
such that
(A2.1) for all
for all  ;
;
(A2.2) the sequence  converges to a fixed point
converges to a fixed point  of
of  ;
;
(A2.3)  is the unique fixed point of
is the unique fixed point of  in the set
in the set 
(A2.4)  for all
for all 
For an extensive theory of fixed point theorems and other nonlinear methods, the reader is referred to the book of Hyers et al. [32]. In 1996, Isac and Th. M. Rassias [33] applied the stability theory of functional equations to prove fixed point theorems and study some new applications in nonlinear analysis. Cădariu and Radu [29, 31] and Radu [34] applied the fixed point theorem of alternative to the investigation of Cauchy and Jensen functional equations. Recently, Jung et al. [35–40] and Jung and Rassias [41] have obtained the generalized Hyers-Ulam stability of functional equations via the fixed point method.
Now we are ready to investigate the generalized Hyers-Ulam stability problem for the functional (1.5) using the fixed point method.
Theorem 2.4.
Let  be a function with
be a function with  for which there exists a function
for which there exists a function  such that there exists a constant
such that there exists a constant  satisfying the inequalities
satisfying the inequalities


for all  . Then there exists a unique quadratic function
. Then there exists a unique quadratic function  defined by
defined by  such that
such that

for all 
Proof.
Let us define  to be the set of all functions
to be the set of all functions  and introduce a generalized metric
and introduce a generalized metric  on
on  as follows:
as follows:

Then it is easy to show that  is complete (see [37, Proof of Theorem
is complete (see [37, Proof of Theorem  ]). Now we define an operator
]). Now we define an operator  by
by

for all  First, we assert that
First, we assert that  is strictly contractive with constant
is strictly contractive with constant  on
on  . Given
. Given  , let
, let  be an arbitrary constant with
be an arbitrary constant with  that is,
that is,  Then it follows from (2.23) that
Then it follows from (2.23) that

for all  that is,
that is,  for any
for any  with
with  Thus we see that
Thus we see that  for any
for any  and so
and so  is strictly contractive with constant
is strictly contractive with constant  on
on  .
.
Next, if we put  in (2.22) and we divide both sides by
in (2.22) and we divide both sides by  , then we get
, then we get

for all  which implies
which implies 
Thus applying Theorem 2.3 to the complete generalized metric space  with contractive constant
with contractive constant  , we see from
, we see from  of Theorem 2.3 that there exists a function
of Theorem 2.3 that there exists a function  which is a fixed point of
which is a fixed point of  , that is,
, that is,  such that
such that  as
as  By mathematical induction we know that
By mathematical induction we know that

for all 
Since  as
as  by
by  of Theorem 2.3, there exists a sequence
of Theorem 2.3, there exists a sequence  such that
such that  as
as  and
and  for every
for every  Hence, it follows from the definition of
Hence, it follows from the definition of  that
that

for all  This implies
This implies

for all 
In turn, it follows from (2.22) and (2.23) that

for all  , which implies that
, which implies that  is a solution of (1.5) and so the mapping
is a solution of (1.5) and so the mapping  is quadratic.
is quadratic.
By  of Theorem 2.3, we obtain
of Theorem 2.3, we obtain

which yields the inequality (2.24).
To prove the uniqueness of  , assume now that
, assume now that  is another quadratic mapping satisfying the inequality (2.24). Then
is another quadratic mapping satisfying the inequality (2.24). Then  is a fixed point of
is a fixed point of  with
with  in view of the inequality (2.24). This implies that
in view of the inequality (2.24). This implies that  and so
and so  by
by  of Theorem 2.3. The proof is complete.
of Theorem 2.3. The proof is complete.
By a similar way, one can prove the following theorem using the fixed point method.
Theorem 2.5.
Let  be a function with
be a function with  for which there exists a function
for which there exists a function  such that there exists a constant
such that there exists a constant  satisfying the inequalities
satisfying the inequalities


for all  . Then there exists a unique quadratic function
. Then there exists a unique quadratic function  defined by
defined by  such that
such that

for all 
Proof.
We use the same notations for  and
and  as in the proof of Theorem 2.4. Thus
as in the proof of Theorem 2.4. Thus  is a complete generalized metric space. Let us define an operator
is a complete generalized metric space. Let us define an operator  by
by

for all  Then it follows from (2.35) that
Then it follows from (2.35) that

for all  that is,
that is,  Thus we see that
Thus we see that  for any
for any  and so
and so  is strictly contractive with constant
is strictly contractive with constant  on
on  .
.
Next, if we put  in (2.34) and we divide both sides by
in (2.34) and we divide both sides by  , then we get by virtue of (2.35)
, then we get by virtue of (2.35)

for all  which implies
which implies  Thereafter, applying the same argument as in the proof of Theorem 2.4, we obtain the desired results.
Thereafter, applying the same argument as in the proof of Theorem 2.4, we obtain the desired results.
3. Applications of Main Results
In the following corollary, we have a stability result of (1.5) in the sense of Th. M. Rassias.
Corollary 3.1.
Let  and
and  be real numbers such that
be real numbers such that  and
and  for
for  . Assume that a function
. Assume that a function  satisfies the inequality
satisfies the inequality

for all  and for all
and for all  if
if  . Then there exists a unique quadratic function
. Then there exists a unique quadratic function  which satisfies the inequality
which satisfies the inequality

for all  and for all
and for all  if
if  . The function
. The function  is given by
is given by

for all  , where
, where  if
if  .
.
Proof.
If  , then we get
, then we get  by putting
by putting  in (3.1). Letting
in (3.1). Letting  for all
for all  and then applying Theorem 2.1 we obtain easily the desired results.
and then applying Theorem 2.1 we obtain easily the desired results.
Corollary 3.2.
Let  and
and  be real numbers such that
be real numbers such that  and
and  for
for  . Assume that a function
. Assume that a function  satisfies the inequality
satisfies the inequality

for all  . Then there exists a unique quadratic function
. Then there exists a unique quadratic function  which satisfies the inequality
which satisfies the inequality

for all  . The function
. The function  is given by
is given by

for all  .
.
In the following corollary, we have a stability result of (1.5) in the sense of Hyers.
Corollary 3.3.
Let  be a nonnegative real number. Assume that a function
be a nonnegative real number. Assume that a function  satisfies the inequality
satisfies the inequality

for all  . Then there exists a unique quadratic function
. Then there exists a unique quadratic function  , defined by
, defined by  which satisfies the inequality
which satisfies the inequality

for all  .
.
In the next corollary, we get a stability result of (1.5) in the sense of J. M. Rassias.
Corollary 3.4.
Let  be real numbers such that
be real numbers such that  and
and  , where
, where  . Suppose that a function
. Suppose that a function  satisfies
satisfies

for all  , and for all
, and for all  if
if  . Then there exists a unique quadratic function
. Then there exists a unique quadratic function  which satisfies the inequality
which satisfies the inequality

for all  and all
and all  if
if  , where
, where  if
if  .
.
Proof.
Letting  and applying Theorems 2.1 and 2.2, we get the results.
and applying Theorems 2.1 and 2.2, we get the results.
References
Ulam SM: A Collection of Mathematical Problems, Interscience Tracts in Pure and Applied Mathematics, no. 8. Interscience, New York, NY, USA; 1960:xiii+150.
Hyers DH: On the stability of the linear functional equation. Proceedings of the National Academy of Sciences of the United States of America 1941, 27: 222–224. 10.1073/pnas.27.4.222
Aoki T: On the stability of the linear transformation in Banach spaces. Journal of the Mathematical Society of Japan 1950, 2: 64–66. 10.2969/jmsj/00210064
Bourgin DG: Classes of transformations and bordering transformations. Bulletin of the American Mathematical Society 1951, 57: 223–237. 10.1090/S0002-9904-1951-09511-7
Rassias ThM: On the stability of the linear mapping in Banach spaces. Proceedings of the American Mathematical Society 1978, 72(2):297–300. 10.1090/S0002-9939-1978-0507327-1
Gajda Z: On stability of additive mappings. International Journal of Mathematics and Mathematical Sciences 1991, 14(3):431–434. 10.1155/S016117129100056X
Rassias ThM, Šemrl P: On the behavior of mappings which do not satisfy Hyers-Ulam stability. Proceedings of the American Mathematical Society 1992, 114(4):989–993. 10.1090/S0002-9939-1992-1059634-1
Găvruţa P: A generalization of the Hyers-Ulam-Rassias stability of approximately additive mappings. Journal of Mathematical Analysis and Applications 1994, 184(3):431–436. 10.1006/jmaa.1994.1211
Rassias JM: On approximation of approximately linear mappings by linear mappings. Bulletin des Sciences Mathématiques 1984, 108(4):445–446.
Rassias JM: On the stability of the non-linear Euler-Lagrange functional equation in real normed linear spaces. Journal of Mathematical and Physical Sciences 1994, 28(5):231–235.
Aczél J, Dhombres J: Functional Equations in Several Variables, Encyclopedia of Mathematics and Its Applications. Volume 31. Cambridge University Press, Cambridge, UK; 1989:xiv+462.
Hyers DH, Rassias ThM: Approximate homomorphisms. Aequationes Mathematicae 1992, 44(2–3):125–153. 10.1007/BF01830975
Skof F: Local properties and approximation of operators. Rendiconti del Seminario Matematico e Fisico di Milano 1983, 53: 113–129. 10.1007/BF02924890
Cholewa PW: Remarks on the stability of functional equations. Aequationes Mathematicae 1984, 27(1–2):76–86.
Czerwik St: On the stability of the quadratic mapping in normed spaces. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 1992, 62: 59–64. 10.1007/BF02941618
Borelli C, Forti GL: On a general Hyers-Ulam stability result. International Journal of Mathematics and Mathematical Sciences 1995, 18(2):229–236. 10.1155/S0161171295000287
I.-S. Chang and H.-M. Kim, On the Hyers-Ulam stability of quadratic functional equations, Journalof Inequalities in Pure and Applied Mathematics, vol. 3, no. 3, article 33, 12 pages, 2002.
Forti G-L: Comments on the core of the direct method for proving Hyers-Ulam stability of functional equations. Journal of Mathematical Analysis and Applications 2004, 295(1):127–133. 10.1016/j.jmaa.2004.03.011
Eshaghi Gordji M, Karimi T, Kaboli Gharetapeh S: Approximately
 -Jordan homomorphisms on Banach algebras. Journal of Inequalities and Applications 2009, 2009:-8.
-Jordan homomorphisms on Banach algebras. Journal of Inequalities and Applications 2009, 2009:-8.Eshaghi Gordji M, Zolfaghari S, Rassias JM, Savadkouhi MB: Solution and stability of a mixed type cubic and quartic functional equation in quasi-Banach spaces. Abstract and Applied Analysis 2009, 2009:-14.
Jun K-W, Kim H-M: Ulam stability problem for generalized
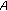 -quadratic mappings. Journal of Mathematical Analysis and Applications 2005, 305(2):466–476. 10.1016/j.jmaa.2004.10.058
-quadratic mappings. Journal of Mathematical Analysis and Applications 2005, 305(2):466–476. 10.1016/j.jmaa.2004.10.058Rassias JM: On the stability of the Euler-Lagrange functional equation. Chinese Journal of Mathematics 1992, 20(2):185–190.
Rassias JM: On the stability of the general Euler-Lagrange functional equation. Demonstratio Mathematica 1996, 29(4):755–766.
Benyamini Y, Lindenstrauss J: Geometric Nonlinear Functional Analysis. Vol. 1, American Mathematical Society Colloquium Publications. Volume 48. American Mathematical Society, Providence, RI, USA; 2000:xii+488.
Rolewicz S: Metric Linear Spaces. 2nd edition. PWN-Polish Scientific, Warsaw, Poland; 1984:xi+459.
Tabor J: Stability of the Cauchy functional equation in quasi-Banach spaces. Annales Polonici Mathematici 2004, 83(3):243–255. 10.4064/ap83-3-6
Rassias JM, Kim H-M: Generalized Hyers-Ulam stability for general additive functional equations in quasi-
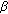 -normed spaces. Journal of Mathematical Analysis and Applications 2009, 356(1):302–309. 10.1016/j.jmaa.2009.03.005
-normed spaces. Journal of Mathematical Analysis and Applications 2009, 356(1):302–309. 10.1016/j.jmaa.2009.03.005Diaz JB, Margolis B: A fixed point theorem of the alternative, for contractions on a generalized complete metric space. Bulletin of the American Mathematical Society 1968, 74(2):305–309. 10.1090/S0002-9904-1968-11933-0
L. Cădariu and V. Radu, Fixed points and the stability of Jensen's functional equation., Journal of Inequalities in Pure and Applied Mathematics, vol. 4, no. 1, article 4, 7 pages, 2003.
Cădariu L, Radu V: Fixed points and the stability of quadratic functional equations. Analele Universităţii din Timişoara. Seria Matematică-Informatică 2003, 41(1):25–48.
Cădariu L, Radu V: On the stability of the Cauchy functional equation: a fixed point approach. In Iteration Theory (ECIT '02), Grazer Mathematische Berichte. Volume 346. Karl-Franzens-Universitaet Graz, Graz, Austria; 2004:43–52.
Hyers DH, Isac G, Rassias ThM: Topics in Nonlinear Analysis and Applications. World Scientific, River Edge, NJ, USA; 1997:xiv+699.
Isac G, Rassias ThM: Stability of
 -additive mappings: applications to nonlinear analysis. International Journal of Mathematics and Mathematical Sciences 1996, 19(2):219–228. 10.1155/S0161171296000324
-additive mappings: applications to nonlinear analysis. International Journal of Mathematics and Mathematical Sciences 1996, 19(2):219–228. 10.1155/S0161171296000324Radu V: The fixed point alternative and the stability of functional equations. Fixed Point Theory 2003, 4(1):91–96.
Jung S-M: Stability of the quadratic equation of Pexider type. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 2000, 70: 175–190. 10.1007/BF02940912
Jung S-M, Kim T-S: A fixed point approach to the stability of the cubic functional equation. Boletín de la Sociedad Mátematica Mexicana 2006, 12(1):51–57.
Jung S-M, Lee Z-H: A fixed point approach to the stability of quadratic functional equation with involution. Fixed Point Theory and Applications 2008, 2008:-11.
Jung S-M: A fixed point approach to the stability of isometries. Journal of Mathematical Analysis and Applications 2007, 329(2):879–890. 10.1016/j.jmaa.2006.06.098
Jung S-M: A fixed point approach to the stability of a Volterra integral equation. Fixed Point Theory and Applications 2007, 2007:-9.
Jung S-M, Kim T-S, Lee K-S: A fixed point approach to the stability of quadratic functional equation. Bulletin of the Korean Mathematical Society 2006, 43(3):531–541.
Jung S-M, Rassias JM: A fixed point approach to the stability of a functional equation of the spiral of Theodorus. Fixed Point Theory and Applications 2008, 2008:-7.
Acknowledgment
This work was supported by the National Research Foundation of Korea Grant funded by the Korean Government (no. 2009-0070940).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kim, HM., Kim, M. & Lee, J. Stability of Approximate Quadratic Mappings. J Inequal Appl 2010, 184542 (2010). https://doi.org/10.1155/2010/184542
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/184542
 -Jordan homomorphisms on Banach algebras. Journal of Inequalities and Applications 2009, 2009:-8.
-Jordan homomorphisms on Banach algebras. Journal of Inequalities and Applications 2009, 2009:-8.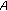 -quadratic mappings. Journal of Mathematical Analysis and Applications 2005, 305(2):466–476. 10.1016/j.jmaa.2004.10.058
-quadratic mappings. Journal of Mathematical Analysis and Applications 2005, 305(2):466–476. 10.1016/j.jmaa.2004.10.058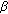 -normed spaces. Journal of Mathematical Analysis and Applications 2009, 356(1):302–309. 10.1016/j.jmaa.2009.03.005
-normed spaces. Journal of Mathematical Analysis and Applications 2009, 356(1):302–309. 10.1016/j.jmaa.2009.03.005 -additive mappings: applications to nonlinear analysis. International Journal of Mathematics and Mathematical Sciences 1996, 19(2):219–228. 10.1155/S0161171296000324
-additive mappings: applications to nonlinear analysis. International Journal of Mathematics and Mathematical Sciences 1996, 19(2):219–228. 10.1155/S0161171296000324