- Research Article
- Open access
- Published:
A System of Nonlinear Operator Equations for a Mixed Family of Fuzzy and Crisp Operators in Probabilistic Normed Spaces
Journal of Inequalities and Applications volume 2010, Article number: 152978 (2010)
Abstract
By using a random version of the theory of contractor introduced by Altman, we introduce and study a system of nonlinear operator equations for a mixed family of fuzzy and crisp operators in probabilistic normed spaces. We construct some new iterative algorithms for solving this kind of nonlinear operator equations. We also prove some new existence theorems of solutions of a new system of nonlinear operator equations for a mixed family of fuzzy and crisp operators and some new convergence results of sequences generated by iterative algorithms under joint orbitally complete conditions.
1. Introduction
Altman [1, 2] introduced the theory of contractor and contractor direction, which has a very strong significant for the study of existence and uniqueness for solving nonlinear operator equations in Banach spaces. The theory of contractor offers a unified approach to a very large class of iterative methods including the most important ones. Chang [3] introduced the concept of probabilistic contractor and studied the existence and uniqueness of solution for nonlinear operator equations with probabilistic contractor in Menger PN-spaces. By using the theory of countable extension of  -norms [4–6] and the results from [7, 8], many results for the more general classes of
-norms [4–6] and the results from [7, 8], many results for the more general classes of  -norms have been proved (see [9] and the references therein).
-norms have been proved (see [9] and the references therein).
On the other hand, since then, several kinds of variational inequalities, variational inclusions, complementarity problems, and nonlinear equations with fuzzy mappings were introduced and studied by many authors (see, e.g., [8–15]). Sharma et al. [15] considered two nonfuzzy mappings and a sequence of fuzzy mappings to define a hybrid  -compatible condition. They also showed the existence of common fixed points under such condition, where the range of the one of the two nonfuzzy mappings is joint orbitally complete. Furthermore, Cho et al. [10] introduced the concept of probabilistic contractor couple in probabilistic normed spaces and discuss the solution for nonlinear equations of fuzzy mappings and the convergence of sequences generated by the algorithms in Menger probabilistic normed spaces. Very recently, Hadžić and Pap [16] introduced some new classes of probabilistic contractions in probabilistic metric spaces. They also obtained a new fixed point theorem for the
-compatible condition. They also showed the existence of common fixed points under such condition, where the range of the one of the two nonfuzzy mappings is joint orbitally complete. Furthermore, Cho et al. [10] introduced the concept of probabilistic contractor couple in probabilistic normed spaces and discuss the solution for nonlinear equations of fuzzy mappings and the convergence of sequences generated by the algorithms in Menger probabilistic normed spaces. Very recently, Hadžić and Pap [16] introduced some new classes of probabilistic contractions in probabilistic metric spaces. They also obtained a new fixed point theorem for the  -probabilistic contraction and gave some applications to random operators.
-probabilistic contraction and gave some applications to random operators.
Motivated and inspired by the above works, in this paper, by using a random version of the theory of contractor introduced by Altman, we introduce and study a system of nonlinear operator equations for a mixed family of fuzzy and crisp operators in probabilistic normed spaces. We construct some new iterative algorithms for solving this kind of nonlinear operator equations. We also prove some new existence theorems of solution for the system of nonlinear operator equations for a mixed family of fuzzy and crisp operators and new convergence results of sequences generated by the iterative algorithms under joint orbitally complete condition. The results presented in this paper improve and generalize corresponding results of [9, 15–17].
2. Preliminaries
Let  be the set of all distribution functions
be the set of all distribution functions  such that
such that  (
( is a nondecreasing, left continuous mapping from
is a nondecreasing, left continuous mapping from  into
into  such that
such that  The special distribution function
The special distribution function  is defined by
is defined by

The ordered pair  is said to be a probabilistic metric space if
is said to be a probabilistic metric space if  is a nonempty set and
is a nonempty set and  is written by
is written by  for all
for all  satisfying the following conditions:
satisfying the following conditions:
(i) for all
for all  for all
for all 
(ii) for all
for all 
(iii) and
and  for all
for all  and
and 
A Menger space (see [18]) is a triple  where
where  is a probabilistic metric space,
is a probabilistic metric space,  is a triangular norm (abbreviated
is a triangular norm (abbreviated  -norm), and the following inequality holds:
-norm), and the following inequality holds:

Recall that a mapping  is a triangular norm (shortly, a
is a triangular norm (shortly, a  -norm) if the following conditions are satisfied:
-norm) if the following conditions are satisfied:
(i) for all
for all  ;
;
(ii) for all
for all  ;
;
(iii)if  and
and  , then
, then  for all
for all  ;
;
(iv) for all
for all  .
.
Example 2.1.
The following are the four basic examples.
(1)The minimum  -norm
-norm  is defined by
is defined by

(2)The product  -norm
-norm  is defined by
is defined by

(3)The Lukasiewicz  -norm
-norm  is defined by
is defined by

(4)The weakest  -norm, the drastic product
-norm, the drastic product  , is defined by
, is defined by

The  -topology in
-topology in  is introduced by the family of neighbourhoods
is introduced by the family of neighbourhoods  , where
, where

If a  -norm
-norm  is such that
is such that  then
then  is a metrizable topological space under the
is a metrizable topological space under the  -topology.
-topology.
Let  be a vector space over the real or complex number field
be a vector space over the real or complex number field  ,
,  , and
, and  a
a  -norm. The ordered triple
-norm. The ordered triple  is a Menger probabilistic normed space (briefly, a Menger PN-space) if and only if the following conditions are satisfied, where
is a Menger probabilistic normed space (briefly, a Menger PN-space) if and only if the following conditions are satisfied, where  for all
for all  :
:
(i) for all
for all  and
and  (
( is a neutral element for
is a neutral element for  in
in  );
);
(ii) for all
for all  and
and  (
( );
);
(iii) for all
for all  and
and  .
.
If  is a Menger PN-space and, for all
is a Menger PN-space and, for all  ,
,  is defined by
is defined by

then  is a Menger space.
is a Menger space.
The following definition can be found in [7].
Definition 2.2 (see [7]).
 is called a non-Archimedean Menger PN-space (briefly, an N.A. Menger PN-space) if
is called a non-Archimedean Menger PN-space (briefly, an N.A. Menger PN-space) if  is a Menger PN-space satisfying the following condition:
is a Menger PN-space satisfying the following condition:

If  is a Menger PN-space and
is a Menger PN-space and  is a
is a  -norm which satisfies the condition:
-norm which satisfies the condition:

then  is a Hausdorff topological vector space in the topology
is a Hausdorff topological vector space in the topology  induced by the base of neighborhoods of
induced by the base of neighborhoods of 

where 
Example 2.3 (see [9]).
It is easy to see that an ultra-metric space  belongs to the class of N.A. Menger PN-spaces, where
belongs to the class of N.A. Menger PN-spaces, where  and
and  satisfying the following conditions:
satisfying the following conditions:
(i) for all
for all  ;
;
(ii) for all
for all  ;
;
(iii) for all
for all  .
.
A fuzzy set  in
in  is a function from
is a function from  into
into  . If
. If  , then the function value
, then the function value  is called the grade of membership of
is called the grade of membership of  in
in  . The
. The  -level set of
-level set of  , denoted by
, denoted by  , is defined by
, is defined by

Let  denote the collection of all fuzzy sets
denote the collection of all fuzzy sets  in
in  such that
such that  is compact and convex for all
is compact and convex for all  and
and  . For any
. For any  ,
,  means
means  for all
for all  .
.
Let  be an arbitrary set and
be an arbitrary set and  any linear metric space. A function
any linear metric space. A function  is called fuzzy operator. Now, we define an orbit for mixed operators
is called fuzzy operator. Now, we define an orbit for mixed operators  and a joint orbitally complete space as follows.
and a joint orbitally complete space as follows.
Definition 2.4 (see [15]).
Let  be two operators from
be two operators from  into itself and
into itself and  a sequence of fuzzy operators from
a sequence of fuzzy operators from  into
into  . If, for some
. If, for some  , there exist sequences
, there exist sequences  and
and  in
in  such that
such that

then  is called an orbit for the mixed operators
is called an orbit for the mixed operators  .
.
Definition 2.5 (see [15]).
 is called
is called  -joint orbitally complete if every Cauchy sequence of each orbit at
-joint orbitally complete if every Cauchy sequence of each orbit at  is convergent in
is convergent in  .
.
Remark 2.6 (see [15]).
Clearly, if  is an any complete space and
is an any complete space and  , then
, then  is
is  -joint orbitally complete, while the converse is not necessarily true.
-joint orbitally complete, while the converse is not necessarily true.
3. Some Countable 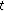 -Norms
-Norms
Let  be a
be a  -norm and, for each
-norm and, for each  , and a mapping
, and a mapping  let defined in the following way:
let defined in the following way:

A  -norm
-norm  is of
is of  -type if the family
-type if the family  is equicontinuous at
is equicontinuous at  (see [19]).
(see [19]).
Each  -norm
-norm  can be extended (by the associativity) in a unique way to the
can be extended (by the associativity) in a unique way to the  -ary operation taking the values
-ary operation taking the values  for any
for any  , which is defined by
, which is defined by

A  -norm
-norm  can be extended to countable infinitely operations taking the value
can be extended to countable infinitely operations taking the value

for any sequence  in
in  . Also, the sequence
. Also, the sequence  is nonincreasing and bounded from below and hence the limit
is nonincreasing and bounded from below and hence the limit  exists.
exists.
By (3.3) and fixed point theory in the book by Hadžić and Pap [4], it is interested to investigate the classes of  -norms
-norms  and sequences
and sequences  in the interval
in the interval  such that
such that  and
and

It is obvious that

for  and
and  .
.
The important classes of  -norms are given in the following example.
-norms are given in the following example.
Example 3.1 (see [16]).
( ) The Dombi family of
) The Dombi family of  -norms
-norms  is defined by
is defined by

( ) The Aczél-Alsina family of
) The Aczél-Alsina family of  -norms
-norms  is defined by
is defined by

( ) The family
) The family  of Sugeno-Weber
of Sugeno-Weber  -norms is given by
-norms is given by

( ) The Schweizer-Sklar family of
) The Schweizer-Sklar family of  -norms
-norms  is defined by
is defined by

The condition  is fulfilled by the families
is fulfilled by the families  ,
,  .
.
There exists a member of the family  which is incomparable with
which is incomparable with  and there exists a member of the family
and there exists a member of the family  which is incomparable with
which is incomparable with  .
.
In [4], the following results and proposition are obtained.
(1)If  is the Dombi family of
is the Dombi family of  -norms and
-norms and  is a sequence of elements from
is a sequence of elements from  such that
such that  , then we have the following equivalence:
, then we have the following equivalence:

(2)If  is the Sugeno-Weber family of
is the Sugeno-Weber family of  -norms and
-norms and  is a sequence of elements from
is a sequence of elements from  such that
such that  , then we have the following equivalence:
, then we have the following equivalence:

(3)The equivalence (3.10) holds also for the family  , that is,
, that is,

Proposition 3.2.
Let  be a sequence of numbers from
be a sequence of numbers from  such that
such that  and
and  a
a  -norm of
-norm of  -type. Then
-type. Then 
4. The Main Results
Let  be a Menger PN-space with the
be a Menger PN-space with the  -norm
-norm  satisfying condition
satisfying condition  and
and  a nonempty subset of
a nonempty subset of  . If
. If  , where
, where

then  is called a probabilistically bounded set. Let
is called a probabilistically bounded set. Let  be the collection of all nonempty closed probabilistically bounded subsets of
be the collection of all nonempty closed probabilistically bounded subsets of  . For any
. For any  , define the distribution functions
, define the distribution functions  and
and  by
by


respectively.
Let  be two fuzzy operators satisfying the following condition (I).
be two fuzzy operators satisfying the following condition (I).
(I)There exist two mappings  such that, for all
such that, for all  , the set
, the set  and
and  .
.
We note that

where  is a real number and
is a real number and  is a fuzzy set in
is a fuzzy set in  decided by the fuzzy operator
decided by the fuzzy operator  at
at  . By using each pair of fuzzy operators
. By using each pair of fuzzy operators  and
and  , we can define two set-valued mappings
, we can define two set-valued mappings  and
and  as follows:
as follows:

In the sequel, for some  ,
,  and
and  are called the set-valued mappings induced by the fuzzy mappings
are called the set-valued mappings induced by the fuzzy mappings  and
and  , respectively.
, respectively.
We need the following lemma and definitions.
Lemma 4.1 (see [7]).
Let  be a Menger PN-space with a
be a Menger PN-space with a  -norm
-norm  satisfying
satisfying  and let
and let  . Then we have the following.
. Then we have the following.
(1) .
.
(2) for all
for all  if and only if
if and only if  .
.
(3) for all
for all  with
with  .
.
(4)If  , then we have
, then we have  for all
for all 
Definition 4.2.
Let  and
and  be two Menger PN-spaces. A set-valued mapping
be two Menger PN-spaces. A set-valued mapping  is said to be
is said to be  -closed if, for any
-closed if, for any  and
and  , whenever
, whenever  and
and  , we have
, we have  and
and  .
.
Definition 4.3.
A function  is said to satisfy the condition
is said to satisfy the condition  if it is nondecreasing and
if it is nondecreasing and  for all
for all  .
.
It is easy to prove that if  satisfies the condition
satisfies the condition  , then
, then  for all
for all  .
.
Definition 4.4 (see [7]).
Let  and
and  be two Menger PN-spaces and
be two Menger PN-spaces and  ,
,  be two set-valued mappings. Let
be two set-valued mappings. Let  be two mappings, where
be two mappings, where  denotes the space of all linear operators from
denotes the space of all linear operators from  to
to  .
.  is called a probabilistic
is called a probabilistic  -contractor couple of
-contractor couple of  and
and  if there exists a function
if there exists a function  satisfying the condition
satisfying the condition  such that
such that

for all  ,
,  ,
,  and
and

for all  ,
,  , and
, and 
Now, we introduce two algorithms for our main results as follows.
Algorithm 1.
Let  be an N.A. Menger PN-space with a
be an N.A. Menger PN-space with a  -norm
-norm  and
and  be a Menger PN-space with a
be a Menger PN-space with a  -norm
-norm  . Let
. Let  ,
,  be two operators from
be two operators from  into itself,
into itself,  a sequence of fuzzy operators from
a sequence of fuzzy operators from  into
into  satisfying the condition (I), and
satisfying the condition (I), and  the
the  -closed set-valued operators induced by the fuzzy operators
-closed set-valued operators induced by the fuzzy operators  for all
for all  . Let
. Let  and
and  satisfy the condition
satisfy the condition  . Suppose that
. Suppose that
(i) and
and  for all
for all  ;
;
(ii) for all
for all  and
and  ,
,  for all
for all  and
and  ;
;
(iii) is a probabilistic
is a probabilistic  -contractor couple of
-contractor couple of  and
and  ;
;
(iv)for all  and
and  , there exists
, there exists  such that
such that

and, for all  and
and  , there exists
, there exists  such that
such that

For any  and
and  , put
, put  , where
, where  is a real number. It follows from the assumption (ii) that
is a real number. It follows from the assumption (ii) that  . Replacing
. Replacing  and
and  by
by  and
and  in (4.6), respectively, from (3.11) of Lemma 4.1, the assumption (iii), and
in (4.6), respectively, from (3.11) of Lemma 4.1, the assumption (iii), and  , it follows that
, it follows that

Since  and
and  , it follows that
, it follows that  and so
and so

Since  is left continuous, now we have
is left continuous, now we have

and so  for all
for all  In fact, if there exists
In fact, if there exists  such that
such that  , then it follows from (4.12) that
, then it follows from (4.12) that

which is a contradiction. Therefore,  for all
for all  . Thus, from (4.12), we have
. Thus, from (4.12), we have

By the assumption (iv) and (4.14), for any  , there exists
, there exists  such that
such that

Let  , where
, where  is a real number which satisfies inequality
is a real number which satisfies inequality  . By the assumption (ii), we know that
. By the assumption (ii), we know that  . Similarly, since
. Similarly, since  , it follows from (4.6) that
, it follows from (4.6) that

It is easy to check that  for all
for all  and so it follows from (4.15) that
and so it follows from (4.15) that

Now, for any  , the assumption (iv) implies that there exists
, the assumption (iv) implies that there exists  such that
such that

Inductively, we can get two sequences  in
in  and
and  in
in  , respectively, as follows:
, respectively, as follows:

where  is a real monotone decreasing sequence in
is a real monotone decreasing sequence in  and
and  as
as  the sequence
the sequence  in
in  is defined by (2.13) and satisfies the following:
is defined by (2.13) and satisfies the following:

Algorithm 2.
Let  be a N.A. Menger PN-space with a
be a N.A. Menger PN-space with a  -norm
-norm  ,
,  a Menger PN-space with a
a Menger PN-space with a  -norm
-norm  , and
, and  be two operators. Let
be two operators. Let  a sequence of fuzzy operators from
a sequence of fuzzy operators from  into
into  satisfying the condition (I) and
satisfying the condition (I) and  the set-valued operators induced by the fuzzy operators
the set-valued operators induced by the fuzzy operators  for all
for all  . Let
. Let  and
and  satisfy the condition
satisfy the condition  . Suppose that the conditions (ii)–(iv) in Algorithm 1 are satisfied. If
. Suppose that the conditions (ii)–(iv) in Algorithm 1 are satisfied. If
 and
and  for all
for all  , then, for any
, then, for any  and
and  , we have two sequences
, we have two sequences  in
in  and
and  in
in  , respectively, defined as follows:
, respectively, defined as follows:

where the sequence  in
in  is defined by (2.13).
is defined by (2.13).
Now, we state our main results by using the similar ideas as in [9].
Theorem 4.5.
Let  be an N.A. Menger PN-space with a t-norm
be an N.A. Menger PN-space with a t-norm  and
and  be a Menger PN-space with a t-norm
be a Menger PN-space with a t-norm  . Let
. Let  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  be the same as in Algorithm 1. Suppose that the conditions (i)–(iv) in Algorithm 1 hold and the following conditions are satisfied:
be the same as in Algorithm 1. Suppose that the conditions (i)–(iv) in Algorithm 1 hold and the following conditions are satisfied:
 is
is  -joint orbitally complete for some
-joint orbitally complete for some  ;
;
there exists a constant  such that, for any constant
such that, for any constant  ,
,

there exist  and
and  such that the
such that the  -norm
-norm  satisfies the following condition:
satisfies the following condition:

where  is a real nonnegative number.
is a real nonnegative number.
Then the following system of nonlinear operator equations:

has a solution  such that
such that  . Further,
. Further,  -converges to a solution of (4.24) and
-converges to a solution of (4.24) and  -converges to
-converges to  , where
, where  in
in  and
and  in
in  are two sequences generated by Algorithm 1.
are two sequences generated by Algorithm 1.
Proof.
By (4.19), (4.20), and the assumption (vi), since  is a monotone decreasing sequence with
is a monotone decreasing sequence with  , we have
, we have

which imply that

Since  is N.A. Menger PN-space, it follows from (4.26) that, for any positive integers
is N.A. Menger PN-space, it follows from (4.26) that, for any positive integers 
 ,
,

Since  , it follows that, for all
, it follows that, for all  and
and  , there exists a positive integer
, there exists a positive integer  such that, for all
such that, for all  and
and  ,
,

and so

Hence  is a
is a  -Cauchy sequence in
-Cauchy sequence in  . Since
. Since  is
is  -joint orbitally complete, we can assume that
-joint orbitally complete, we can assume that  Moreover, by (4.20), it is easy to see that
Moreover, by (4.20), it is easy to see that  for all
for all  and so
and so  . Since
. Since  and
and  are
are  -closed, it follows from (4.19) and the assumption (i) that
-closed, it follows from (4.19) and the assumption (i) that

that is,  is a solution of (4.24) and
is a solution of (4.24) and  . This completes the proof.
. This completes the proof.
From Theorem 4.5, we have the following.
Corollary 4.6.
Let  be an N.A. Menger PN-space with a t-norm
be an N.A. Menger PN-space with a t-norm  and
and  a Menger PN-space with a
a Menger PN-space with a  -norm
-norm  . Let
. Let  ,
,  be two operators from
be two operators from  into itself,
into itself,  a sequence of fuzzy operators from
a sequence of fuzzy operators from  into
into  satisfying the condition (I), and
satisfying the condition (I), and  the
the  -closed set-valued operators induced by the fuzzy operators
-closed set-valued operators induced by the fuzzy operators  for all
for all  . Let
. Let  and
and  satisfy the condition
satisfy the condition  . Suppose that the conditions (i)-(iv) in Algorithm 1 and (v)-(vi) in Theorem 4.5 are satisfied. If
. Suppose that the conditions (i)-(iv) in Algorithm 1 and (v)-(vi) in Theorem 4.5 are satisfied. If  -norm
-norm  is of
is of  -type, then the conclusions of Theorem 4.5 still hold.
-type, then the conclusions of Theorem 4.5 still hold.
Proof.
By Proposition 3.2, we know that all the conditions of Theorem 4.5 are satisfied. Thus the conclusions of Theorem 4.5 still hold.
Corollary 4.7.
Let  for some
for some  be a N.A. Menger PN-space and
be a N.A. Menger PN-space and  be a Menger PN-space. Let
be a Menger PN-space. Let  ,
,  be two operators from
be two operators from  into itself,
into itself,  be a sequence of fuzzy operators from
be a sequence of fuzzy operators from  into
into  satisfying the condition (I) and
satisfying the condition (I) and  be the
be the  -closed set-valued operators induced by the fuzzy operators
-closed set-valued operators induced by the fuzzy operators  for all
for all  . Let
. Let  and
and  satisfy the condition
satisfy the condition  . Suppose that the conditions (i)–(iv) in Algorithm 1 and (v)-(vi) of Theorem 4.5 are satisfied. If there exist
. Suppose that the conditions (i)–(iv) in Algorithm 1 and (v)-(vi) of Theorem 4.5 are satisfied. If there exist  and
and  for some
for some  such that
such that  for all
for all  , where
, where  is a constant, then the conclusions of Theorem 4.5 still hold.
is a constant, then the conclusions of Theorem 4.5 still hold.
Proof.
From the equivalence (3.10), we have

Corollary 4.8.
Let  for some
for some  be an N.A. Menger PN-space. Let
be an N.A. Menger PN-space. Let  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  be the same as in Theorem 4.5. Suppose that the conditions (i)–(iv) in Algorithm 1 and (v)-(vi) in Theorem 4.5 are satisfied. If there exist
be the same as in Theorem 4.5. Suppose that the conditions (i)–(iv) in Algorithm 1 and (v)-(vi) in Theorem 4.5 are satisfied. If there exist  and
and  for some
for some  such that
such that  for all
for all  , where
, where  is a constant, then the conclusions of Theorem 4.5 still hold.
is a constant, then the conclusions of Theorem 4.5 still hold.
Proof.
From the equivalence (3.11), we have

Remark 4.9.
Since

it is easy to see that Corollary 4.8 is a generalization of the corresponding result in Fang [9].
Corollary 4.10.
Let  for some
for some  be an N.A. Menger PN-space with a
be an N.A. Menger PN-space with a  -norm
-norm  . Let
. Let  ,
,  ,
,  ,
,  ,
, ,
,  ,
,  , and
, and  be the same as in Theorem 4.5. Suppose that the conditions (i)–(iv) in Algorithm 1 and (v)-(vi) of Theorem 4.5 are satisfied. If there exist
be the same as in Theorem 4.5. Suppose that the conditions (i)–(iv) in Algorithm 1 and (v)-(vi) of Theorem 4.5 are satisfied. If there exist  and
and  for some
for some  such that
such that  for all
for all  , where
, where  is a constant, then the conclusions of Theorem 4.5 still hold.
is a constant, then the conclusions of Theorem 4.5 still hold.
Proof.
From the equivalence (3.12), we have

Corollary 4.11.
Let  be an N.A. Menger PN-space and
be an N.A. Menger PN-space and  satisfy the following condition:
satisfy the following condition:

where a mapping  satisfies the condition
satisfies the condition  . Suppose that the conditions (i) in Algorithm 1 and (v) in Theorem 4.5 are satisfied and there exists
. Suppose that the conditions (i) in Algorithm 1 and (v) in Theorem 4.5 are satisfied and there exists  and
and  such that
such that  -norm
-norm  satisfies the following condition:
satisfies the following condition:

and, for all  and
and  , there exists
, there exists  such that
such that

Then there exists a point  such that
such that  , that is,
, that is,  is a fixed point of
is a fixed point of  .
.
Proof.
Putting  for any fixed
for any fixed  and
and  , the mappings
, the mappings  and
and  satisfy all the hypotheses of Theorem 4.5. Therefore, there exists a point
satisfy all the hypotheses of Theorem 4.5. Therefore, there exists a point  such that
such that  , which means that
, which means that  is a fixed point of
is a fixed point of  . This completes the proof.
. This completes the proof.
Theorem 4.12.
Let  be an N.A. Menger PN-space with a
be an N.A. Menger PN-space with a  -norm
-norm  and
and  be a Menger PN-space with a
be a Menger PN-space with a  -norm
-norm  . Let
. Let  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  be the same as in Algorithm 2. Suppose that the conditions (ii)–(iv) in Algorithm 1 and
be the same as in Algorithm 2. Suppose that the conditions (ii)–(iv) in Algorithm 1 and  in Algorithm 2 are satisfied. If
in Algorithm 2 are satisfied. If
 is
is  -joint orbitally complete for some
-joint orbitally complete for some  ,
,
there exists a constant  such that
such that

there exist  and
and  such that the
such that the  -norm
-norm  satisfies the following condition:
satisfies the following condition:

then the following system of nonlinear operator equations:

has a solution  such that
such that  . Further,
. Further,  -converges to a solution of (4.40) and
-converges to a solution of (4.40) and  -converges to
-converges to  , where the sequences
, where the sequences  in
in  and
and  in
in  are defined by Algorithm 2.
are defined by Algorithm 2.
Proof.
Let  and
and  for all
for all  . It is obvious that all the conditions of Theorem 4.5 are satisfied. Therefore, the conclusion of Theorem 4.12 follows from Theorem 4.5 immediately.
. It is obvious that all the conditions of Theorem 4.5 are satisfied. Therefore, the conclusion of Theorem 4.12 follows from Theorem 4.5 immediately.
Remark 4.13.
Similarly, we can obtain the conclusions of Theorem 4.12 if we replace the condition (iii) in Theorem 4.12 by the corresponding condition in Proposition 3.2 and the equivalences (3.10)–(3.12), respectively.
References
Altman M: Contractors and Contractor Directions. Theory and Applications. Marcel Dekker, New York, NY, USA; 1977:x+290.
Altman M: Contractors and fixed points. In Topological Methods in Nonlinear Functional Analysis, Contemporary Mathematics. Volume 21. American Mathematical Society, Providence, RI, USA; 1983:1–14.
Chang SS: Probabilistic contractor and the solutions for lonlinear equations in PN-spaces. Chinese Science Bulletin 1990, 35: 1451–1454.
Hadžić O, Pap E: Fixed Point Theory in Probabilistic Metric Spaces, Theory in Probabilistic Metric Spaces. Volume 536. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2001:x+273.
Hadžić O, Pap E, Budinčević M: Countable extension of triangular norms and their applications to the fixed point theory in probabilistic metric spaces. Kybernetika 2002, 38(3):363–381.
Klement EP, Mesiar R, Pap E: Triangular Norms, Trends in Logic—Studia Logica Library. Volume 8. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2000:xx+385.
Chang S-S, Cho YJ, Kang SM: Nonlinear Operator Theory in Probabilistic Metric Spaces. Nova Science, Huntington, NY, USA; 2001:x+338.
Žikić T: Existence of fixed point in fuzzy structures, Ph.D. thesis. Faculty of Science and Mathematics, University of Novi Sad, Vojvodina, Serbia; 2002.
Fang J-X: On nonlinear equations for fuzzy mappings in probabilistic normed spaces. Fuzzy Sets and Systems 2002, 131(3):357–364. 10.1016/S0165-0114(01)00214-7
Cho YJ, Huang NJ, Kang SM: Nonlinear equations for fuzzy mappings in probabilistic normed spaces. Fuzzy Sets and Systems 2000, 110(1):115–122. 10.1016/S0165-0114(98)00009-8
Huang N-J: Completely generalized strongly nonlinear quasi-complementarity problems for fuzzy mappings. Indian Journal of Pure and Applied Mathematics 1997, 28(1):23–32.
Huang N-J: Random generalized nonlinear variational inclusions for random fuzzy mappings. Fuzzy Sets and Systems 1999, 105(3):437–444. 10.1016/S0165-0114(97)00222-4
Huang N-J, Lan H-Y: A couple of nonlinear equations with fuzzy mappings in fuzzy normed spaces. Fuzzy Sets and Systems 2005, 152(2):209–222. 10.1016/j.fss.2004.11.010
Lee BS, Cho SJ: A fixed point theorem for contractive-type fuzzy mappings. Fuzzy Sets and Systems 1994, 61(3):309–312. 10.1016/0165-0114(94)90173-2
Sharma BK, Sahu DR, Bounias M: Common fixed point theorems for a mixed family of fuzzy and crisp mappings. Fuzzy Sets and Systems 2002, 125(2):261–268. 10.1016/S0165-0114(01)00053-7
Hadžić O, Pap E: New classes of probabilistic contractions and applications to random operators. In Fixed Point Theory and Applications. Volume 4. Edited by: Cho YJ, Kim JK, Kang SM. Nova Science, Hauppauge, NY, USA; 2003:97–119.
Bounias M: A theorem proving the irreversibility of the biological arrow of time based on fixed points in the brain as a compact and -complete topological space. In Computing Anticipatory Systems, AIP Conference Proceedings. Volume 517. American Institute of Physics; 2000:233–243.
Schweizer B, Sklar A: Probabilistic Metric Spaces, North-Holland Series in Probability and Applied Mathematics. North-Holland, New York, NY, USA; 1983:xvi+275.
Hadžić O: A fixed point theorem in Menger spaces. Publications de l'Institut Mathématique 1979, 26: 107–112.
Acknowledgments
This work was supported by the Korea Research Foundation Grant funded by the Korean Government (KRF-2008-313-C00050), the Sichuan Youth Science and Technology Foundation (08ZQ026-008), and the Open Foundation of Artificial Intelligence of Key Laboratory of Sichuan Province (2009RZ001).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cho, Y., Lan, Hy. & Huang, Nj. A System of Nonlinear Operator Equations for a Mixed Family of Fuzzy and Crisp Operators in Probabilistic Normed Spaces. J Inequal Appl 2010, 152978 (2010). https://doi.org/10.1155/2010/152978
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/152978
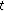 -Norms
-Norms