- Research Article
- Open access
- Published:
Almost Sure Central Limit Theorem for a Nonstationary Gaussian Sequence
Journal of Inequalities and Applications volume 2010, Article number: 130915 (2010)
Abstract
Let  be a standardized non-stationary Gaussian sequence, and let denote
be a standardized non-stationary Gaussian sequence, and let denote  ,
,  . Under some additional condition, let the constants
. Under some additional condition, let the constants  satisfy
satisfy  as
as  for some
for some  and
and  , for some
, for some  , then, we have
, then, we have  almost surely for any
almost surely for any  , where
, where  is the indicator function of the event
is the indicator function of the event  and
and  stands for the standard normal distribution function.
stands for the standard normal distribution function.
1. Introduction
When  is a sequence of independent and identically distributed (i.i.d.) random variables and
is a sequence of independent and identically distributed (i.i.d.) random variables and  for
for  . If
. If  , the so-called almost sure central limit theorem (ASCLT) has the simplest form as follows:
, the so-called almost sure central limit theorem (ASCLT) has the simplest form as follows:

almost surely for all  , where
, where  is the indicator function of the event
is the indicator function of the event  and
and  stands for the standard normal distribution function. This result was first proved independently by Brosamler [1] and Schatte [2] under a stronger moment condition; since then, this type of almost sure version was extended to different directions. For example, Fahrner and Stadtmüller [3] and Cheng et al. [4] extended this almost sure convergence for partial sums to the case of maxima of i.i.d. random variables. Under some natural conditions, they proved as follows:
stands for the standard normal distribution function. This result was first proved independently by Brosamler [1] and Schatte [2] under a stronger moment condition; since then, this type of almost sure version was extended to different directions. For example, Fahrner and Stadtmüller [3] and Cheng et al. [4] extended this almost sure convergence for partial sums to the case of maxima of i.i.d. random variables. Under some natural conditions, they proved as follows:

for all  , where
, where  and
and  satisfy
satisfy

for any continuity point  of
of  .
.
In a related work, Csáki and Gonchigdanzan [5] investigated the validity of (1.2) for maxima of stationary Gaussian sequences under some mild condition whereas Chen and Lin [6] extended it to non-stationary Gaussian sequences. Recently, Dudziński [7] obtained two-dimensional version for a standardized stationary Gaussian sequence. In this paper, inspired by the above results, we further study ASCLT in the joint version for a non-stationary Gaussian sequence.
2. Main Result
Throughout this paper, let  be a non-stationary standardized normal sequence, and
be a non-stationary standardized normal sequence, and  . Here
. Here  and
and  stand for
stand for  and
and  , respectively.
, respectively.  is the standard normal distribution function, and
is the standard normal distribution function, and  is its density function;
is its density function;  will denote a positive constant although its value may change from one appearance to the next. Now, we state our main result as follows.
will denote a positive constant although its value may change from one appearance to the next. Now, we state our main result as follows.
Theorem 2.1.
Let  be a sequence of non-stationary standardized Gaussian variables with covariance matrix
be a sequence of non-stationary standardized Gaussian variables with covariance matrix  such that
such that  for
for  , where
, where  for all
for all  and
and  . If the constants
. If the constants  satisfy
satisfy  as
as  for some
for some  and
and  , for some
, for some  , then
, then

almost surely for any  .
.
Remark 2.2.
The condition  is inspired by (a1) in Dudziński [8], which is much more weaker.
is inspired by (a1) in Dudziński [8], which is much more weaker.
3. Proof
First, we introduce the following lemmas which will be used to prove our main result.
Lemma 3.1.
Under the assumptions of Theorem 2.1, one has

Proof.
This lemma comes from Chen and Lin [6].
The following lemma is Theorem 2.1 and Corollary  in Li and Shao [9].
in Li and Shao [9].
Lemma 3.2.
-
(1)
Let
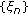 and
and  be sequences of standard Gaussian variables with covariance matrices
be sequences of standard Gaussian variables with covariance matrices  and
and 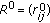 , respectively. Put
, respectively. Put 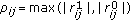 . Then one has
. Then one has 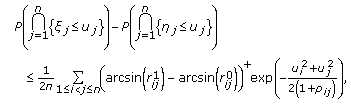 (3.2)
(3.2)
for any real numbers  ,
,  .
.
-
(2)
Let
 be standard Gaussian variables with
be standard Gaussian variables with  . Then
. Then 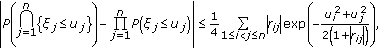 (3.3)
(3.3)
for any real numbers  ,
,  .
.
Lemma 3.3.
Let  be a sequence of standard Gaussian variables and satisfy the conditions of Theorem 2.1, then for
be a sequence of standard Gaussian variables and satisfy the conditions of Theorem 2.1, then for  , one has
, one has

for any  .
.
Proof.
By the conditions of Theorem 2.1, we have

then, for  , by
, by  , it follows that
, it follows that

Then, there exist numbers  ,
,  , such that, for any
, such that, for any  , we have
, we have

We can write that

where  is a random variable, which has the same distribution as
is a random variable, which has the same distribution as  , but it is independent of
, but it is independent of  For
For  apply Lemma 3.2 (1) with
apply Lemma 3.2 (1) with  Then
Then  for
for  and
and  for
for  . Thus, we have (for
. Thus, we have (for  )
)

Since (3.5), (3.7) hold, we obtain

Now define  by
by  . By the well-known fact
. By the well-known fact

it is easy to see that

Thus, according to the assumption  , we have
, we have  for some
for some  . Hence
. Hence

Now, we are in a position to estimate  . Observe that
. Observe that

For  , it follows that
, it follows that

By Lemma 3.2 (2), we have

Thus by Lemma 3.1 we obtain the desired result.
Lemma 3.4.
Let  be a sequence of standard Gaussian variables satisfying the conditions of Theorem 2.1, then for
be a sequence of standard Gaussian variables satisfying the conditions of Theorem 2.1, then for  , any
, any  , one has
, one has

Proof.
Apply Lemma 3.2 (1) with ( ,
,  ,
,  ,
,  ,
,  ,
,  ), (
), ( ), where
), where  has the same distribution as
has the same distribution as  , but it is independent of
, but it is independent of  . Then,
. Then,

Thus, combined with (3.5), (3.7), it follows that

Using Lemma 3.1, we have

By the similar technique that was applied to prove (3.10), we obtain

For  , by
, by  , and (3.12), we have
, and (3.12), we have

As to  , by (3.5) and (3.6), we have
, by (3.5) and (3.6), we have

Thus the proof of this lemma is completed.
Proof of Theorem 2.1.
First, by assumptions and Theorem  in Leadbetter et al. [10], we have
in Leadbetter et al. [10], we have

Let  denote a random variable which has the same distribution as
denote a random variable which has the same distribution as  , but it is independent of
, but it is independent of  then by (3.10), we derive
then by (3.10), we derive

Thus, by the standard normal property of  , we have
, we have

Hence, to complete the proof, it is sufficient to show

In order to show this, by Lemma 3.1 in Csáki and Gonchigdanzan [5], we only need to prove

for  and any
and any  . Let
. Let  . Then
. Then

Since  , it follows that
, it follows that

Now, we turn to estimate  . Observe that for
. Observe that for 

By Lemma 3.3, we have

Using Lemma 3.4, it follows that

Hence for  , we have
, we have

Consequently

Thus, we complete the proof of (3.28) by (3.30) and (3.35). Further, our main result is proved.
References
Brosamler GA: An almost everywhere central limit theorem. Mathematical Proceedings of the Cambridge Philosophical Society 1988, 104(3):561–574. 10.1017/S0305004100065750
Schatte P: On strong versions of the central limit theorem. Mathematische Nachrichten 1988, 137: 249–256. 10.1002/mana.19881370117
Fahrner I, Stadtmüller U: On almost sure max-limit theorems. Statistics & Probability Letters 1998, 37(3):229–236. 10.1016/S0167-7152(97)00121-1
Cheng S, Peng L, Qi Y: Almost sure convergence in extreme value theory. Mathematische Nachrichten 1998, 190: 43–50. 10.1002/mana.19981900104
Csáki E, Gonchigdanzan K: Almost sure limit theorems for the maximum of stationary Gaussian sequences. Statistics & Probability Letters 2002, 58(2):195–203. 10.1016/S0167-7152(02)00128-1
Chen S, Lin Z: Almost sure max-limits for nonstationary Gaussian sequence. Statistics & Probability Letters 2006, 76(11):1175–1184. 10.1016/j.spl.2005.12.018
Dudziński M: The almost sure central limit theorems in the joint version for the maxima and sums of certain stationary Gaussian sequences. Statistics & Probability Letters 2008, 78(4):347–357. 10.1016/j.spl.2007.07.007
Dudziński M: An almost sure limit theorem for the maxima and sums of stationary Gaussian sequences. Probability and Mathematical Statistics 2003, 23(1):139–152.
Li WV, Shao Q: A normal comparison inequality and its applications. Probability Theory and Related Fields 2002, 122(4):494–508. 10.1007/s004400100176
Leadbetter MR, Lindgren G, Rootzén H: Extremes and Related Properties of Random Sequences and Processes, Springer Series in Statistics. Springer, New York, NY, USA; 1983:xii+336.
Acknowledgments
The author thanks the referees for pointing out some errors in a previous version, as well as for several comments that have led to improvements in this paper. The authors would like to thank Professor Zuoxiang Peng of Southwest University in China for his help. The paper has been supported by the young excellent talent foundation of Huaiyin Normal University.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zang, Qp. Almost Sure Central Limit Theorem for a Nonstationary Gaussian Sequence. J Inequal Appl 2010, 130915 (2010). https://doi.org/10.1155/2010/130915
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/130915
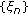 and
and  be sequences of standard Gaussian variables with covariance matrices
be sequences of standard Gaussian variables with covariance matrices  and
and 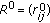 , respectively. Put
, respectively. Put 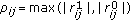 . Then one has
. Then one has 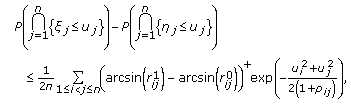
 be standard Gaussian variables with
be standard Gaussian variables with  . Then
. Then