- Research Article
- Open access
- Published:
A-Harmonic Equations and the Dirac Operator
Journal of Inequalities and Applications volume 2010, Article number: 124018 (2010)
Abstract
We show how  -harmonic equations arise as components of Dirac systems. We generalize
-harmonic equations arise as components of Dirac systems. We generalize  -harmonic equations to
-harmonic equations to  -Dirac equations. Removability theorems are proved for solutions to
-Dirac equations. Removability theorems are proved for solutions to  -Dirac equations.
-Dirac equations.
1. Introduction
This paper explains how  -harmonic equations arise from Dirac systems. Indeed the main purpose of this paper is to elucidate the connection between the theories of
-harmonic equations arise from Dirac systems. Indeed the main purpose of this paper is to elucidate the connection between the theories of  -harmonic functions and Dirac analysis. An
-harmonic functions and Dirac analysis. An  -harmonic equation
-harmonic equation  is a component of a Dirac system
is a component of a Dirac system

This component is the scalar (real) part of the Dirac system, under appropriate identifications. Hence any real-valued solution to the Dirac system is an  -harmonic function. As such, the class of
-harmonic function. As such, the class of  -harmonic functions which are also solutions of the Dirac system are a special class of
-harmonic functions which are also solutions of the Dirac system are a special class of  -harmonic functions. See Section 3 for a detailed discussion. As an application, we show that a result concerning removable singularities for
-harmonic functions. See Section 3 for a detailed discussion. As an application, we show that a result concerning removable singularities for  -harmonic functions satisfying a Lipschitz condition or of bounded mean oscillation extends to Clifford valued solutions to corresponding Dirac equations. The result also holds for functions of a certain order of growth. This seems to be new even in the case of an
-harmonic functions satisfying a Lipschitz condition or of bounded mean oscillation extends to Clifford valued solutions to corresponding Dirac equations. The result also holds for functions of a certain order of growth. This seems to be new even in the case of an  -harmonic function.
-harmonic function.
In Section 2, we present preliminaries about Clifford algebra along with definitions and notations. In Section 3, we introduce  -Dirac equations and show the correspondence with
-Dirac equations and show the correspondence with  -harmonic equations. The Caccioppoli estimate for solutions to
-harmonic equations. The Caccioppoli estimate for solutions to  -Dirac equations appears in Section 4 and the removability theorems are in Section 5 along with references. For other recent work on nonlinear Dirac equations, see [1–6].
-Dirac equations appears in Section 4 and the removability theorems are in Section 5 along with references. For other recent work on nonlinear Dirac equations, see [1–6].
2. Preliminaries
We write  for the real universal Clifford algebra over
for the real universal Clifford algebra over  The Clifford algebra is generated over
The Clifford algebra is generated over  by the basis of reduced products
by the basis of reduced products

where  is an orthonormal basis of
is an orthonormal basis of  with the relation
with the relation  We write
We write  for the identity. The dimension of
for the identity. The dimension of  is
is  . We have an increasing tower
. We have an increasing tower  The Clifford algebra
The Clifford algebra  is a graded algebra as
is a graded algebra as 
 , where
, where  are those elements whose reduced Clifford products have length
are those elements whose reduced Clifford products have length 
For  ,
,  denotes the scalar part of
denotes the scalar part of  , that is, the coefficient of the element
, that is, the coefficient of the element  .
.
Throughout,  is a connected and open set with boundary
is a connected and open set with boundary  . A Clifford-valued function
. A Clifford-valued function  can be written as
can be written as  where each
where each  is real-valued and
is real-valued and are reduced products. The norm used here is given by
are reduced products. The norm used here is given by  This norm is submultiplicative,
This norm is submultiplicative,  .
.
The Dirac operator used here is as follows:

Also  Here
Here  is the Laplace operator which operates only on coefficients. A function is monogenic when
is the Laplace operator which operates only on coefficients. A function is monogenic when 
Throughout,  is a cube in
is a cube in  with volume
with volume  . We write
. We write  for the cube with the same center as
for the cube with the same center as  and with sidelength
and with sidelength  times that of
times that of  . For
. For  , we write
, we write  for the space of Clifford-valued functions in
for the space of Clifford-valued functions in  whose coefficients belong to the usual
whose coefficients belong to the usual  space. Also,
space. Also,  is the space of Clifford valued functions in
is the space of Clifford valued functions in  whose coefficients as well as their first distributional derivatives are in
whose coefficients as well as their first distributional derivatives are in  . We also write
. We also write  for
for  , where the intersection is over all
, where the intersection is over all  compactly contained in
compactly contained in  We similarly write
We similarly write  Moreover, we write
Moreover, we write  for the space of monogenic functions in
for the space of monogenic functions in 
Furthermore, we define the Dirac Sobolev space

The local space  is similarly defined. Notice that if
is similarly defined. Notice that if  is monogenic, then
is monogenic, then  if and only if
if and only if  Also it is immediate that
Also it is immediate that 
3. Correspondence and the 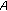 -Dirac Equation
-Dirac Equation
We first define the  -harmonic equation. We define operators
-harmonic equation. We define operators

Here  is measurable for all
is measurable for all  , and
, and  is continuous for a.e.
is continuous for a.e.  We assume the structure conditions with
We assume the structure conditions with  :
:

for some  The exponent
The exponent  will represent this exponent throughout.
will represent this exponent throughout.
An  -harmonic function,
-harmonic function,  , is a weak solution to
, is a weak solution to  , when
, when

for all  with compact support.
with compact support.
See [7] for the theory of  -harmonic equations.
-harmonic equations.
To connect these equations with Dirac systems, we define the linear isomorphism  by
by

It follows that for a real-valued function  , we have
, we have  , and for
, and for  , we have
, we have


Next we define  by
by

In this way, we see that (3.3) is equivalent to

This motivates the following definition for Dirac systems of higher-order Clifford valued functions. We use the Clifford conjugation  The product
The product  defines a Clifford-valued inner product.
defines a Clifford-valued inner product.
Moreover, the scalar part of this Clifford inner product  is the usual inner product in
is the usual inner product in  ,
,  when
when  and
and  are identified as vectors. We continue to use the Clifford notation for this scalar product. This conjugation compensates for the minus sign in (3.5) and in higher-order Clifford products. Moreover, the conjugation can be incorporated into an integration by parts formula.
are identified as vectors. We continue to use the Clifford notation for this scalar product. This conjugation compensates for the minus sign in (3.5) and in higher-order Clifford products. Moreover, the conjugation can be incorporated into an integration by parts formula.
To this purpose (we are replacing  with
with  for convenience) we recast the structure equations above and define operators:
for convenience) we recast the structure equations above and define operators:

We assume that  preserves the grading of the Clifford algebra. Here
preserves the grading of the Clifford algebra. Here  is measurable for all
is measurable for all  , and
, and  is continuous for a.e.
is continuous for a.e.  We assume the structure conditions with
We assume the structure conditions with  :
:


for some 
Definition 3.1.
A Clifford valued function  , for
, for  is a weak solution to
is a weak solution to

if for all  with compact support we have
with compact support we have

Notice that when  is the identity, then (3.13) is the Clifford Laplacian. Moreover these equations generalize the important case of the
is the identity, then (3.13) is the Clifford Laplacian. Moreover these equations generalize the important case of the  -Dirac equation:
-Dirac equation:

Here 
These equations were introduced and their conformal invariance was studied in [8].
In the case of the  -Dirac equation,
-Dirac equation,  , when
, when  , and
, and  ,
,  , are solutions to (3.13). Notice that a monogenic function
, are solutions to (3.13). Notice that a monogenic function  is trivially a solution to (3.13) and if
is trivially a solution to (3.13) and if  is a solution to (3.13), then so is
is a solution to (3.13), then so is  for any monogenic function
for any monogenic function 
In the case that  is a real-valued function
is a real-valued function  also implies that
also implies that

where  So in this case (3.13) can be identified with the two equations
So in this case (3.13) can be identified with the two equations

Hence when  is a function, (3.13) implies that
is a function, (3.13) implies that  is a harmonic field and locally there exists a harmonic function
is a harmonic field and locally there exists a harmonic function  such that
such that  If
If  is invertible, then
is invertible, then  Hence regularity of
Hence regularity of  implies regularity of the solution
implies regularity of the solution  . Notice that if
. Notice that if  , then
, then  , where
, where 
In general,  -harmonic functions do not have such regularity. This suggests the study of the scalar part of the system equation (3.13) in general. Indeed a Caccioppoli estimate holds for solutions to the scalar part of (3.13). This is the topic of the next section.
-harmonic functions do not have such regularity. This suggests the study of the scalar part of the system equation (3.13) in general. Indeed a Caccioppoli estimate holds for solutions to the scalar part of (3.13). This is the topic of the next section.
Hence we see a special class of  -harmonic functions, namely, real-valued solutions to the system (3.13). This class should have special properties.
-harmonic functions, namely, real-valued solutions to the system (3.13). This class should have special properties.
On the other hand, results about  -harmonic functions suggest possible properties of general solutions to (3.13). In this paper, we present one such extension, that of removable sets. The essential ingredient in the proof is the Caccioppoli estimate.
-harmonic functions suggest possible properties of general solutions to (3.13). In this paper, we present one such extension, that of removable sets. The essential ingredient in the proof is the Caccioppoli estimate.
4. A Caccioppoli Estimate
Next is a Caccioppoli estimate for solutions to (3.13). This result appears in [9]. We give the short proof here for completeness.
Theorem 4.1.
Let  be a solution to scalar part of (3.13) and
be a solution to scalar part of (3.13) and  ,
,  Then
Then

Proof.
Choose  . Then
. Then  Hence using (3.13) and (3.10),
Hence using (3.13) and (3.10),

Using Hölder's inequality and (3.11), we have

Corollary 4.2.
Suppose that  is a solution to (3.13). Let
is a solution to (3.13). Let  be a cube with
be a cube with  where
where  . Then there is a constant
. Then there is a constant  , independent of
, independent of  , such that
, such that

Proof.
Choose  ,
,  ,
,  in
in  and
and  .
.
5. Removability
For monogenic functions with modulus of continuity  , sets of
, sets of  -Hausdorff measure are removable [1]. For Hölder continuous analytic functions, see [10]. Sets satisfying a certain geometric condition related to Minkowski dimension are shown to be removable for
-Hausdorff measure are removable [1]. For Hölder continuous analytic functions, see [10]. Sets satisfying a certain geometric condition related to Minkowski dimension are shown to be removable for  -harmonic functions in Hölder and bounded mean oscillation classes in [11]. In the case of Hölder continuity, this was sharped in [12] to a precise condition for removable sets for
-harmonic functions in Hölder and bounded mean oscillation classes in [11]. In the case of Hölder continuity, this was sharped in [12] to a precise condition for removable sets for  -harmonic functions in terms of Hausdorff dimension.
-harmonic functions in terms of Hausdorff dimension.
We show here that sets satisfying a generalized Minkowski-type inequality, similar to that in [11], are removable for solutions to the  -Dirac equation which satisfy a certain oscillation condition. The following definition is motivated by the fact that real-valued functions satisfying various regularity properties are characterized by this definition. We explain below.
-Dirac equation which satisfy a certain oscillation condition. The following definition is motivated by the fact that real-valued functions satisfying various regularity properties are characterized by this definition. We explain below.
Definition 5.1.
Assume that  ,
,  and that
and that 
We say that  is of
is of  -oscillation in
-oscillation in  when
when

The infimum over monogenic functions is natural since they are trivially solutions to an  -Dirac equation just as constants are solutions to an
-Dirac equation just as constants are solutions to an  -harmonic equation. If
-harmonic equation. If  is a function and
is a function and  , then (5.1) is equivalent to the usual definition of the bounded mean oscillation when
, then (5.1) is equivalent to the usual definition of the bounded mean oscillation when  and (5.1) is equivalent to the usual local Lipschitz condition when
and (5.1) is equivalent to the usual local Lipschitz condition when  [13]. Moreover, at least when
[13]. Moreover, at least when  is a solution to an
is a solution to an  -harmonic equation, (5.1) is equivalent to a local order of growth condition when
-harmonic equation, (5.1) is equivalent to a local order of growth condition when  ; see [9, 14]. In these cases, the supremum is finite if we choose
; see [9, 14]. In these cases, the supremum is finite if we choose  to be the average value of the function
to be the average value of the function  over the cube
over the cube  . It is easy to see that in condition (5.1) the expansion factor "2" can be replaced by any factor greater than 1.
. It is easy to see that in condition (5.1) the expansion factor "2" can be replaced by any factor greater than 1.
If the coefficients of an  -Dirac solution
-Dirac solution  are of bounded mean oscillation, local Hölder continuous, or of a certain local order of growth, then
are of bounded mean oscillation, local Hölder continuous, or of a certain local order of growth, then  is in an appropriate oscillation class; see [9].
is in an appropriate oscillation class; see [9].
Notice that monogenic functions satisfy (5.1) just as the space of constants is a subspace of the bounded mean oscillation and Lipschitz spaces of real-valued functions.
We remark that it follows from Hölder's inequality that if  and if
and if  is of
is of  -oscillation, then
-oscillation, then  is of
is of  -oscillation.
-oscillation.
The following lemma shows that Definition 5.1 is independent of the expansion factor of the cube.
Lemma 5.2.
Suppose that  ,
,  a.e.,
a.e.,  , and
, and  If
If

then

Proof.
If  , then the implication is immediate. Assume
, then the implication is immediate. Assume  Let
Let  be a cube with
be a cube with  Dyadically subdivide
Dyadically subdivide  into a finite number of subcubes
into a finite number of subcubes  with
with  Then
Then  for all
for all  . Moreover,
. Moreover,

We use a Whitney decomposition  of
of  . The decomposition consists of closed dyadic cubes with disjoint interiors which satisfy
. The decomposition consists of closed dyadic cubes with disjoint interiors which satisfy
(a)
(b)
(c) when
when  is not empty.
is not empty.
Here  is the Euclidean distance between
is the Euclidean distance between  and the boundary of
and the boundary of  ; see [15].
; see [15].
We use the following definition. If  and
and  , then we define the
, then we define the  -inflation of
-inflation of  as
as

We now state the removability result.
Theorem 5.3.
Let  be a relatively closed subset of
be a relatively closed subset of  . Suppose that
. Suppose that  has distributional first derivatives in
has distributional first derivatives in  ,
,  is a solution to the scalar part of the
is a solution to the scalar part of the  -Dirac equation (3.13) in
-Dirac equation (3.13) in  , and
, and  is of
is of  -oscillation in
-oscillation in  . If for each compact subset
. If for each compact subset  of
of 

then  extends to a solution of the A-Dirac equation in
extends to a solution of the A-Dirac equation in  .
.
Proof.
Let  be a cube in the Whitney decomposition of
be a cube in the Whitney decomposition of  . Using the Caccioppoli estimate and the
. Using the Caccioppoli estimate and the  -oscillation condition, we have
-oscillation condition, we have

Here  . Since the problem is local (use a partition of unity), we show that (3.13) holds whenever
. Since the problem is local (use a partition of unity), we show that (3.13) holds whenever  with
with  and
and  sufficiently small. Choose
sufficiently small. Choose  and let
and let  Then
Then  is a compact subset of
is a compact subset of  . Also let
. Also let  be those cubes in the Whitney decomposition of
be those cubes in the Whitney decomposition of  which meet
which meet  Notice that each cube
Notice that each cube  lies in
lies in  Let
Let  First, since
First, since  , it follows that
, it follows that  ; see [11]. Also since
; see [11]. Also since  using (5.6) and (5.7), we obtain
using (5.6) and (5.7), we obtain

Hence 
Next let  and assume that
and assume that  . Also let
. Also let  be those cubes
be those cubes  with
with 
Consider the scalar functions

Thus each  ,
,  is Lipschitz, equal to
is Lipschitz, equal to  on
on  and as such
and as such  with compact support. Hence
with compact support. Hence

Since  is a solution in
is a solution in  ,
, 
Also we have

Now there exists a constant  such that
such that  Hence using Hölder's inequality,
Hence using Hölder's inequality,

Next using (4.4), the above is

Now for 
 is bounded above and below by a multiple of
is bounded above and below by a multiple of  and for
and for  Hence
Hence

Since  and
and  as
as  it follows that
it follows that  as
as 
Next again using Hölder's inequality,

Since  and
and  as
as  , we have that
, we have that  as
as  Hence
Hence  .
.
References
Abreu-Blaya R, Bory-Reyes J, Peña-Peña D: Jump problem and removable singularities for monogenic functions. The Journal of Geometric Analysis 2007, 17(1):1–13. 10.1007/s00039-006-0585-4
Chen Q, Jost J, Li J, Wang G: Dirac-harmonic maps. Mathematische Zeitschrift 2006, 254(2):409–432. 10.1007/s00209-006-0961-7
Chen Q, Jost J, Li J, Wang G: Regularity theorems and energy identities for Dirac-harmonic maps. Mathematische Zeitschrift 2005, 251(1):61–84. 10.1007/s00209-005-0788-7
Chen Q, Jost J, Wang G: Nonlinear Dirac equations on Riemann surfaces. Annals of Global Analysis and Geometry 2008, 33(3):253–270. 10.1007/s10455-007-9084-6
Wang C: A remark on nonlinear Dirac equations. preprint preprint
Wang C, Xu D: Regularity of Dirac-harmonic maps. International Mathematics Research Notices 2009, (20):3759–3792.
Heinonen J, Kilpeläinen T, Martio O: Nonlinear Potential Theory of Degenerate Elliptic Equations, Oxford Mathematical Monographs. Oxford University Press, New York, NY, USA; 1993:vi+363.
Nolder CA, Ryan J: -Dirac operators. Advances in Applied Clifford Algebra 2009, 19(2):391–402. 10.1007/s00006-009-0162-7
Nolder CA: Nonlinear -Dirac equations. to appear in Advances in Applied Clifford Algebra to appear in Advances in Applied Clifford Algebra
Kaufman R, Wu JM: Removable singularities for analytic or subharmonic functions. Arkiv för Matematik 1980, 18(1):107–116. 10.1007/BF02384684
Koskela P, Martio O: Removability theorems for solutions of degenerate elliptic partial differential equations. Arkiv för Matematik 1993, 31(2):339–353. 10.1007/BF02559490
Kilpeläinen T, Zhong X: Removable sets for continuous solutions of quasilinear elliptic equations. Proceedings of the American Mathematical Society 2002, 130(6):1681–1688. 10.1090/S0002-9939-01-06237-2
Meyers NG: Mean oscillation over cubes and Hölder continuity. Proceedings of the American Mathematical Society 1964, 15: 717–721.
Langmeyer N: The quasihyperbolic metric, growth, and John domains. Annales Academiæ Scientiarium Fennicæ. Mathematica 1998, 23(1):205–224.
Stein EM: Singular Integrals and Differentiability Properties of Functions, Princeton Mathematical Series, no. 30. Princeton University Press, Princeton, NJ, USA; 1970:xiv+290.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Nolder, C. A-Harmonic Equations and the Dirac Operator. J Inequal Appl 2010, 124018 (2010). https://doi.org/10.1155/2010/124018
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/124018
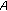 -Dirac Equation
-Dirac Equation