- Research Article
- Open access
- Published:
More About Hermite-Hadamard Inequalities, Cauchy's Means, and Superquadracity
Journal of Inequalities and Applications volume 2010, Article number: 102467 (2010)
Abstract
New results associated with Hermite-Hadamard inequalities for superquadratic functions are given. A set of Cauchy's type means is derived from these Hermite-Hadamard-type inequalities, and its log-convexity and monotonicity are proved.
1. Introduction
The following inequality:

is holding for any convex function, that is, well known in the literature as the Hermite-Hadamard inequality (see [1, page 137]). In many areas of analysis applications of Hermite-Hadamard inequality appear for different classes of functions with and without weights; see for convex functions, for example, [2, 3]. Also some useful mappings are defined connected to this inequality see in [4–6]. Here we focus on a class of functions which are superquadratic and analogs and refinements of (1.1) are applied to obtain results useful in analysis.
Now we present definitions, theorems, and results that we use in this paper.
The following definition is given in [7].
Definition A. A function  is superquadratic provided that for all
is superquadratic provided that for all  there exists a constant
there exists a constant  such that
such that

for all  . One says that
. One says that  is subquadratic if
is subquadratic if  is a superquadratic function.
is a superquadratic function.
The followings theorem is given in [8] and is used in our main results:
Theorem 1.1.
Let  be an integrable superquadratic function; then for
be an integrable superquadratic function; then for  one has
one has


Definition (see [ 9 , Definition
(see [ 9 , Definition ]). A function
]). A function  is exponentially convex if it is continuous and
is exponentially convex if it is continuous and

for all  and all choices
and all choices  and
and  such that
such that 
Proposition 1.2 (see [9, Proposition  ]).
]).
Let  . The following are equivalent:
. The following are equivalent:
(i) is exponentially convex,
is exponentially convex,
(ii) is continuous and
is continuous and

for every  and every
and every  ,
,
(iii) is continuous and
is continuous and

for every 
If  is exponentially convex function, then
is exponentially convex function, then  is a log-convex function:
is a log-convex function:

for all  .
.
Remark 1.4.
In Definition  and Proposition 1.2 it is sufficient to require measurability and finiteness almost every where in place of continuity because of the following theorem (see [10, page 105, Theorem
and Proposition 1.2 it is sufficient to require measurability and finiteness almost every where in place of continuity because of the following theorem (see [10, page 105, Theorem  .1b]
.1b] and [11]): if the function
and [11]): if the function  is measurable and finite almost everywhere and if in addition
is measurable and finite almost everywhere and if in addition

then  is continuous function.
is continuous function.
The next two sections are about mean value theorems, positive semidefiniteness, exponential convexity, log-convexity, Cauchy means, and their monotonicity, that are associated with Hermite-Hadamard inequalities for superquadratic functions.
2. Mean Value Theorems
Definition B. Let  be an integrable function; for
be an integrable function; for  one defines a linear functional
one defines a linear functional  as
as

It is clear from (1.3) Theorem 1.1 of that; if  is superquadratic function; then
is superquadratic function; then  .
.
In [7] we have the following Lemma.
Lemma 2.1.
Suppose that  is continuously differentiable and
is continuously differentiable and  . If
. If  is superadditive or
is superadditive or  is increasing, then
is increasing, then  is superquadratic.
is superquadratic.
Lemma 2.2 (see [12, Lemma  ]).
]).
Let 
 such that
such that

Consider the functions  defined as
defined as

Then  and
and  are increasing functions. If also
are increasing functions. If also  then they are superquadratic functions.
then they are superquadratic functions.
Theorem 2.3.
If  and
and  , then the following equality holds:
, then the following equality holds:

Proof.
Suppose that  is bounded, that is,
is bounded, that is,  and
and  . Using
. Using  instead of
instead of  in (1.3) we get
in (1.3) we get

Similarly, using  instead of
instead of  in (1.3) we get
in (1.3) we get

By combining the above two inequalities we get that there exists  such that (2.4) holds. Moreover if (for example)
such that (2.4) holds. Moreover if (for example)  is bounded from above we have that (2.5) is valid. Also (2.4) holds when
is bounded from above we have that (2.5) is valid. Also (2.4) holds when  is not bounded.
is not bounded.
We omit the proofs of Theorems 2.4 and 2.6 as they are similar to the proofs in [9, 13–16].
Theorem 2.4.
If  ,
,  , and
, and  , then one has
, then one has

provided the denominators are not equal to zero. If K is invertible then

is a new mean.
It is easy to check that the set of functions 


 , satisfies Lemma 2.1. Therefore if we put
, satisfies Lemma 2.1. Therefore if we put  and
and  in (2.8), we have a new mean
in (2.8), we have a new mean  defined as follows.
defined as follows.
Definition . One defines new mean
. One defines new mean  for
for  ,
,  and
and  ,
,  , as follows:
, as follows:

When  goes to 2, we have
goes to 2, we have

where

When  goes to 2 we have
goes to 2 we have

where  is defined above and
is defined above and

In  when
when  goes to
goes to  , we have
, we have

where

If we put  and
and  in (2.8), then by the substitution,
in (2.8), then by the substitution,  , we have a new mean defined as
, we have a new mean defined as
Definition . Let
. Let  and
and  ,
,  one defines Cauchy mean
one defines Cauchy mean  as
as

where denotes
denotes  and
and  denotes
denotes  . In limiting case when
. In limiting case when  goes to 2s
goes to 2s  is equal to
is equal to

where denotes
denotes  and
and  denotes
denotes  . When
. When  goes to
goes to  we have,
we have,

where

When  goes to
goes to  in
in  , we have
, we have

where

Definition C. Let  be an integrable function, for
be an integrable function, for  One defines a linear functional
One defines a linear functional  as
as

It is clear from (1.4) Theorem 1.1 of that if  is superquadratic function, then
is superquadratic function, then  .
.
Theorem 2.5.
If  and
and  , then the following equality holds,
, then the following equality holds,

Proof.
Suppose that  is bounded, that is,
is bounded, that is,  and
and  . Using
. Using  from Lemma 2.2 instead of
from Lemma 2.2 instead of  in (1.4), we get
in (1.4), we get

Similarly, using  from Lemma 2.2 instead of
from Lemma 2.2 instead of  in (1.4) we get
in (1.4) we get

By combining the above two inequalities we get that there exist  such that (2.23) holds. Moreover if (for example)
such that (2.23) holds. Moreover if (for example)  is bounded from above we have that (2.24) is valid. Also (2.23) holds when
is bounded from above we have that (2.24) is valid. Also (2.23) holds when  is not bounded.
is not bounded.
Theorem 2.6.
If  ,
,  and
and  then, one has
then, one has

provided the denominators are not equal to zero. If T is invertible, then

is a new mean.
If we put  and
and  in (2.27) we have new mean
in (2.27) we have new mean  defined as follows.
defined as follows.
Definition . We define
. We define  for
for  ,
,  ,
,  as follows:
as follows:

where  denotes
denotes  and
and  denotes
denotes  . In the limiting case we have
. In the limiting case we have  which is equal to
which is equal to

where  denotes
denotes 

where

In  when
when  goes to
goes to  , we have
, we have

where

If we put  and
and  in (2.27), then by the substitution
in (2.27), then by the substitution  we have new mean
we have new mean  defined as follows.
defined as follows.
Definition . Let
. Let  , and
, and  ,
,  , one defines Cauchy mean
, one defines Cauchy mean  as follows:
as follows:

where denotes
denotes  and
and denotes
denotes  . In limiting case we have
. In limiting case we have  which is equal to
which is equal to

where

When  approaches to
approaches to  ,
,

where

where

3. Positive Semidefiniteness, Exponential Convexity, and Log-Convexity
Lemma 3.1 (see [12, Lemma  ]).
]).
Consider the function  for
for  defined as
defined as

Then, with the convention  ,
,  is superquadratic.
is superquadratic.
Theorem 3.2.
For  defined in (2.1) one has the following.
defined in (2.1) one has the following.
(a)The matrix  ,
,  , is a positive semidefinite matrix, that is,
, is a positive semidefinite matrix, that is,

(b)One has

that is,  is log-convex in the Jensen sense.
is log-convex in the Jensen sense.
(c)The function  is exponentially convex.
is exponentially convex.
(d) is log-convex, that is, for
is log-convex, that is, for  where
where  one has
one has

Proof.
-
(a)
Define the function
 , where
, where  Then,
Then,  (3.5)
(3.5)
and  This implies that
This implies that  is superquadratic, so using this
is superquadratic, so using this  in the place of
in the place of  in (2.1) we have
in (2.1) we have

From this we have that the matrix  is positive semidefinite.
is positive semidefinite.
-
(b)
It is a simple consequence of
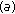 for
for 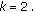
-
(c)
Since we have
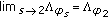 , so
, so  is continuous for all
is continuous for all  ; then by (3.6) and Proposition 1.2 we have that
; then by (3.6) and Proposition 1.2 we have that 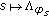 is exponentially convex.
is exponentially convex. -
(d)
As
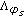 is continuous then we have that
is continuous then we have that 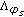 is log-convex and we get (3.4).
is log-convex and we get (3.4).
Corollary 3.3.
One has the following
(i)For  ,
,

(ii)For  ,
,

(iii)For  ,
,

(iv)For  ,
,

Proof.
By applying Theorem 3.2(b) with  and
and  respectively, we get the result.
respectively, we get the result.
Similar to Theorem 3.2 we get the following.
Theorem 3.4.
For  defined in (2.22) one has the following.
defined in (2.22) one has the following.
(a)The matrix  ,
,  , is a positive-semidefinite matrix, that is,
, is a positive-semidefinite matrix, that is,

(b)One has

that is,  is log-convex in the Jensen sense.
is log-convex in the Jensen sense.
(c)The function  is exponentially convex.
is exponentially convex.
(d) is log-convex, that is, for
is log-convex, that is, for  where
where  one has
one has

Proof.
The proof is the same as the proof of Theorem 3.2.
In the next results we use the continuity of  and
and  .
.
When log f is convex we see that (also see [13])
Lemma 3.5.
Let  be log-convex function, and if
be log-convex function, and if  , then the following inequality is valid,
, then the following inequality is valid,

Theorem 3.6.
For  such that
such that  and
and  , one has for
, one has for  as in Definition
as in Definition 

Proof.
According to Theorem 3.2,  defined above is log-convex; so Lemma 3.5 implies that for
defined above is log-convex; so Lemma 3.5 implies that for  such that
such that  and
and  we have
we have

From the continuity of  we get our result for
we get our result for  ,
,  , and for
, and for  we can consider limiting case.
we can consider limiting case.
Theorem 3.7.
For  such that
such that  and
and  , one has for
, one has for  as in Definition
as in Definition 

Proof.
As  defined above is log-convex, Lemma 3.5 implies that for
defined above is log-convex, Lemma 3.5 implies that for  such that
such that  and
and  we have
we have

By substituting 



 , and
, and  , such that
, such that  ,
,  ,
,  we get the result, and for
we get the result, and for  ,
, we can consider the limiting case.
we can consider the limiting case.
Theorem 3.8.
For  such that
such that  and
and  , one has
, one has

Proof.
According to Theorem 3.4,  defined above is log-convex; so Lemma 3.5 implies that for
defined above is log-convex; so Lemma 3.5 implies that for  such that
such that  and
and  we have
we have

From the continuity of  we get our result for
we get our result for  ,
,  ; and for
; and for  we can consider limiting case.
we can consider limiting case.
Theorem 3.9.
For  such that
such that  and
and  , one has
, one has

Proof.
As  defined above is log-convex, Lemma 3.5 implies that for
defined above is log-convex, Lemma 3.5 implies that for  such that
such that  and
and  we have
we have

By substituting 



 , and
, and  , such that
, such that  ,
,  ,
,  we get the result, and for
we get the result, and for  ,
, we can consider the limiting case.
we can consider the limiting case.
References
Pečarić JE, Proschan F, Tong YL: Convex Functions, Partial Orderings, and Statistical Applications, Mathematics in Science and Engineering. Volume 187. Academic Press, Boston, Mass, USA; 1992:xiv+467.
Dragomir SS: On Hadamard's inequalities for convex functions. Mathematica Balkanica 1992, 6(3):215–222.
Dragomir SS, McAndrew A: Refinements of the Hermite-Hadamard inequality for convex functions. Journal of Inequalities in Pure and Applied Mathematics 2005., 6(5, article 140):
Banić S: Mappings connected with Hermite-Hadamard inequalities for superquadratic functions. Journal of Mathematical Inequalities 2009, 3(4):577–589.
Dragomir SS: A mapping in connection to Hadamard's inequalities. Akademie der Wissenschaften. Mathematisch-Naturwissenschaftliche Klasse 1991, 128: 17–20.
Dragomir SS: Two mappings in connection to Hadamard's inequalities. Journal of Mathematical Analysis and Applications 1992, 167(1):49–56. 10.1016/0022-247X(92)90233-4
Abramovich S, Jameson G, Sinnamon G: Refining Jensen's inequality. Bulletin Mathématique de la Société des Sciences Mathématiques de Roumanie 2004, 47(1–2):3–14.
Banić S, Varošanec S: Functional inequalities for superquadratic functions. International Journal of Pure and Applied Mathematics 2008, 43(4):537–549.
Anwar M, Jakšetić J, Pečarić J, Atiq Ur Rehman : Exponential convexity, positive semi-definite matrices and fundamental inequalities. accepted in Journal of Mathematical Inequalities accepted in Journal of Mathematical Inequalities
Hirschman II, Widder DV: The Convolution Transform. Princeton University Press, Princeton, NJ, USA; 1955:x+268.
Sierpinski W: A family of the Cauchy type mean-value theorems. Fundamenta Mathematicae 1920, 1: 125–129.
Abramovich S, Farid G, Pečarić J: More About Jensen's Inequality and Cauchy's Means for Superquadratic Functions. submitted submitted
Anwar M, Latif N, Pečarić J: Cauchy means of the Popoviciu type. Journal of Inequalities and Applications 2009, 2009:-16.
Anwar M, Pečarić J: Cauchy's means of Levinson type. Journal of Inequalities in Pure and Applied Mathematics 2008, 9(4, article 120):8.
Anwar M, Pečarić J: New means of Cauchy's type. Journal of Inequalities and Applications 2008, 2008:-10.
Pečarić JE, Perić I, Srivastava HM: A family of the Cauchy type mean-value theorems. Journal of Mathematical Analysis and Applications 2005, 306(2):730–739. 10.1016/j.jmaa.2004.10.018
Acknowledgment
This research was partially funded by Higher Education Commission, Pakistan. The research of the third author was supported by the Croatian Ministry of Science, Education and Sports under the Research grant no. 117-1170889-0888.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Abramovich, S., Farid, G. & Pečarić, J. More About Hermite-Hadamard Inequalities, Cauchy's Means, and Superquadracity. J Inequal Appl 2010, 102467 (2010). https://doi.org/10.1155/2010/102467
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/102467
 , where
, where  Then,
Then, 
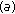 for
for 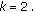
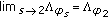 , so
, so  is continuous for all
is continuous for all  ; then by (3.6) and Proposition 1.2 we have that
; then by (3.6) and Proposition 1.2 we have that 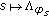 is exponentially convex.
is exponentially convex.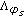 is continuous then we have that
is continuous then we have that 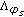 is log-convex and we get (3.4).
is log-convex and we get (3.4).