- Research Article
- Open access
- Published:
On Interpolation Functions of the Generalized Twisted 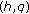 -Euler Polynomials
-Euler Polynomials
Journal of Inequalities and Applications volume 2009, Article number: 946569 (2009)
Abstract
The aim of this paper is to construct  -adic twisted two-variable Euler-(
-adic twisted two-variable Euler-( ,
, )-
)- -functions, which interpolate generalized twisted (
-functions, which interpolate generalized twisted ( ,
, )-Euler polynomials at negative integers. In this paper, we treat twisted (
)-Euler polynomials at negative integers. In this paper, we treat twisted ( ,
, )-Euler numbers and polynomials associated with
)-Euler numbers and polynomials associated with  -adic invariant integral on
-adic invariant integral on  . We will construct two-variable twisted (
. We will construct two-variable twisted ( ,
, )-Euler-zeta function and two-variable (
)-Euler-zeta function and two-variable ( ,
, )-
)- -function in Complex
-function in Complex  -plane.
-plane.
1. Introduction
Tsumura and Young treated the interpolation functions of the Bernoulli and Euler polynomials in [1, 2]. Kim and Simsek studied on  -adic interpolation functions of these numbers and polynomials [3–48]. In [49], Carlitz originally constructed
-adic interpolation functions of these numbers and polynomials [3–48]. In [49], Carlitz originally constructed  -Bernoulli numbers and polynomials. Many authors studied these numbers and polynomials [4, 28, 38, 41, 50]. After that, twisted
-Bernoulli numbers and polynomials. Many authors studied these numbers and polynomials [4, 28, 38, 41, 50]. After that, twisted  -Bernoulli and Euler numbers(polynomials) were studied by several authors [1–32, 32–65]. In [62], Whashington constructed one-variable
-Bernoulli and Euler numbers(polynomials) were studied by several authors [1–32, 32–65]. In [62], Whashington constructed one-variable  -adic-
-adic- -function which interpolates generalized classical Bernoulli numbers at negative integers. Fox introduced the two-variable
-function which interpolates generalized classical Bernoulli numbers at negative integers. Fox introduced the two-variable  -adi
-adi  -functions [53]. Young defined
-functions [53]. Young defined  -adic integral representation for the two-variable
-adic integral representation for the two-variable  -adic
-adic  -functions [64]. Furthermore, Kim constructed the two-variable
-functions [64]. Furthermore, Kim constructed the two-variable  -adic
-adic  -
- -function, which is interpolation function of the generalized
-function, which is interpolation function of the generalized  -Bernoulli polynomials [8]. This function is the
-Bernoulli polynomials [8]. This function is the  -extension of the two-variable
-extension of the two-variable  -adic
-adic  -function. Kim constructed
-function. Kim constructed  -extension of the generalized formula for two-variable of Diamond and Ferrero and Greenberg formula for two-variable
-extension of the generalized formula for two-variable of Diamond and Ferrero and Greenberg formula for two-variable  -adic
-adic  -function in the terms of the
-function in the terms of the  -adic gamma and log-gamma functions [8]. Kim and Rim introduced twisted
-adic gamma and log-gamma functions [8]. Kim and Rim introduced twisted  -Euler numbers and polynomials associated with basic twisted
-Euler numbers and polynomials associated with basic twisted  -
- -functions [28]. Also, Jang et al. investigated the
-functions [28]. Also, Jang et al. investigated the  -adic analogue twisted
-adic analogue twisted  -
- -function, which interpolates generalized twisted
-function, which interpolates generalized twisted  -Euler numbers
-Euler numbers  attached to Dirichlet's character
attached to Dirichlet's character  [55]. Kim et al. have studied two-variable
[55]. Kim et al. have studied two-variable  -adic
-adic  -functions, which interpolate the generalized Bernoulli polynomials at negative integers. In this paper, we will construct two-variale
-functions, which interpolate the generalized Bernoulli polynomials at negative integers. In this paper, we will construct two-variale  -adic twisted Euler
-adic twisted Euler  -
- -functions. This functions interpolation functions of the generalized twisted
-functions. This functions interpolation functions of the generalized twisted  -Euler polynomials.
-Euler polynomials.
Let  be a fixed odd prime number. Throughout this paper
be a fixed odd prime number. Throughout this paper  and
and  will respectively denote the ring of rational integers, the ring of
will respectively denote the ring of rational integers, the ring of  -adic rational integers, the field of
-adic rational integers, the field of  -adic rational numbers and the completion of the algebraic closure of
-adic rational numbers and the completion of the algebraic closure of  . Let
. Let  be the normalized exponential valuation of
be the normalized exponential valuation of  such that
such that  . If
. If  , then
, then  . If
. If  , we normally assume
, we normally assume  , so that
, so that  for
for  . Throughout this paper we use the following notations (cf. [1–32, 32–48, 50, 51, 54–65]):
. Throughout this paper we use the following notations (cf. [1–32, 32–48, 50, 51, 54–65]):

Hence,  , for any
, for any  with
with  in the present
in the present  -adic case.
-adic case.
For  a fixed positive integer with
a fixed positive integer with  , set
, set

where  satisfies the condition
satisfies the condition  . The distribution is defined by
. The distribution is defined by

We say that  is uniformly differential function at a point
is uniformly differential function at a point  , and we write
, and we write  , if the difference quotients,
, if the difference quotients,  have a limit
have a limit  as
as  .
.
For  , the
, the  -adic invariant
-adic invariant  -integral on
-integral on  is defined as [4, 18]
is defined as [4, 18]

The fermionic  -adic
-adic  -measures on
-measures on  is defined as (cf. [14–16, 18, 22, 28])
is defined as (cf. [14–16, 18, 22, 28])

for  . For
. For  , the ferminoic
, the ferminoic  -adic invariant
-adic invariant  -integral on
-integral on  is defined as
is defined as

which has a sense as we see readily that the limit is convergent. For  , we note that (cf. [14, 16, 18, 22, 28])
, we note that (cf. [14, 16, 18, 22, 28])

From the fermionic invariant integral on  , we derive the following integral equation (cf. [14, 35]):
, we derive the following integral equation (cf. [14, 35]):

where  .
.
2. Twisted  -Euler Numbers and Polynomials
-Euler Numbers and Polynomials
In this section, we will treat some properties of twisted  -Euler numbers and polynomials associated with
-Euler numbers and polynomials associated with  -adic invariant integral on
-adic invariant integral on  . From now on, we take
. From now on, we take  and
and  with
with  . Let
. Let  be the space of primitive
be the space of primitive  th root of unity,
th root of unity,

Then, we denote

Hence  is a
is a  -adic locally constant space. For
-adic locally constant space. For  , we denote by
, we denote by  defined by
defined by  , the locally constant function. If we take
, the locally constant function. If we take  , then we have (cf. [35])
, then we have (cf. [35])

By induction in (1.8), Kim constructed the following useful identity (cf. [14, 28]):

where  . From (2.4), if
. From (2.4), if  is odd, then we have
is odd, then we have

If we replace  by
by  into (2.5), we obtain
into (2.5), we obtain

Let  . Let
. Let  be a Dirichlet's character of conductor
be a Dirichlet's character of conductor  , which
, which  is any multiple of
is any multiple of  with
with  . By substituting
. By substituting  into (2.6), we have
into (2.6), we have

Remark 2.1.
In complex case, the generating function of the Euler numbers  is given by (cf. [28])
is given by (cf. [28])

By using Taylor series of  , then we can define the generalized twisted Euler numbers
, then we can define the generalized twisted Euler numbers  attached to
attached to  as follows (cf. [55]):
as follows (cf. [55]):

In [8],  -Euler numbers were defined by
-Euler numbers were defined by

where  and
and  . In particular, if we take
. In particular, if we take  , then
, then  . These numbers are called
. These numbers are called  -Euler numbers.
-Euler numbers.
By using iterative method of  -adic invariant integral on
-adic invariant integral on  in the sense of fermionic, we define twisted
in the sense of fermionic, we define twisted  -Euler numbers as follows (cf. [55]):
-Euler numbers as follows (cf. [55]):

For  and
and  , we have that (cf. [55])
, we have that (cf. [55])


where  with
with  .
.
Let  be the generating function of
be the generating function of  in complex plane as follows (cf. [55]):
in complex plane as follows (cf. [55]):

Let  be the Dirichlet's character with conductor
be the Dirichlet's character with conductor  with
with  . Then the generalized twisted
. Then the generalized twisted  -Euler polynomials attached to
-Euler polynomials attached to  is given by as follows:
is given by as follows:
For  ,
,

where  is any multiple of
is any multiple of  with
with  and
and  .
.
Then the distribution relation of the generalized twisted  -Euler polynomials is given by as follows (cf. [14]):
-Euler polynomials is given by as follows (cf. [14]):

3. Two-Variable Twisted 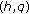 -Euler-Zeta Function and
-Euler-Zeta Function and 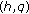 -
-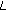 -Function
-Function
In this section, we will construct two-variable twisted  -Euler-zeta function and two-variable
-Euler-zeta function and two-variable  -
- -function in Complex
-function in Complex  -plane. We assume
-plane. We assume  with
with  .
.
Firstly, we consider twisted  -Euler numbers and polynomials in
-Euler numbers and polynomials in  as follows (cf. [55]):
as follows (cf. [55]):

where  and
and  is
is  th root of unity. In particular, if we take
th root of unity. In particular, if we take  , then we have
, then we have  . These numbers are called twisted Euler numbers. By using derivative operator, we have
. These numbers are called twisted Euler numbers. By using derivative operator, we have  .
.
From (3.1), we can define Hurwitz-type twisted  -Euler-zeta function as follows (cf. [55]):
-Euler-zeta function as follows (cf. [55]):

where  and
and  . Note that if
. Note that if  in (3.2), then we see that the twisted
in (3.2), then we see that the twisted  -Euler-zeta function is defined by (cf. [28, 55])
-Euler-zeta function is defined by (cf. [28, 55])

For  , we know (cf. [28])
, we know (cf. [28])

From now on, we will define the two-variable  -
- -functions
-functions  which interpolates the generalized
which interpolates the generalized  -Euler polynomials.
-Euler polynomials.
Definition 3.1.
Let  be the Dirichlet's character with conductor
be the Dirichlet's character with conductor  with
with  . For
. For  and
and  , we define
, we define

By substituting  and
and  into (3.5), then using (3.2), we have
into (3.5), then using (3.2), we have

Thus, we see the function  which interpolates the generalized
which interpolates the generalized  -Euler polynomials as follows.
-Euler polynomials as follows.
Theorem 3.2.
For  , let
, let  be the Dirichlet's character with conductor
be the Dirichlet's character with conductor  with
with  . Then one has
. Then one has

By substituting  with
with  , into (3.7), we obtain
, into (3.7), we obtain

where  .
.
Thus, we have the following theorem.
Theorem 3.3.
For  , let
, let  be the Dirichlet's character with conductor
be the Dirichlet's character with conductor  with
with  . Then one has
. Then one has

Remark 3.4.
If we take  in (3.5), then we have (cf. [28, 55])
in (3.5), then we have (cf. [28, 55])

From (3.9) and (3.10), we have the following corollary.
Corollary 3.5.
Let  be the Dirichlet's character with conductor
be the Dirichlet's character with conductor  with
with  . Then one has
. Then one has

Secondly, we will define two-variable twisted Euler  -
- -function as follows.
-function as follows.
Definition 3.6.
Let  be the Dirichlet's character with conductor
be the Dirichlet's character with conductor  with
with  . For
. For  and
and  with
with  , we define
, we define

We consider the well-known identity (cf. [44, 65])

By using (3.12), we define two-variable twisted Euler  -
- -function as follows:
-function as follows:

We will investigate the relations between  and
and  as follows.
as follows.
Substituting  with
with  into (3.12), we have
into (3.12), we have

Thus we obtain the following theorem.
Theorem 3.7.
For  with
with  , let
, let  be the Dirichlet character with conductor
be the Dirichlet character with conductor  with
with  and
and  with
with  . Then one has
. Then one has

By substituting  with
with  into (3.16) and using (3.4), we can obtain
into (3.16) and using (3.4), we can obtain

Thus, we see that the function  interpolates generalized
interpolates generalized  -Euler polynomials attached to
-Euler polynomials attached to  at negative integer values of
at negative integer values of  as followings.
as followings.
Theorem 3.8.
For  , let
, let  be the Dirichlet's character with odd conductor
be the Dirichlet's character with odd conductor  . Then one has
. Then one has

Note that if we take  , then Theorem 3.8 reduces to Theorem 3.3.
, then Theorem 3.8 reduces to Theorem 3.3.
Let  and
and  be integers with
be integers with  and
and  . For
. For  , we define partial
, we define partial  -Hurwitz type zeta function
-Hurwitz type zeta function  as follows:
as follows:

By substituting  , we have
, we have

By substituting (3.2), for  , we get
, we get

Equation (3.20) means that the function  interpolates
interpolates  polynomials at negative integers.
polynomials at negative integers.
From (3.16) and (3.20), we have the following theorem.
Theorem 3.9.
For  with
with  , let
, let  be the Dirichlet's character with conductor
be the Dirichlet's character with conductor  with
with  and
and  ,
,  is any multiple of
is any multiple of  . Then one has
. Then one has

Remark 3.10.
If we take  in (3.22), then we have
in (3.22), then we have

From (2.12), if we take  , then we have the following corollary.
, then we have the following corollary.
Corollary 3.11.
For  with
with  , let
, let  be the Dirichlet's character with conductor
be the Dirichlet's character with conductor  with
with  and
and  ,
,  is any multiple of
is any multiple of  . Then one has
. Then one has

4. 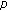 -Adic Twisted Two-Variable Euler
-Adic Twisted Two-Variable Euler  -L-Functions
-L-Functions
In [62], Washington constructed one-variable  -adic-
-adic- -function which interpolates generalized classical Bernoulli numbers negative integers. Kim [22] investigated the
-function which interpolates generalized classical Bernoulli numbers negative integers. Kim [22] investigated the  -adic analogues of two-variables Euler
-adic analogues of two-variables Euler  -
- -function. In this section, we will construct
-function. In this section, we will construct  -adic twisted two-variable Euler-
-adic twisted two-variable Euler- -
- -functions, which interpolate generalized twisted
-functions, which interpolate generalized twisted  -Euler polynomials at negative integers. Our notations and methods are essentially due to Kim and Washington (cf. [22, 62]).
-Euler polynomials at negative integers. Our notations and methods are essentially due to Kim and Washington (cf. [22, 62]).
We assume that  with
with  , so that
, so that  . Let
. Let  be an odd prime number. Let
be an odd prime number. Let  denote the Teichmüller character having conductor
denote the Teichmüller character having conductor  . For an arbitrary character
. For an arbitrary character  , we define
, we define  , where
, where  , in the sense of the product of characters. Let
, in the sense of the product of characters. Let  . Then
. Then  . Hence we see that
. Hence we see that

where  with
with  .
.
We denote the subset  of
of  by (cf. [62])
by (cf. [62])

Let

be a sequence of power series, each of which converges in a fixed subset  such that
such that
(1) as
as  and
and
(2)for each  and
and  , there exists
, there exists  such that
such that

Then  for all
for all  (cf. [2, 22, 50, 51, 60, 62]).
(cf. [2, 22, 50, 51, 60, 62]).
Let  be the Dirichlet's character with conductor
be the Dirichlet's character with conductor  with
with  and let
and let  be a positive multiple of
be a positive multiple of  and
and  .
.
Now we set

Then  is analytic for
is analytic for  with
with  , when
, when  . For
. For  with
with  , we have
, we have

is analytic for  . It readily follows that
. It readily follows that

is analytic for  with
with  when
when  . Thus we see that
. Thus we see that

Let  and fixed
and fixed  with
with  . Then we have that
. Then we have that

If  , then
, then  , so
, so  is a multiple of
is a multiple of  . Therefore, we have
. Therefore, we have

Then we note that

The difference of these equations yields

Using distribution for  -Euler polynomials, we easily see that
-Euler polynomials, we easily see that

Since  , for
, for  , and
, and  , with
, with  , we have
, we have

From (4.5)–(4.14), we can derive that

Therefore we obtain the following theorem.
Theorem 4.1.
Let  be a positive integral multiple of
be a positive integral multiple of  and
and  with
with  , and let
, and let

Then  is analytic for
is analytic for  , provides
, provides  when
when  . Furthermore, for each
. Furthermore, for each  , we have
, we have

Thus we note that  for all
for all  , where
, where  is twisted
is twisted  -adic Euler
-adic Euler  -
- -function, (cf. [15, 22]).
-function, (cf. [15, 22]).
We now generalized to two-variable  -adic Euler
-adic Euler  -
- -function,
-function,  which is first defined by the interpolation function
which is first defined by the interpolation function

for  .
.
From (4.18), we have that

By using the definition of  , we can express
, we can express  for all
for all  and
and  with
with  as follows:
as follows:

We know that  is analytic for
is analytic for  , when
, when  . The value of
. The value of  is the coefficients of
is the coefficients of  in the expansion of
in the expansion of  at
at  . Using the Taylor expansion at
. Using the Taylor expansion at  , we see that
, we see that

The  -adic logarithmic function,
-adic logarithmic function,  , is the unique function
, is the unique function  that satisfies
that satisfies

By employing these expansion and some algebraic manipulations, we evaluate the derivative  . It follows from the definition of
. It follows from the definition of  that
that

Thus, we have

Since  is a root of unity for
is a root of unity for  , we have
, we have

Thus we have the following theorem.
Theorem 4.2.

Let  be a primitive Dirichlet's character with odd conductor
be a primitive Dirichlet's character with odd conductor  and let
and let  be a odd positive integral multiple of
be a odd positive integral multiple of  and
and  . Then for any
. Then for any  with
with  , one has
, one has

References
Tsumura H: On a
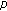 -adic interpolation of the generalized Euler numbers and its applications. Tokyo Journal of Mathematics 1987,10(2):281–293. 10.3836/tjm/1270134514
-adic interpolation of the generalized Euler numbers and its applications. Tokyo Journal of Mathematics 1987,10(2):281–293. 10.3836/tjm/1270134514Young PT: Congruences for Bernoulli, Euler, and Stirling numbers. Journal of Number Theory 1999,78(2):204–227. 10.1006/jnth.1999.2401
Kim T: On a
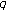 -analogue of the
-analogue of the  -adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320–329. 10.1006/jnth.1999.2373
-adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320–329. 10.1006/jnth.1999.2373Kim T:
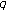 -Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288–299.
-Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288–299.Kim T: On Euler-Barnes multiple zeta functions. Russian Journal of Mathematical Physics 2003,10(3):261–267.
Kim T:
 -Riemann zeta function. International Journal of Mathematics and Mathematical Sciences 2004,2004(12):599–605. 10.1155/S0161171204307180
-Riemann zeta function. International Journal of Mathematics and Mathematical Sciences 2004,2004(12):599–605. 10.1155/S0161171204307180Kim T: Analytic continuation of multiple
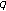 -zeta functions and their values at negative integers. Russian Journal of Mathematical Physics 2004,11(1):71–76.
-zeta functions and their values at negative integers. Russian Journal of Mathematical Physics 2004,11(1):71–76.Kim T: Power series and asymptotic series associated with the
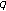 -analog of the two-variable
-analog of the two-variable 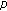 -adic
-adic 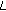 -function. Russian Journal of Mathematical Physics 2005,12(2):186–196.
-function. Russian Journal of Mathematical Physics 2005,12(2):186–196.Kim T:
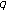 -generalized Euler numbers and polynomials. Russian Journal of Mathematical Physics 2006,13(3):293–298. 10.1134/S1061920806030058
-generalized Euler numbers and polynomials. Russian Journal of Mathematical Physics 2006,13(3):293–298. 10.1134/S1061920806030058Kim T: A new approach to
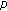 -adic
-adic  -
-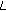 -functions. Advanced Studies in Contemporary Mathematics 2006,12(1):61–72.
-functions. Advanced Studies in Contemporary Mathematics 2006,12(1):61–72.Kim T: A note on
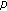 -adic invariant integral in the rings of
-adic invariant integral in the rings of 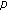 -adic integers. Advanced Studies in Contemporary Mathematics 2006,13(1):95–99.
-adic integers. Advanced Studies in Contemporary Mathematics 2006,13(1):95–99.Kim T: Multiple
 -adic
-adic 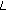 -function. Russian Journal of Mathematical Physics 2006,13(2):151–157. 10.1134/S1061920806020038
-function. Russian Journal of Mathematical Physics 2006,13(2):151–157. 10.1134/S1061920806020038Kim T:
 -extension of the Euler formula and trigonometric functions. Russian Journal of Mathematical Physics 2007,14(3):275–278. 10.1134/S1061920807030041
-extension of the Euler formula and trigonometric functions. Russian Journal of Mathematical Physics 2007,14(3):275–278. 10.1134/S1061920807030041Kim T: On the analogs of Euler numbers and polynomials associated with
 -adic
-adic  -integral on
-integral on  at
at 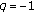 . Journal of Mathematical Analysis and Applications 2007,331(2):779–792. 10.1016/j.jmaa.2006.09.027
. Journal of Mathematical Analysis and Applications 2007,331(2):779–792. 10.1016/j.jmaa.2006.09.027Kim T: On
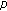 -adic
-adic 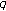 -
- -functions and sums of powers. Journal of Mathematical Analysis and Applications 2007,329(2):1472–1481. 10.1016/j.jmaa.2006.07.071
-functions and sums of powers. Journal of Mathematical Analysis and Applications 2007,329(2):1472–1481. 10.1016/j.jmaa.2006.07.071Kim T: On the
 -extension of Euler and Genocchi numbers. Journal of Mathematical Analysis and Applications 2007,326(2):1458–1465. 10.1016/j.jmaa.2006.03.037
-extension of Euler and Genocchi numbers. Journal of Mathematical Analysis and Applications 2007,326(2):1458–1465. 10.1016/j.jmaa.2006.03.037Kim T: A note on
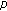 -adic
-adic 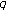 -integral on
-integral on 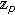 associated with
associated with 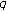 -Euler numbers. Advanced Studies in Contemporary Mathematics 2007,15(2):133–137.
-Euler numbers. Advanced Studies in Contemporary Mathematics 2007,15(2):133–137.Kim T:
 -Euler numbers and polynomials associated with
-Euler numbers and polynomials associated with 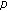 -adic
-adic  -integrals. Journal of Nonlinear Mathematical Physics 2007,14(1):15–27. 10.2991/jnmp.2007.14.1.3
-integrals. Journal of Nonlinear Mathematical Physics 2007,14(1):15–27. 10.2991/jnmp.2007.14.1.3Kim T: Euler numbers and polynomials associated with zeta functions. Abstract and Applied Analysis 2008, 2008:-11.
Kim T:
 -Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51–57.
-Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51–57.Kim T: Note on the Euler numbers and polynomials. Advanced Studies in Contemporary Mathematics 2008,17(2):109–115.
Kim T: On
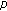 -adic interpolating function for
-adic interpolating function for 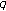 -Euler numbers and its derivatives. Journal of Mathematical Analysis and Applications 2008,339(1):598–608. 10.1016/j.jmaa.2007.07.027
-Euler numbers and its derivatives. Journal of Mathematical Analysis and Applications 2008,339(1):598–608. 10.1016/j.jmaa.2007.07.027Kim T: A note on
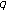 -Euler numbers and polyomials. Advanced Studies in Contemporary Mathematics 2008,16(2):161–170.
-Euler numbers and polyomials. Advanced Studies in Contemporary Mathematics 2008,16(2):161–170.Kim T: The modified
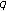 -Euler numbers and polynomials. Advanced Studies in Contemporary Mathematics 2008,16(2):161–170.
-Euler numbers and polynomials. Advanced Studies in Contemporary Mathematics 2008,16(2):161–170.Kim T: On a
 -adic interpolation function for the
-adic interpolation function for the 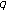 -adic interpolation function for the -extension of the generalized Bernoulli polynomials and its derivative. Discrete Mathematics 2009,309(6):1593–1602. 10.1016/j.disc.2008.03.001
-adic interpolation function for the -extension of the generalized Bernoulli polynomials and its derivative. Discrete Mathematics 2009,309(6):1593–1602. 10.1016/j.disc.2008.03.001Kim T: Note on the Euler -zeta functions. Journal of Number Theory. In press Journal of Number Theory. In press
Kim T, Choi JY, Sug JY: Extended
 -Euler numbers and polynomials associated with fermionic
-Euler numbers and polynomials associated with fermionic 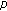 -adic
-adic  -integral on
-integral on  .Russian Journal of Mathematical Physics 2007,14(2):160–163. 10.1134/S1061920807020045
.Russian Journal of Mathematical Physics 2007,14(2):160–163. 10.1134/S1061920807020045Kim T, Rim S-H: On the twisted
 -Euler numbers and polynomials associated with basic
-Euler numbers and polynomials associated with basic  -
- -functions. Journal of Mathematical Analysis and Applications 2007,336(1):738–744. 10.1016/j.jmaa.2007.03.035
-functions. Journal of Mathematical Analysis and Applications 2007,336(1):738–744. 10.1016/j.jmaa.2007.03.035Ozden H, Cangul IN, Simsek Y: Remarks on sum of products of (
 ,
, )-twisted Euler polynomials and numbers. Journal of Inequalities and Applications 2008, 2008:-8.
)-twisted Euler polynomials and numbers. Journal of Inequalities and Applications 2008, 2008:-8.Ozden H, Simsek Y, Cangul IN: Euler polynomials associated with
 -adic
-adic  -Euler measure. General Mathematics 2007,15(2):24–37.
-Euler measure. General Mathematics 2007,15(2):24–37.Ozden H, Simsek Y: A new extension of
 -Euler numbers and polynomials related to their interpolation functions. Applied Mathematics Letters 2008,21(9):934–939. 10.1016/j.aml.2007.10.005
-Euler numbers and polynomials related to their interpolation functions. Applied Mathematics Letters 2008,21(9):934–939. 10.1016/j.aml.2007.10.005Cangul IN, Ozden H, Simsek Y: Generating functions of the (
 ,
,  ) extension of twisted Euler polynomials and numbers. Acta Mathematica Hungarica 2008,120(3):281–299. 10.1007/s10474-008-7139-1
) extension of twisted Euler polynomials and numbers. Acta Mathematica Hungarica 2008,120(3):281–299. 10.1007/s10474-008-7139-1Ozden H, Cangul IN, Simsek Y: Multivariate interpolation functions of higher-order
 -Euler numbers and their applications. Abstract and Applied Analysis 2008, 2008:-16.
-Euler numbers and their applications. Abstract and Applied Analysis 2008, 2008:-16.Simsek Y, Yurekli O, Kurt V: On interpolation functions of the twisted generalized Frobenius-Euler numbers. Advanced Studies in Contemporary Mathematics 2007,15(2):187–194.
Rim S-H, Kim T: A note on
 -Euler numbers associated with the basic
-Euler numbers associated with the basic 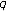 -zeta function. Applied Mathematics Letters 2007,20(4):366–369. 10.1016/j.aml.2006.04.019
-zeta function. Applied Mathematics Letters 2007,20(4):366–369. 10.1016/j.aml.2006.04.019Simsek Y: Theorems on twisted
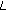 -function and twisted Bernoulli numbers. Advanced Studies in Contemporary Mathematics 2005,11(2):205–218.
-function and twisted Bernoulli numbers. Advanced Studies in Contemporary Mathematics 2005,11(2):205–218.Simsek Y:
 -analogue of twisted
-analogue of twisted  -series and
-series and 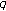 -twisted Euler numbers. Journal of Number Theory 2005,110(2):267–278. 10.1016/j.jnt.2004.07.003
-twisted Euler numbers. Journal of Number Theory 2005,110(2):267–278. 10.1016/j.jnt.2004.07.003Simsek Y: On
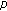 -adic twisted
-adic twisted  -
-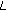 -functions related to generalized twisted Bernoulli numbers. Russian Journal of Mathematical Physics 2006,13(3):340–348. 10.1134/S1061920806030095
-functions related to generalized twisted Bernoulli numbers. Russian Journal of Mathematical Physics 2006,13(3):340–348. 10.1134/S1061920806030095Simsek Y: Hardy character sums related to Eisenstein series and theta functions. Advanced Studies in Contemporary Mathematics 2006,12(1):39–53.
Simsek Y: Remarks on reciprocity laws of the Dedekind and Hardy sums. Advanced Studies in Contemporary Mathematics 2006,12(2):237–246.
Simsek Y: Twisted (
 ,
,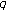 )-Bernoulli numbers and polynomials related to twisted (
)-Bernoulli numbers and polynomials related to twisted ( ,
, )-zeta function and
)-zeta function and 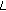 -function. Journal of Mathematical Analysis and Applications 2006,324(2):790–804. 10.1016/j.jmaa.2005.12.057
-function. Journal of Mathematical Analysis and Applications 2006,324(2):790–804. 10.1016/j.jmaa.2005.12.057Simsek Y: On twisted
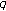 -Hurwitz zeta function and
-Hurwitz zeta function and 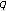 -two-variable
-two-variable 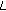 -function. Applied Mathematics and Computation 2007,187(1):466–473. 10.1016/j.amc.2006.08.146
-function. Applied Mathematics and Computation 2007,187(1):466–473. 10.1016/j.amc.2006.08.146Simsek Y: The behavior of the twisted
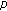 -adic (
-adic (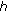 ,
, )-
)-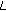 -functions at
-functions at 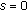 -functions at . Journal of the Korean Mathematical Society 2007,44(4):915–929. 10.4134/JKMS.2007.44.4.915
-functions at . Journal of the Korean Mathematical Society 2007,44(4):915–929. 10.4134/JKMS.2007.44.4.915Simsek Y: Generating functions of the twisted Bernoulli numbers and polynomials associated with their interpolation functions. Advanced Studies in Contemporary Mathematics 2008,16(2):251–278.
Simsek Y, Kim D, Rim S-H: On the two-variable Dirichlet
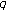 -
- -series. Advanced Studies in Contemporary Mathematics 2005,10(2):131–142.
-series. Advanced Studies in Contemporary Mathematics 2005,10(2):131–142.Simsek Y, Mehmet A: Remarks on Dedekind eta function, theta functions and Eisenstein series under the Hecke operators. Advanced Studies in Contemporary Mathematics 2005,10(1):15–24.
Ozden H, Cangul IN, Simsek Y: On the behavior of two variable twisted -adic Euler --functions. Nonlinear Analysis. In press Nonlinear Analysis. In press
Simsek Y, Yang S: Transformation of four Titchmarsh-type infinite integrals and generalized Dedekind sums associated with Lambert series. Advanced Studies in Contemporary Mathematics 2004,9(2):195–202.
Carlitz L:
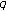 -Bernoulli and Eulerian numbers. Transactions of the American Mathematical Society 1954, 76: 332–350.
-Bernoulli and Eulerian numbers. Transactions of the American Mathematical Society 1954, 76: 332–350.Cenkci M, Can M: Some results on
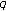 -analogue of the Lerch zeta function. Advanced Studies in Contemporary Mathematics 2006,12(2):213–223.
-analogue of the Lerch zeta function. Advanced Studies in Contemporary Mathematics 2006,12(2):213–223.Cenkci M, Simsek Y, Kurt V: Further remarks on multiple
 -adic
-adic 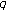 -
- -function of two variables. Advanced Studies in Contemporary Mathematics 2007,14(1):49–68.
-function of two variables. Advanced Studies in Contemporary Mathematics 2007,14(1):49–68.Dąbrowski A: A note on
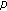 -adic
-adic 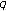 -
-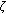 -functions. Journal of Number Theory 1997,64(1):100–103. 10.1006/jnth.1997.2107
-functions. Journal of Number Theory 1997,64(1):100–103. 10.1006/jnth.1997.2107Fox GJ: A
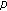 -adic
-adic 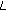 -function of two variables. L'Enseignement Mathématique, IIe Série 2000,46(3–4):225–278.
-function of two variables. L'Enseignement Mathématique, IIe Série 2000,46(3–4):225–278.Jang L-C, Kim S-D, Park D-W, Ro Y-S: A note on Euler number and polynomials. Journal of Inequalities and Applications 2006, 2006:-5.
Jang L-C, Kurt V, Simsek Y, Rim SH:
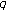 -analogue of the
-analogue of the  -adic twisted
-adic twisted  -function. Journal of Concrete and Applicable Mathematics 2008,6(2):169–176.
-function. Journal of Concrete and Applicable Mathematics 2008,6(2):169–176.Koblitz N: On Carlitz's
 -Bernoulli numbers. Journal of Number Theory 1982,14(3):332–339. 10.1016/0022-314X(82)90068-3
-Bernoulli numbers. Journal of Number Theory 1982,14(3):332–339. 10.1016/0022-314X(82)90068-3Park KH, Kim Y-H: On some arithmetical properties of the Genocchi numbers and polynomials. Advances in Difference Equations 2008, -14.
Rim S-H, Park KH, Moon EJ: On Genocchi numbers and polynomials. Abstract and Applied Analysis 2008, 2008:-7.
Schikhof WH: Ultrametric Calculus: An Introduction to p-Adic Analysis, Cambridge Studies in Advanced Mathematics. Volume 4. Cambridge University Press, Cambridge, UK; 1984:viii+306.
Shiratani K, Yamamoto S: On a
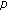 -adic interpolation function for the Euler numbers and its derivatives. Memoirs of the Faculty of Science, Kyushu University. Series A 1985,39(1):113–125. 10.2206/kyushumfs.39.113
-adic interpolation function for the Euler numbers and its derivatives. Memoirs of the Faculty of Science, Kyushu University. Series A 1985,39(1):113–125. 10.2206/kyushumfs.39.113Srivastava HM, Kim T, Simsek Y:
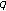 -Bernoulli numbers and polynomials associated with multiple
-Bernoulli numbers and polynomials associated with multiple 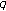 -zeta functions and basic
-zeta functions and basic  -series. Russian Journal of Mathematical Physics 2005,12(2):241–268.
-series. Russian Journal of Mathematical Physics 2005,12(2):241–268.Washington LC: Introduction to Cyclotomic Fields, Graduate Texts in Mathematics. Volume 83. 2nd edition. Springer, New York, NY, USA; 1997:xiv+487.
Woodcock CF: Special
 -adic analytic functions and Fourier transforms. Journal of Number Theory 1996,60(2):393–408. 10.1006/jnth.1996.0130
-adic analytic functions and Fourier transforms. Journal of Number Theory 1996,60(2):393–408. 10.1006/jnth.1996.0130Young PT: On the behavior of some two-variable
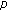 -adic
-adic 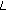 -functions. Journal of Number Theory 2003,98(1):67–88. 10.1016/S0022-314X(02)00031-8
-functions. Journal of Number Theory 2003,98(1):67–88. 10.1016/S0022-314X(02)00031-8Zhao J: Multiple
 -zeta functions and multiple
-zeta functions and multiple 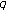 -polylogarithms. Ramanujan Journal 2007,14(2):189–221. 10.1007/s11139-007-9025-9
-polylogarithms. Ramanujan Journal 2007,14(2):189–221. 10.1007/s11139-007-9025-9
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Park, K.H. On Interpolation Functions of the Generalized Twisted 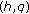 -Euler Polynomials.
J Inequal Appl 2009, 946569 (2009). https://doi.org/10.1155/2009/946569
-Euler Polynomials.
J Inequal Appl 2009, 946569 (2009). https://doi.org/10.1155/2009/946569
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/946569
 -Euler Numbers and Polynomials
-Euler Numbers and Polynomials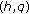 -Euler-Zeta Function and
-Euler-Zeta Function and 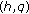 -
-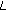 -Function
-Function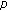 -Adic Twisted Two-Variable Euler
-Adic Twisted Two-Variable Euler  -L-Functions
-L-Functions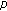 -adic interpolation of the generalized Euler numbers and its applications. Tokyo Journal of Mathematics 1987,10(2):281–293. 10.3836/tjm/1270134514
-adic interpolation of the generalized Euler numbers and its applications. Tokyo Journal of Mathematics 1987,10(2):281–293. 10.3836/tjm/1270134514 -analogue of the
-analogue of the  -adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320–329. 10.1006/jnth.1999.2373
-adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320–329. 10.1006/jnth.1999.2373 -Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288–299.
-Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288–299. -Riemann zeta function. International Journal of Mathematics and Mathematical Sciences 2004,2004(12):599–605. 10.1155/S0161171204307180
-Riemann zeta function. International Journal of Mathematics and Mathematical Sciences 2004,2004(12):599–605. 10.1155/S0161171204307180 -zeta functions and their values at negative integers. Russian Journal of Mathematical Physics 2004,11(1):71–76.
-zeta functions and their values at negative integers. Russian Journal of Mathematical Physics 2004,11(1):71–76. -analog of the two-variable
-analog of the two-variable  -adic
-adic  -function. Russian Journal of Mathematical Physics 2005,12(2):186–196.
-function. Russian Journal of Mathematical Physics 2005,12(2):186–196. -generalized Euler numbers and polynomials. Russian Journal of Mathematical Physics 2006,13(3):293–298. 10.1134/S1061920806030058
-generalized Euler numbers and polynomials. Russian Journal of Mathematical Physics 2006,13(3):293–298. 10.1134/S1061920806030058 -adic
-adic  -
-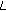 -functions. Advanced Studies in Contemporary Mathematics 2006,12(1):61–72.
-functions. Advanced Studies in Contemporary Mathematics 2006,12(1):61–72.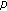 -adic invariant integral in the rings of
-adic invariant integral in the rings of 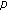 -adic integers. Advanced Studies in Contemporary Mathematics 2006,13(1):95–99.
-adic integers. Advanced Studies in Contemporary Mathematics 2006,13(1):95–99. -adic
-adic 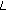 -function. Russian Journal of Mathematical Physics 2006,13(2):151–157. 10.1134/S1061920806020038
-function. Russian Journal of Mathematical Physics 2006,13(2):151–157. 10.1134/S1061920806020038 -extension of the Euler formula and trigonometric functions. Russian Journal of Mathematical Physics 2007,14(3):275–278. 10.1134/S1061920807030041
-extension of the Euler formula and trigonometric functions. Russian Journal of Mathematical Physics 2007,14(3):275–278. 10.1134/S1061920807030041 -adic
-adic  -integral on
-integral on  at
at 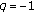 . Journal of Mathematical Analysis and Applications 2007,331(2):779–792. 10.1016/j.jmaa.2006.09.027
. Journal of Mathematical Analysis and Applications 2007,331(2):779–792. 10.1016/j.jmaa.2006.09.027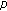 -adic
-adic 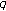 -
- -functions and sums of powers. Journal of Mathematical Analysis and Applications 2007,329(2):1472–1481. 10.1016/j.jmaa.2006.07.071
-functions and sums of powers. Journal of Mathematical Analysis and Applications 2007,329(2):1472–1481. 10.1016/j.jmaa.2006.07.071 -extension of Euler and Genocchi numbers. Journal of Mathematical Analysis and Applications 2007,326(2):1458–1465. 10.1016/j.jmaa.2006.03.037
-extension of Euler and Genocchi numbers. Journal of Mathematical Analysis and Applications 2007,326(2):1458–1465. 10.1016/j.jmaa.2006.03.037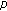 -adic
-adic 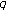 -integral on
-integral on 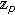 associated with
associated with 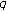 -Euler numbers. Advanced Studies in Contemporary Mathematics 2007,15(2):133–137.
-Euler numbers. Advanced Studies in Contemporary Mathematics 2007,15(2):133–137. -Euler numbers and polynomials associated with
-Euler numbers and polynomials associated with 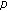 -adic
-adic  -integrals. Journal of Nonlinear Mathematical Physics 2007,14(1):15–27. 10.2991/jnmp.2007.14.1.3
-integrals. Journal of Nonlinear Mathematical Physics 2007,14(1):15–27. 10.2991/jnmp.2007.14.1.3 -Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51–57.
-Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51–57.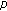 -adic interpolating function for
-adic interpolating function for 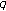 -Euler numbers and its derivatives. Journal of Mathematical Analysis and Applications 2008,339(1):598–608. 10.1016/j.jmaa.2007.07.027
-Euler numbers and its derivatives. Journal of Mathematical Analysis and Applications 2008,339(1):598–608. 10.1016/j.jmaa.2007.07.027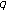 -Euler numbers and polyomials. Advanced Studies in Contemporary Mathematics 2008,16(2):161–170.
-Euler numbers and polyomials. Advanced Studies in Contemporary Mathematics 2008,16(2):161–170.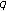 -Euler numbers and polynomials. Advanced Studies in Contemporary Mathematics 2008,16(2):161–170.
-Euler numbers and polynomials. Advanced Studies in Contemporary Mathematics 2008,16(2):161–170. -adic interpolation function for the
-adic interpolation function for the 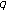 -adic interpolation function for the -extension of the generalized Bernoulli polynomials and its derivative. Discrete Mathematics 2009,309(6):1593–1602. 10.1016/j.disc.2008.03.001
-adic interpolation function for the -extension of the generalized Bernoulli polynomials and its derivative. Discrete Mathematics 2009,309(6):1593–1602. 10.1016/j.disc.2008.03.001 -Euler numbers and polynomials associated with fermionic
-Euler numbers and polynomials associated with fermionic 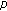 -adic
-adic 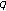 -integral on
-integral on  .Russian Journal of Mathematical Physics 2007,14(2):160–163. 10.1134/S1061920807020045
.Russian Journal of Mathematical Physics 2007,14(2):160–163. 10.1134/S1061920807020045 -Euler numbers and polynomials associated with basic
-Euler numbers and polynomials associated with basic 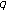 -
- -functions. Journal of Mathematical Analysis and Applications 2007,336(1):738–744. 10.1016/j.jmaa.2007.03.035
-functions. Journal of Mathematical Analysis and Applications 2007,336(1):738–744. 10.1016/j.jmaa.2007.03.035 ,
,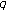 )-twisted Euler polynomials and numbers. Journal of Inequalities and Applications 2008, 2008:-8.
)-twisted Euler polynomials and numbers. Journal of Inequalities and Applications 2008, 2008:-8.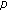 -adic
-adic 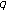 -Euler measure. General Mathematics 2007,15(2):24–37.
-Euler measure. General Mathematics 2007,15(2):24–37.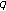 -Euler numbers and polynomials related to their interpolation functions. Applied Mathematics Letters 2008,21(9):934–939. 10.1016/j.aml.2007.10.005
-Euler numbers and polynomials related to their interpolation functions. Applied Mathematics Letters 2008,21(9):934–939. 10.1016/j.aml.2007.10.005 ,
, 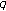 ) extension of twisted Euler polynomials and numbers. Acta Mathematica Hungarica 2008,120(3):281–299. 10.1007/s10474-008-7139-1
) extension of twisted Euler polynomials and numbers. Acta Mathematica Hungarica 2008,120(3):281–299. 10.1007/s10474-008-7139-1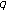 -Euler numbers and their applications. Abstract and Applied Analysis 2008, 2008:-16.
-Euler numbers and their applications. Abstract and Applied Analysis 2008, 2008:-16. -Euler numbers associated with the basic
-Euler numbers associated with the basic 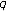 -zeta function. Applied Mathematics Letters 2007,20(4):366–369. 10.1016/j.aml.2006.04.019
-zeta function. Applied Mathematics Letters 2007,20(4):366–369. 10.1016/j.aml.2006.04.019 -function and twisted Bernoulli numbers. Advanced Studies in Contemporary Mathematics 2005,11(2):205–218.
-function and twisted Bernoulli numbers. Advanced Studies in Contemporary Mathematics 2005,11(2):205–218. -analogue of twisted
-analogue of twisted  -series and
-series and 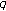 -twisted Euler numbers. Journal of Number Theory 2005,110(2):267–278. 10.1016/j.jnt.2004.07.003
-twisted Euler numbers. Journal of Number Theory 2005,110(2):267–278. 10.1016/j.jnt.2004.07.003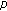 -adic twisted
-adic twisted  -
-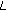 -functions related to generalized twisted Bernoulli numbers. Russian Journal of Mathematical Physics 2006,13(3):340–348. 10.1134/S1061920806030095
-functions related to generalized twisted Bernoulli numbers. Russian Journal of Mathematical Physics 2006,13(3):340–348. 10.1134/S1061920806030095 ,
,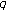 )-Bernoulli numbers and polynomials related to twisted (
)-Bernoulli numbers and polynomials related to twisted ( ,
, )-zeta function and
)-zeta function and 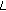 -function. Journal of Mathematical Analysis and Applications 2006,324(2):790–804. 10.1016/j.jmaa.2005.12.057
-function. Journal of Mathematical Analysis and Applications 2006,324(2):790–804. 10.1016/j.jmaa.2005.12.057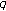 -Hurwitz zeta function and
-Hurwitz zeta function and 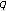 -two-variable
-two-variable 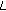 -function. Applied Mathematics and Computation 2007,187(1):466–473. 10.1016/j.amc.2006.08.146
-function. Applied Mathematics and Computation 2007,187(1):466–473. 10.1016/j.amc.2006.08.146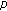 -adic (
-adic (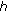 ,
, )-
)-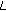 -functions at
-functions at 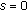 -functions at . Journal of the Korean Mathematical Society 2007,44(4):915–929. 10.4134/JKMS.2007.44.4.915
-functions at . Journal of the Korean Mathematical Society 2007,44(4):915–929. 10.4134/JKMS.2007.44.4.915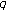 -
- -series. Advanced Studies in Contemporary Mathematics 2005,10(2):131–142.
-series. Advanced Studies in Contemporary Mathematics 2005,10(2):131–142.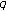 -Bernoulli and Eulerian numbers. Transactions of the American Mathematical Society 1954, 76: 332–350.
-Bernoulli and Eulerian numbers. Transactions of the American Mathematical Society 1954, 76: 332–350.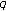 -analogue of the Lerch zeta function. Advanced Studies in Contemporary Mathematics 2006,12(2):213–223.
-analogue of the Lerch zeta function. Advanced Studies in Contemporary Mathematics 2006,12(2):213–223. -adic
-adic 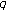 -
- -function of two variables. Advanced Studies in Contemporary Mathematics 2007,14(1):49–68.
-function of two variables. Advanced Studies in Contemporary Mathematics 2007,14(1):49–68.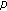 -adic
-adic 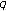 -
-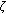 -functions. Journal of Number Theory 1997,64(1):100–103. 10.1006/jnth.1997.2107
-functions. Journal of Number Theory 1997,64(1):100–103. 10.1006/jnth.1997.2107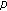 -adic
-adic  -function of two variables. L'Enseignement Mathématique, IIe Série 2000,46(3–4):225–278.
-function of two variables. L'Enseignement Mathématique, IIe Série 2000,46(3–4):225–278. -analogue of the
-analogue of the  -adic twisted
-adic twisted  -function. Journal of Concrete and Applicable Mathematics 2008,6(2):169–176.
-function. Journal of Concrete and Applicable Mathematics 2008,6(2):169–176. -Bernoulli numbers. Journal of Number Theory 1982,14(3):332–339. 10.1016/0022-314X(82)90068-3
-Bernoulli numbers. Journal of Number Theory 1982,14(3):332–339. 10.1016/0022-314X(82)90068-3 -adic interpolation function for the Euler numbers and its derivatives. Memoirs of the Faculty of Science, Kyushu University. Series A 1985,39(1):113–125. 10.2206/kyushumfs.39.113
-adic interpolation function for the Euler numbers and its derivatives. Memoirs of the Faculty of Science, Kyushu University. Series A 1985,39(1):113–125. 10.2206/kyushumfs.39.113 -Bernoulli numbers and polynomials associated with multiple
-Bernoulli numbers and polynomials associated with multiple 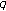 -zeta functions and basic
-zeta functions and basic  -series. Russian Journal of Mathematical Physics 2005,12(2):241–268.
-series. Russian Journal of Mathematical Physics 2005,12(2):241–268. -adic analytic functions and Fourier transforms. Journal of Number Theory 1996,60(2):393–408. 10.1006/jnth.1996.0130
-adic analytic functions and Fourier transforms. Journal of Number Theory 1996,60(2):393–408. 10.1006/jnth.1996.0130 -adic
-adic 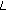 -functions. Journal of Number Theory 2003,98(1):67–88. 10.1016/S0022-314X(02)00031-8
-functions. Journal of Number Theory 2003,98(1):67–88. 10.1016/S0022-314X(02)00031-8 -zeta functions and multiple
-zeta functions and multiple 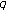 -polylogarithms. Ramanujan Journal 2007,14(2):189–221. 10.1007/s11139-007-9025-9
-polylogarithms. Ramanujan Journal 2007,14(2):189–221. 10.1007/s11139-007-9025-9