- Research Article
- Open access
- Published:
Abstract Convexity and Hermite-Hadamard Type Inequalities
Journal of Inequalities and Applications volume 2009, Article number: 943534 (2009)
Abstract
The deriving Hermite-Hadamard type inequalities for certain classes of abstract convex functions are considered totally, the inequalities derived for some of these classes before are summarized, new inequalities for others are obtained, and for one class of these functions the results on  are generalized to
are generalized to  . By considering a concrete area in
. By considering a concrete area in  , the derived inequalities are illustrated.
, the derived inequalities are illustrated.
1. Introduction
Studying Hermite-Hadamard type inequalities for some function classes has been very important in recent years. These inequalities which are well known for convex functions have been also found in different function classes (see [1–5]).
Abstract convex function is one of this type of function classes. Hermite-Hadamard type inequalities are studied for some important classes of abstract convex functions, and the concrete results are found [6–9]. For example, increasing convex-along-rays (ICAR) functions, which are defined in  , are considered in [8]. First, a correct inequality for these functions is given. For each
, are considered in [8]. First, a correct inequality for these functions is given. For each  there exists a number
there exists a number  such that
such that

for all 
Then, based on previous inequality the following inequality is proven. If  , then for all continuous ICAR function
, then for all continuous ICAR function

inequality is correct, where

and  is the area of domain
is the area of domain 
Similar inequalities are found for increasing positively homogenous (IPH) functions in [6], for increasing radiant (InR) functions in [9], and for increasing coradiant (ICR) functions in [7].
In this article, first, the theorem which yields inequality (1.1) is proven for ICAR functions defined on  , then the other inequalities are generalized, which based on this theorem.
, then the other inequalities are generalized, which based on this theorem.
Another generalization is made for  . A more covering set
. A more covering set  is considered and all results (for IPH, ICR, InR, ICAR functions) are examined for this set.
is considered and all results (for IPH, ICR, InR, ICAR functions) are examined for this set.
2. Abstract Convexity and Hermite-Hadamard Type Inequalities
Let  be a real line and
be a real line and  . Consider a set
. Consider a set  and a set
and a set  of functions
of functions  defined on
defined on  A function
A function  is called abstract convex with respect to
is called abstract convex with respect to  (or
(or  -convex) if there exists a set
-convex) if there exists a set  such that
such that

Clearly  is
is  -convex if and only if
-convex if and only if

Let  be a set of functions
be a set of functions  A set
A set  is called a supremal generator of the set
is called a supremal generator of the set  if each function
if each function  is abstract convex with respect to
is abstract convex with respect to 
2.1. Increasing Positively Homogeneous Functions and Hermite-Hadamard Type Inequalities
A function  defined on
defined on  is called increasing (with respect to the coordinate-wise order relation) if
is called increasing (with respect to the coordinate-wise order relation) if  implies that
implies that  .
.
The function  is positively homogeneous of degree one if
is positively homogeneous of degree one if

for all 
 and
and 
Let  be the set of all min-type functions defined on
be the set of all min-type functions defined on

that is, the set  consists of identical zero and all the functions of the form
consists of identical zero and all the functions of the form

with all 
One has that a function  is
is  convex if and only if
convex if and only if  is increasing and positively homogeneous of degree one (IPH) functions (see [10]).
is increasing and positively homogeneous of degree one (IPH) functions (see [10]).
The Hermite-Hadamard type inequalities are shown for IPH functions by using the following proposition which is very important for IPH functions.
Proposition 2.1.
Let  be an IPH function defined on
be an IPH function defined on  Then the following inequality holds for all
Then the following inequality holds for all  :
:

Proposition 2.2 can be easily shown by using the Proposition 2.1 (see [6]).
Proposition 2.2.
Let  be an IPH function, and let
be an IPH function, and let  be integrable on
be integrable on  Then
Then

for all  and this inequality is sharp.
and this inequality is sharp.
Unlike the previous work, inequality (2.7) (obtained for IPH functions) and inequalities in the type of (2.7) (will be obtained for different function classes) are going to be inquired for more general the  sets not for the
sets not for the  set.
set.  will be certainly different for each function class.
will be certainly different for each function class.
Let  be a closed domain, that is,
be a closed domain, that is,  and let
and let  be positive number. Let
be positive number. Let  be the set of all points
be the set of all points  such that
such that

where 
In the case of  will be the set
will be the set  in [8, 9].
in [8, 9].
In [6, Proposition 3.2], the proposition has been given for  , the same proposition is defined for
, the same proposition is defined for  as follows, and its proof is similar.
as follows, and its proof is similar.
Proposition 2.3.
Let  be an IPH function defined on
be an IPH function defined on  If the set
If the set  is nonempty and
is nonempty and  is integrable on
is integrable on  , then
, then

We had proved a proposition in [6] by using a function  and we get a right-hand side inequality, similar to (2.7).
and we get a right-hand side inequality, similar to (2.7).
Proposition 2.4.
Let  be an IPH function, and let
be an IPH function, and let  be integrable function on
be integrable function on  Then
Then

For every  the inequality
the inequality

is sharp.
2.2. Increasing Positively Homogeneous Functions and Hermite-Hadamard Type Inequalities
A function  is called increasing radiant (InR) function if
is called increasing radiant (InR) function if
(1) is increasing;
is increasing;
(2) is radiant; that is,
is radiant; that is,  for all
for all  , and
, and 
Consider the coupling function  defined on
defined on 

Denote by  the function defined on
the function defined on  by the formula
by the formula

It is known that the set

is supremal generator of all increasing radiant functions defined on  (see[9])
(see[9])
Note that for  we get
we get  .
.
The very important property for InR functions is given here in after. It can be easily proved.
Proposition 2.5.
Let  be an InR function defined on
be an InR function defined on  Then the following inequality holds for all
Then the following inequality holds for all  :
:

By using [9, Proposition 2.5], the following proposition is proved.
Proposition 2.6.
Let  be InR functions and integrable on
be InR functions and integrable on  . Then
. Then

for all  This inequality is sharp for any
This inequality is sharp for any  since one has the inequality in [9] for
since one has the inequality in [9] for 
We determine the set  for InR functions. Let
for InR functions. Let  be the set of all points
be the set of all points  such that
such that

which is given in [9, Proposition 3.1] can be generalized for  .
.
Proposition 2.7.
Let  be an InR function defined on
be an InR function defined on  If the set
If the set  is nonempty and
is nonempty and  is integrable on
is integrable on  then
then

Proof.
The proof of the proposition can be made in a similar way to the proof in [9, Proposition 3.1].
Now, we will study to achieve right-hand side inequality for InR functions.
First, Let us prove the auxiliary proposition.
Proposition 2.8.
Let  be an InR function on
be an InR function on  Then the following inequalities hold for all
Then the following inequalities hold for all  :
:

where

Proof.
Since  is InR function on
is InR function on  then
then

for all  From this
From this

That is,

If we consider the definition of  then
then

for all 
Proposition 2.9.
Let  be an InR function and integrable on
be an InR function and integrable on  ,
,  and
and

then

holds and is sharp since we get equality for 
Proof.
It follows from Proposition 2.8.
Corollary 2.10.
Let  be an InR function and integrable on
be an InR function and integrable on  If
If  and
and  for all
for all  then
then

holds and is sharp.
2.3. Increasing Coradiant Functions and Hermit-Hadamard Type Inequalities
A function  defined on a cone
defined on a cone  is called coradiant if
is called coradiant if

It is easy to check that  is coradiant if and only if
is coradiant if and only if

We will consider increasing coradiant (ICR) function defined on the cone 
Consider the function  defined on
defined on 

where 
Recall that the set

is supremal generator of the class ICR functions defined on  (see [10]).
(see [10]).
The Hermit-Hadamard type inequalities have been obtained for ICR functions by using the following proposition in [7].
Proposition 2.11.
Let  be an ICR function defined on
be an ICR function defined on  Then the following inequality holds for all
Then the following inequality holds for all  :
:

Proposition 2.12.
Let  be ICR function and integrable on
be ICR function and integrable on  Then the following inequality holds for all
Then the following inequality holds for all  :
:

and it is sharp.
The set  is defined for ICR function, namely,
is defined for ICR function, namely,  denotes the set of all points
denotes the set of all points  such that
such that

Proposition 2.13.
Let  be an ICR function on
be an ICR function on  If the set
If the set  is nonempty and
is nonempty and  is integrable on
is integrable on  , then
, then

Let us define a new function  such that
such that

where  is max-type function. By including the new function
is max-type function. By including the new function  , we can achieve right-hand side inequalities for ICR functions, too.
, we can achieve right-hand side inequalities for ICR functions, too.
Proposition 2.14.
Let function  be an ICR function and integrable on
be an ICR function and integrable on  Then
Then

and for every  the inequality
the inequality

is sharp.
2.4. Increasing Convex Along Rays Functions and Hermit-HadamardType Inequalities
The Hermite-Hadamard type inequalities are studied for ICAR functions in [8]. But only the functions which are defined on  are considered.
are considered.
In this article, the functions which are defined on  are considered, and general results are found.
are considered, and general results are found.
Let  be a conic set. A function
be a conic set. A function  is called convex-along-rays if its restriction to each ray starting from zero is a convex function of one variable. In other words, it means that the function
is called convex-along-rays if its restriction to each ray starting from zero is a convex function of one variable. In other words, it means that the function

is convex for each 
In this paper we consider increasing convex-along- rays (ICARs) functions defined on 
It is known that a finite ICAR function is continuous on the  and lower semicontinuous on
and lower semicontinuous on  in [10].
in [10].
Let us give two theorems which had been proved in [10, Theorems 3.2 and 3.4].
Theorem 2.15.
Let  be the class of all functions
be the class of all functions  defined by
defined by

where  is a min-type function and
is a min-type function and  A function
A function  is
is  -convex if and only if
-convex if and only if  is lower semicontinuous and ICAR.
is lower semicontinuous and ICAR.
Theorem 2.16.
Let  be ICAR function, and let
be ICAR function, and let  be a point such that
be a point such that  for some
for some  Then the sup differential
Then the sup differential

is not empty and

where 
Now, we can define the following theorem which is important to achieve Hermit-Hadamard type inequalities for ICAR functions.
Theorem 2.17.
Let  be a finite ICAR function defined on
be a finite ICAR function defined on  Then for each
Then for each  there exists a number
there exists a number  such that
such that

for all 
Proof.
The result follows directly from Theorem 2.16
We will apply Theorem 2.17 in the study of Hermit-Hadamard type inequalities for ICAR functions.
Proposition 2.18.
Let  ,
,  be ICAR function. Then the following inequality holds for all
be ICAR function. Then the following inequality holds for all  :
:

Proof.
It follows from Theorem 2.17.
Formula (2.44) can be made simply with the sets  .
.
Let  be a bounded set such that
be a bounded set such that  and
and

Proposition 2.19.
Let the set  be nonempty, and let
be nonempty, and let  be a continuous ICAR function defined on
be a continuous ICAR function defined on  Then the following inequality holds:
Then the following inequality holds:

Proof.
Let  It follows from (2.43) and the definition of
It follows from (2.43) and the definition of  that
that

Thus

Since  is compact (see [8]) and
is compact (see [8]) and  is continuous (finite ICAR functions is continuous), it follows that the maximum in (2.46) is attained.
is continuous (finite ICAR functions is continuous), it follows that the maximum in (2.46) is attained.
Remark 2.20.
Inequalities (2.9), (2.18), (2.35), and (2.46), which are obtained for different convex classes, are actually different, even if they appear to be the same. The reason is that these are determined with the (2.8), (2.17), (2.34), and (2.45) formulas appropriate for the sets of  and also yielding different sets.
and also yielding different sets.
3. Examples
The results of different classes of convex functions are defined for same triangle region 

The inequalities (2.7) and (2.10) have been defined for IPH functions. The inequalities are examined for the region  in [6]. If we combine two results, then we get
in [6]. If we combine two results, then we get

for all 
If we study the set  for IPH functions, a point
for IPH functions, a point  belongs to
belongs to  if and only if
if and only if

That is, the set  is intersection with the set
is intersection with the set  and the parabola by formula (3.3).
and the parabola by formula (3.3).
Let us consider the InR functions for same region  The inequality (2.16) has been examined for
The inequality (2.16) has been examined for  and the following inequality has been obtained in [9]:
and the following inequality has been obtained in [9]:

for all 
Let us study on the right-hand side inequality (2.26), which is obtained in this article, for same region  , which has been defined as follows:
, which has been defined as follows:

for all 
We will separate two sets:

such that 
In this case, we get

Thus, the inequality (2.26) becomes

for all  it is held.
it is held.
The set  can be defined for InR functions such that, a point
can be defined for InR functions such that, a point  belongs to
belongs to  if and only if
if and only if

The inequalities (2.33) and (2.35) had been obtained for ICR functions. If these inequalities are examined for the same triangle region  then the following inequality is obtained in [7]:
then the following inequality is obtained in [7]:

for all 
The set  has been obtained for ICR functions as formula (2.34). Formula (2.34) becomes formula (3.11) for the triangle region
has been obtained for ICR functions as formula (2.34). Formula (2.34) becomes formula (3.11) for the triangle region  That is a point
That is a point  belongs to
belongs to  if and only if
if and only if

Lastly, formula (2.44) has been defined for ICAR functions. Now, we will define the same formula for the triangle region  :
:

and the inequality is held for all  , where
, where  is parameter which depends on
is parameter which depends on  (see [10]).
(see [10]).
ICAR functions had been studied for the set  which is determined by formula (2.45). If
which is determined by formula (2.45). If  in
in  , then the set
, then the set  is special case of the given formula (2.8). Then a point
is special case of the given formula (2.8). Then a point  belongs to
belongs to  if and only if
if and only if

In other words,  belongs to the parabola by formula (3.13).
belongs to the parabola by formula (3.13).
4. Conclusion
Hermite-Hadamard type inequalities are investigated for specific functions classes. One of these functions classes is abstract convex functions. The deriving Hermite-Hadamard type inequalities for IPH, InR, ICR, and ICAR functions, which are important classes of abstract convex functions, are investigated by different authors [6–10].
In this article, this problem is considered entirely; findings from [6–10] are summarized; new results are found for some classes; results of some classes are generalized. For example, all results are found for more general  case, not all for
case, not all for  . Even though the results, (2.9), (2.18), (2.35), (2.46), are similar in appearance, they represent different inequalities, since the sets, which are defined with formulas (2.8), (2.17), (2.34), and (2.45), for different classes, are different.
. Even though the results, (2.9), (2.18), (2.35), (2.46), are similar in appearance, they represent different inequalities, since the sets, which are defined with formulas (2.8), (2.17), (2.34), and (2.45), for different classes, are different.
Right-hand side inequalities, which are found for InR functions classes in [9], are considered here as well; more general results are found with the support of  functions and explained as Proposition 2.9.
functions and explained as Proposition 2.9.
ICAR functions, which are studied in [8], are investigated on  here, and results are explained in Proposition 2.18 . The inequality, which is explained in formula (2.44), is a new inequality for these functions classes.
here, and results are explained in Proposition 2.18 . The inequality, which is explained in formula (2.44), is a new inequality for these functions classes.
Finally, all the results are explained for the same region given on  . Formulas (3.2), (3.8), (3.10), and (3.12) are concrete results of Hermit-Hadamard type inequalities of different abstract convex function classes on given triangle region. Formulas (3.3), (3.9), (3.11), and (3.13) are concrete explanations of
. Formulas (3.2), (3.8), (3.10), and (3.12) are concrete results of Hermit-Hadamard type inequalities of different abstract convex function classes on given triangle region. Formulas (3.3), (3.9), (3.11), and (3.13) are concrete explanations of  sets in this region.
sets in this region.
References
Dragomir SS, Pearce CEM: Quasi-convex functions and Hadamard's inequality. Bulletin of the Australian Mathematical Society 1998,57(3):377–385. 10.1017/S0004972700031786
Dragomir SS, Pečarić J, Persson LE: Some inequalities of Hadamard type. Soochow Journal of Mathematics 1995,21(3):335–341.
Gill PM, Pearce CEM, Pečarić J: Hadamard's inequality for -convex functions. Journal of Mathematical Analysis and Applications 1997,215(2):461–470. 10.1006/jmaa.1997.5645
Pearce CEM, Rubinov AM:
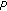 -functions, quasi-convex functions, and Hadamard-type inequalities. Journal of Mathematical Analysis and Applications 1999,240(1):92–104. 10.1006/jmaa.1999.6593
-functions, quasi-convex functions, and Hadamard-type inequalities. Journal of Mathematical Analysis and Applications 1999,240(1):92–104. 10.1006/jmaa.1999.6593Rubinov AM, Dutta J: Hadamard type inequality for quasiconvex functions in higher dimensions. Journal of Analysis and Applications 2002, 270: 80–91. 10.1016/S0022-247X(02)00050-1
Adilov GR, Kemali S: Hermite-Hadamard-type inequalities for increasing positively homogeneous functions. Journal of Inequalities and Applications 2007, 2007:-10.
Adilov GR: Increasing co-radiant functions and Hermite-Hadamard type inequalities. to apprear in Mathematical Inequalities and Applications to apprear in Mathematical Inequalities and Applications
Dragomir SS, Dutta J, Rubinov AM: Hermite-Hadamard-type inequalities for increasing convex-along-rays functions. Analysis 2004,24(2):171–181.
Sharikov EV: Hermite-Hadamard type inequalities for increasing radiant functions. Journal of Inequalities in Pure and Applied Mathematics 2003.,4(2, article 47):
Rubinov A: Abstract Convexity and Global Optimization, Nonconvex Optimization and Its Applications. Volume 44. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2000:xviii+490.
Acknowledgments
The first author was supported by the Scientific Research Project Administration Unit of Mersin University (Turkey). The second author was supported by the Scientific Research Project Administration Unit of Akdeniz University (Turkey).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Adilov, G.R., Kemali, S. Abstract Convexity and Hermite-Hadamard Type Inequalities. J Inequal Appl 2009, 943534 (2009). https://doi.org/10.1155/2009/943534
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/943534
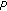 -functions, quasi-convex functions, and Hadamard-type inequalities. Journal of Mathematical Analysis and Applications 1999,240(1):92–104. 10.1006/jmaa.1999.6593
-functions, quasi-convex functions, and Hadamard-type inequalities. Journal of Mathematical Analysis and Applications 1999,240(1):92–104. 10.1006/jmaa.1999.6593