- Research Article
- Open access
- Published:
Existence and Asymptotic Behavior of Solutions for Weighted  -Laplacian System Multipoint Boundary Value Problems in Half Line
-Laplacian System Multipoint Boundary Value Problems in Half Line
Journal of Inequalities and Applications volume 2009, Article number: 926518 (2009)
Abstract
This paper investigates the existence and asymptotic behavior of solutions for weighted  -Laplacian system multipoint boundary value problems in half line. When the nonlinearity term
-Laplacian system multipoint boundary value problems in half line. When the nonlinearity term  satisfies sub-(
satisfies sub-( ) growth condition or general growth condition, we give the existence of solutions via Leray-Schauder degree.
) growth condition or general growth condition, we give the existence of solutions via Leray-Schauder degree.
1. Introduction
In this paper, we consider the existence and asymptotic behavior of solutions for the following weighted  -Laplacian system:
-Laplacian system:


where  exists and
exists and  ,
,  is called the weighted
is called the weighted  -Laplacian;
-Laplacian;  satisfies
satisfies  and
and  ; the equivalent
; the equivalent  means that
means that  and
and  both exist and equal;
both exist and equal;  is a positive parameter.
is a positive parameter.
The study of differential equations and variational problems with variable exponent growth conditions is a new and interesting topic. Many results have been obtained on these kinds of problems, for example, [1–15]. We refer to [2, 16, 17], the applied background on these problems. If  and
and  (a constant),
(a constant),  is the well-known
is the well-known  -Laplacian. If
-Laplacian. If  is a general function,
is a general function,  represents a nonhomogeneity and possesses more nonlinearity, and thus
represents a nonhomogeneity and possesses more nonlinearity, and thus  is more complicated than
is more complicated than  . For example, We have the following.
. For example, We have the following.
(1)If  is a bounded domain, the Rayleigh quotient
is a bounded domain, the Rayleigh quotient

is zero in general, and only under some special conditions  (see [6]), but the fact that
(see [6]), but the fact that  is very important in the study of
is very important in the study of  -Laplacian problems;
-Laplacian problems;
(2)If  and
and  (a constant) and
(a constant) and  , then
, then  is concave; this property is used extensively in the study of one dimensional
is concave; this property is used extensively in the study of one dimensional  -Laplacian problems, but it is invalid for
-Laplacian problems, but it is invalid for  . It is another difference on
. It is another difference on  and
and  .
.
(3)On the existence of solutions of the following typical  problem;
problem;

because of the nonhomogeneity of  , and if
, and if  then the corresponding functional is coercive, if
then the corresponding functional is coercive, if  then the corresponding functional can satisfy Palais-Smale condition, (see [4, 7]). If
then the corresponding functional can satisfy Palais-Smale condition, (see [4, 7]). If  there are more difficulties to testify that the corresponding functional is coercive or satisfying Palais-Smale conditions, and the results on this case are rare.
there are more difficulties to testify that the corresponding functional is coercive or satisfying Palais-Smale conditions, and the results on this case are rare.
There are many results on the existence of solutions for  -Laplacian equation with multi-point boundary value conditions (see [18–21]). On the existence of solutions for
-Laplacian equation with multi-point boundary value conditions (see [18–21]). On the existence of solutions for  -Laplacian systems boundary value problems, we refer to [5, 7, 10–15]. But results on the existence and asymptotic behavior of solutions for weighted
-Laplacian systems boundary value problems, we refer to [5, 7, 10–15]. But results on the existence and asymptotic behavior of solutions for weighted  -Laplacian systems with multi-point boundary value conditions are rare. In this paper, when
-Laplacian systems with multi-point boundary value conditions are rare. In this paper, when  is a general function, we investigate the existence and asymptotic behavior of solutions for weighted
is a general function, we investigate the existence and asymptotic behavior of solutions for weighted  -Laplacian systems with multi-point boundary value conditions. Moreover, the case of
-Laplacian systems with multi-point boundary value conditions. Moreover, the case of  has been discussed.
has been discussed.
Let  and
and  ,
, ; the function
; the function  is assumed to be Caratheodory, by this we mean that
is assumed to be Caratheodory, by this we mean that
(i)for almost every  , the function
, the function  is continuous;
is continuous;
(ii)for each  , the function
, the function  is measurable on
is measurable on  ;
;
(iii)for each  there is a
there is a  such that, for almost every
such that, for almost every  and every
and every  with
with  ,
,  , one has
, one has

Throughout the paper, we denote

The inner product in  will be denoted by
will be denoted by  will denote the absolute value and the Euclidean norm on
will denote the absolute value and the Euclidean norm on  . Let
. Let  denote the space of absolutely continuous functions on the interval
denote the space of absolutely continuous functions on the interval  . For
. For  we set
we set  ,
,  . For any
. For any  , we denote
, we denote  ,
,  and
and  . Spaces
. Spaces  and
and  will be equipped with the norm
will be equipped with the norm  and
and  , respectively. Then
, respectively. Then  and
and  are Banach spaces. Denote
are Banach spaces. Denote  the norm
the norm 
We say a function  is a solution of (1.1) if
is a solution of (1.1) if  with
with  absolutely continuous on (
absolutely continuous on ( ,
, ), which satisfies (1.1) almost every on
), which satisfies (1.1) almost every on  .
.
In this paper, we always use  to denote positive constants, if it cannot lead to confusion. Denote
to denote positive constants, if it cannot lead to confusion. Denote

We say  satisfies sub-(
satisfies sub-( ) growth condition, if
) growth condition, if  satisfies
satisfies

where  , and
, and  . We say
. We say  satisfies general growth condition, if we don't know whether
satisfies general growth condition, if we don't know whether  satisfies sub-(
satisfies sub-( ) growth condition or not.
) growth condition or not.
We will discuss the existence of solutions of (1.1)-(1.2) in the following two cases
(i) satisfies sub-(
satisfies sub-( ) growth condition;
) growth condition;
(ii) satisfies general growth condition.
satisfies general growth condition.
This paper is divided into four sections. In the second section, we will do some preparation. In the third section, we will discuss the existence and asymptotic behavior of solutions of (1.1)-(1.2), when  satisfies sub-(
satisfies sub-( ) growth condition. Finally, in the fourth section, we will discuss the existence and asymptotic behavior of solutions of (1.1)-(1.2), when
) growth condition. Finally, in the fourth section, we will discuss the existence and asymptotic behavior of solutions of (1.1)-(1.2), when  satisfies general growth condition.
satisfies general growth condition.
2. Preliminary
For any  , denote
, denote  . Obviously,
. Obviously,  has the following properties.
has the following properties.
Lemma 2.1 (see [4]).

is a continuous function and satisfies
(i)For any  ,
,  is strictly monotone, that is,
is strictly monotone, that is,

(ii)There exists a function  as
as  , such that
, such that

It is well known that  is a homeomorphism from
is a homeomorphism from  to
to  for any fixed
for any fixed  . For any
. For any  , denote by
, denote by  the inverse operator of
the inverse operator of  , then
, then

It is clear that  is continuous and sends bounded sets into bounded sets. Let us now consider the following problem with boundary value condition (1.2):
is continuous and sends bounded sets into bounded sets. Let us now consider the following problem with boundary value condition (1.2):

where  and satisfies
and satisfies  . If
. If  is a solution of (2.4) with (1.2), by integrating (2.4) from
is a solution of (2.4) with (1.2), by integrating (2.4) from  to
to  , we find that
, we find that

Denote  . It is easy to see that
. It is easy to see that  is dependent on
is dependent on  . Define operator
. Define operator  as
as

By solving for  in (2.5) and integrating, we find that
in (2.5) and integrating, we find that

The boundary condition (1.2) implies that

For fixed  , we denote
, we denote

Throughout the paper, we denote  .
.
Lemma 2.2.
The function  has the following properties.
has the following properties.
(i)For any fixed  , the equation
, the equation

has a unique solution  .
.
(ii)The function  , defined in
, defined in  , is continuous and sends bounded sets to bounded sets. Moreover
, is continuous and sends bounded sets to bounded sets. Moreover

Proof.
-
(i)
From Lemma 2.1, it is immediate that
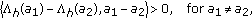 (2.12)
(2.12)
and hence, if (2.10) has a solution, then it is unique.
Let  . If
. If  , since
, since and
and  , it is easy to see that there exists an
, it is easy to see that there exists an  such that the
such that the  th component
th component  of
of  satisfies
satisfies  . Thus
. Thus  keeps sign on
keeps sign on  and
and

then

Thus the  th component
th component  of
of  is nonzero and keeps sign, and then we have
is nonzero and keeps sign, and then we have

Let us consider the equation

It is easy to see that all the solutions of (2.16) belong to  So, we have
So, we have

and it means the existence of solutions of  .
.
In this way, we define a function  , which satisfies
, which satisfies

-
(ii)
By the proof of (i), we also obtain
 sends bounded sets to bounded sets, and
sends bounded sets to bounded sets, and 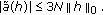 (2.19)
(2.19)
It only remains to prove the continuity of  . Let
. Let  be a convergent sequence in
be a convergent sequence in  and
and  as
as  . Since
. Since  is a bounded sequence, then it contains a convergent subsequence
is a bounded sequence, then it contains a convergent subsequence  . Let
. Let  as
as  . Since
. Since  , letting
, letting  , we have
, we have  . From (i), we get
. From (i), we get  , and it means that
, and it means that  is continuous. This completes the proof.
is continuous. This completes the proof.
Now, we define the operator  as
as

It is clear that  is continuous and sends bounded sets of
is continuous and sends bounded sets of  to bounded sets of
to bounded sets of  , and hence it is a compact continuous mapping.
, and hence it is a compact continuous mapping.
If  is a solution of (2.4) with (1.2), then
is a solution of (2.4) with (1.2), then

Let us define

where  and satisfies
and satisfies  ,
,  and we denote
and we denote  as
as

Lemma 2.3.
The operator  is continuous and sends equi-integrable sets in
is continuous and sends equi-integrable sets in  to relatively compact sets in
to relatively compact sets in  .
.
Proof.
It is easy to check that  . Since
. Since  and
and

it is easy to check that  is a continuous operator from
is a continuous operator from  to
to  .
.
Let now  be an equi-integrable set in
be an equi-integrable set in  , then there exists
, then there exists  , such that
, such that

We want to show that 
 is a compact set.
is a compact set.
Let  be a sequence in
be a sequence in  , then there exists a sequence
, then there exists a sequence  such that
such that  . For any
. For any  we have that
we have that

Hence the sequence  is equicontinuous.
is equicontinuous.
From the definition of  we have
we have  Thus
Thus

Thus  is uniformly bounded.
is uniformly bounded.
By Ascoli-Arzela theorem, there exists a subsequence of  (which we rename the same) being convergent in
(which we rename the same) being convergent in  . According to the bounded continuous of the operator
. According to the bounded continuous of the operator  , we can choose a subsequence of
, we can choose a subsequence of  (which we still denote
(which we still denote  is convergent in
is convergent in  , then
, then  is convergent in
is convergent in  .
.
Since

from the continuity of  and the integrability of
and the integrability of  in
in  , we can see that
, we can see that  is convergent in
is convergent in  . Thus that
. Thus that  is convergent in
is convergent in  .
.
This completes the proof.
We denote by  the Nemytski operator associated to
the Nemytski operator associated to  defined by
defined by

Lemma 2.4.

is a solution of (1.1)-(1.2) if and only if  is a solution of the following abstract equation:
is a solution of the following abstract equation:

Proof.
If  is a solution of (1.1)-(1.2), by integrating (1.1) from
is a solution of (1.1)-(1.2), by integrating (1.1) from  to
to  , we find that
, we find that

From (2.31), we have

From  , we have
, we have

So we have

Conversely, if  is a solution of (2.30), then
is a solution of (2.30), then

Thus  and
and  By the definition of the mapping
By the definition of the mapping  we have
we have

thus

From (2.30), we have

Obviously  from (2.38), we have
from (2.38), we have

Since  we have
we have  and
and

Hence  is a solutions of (1.1)-(1.2). This completes the proof.
is a solutions of (1.1)-(1.2). This completes the proof.
Lemma 2.5.
If  is a solution of (1.1)-(1.2), then for any
is a solution of (1.1)-(1.2), then for any  , there exists an
, there exists an  such that
such that  .
.
Proof.
If it is false, then  is strictly monotone in
is strictly monotone in  .
.
(i)If  is strictly decreasing in
is strictly decreasing in  , then
, then  ; it is a contradiction to
; it is a contradiction to 
(ii)If  is strictly increasing in
is strictly increasing in  , then
, then  ; it is a contradiction to
; it is a contradiction to 
This completes the proof.
3. 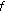 Satisfies Sub-(
Satisfies Sub-(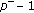 ) Growth Condition
) Growth Condition
In this section, we will apply Leray-Schauder's degree to deal with the existence of solutions for (1.1)-(1.2), when  satisfies sub-(
satisfies sub-( ) growth condition. Moreover, the asymptotic behavior has been discussed.
) growth condition. Moreover, the asymptotic behavior has been discussed.
Theorem 3.1.
Assume that  is an open bounded set in
is an open bounded set in  such that the following conditions hold.
such that the following conditions hold.
(10)For each  the problem
the problem

with boundary condition (1.2) has no solution on  .
.
(20)The equation

has no solution on  .
.
(30)The Brouwer degree  .
.
Then problems (1.1)-(1.2) have a solution on  .
.
Proof.
Let us consider the following equation with boundary value condition (1.2):

For any  observe that if
observe that if  is a solution to (3.1) with (1.2) or
is a solution to (3.1) with (1.2) or  is a solution to (3.3) with (1.2), we have necessarily
is a solution to (3.3) with (1.2), we have necessarily

It means that (3.1) with (1.2) and (3.3) with (1.2) have the same solutions for 
We denote  defined by
defined by

where  is defined by (2.29). Let
is defined by (2.29). Let

and the fixed point of  is a solution for (3.3) with (1.2). Also problem (3.3) with (1.2) can be written in the equivalent form
is a solution for (3.3) with (1.2). Also problem (3.3) with (1.2) can be written in the equivalent form

Since  is Caratheodory, it is easy to see that
is Caratheodory, it is easy to see that  is continuous and sends bounded sets into equi-integrable sets. It is easy to see that
is continuous and sends bounded sets into equi-integrable sets. It is easy to see that  is compact continuous. According to Lemmas 2.2 and 2.3, we can conclude that
is compact continuous. According to Lemmas 2.2 and 2.3, we can conclude that  is continuous and compact from
is continuous and compact from  to
to  for any
for any  . We assume that for
. We assume that for  , (3.7) does not have a solution on
, (3.7) does not have a solution on  ; otherwise we complete the proof. Now from hypothesis (10) it follows that (3.7) has no solutions for
; otherwise we complete the proof. Now from hypothesis (10) it follows that (3.7) has no solutions for  . For
. For  (3.3) is equivalent to the problem
(3.3) is equivalent to the problem

and if  is a solution to this problem, we must have
is a solution to this problem, we must have

Hence

where  is a constant. From Lemma 2.5, there exist
is a constant. From Lemma 2.5, there exist  such that
such that  ,
,  Hence
Hence  , it holds
, it holds  , a constant. Thus by (3.9)
, a constant. Thus by (3.9)

which together with hypothesis (20), implies that  Thus we have proved that (3.7) has no solution
Thus we have proved that (3.7) has no solution  on
on  then we get that for each
then we get that for each  , the Leray-Schauder degree
, the Leray-Schauder degree  is well defined for
is well defined for  , and from the properties of that degree, we have
, and from the properties of that degree, we have

Now it is clear that the problem

is equivalent to problem (1.1)-(1.2), and (3.12) tells us that problem (3.13) will have a solution if we can show that

Since

then

From Lemma 2.2, we have  . By the properties of the Leray-Schauder degree, we have
. By the properties of the Leray-Schauder degree, we have

where the function  is defined in (3.2) and
is defined in (3.2) and  denotes the Brouwer degree. By hypothesis (30), this last degree is different from zero. This completes the proof.
denotes the Brouwer degree. By hypothesis (30), this last degree is different from zero. This completes the proof.
Our next theorem is a consequence of Theorem 3.1. As an application of Theorem 3.1, let us consider the following equation with (1.2)

where  is Caratheodory,
is Caratheodory,  is continuous and Caratheodory, and for any fixed
is continuous and Caratheodory, and for any fixed  if
if  then
then  .
.
Theorem 3.2.
Assume that the following conditions hold
(10) for all
for all  and all
and all  where
where  satisfies
satisfies 
(20) for
for  uniformly
uniformly
(30)for large enough  , the equation
, the equation

has no solution on  , where
, where 
(40)the Brouwer degree  for large enough
for large enough  , where
, where 
Then problem (3.18) with (1.2) has at least one solution.
Proof.
Denote

At first, we consider the following problem:

According to the proof of Theorem 3.1, we know that (3.21) with (1.2) has the same solution of

where 
We claim that all the solutions of (3.21) are uniformly bounded for  . In fact, if it is false, we can find a sequence of solutions
. In fact, if it is false, we can find a sequence of solutions  for (3.21) with (1.2) such that
for (3.21) with (1.2) such that  as
as  , and
, and  for any
for any  .
.
Since  are solutions of (3.21) with (1.2), so
are solutions of (3.21) with (1.2), so  . According to Lemma 2.5, there exist
. According to Lemma 2.5, there exist  such that
such that  , then
, then

where  means the function which is uniformly convergent to 0 (as
means the function which is uniformly convergent to 0 (as  ). According to the property of
). According to the property of  and (3.23), then there exists a positive constant
and (3.23), then there exists a positive constant  such that
such that

then we have

Denote  , then
, then

Thus

Since  , from (3.27) we have
, from (3.27) we have

Denote  , then
, then  and
and  , then
, then  possesses a convergent subsequence (which denoted by
possesses a convergent subsequence (which denoted by  ), and then there exists a vector
), and then there exists a vector  such that
such that

Without loss of generality, we assume that  . Since
. Since  , there exist
, there exist  such that
such that

and then from (3.27) we have

Since  (as
(as  ),
),  and
and  , we have
, we have

From (3.28)–(3.32), we have

So we get

where  satisfies
satisfies 
Since  from(1.2) and (3.34), we have
from(1.2) and (3.34), we have

Since  , according to the continuity of
, according to the continuity of  we have
we have

and it is a contradiction to (3.35). This implies that there exists a big enough  such that all the solutions of (3.21) with (1.2) belong to
such that all the solutions of (3.21) with (1.2) belong to  , and then we have
, and then we have

If we prove that  , then we obtain the existence of solutions (3.18) with (1.2).
, then we obtain the existence of solutions (3.18) with (1.2).
Now we consider the following equation with: (1.2)

where 
We denote  defined by
defined by

Similar to the proof of Theorem 3.1, we know that (3.38) with (1.2) has the same solution of

Similar to the discussions of the above, for any  all the solutions of (3.38) with (1.2) are uniformly bounded.
all the solutions of (3.38) with (1.2) are uniformly bounded.
If  is a solution of the following equation with (1.2):
is a solution of the following equation with (1.2):

then we have

Since  we have
we have  and it means that
and it means that  is a solution of
is a solution of

according to hypothesis (30), (3.38) has no solutions  on
on  then we get that for each
then we get that for each  , the Leray-Schauder degree
, the Leray-Schauder degree  is well defined, and from the properties of that degree, we have
is well defined, and from the properties of that degree, we have

Now it is clear that  So
So  If we prove that
If we prove that  , then we obtain the existence of solutions (3.18) with (1.2). By the properties of the Leray-Schauder degree, we have
, then we obtain the existence of solutions (3.18) with (1.2). By the properties of the Leray-Schauder degree, we have

By hypothesis (40), this last degree is different from zero. We obtain that (3.18) with (1.2) has at least one solution. This completes the proof.
Corollary 3.3.
If  is Caratheodory, which satisfies the conditions of Theorem 3.2,
is Caratheodory, which satisfies the conditions of Theorem 3.2,  where
where  are positive functions, and satisfies
are positive functions, and satisfies  then (3.18) with (1.2) has at least one solution.
then (3.18) with (1.2) has at least one solution.
Proof.
Since

then  has only one solution
has only one solution  , and
, and

and according to Theorem 3.2, we get that (3.18) with (1.2) has at least a solution. This completes the proof.
Now let us consider the boundary asymptotic behavior of solutions of system (1.1)-(1.2).
Theorem 3.4.
If  is a solution of (1.1)-(1.2) which is given in Theorem 3.2, then
is a solution of (1.1)-(1.2) which is given in Theorem 3.2, then
(i)
(ii) as
as 
(iii) as
as 
Proof.
Since  exists and
exists and  ,
,  and
and  both exist and equal, we can conclude that
both exist and equal, we can conclude that  . Since
. Since  we have
we have  Thus
Thus
(i)
(ii) as
as
(iii) as
as
This completes the proof.
Corollary 3.5.
Assume that  exists,
exists,  , and
, and

then
(i)
(ii) as
as 
(iii) as
as 
4. 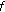 Satisfies General Growth Condition
Satisfies General Growth Condition
In this section, under the condition that  satisfies
satisfies

where  are nonnegative,
are nonnegative,  ,
,  and
and  almost every in
almost every in  we will apply Leray-Schauder's degree to deal with the existence of solutions for (1.1) with boundary value problems. Moreover the asymptotic behavior has been discussed.
we will apply Leray-Schauder's degree to deal with the existence of solutions for (1.1) with boundary value problems. Moreover the asymptotic behavior has been discussed.
Throughout the paper, assume that
(A1) are nonnegative and satisfying
are nonnegative and satisfying  or
or  ;
;
(A2) ;
;  ;
;  keeps sign on
keeps sign on  , and satisfies
, and satisfies

where  and
and  are positive constants.
are positive constants.
For any  , without loss of generality, we may denote
, without loss of generality, we may denote  . Denote
. Denote  . According to (A1), then there exists a positive constant
. According to (A1), then there exists a positive constant  that satisfies
that satisfies

We also assume the following
(A3) satisfies
satisfies

(A4) satisfies
satisfies

Note.
Let  , and (A
, and (A )-(A
)-(A ) are satisfied. If
) are satisfied. If  and
and  are positive small enough, then it is easy to see that (A
are positive small enough, then it is easy to see that (A )-(A
)-(A ) are satisfied.
) are satisfied.
Denote

It is easy to see that  is an open bounded domain in
is an open bounded domain in  .
.
Theorem 4.1.
If  satisfies (4.1), and (A1)–(A4) are satisfied, then the system (1.1)-(1.2) has a solution on
satisfies (4.1), and (A1)–(A4) are satisfied, then the system (1.1)-(1.2) has a solution on  .
.
Proof.
We only need to prove that the conditions of Theorem 3.1 are satisfied.
(10) We only need to prove that for each  the problem
the problem

with boundary condition (1.2) has no solution on  .
.
If it is false, then there exists a  and
and  is a solution of (4.7) with (1.2).
is a solution of (4.7) with (1.2).
Since  , there exists an
, there exists an  such that
such that  .
.
-
(i)
Suppose that
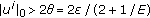 , then
, then 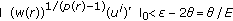 . Since
. Since  , there exists
, there exists 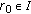 such that
such that  . For any
. For any  , we have
, we have

This implies that  for each
for each  . Since
. Since  ,
,  keeps sign. Since
keeps sign. Since  keeps sign,
keeps sign,  also keeps sign.
also keeps sign.
Assume that  is positive, then
is positive, then

It is a contradiction to (1.2).
Assume that  is negative, then
is negative, then

It is a contradiction to (1.2).
-
(ii)
Suppose that
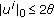 , then
, then 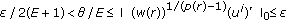 .
.
This implies that  for some
for some  . Since
. Since  , it is easy to see that
, it is easy to see that

According to the boundary value condition, there exists a  such that
such that

then

Since  , combining (4.11), we have
, combining (4.11), we have

It is a contradiction.
Summarizing this argument, for each  the problem (4.7) with (1.2) has no solution on
the problem (4.7) with (1.2) has no solution on  .
.
(20) For any  , without loss of generality, we may assume that
, without loss of generality, we may assume that  and
and  , then we have
, then we have

It means that  has no solution on
has no solution on  .
.
(30) Let

Denote

According to (A ), it is easy to see that, for any
), it is easy to see that, for any  ,
,  does not have solution on
does not have solution on  , then the Brouwer degree
, then the Brouwer degree

This completes the proof.
Theorem 4.2.
If  is a solution of (1.1)-(1.2) which is given in Theorem 4.1, then
is a solution of (1.1)-(1.2) which is given in Theorem 4.1, then
(i)
(ii) as
as 
(iii) as
as 
Proof.
Since  exists and
exists and  and
and  both exist and equal, we have
both exist and equal, we have  Thus
Thus
(i)
(ii) as
as 
(iii) as
as 
We completes the proof.
Corollary 4.3.
Assume that  exists,
exists,  , and
, and 

then
(i)
(ii) as
as 
(iii) as
as  .
.
Similar to the proof of Theorem 4.1, we have the following.
Theorem 4.4.
Assume that  , where
, where  satisfy
satisfy  . On the conditions of (A1)–(A4), if
. On the conditions of (A1)–(A4), if  , then problem (1.1)-(1.2) possesses at least one solution.
, then problem (1.1)-(1.2) possesses at least one solution.
On the typical case, we have the following.
Corollary 4.5.
Assume that  , where
, where  satisfy
satisfy  . On the conditions of Theorem 4.1, then problem (1.1)-(1.2) possesses at least one solution.
. On the conditions of Theorem 4.1, then problem (1.1)-(1.2) possesses at least one solution.
References
Acerbi E, Mingione G: Regularity results for a class of functionals with non-standard growth. Archive for Rational Mechanics and Analysis 2001,156(2):121–140. 10.1007/s002050100117
Chen Y, Levine S, Rao M: Variable exponent, linear growth functionals in image restoration. SIAM Journal on Applied Mathematics 2006,66(4):1383–1406. 10.1137/050624522
Diening L: Maximal function on generalized Lebesgue spaces . Mathematical Inequalities & Applications 2004,7(2):245–253.
Fan X-L, Zhang Q-H: Existence of solutions for -Laplacian Dirichlet problem. Nonlinear Analysis: Theory, Methods & Applications 2003,52(8):1843–1852. 10.1016/S0362-546X(02)00150-5
Fan X-L, Wu H-Q, Wang F-Z: Hartman-type results for -Laplacian systems. Nonlinear Analysis: Theory, Methods & Applications 2003,52(2):585–594. 10.1016/S0362-546X(02)00124-4
Fan X, Zhang Q, Zhao D: Eigenvalues of -Laplacian Dirichlet problem. Journal of Mathematical Analysis and Applications 2005,302(2):306–317. 10.1016/j.jmaa.2003.11.020
El Hamidi A: Existence results to elliptic systems with nonstandard growth conditions. Journal of Mathematical Analysis and Applications 2004,300(1):30–42. 10.1016/j.jmaa.2004.05.041
Hudzik H: On generalized Orlicz-Sobolev space. Functiones et Approximatio Commentarii Mathematici 1976, 4: 37–51.
Kováčik O, Rákosník J: On spaces and . Czechoslovak Mathematical Journal 1991,41(4):592–618.
Zhang Q: Existence of positive solutions for elliptic systems with nonstandard -growth conditions via sub-supersolution method. Nonlinear Analysis: Theory, Methods & Applications 2007,67(4):1055–1067. 10.1016/j.na.2006.06.017
Zhang Q: Existence of positive solutions for a class of -Laplacian systems. Journal of Mathematical Analysis and Applications 2007,333(2):591–603. 10.1016/j.jmaa.2006.11.037
Zhang Q: Existence of solutions for weighted -Laplacian system boundary value problems. Journal of Mathematical Analysis and Applications 2007,327(1):127–141. 10.1016/j.jmaa.2006.03.087
Zhang Q, Qiu Z, Liu X: Existence of solutions for a class of weighted -Laplacian system multipoint boundary value problems. Journal of Inequalities and Applications 2008, 2008:-18.
Zhang Q, Liu X, Qiu Z: The method of subsuper solutions for weighted -Laplacian equation boundary value problems. Journal of Inequalities and Applications 2008, 2008:-19.
Zhang Q: Boundary blow-up solutions to -Laplacian equations with exponential nonlinearities. Journal of Inequalities and Applications 2008, 2008:-8.
Růžička M: Electrorheological Fluids: Modeling and Mathematical Theory, Lecture Notes in Mathematics. Volume 1748. Springer, Berlin, Germany; 2000:xvi+176.
Zhikov VV: Averaging of functionals of the calculus of variations and elasticity theory. Izvestiya Akademii Nauk SSSR. Seriya Matematicheskaya 1987,29(1):33–66.
Guo Y, Shan W, Ge W: Positive solutions for second-order -point boundary value problems. Journal of Computational and Applied Mathematics 2003,151(2):415–424. 10.1016/S0377-0427(02)00739-2
Wang Y, Ge W: Existence of multiple positive solutions for multipoint boundary value problems with a one-dimensional -Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2007,67(2):476–485. 10.1016/j.na.2006.06.011
Wang Y, Ge W: Multiple positive solutions for multipoint boundary value problems with one-dimensional -Laplacian. Journal of Mathematical Analysis and Applications 2007,327(2):1381–1395. 10.1016/j.jmaa.2006.05.023
Wang Y, Ge W: Positive solutions for multipoint boundary value problems with a one-dimensional -Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2007,66(6):1246–1256. 10.1016/j.na.2006.01.015
Acknowlegments
This work is partly supported by the National Science Foundation of China (10701066 and 10671084) and China Postdoctoral Science Foundation (20070421107), the Natural Science Foundation of Henan Education Committee (2008-755-65), and the Natural Science Foundation of Jiangsu Education Committee (08KJD110007).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Qiu, Z., Zhang, Q. & Wang, Y. Existence and Asymptotic Behavior of Solutions for Weighted  -Laplacian System Multipoint Boundary Value Problems in Half Line.
J Inequal Appl 2009, 926518 (2009). https://doi.org/10.1155/2009/926518
-Laplacian System Multipoint Boundary Value Problems in Half Line.
J Inequal Appl 2009, 926518 (2009). https://doi.org/10.1155/2009/926518
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/926518
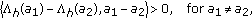
 sends bounded sets to bounded sets, and
sends bounded sets to bounded sets, and 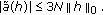
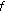 Satisfies Sub-(
Satisfies Sub-(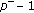 ) Growth Condition
) Growth Condition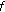 Satisfies General Growth Condition
Satisfies General Growth Condition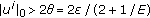 , then
, then 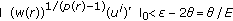 . Since
. Since  , there exists
, there exists 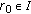 such that
such that  . For any
. For any  , we have
, we have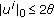 , then
, then 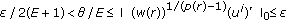 .
.