- Research Article
- Open access
- Published:
Optimality Conditions of Globally Efficient Solution for Vector Equilibrium Problems with Generalized Convexity
Journal of Inequalities and Applications volume 2009, Article number: 898213 (2009)
Abstract
We study optimality conditions of globally efficient solution for vector equilibrium problems with generalized convexity. The necessary and sufficient conditions of globally efficient solution for the vector equilibrium problems are obtained. The Kuhn-Tucker condition of globally efficient solution for vector equilibrium problems is derived. Meanwhile, we obtain the optimality conditions for vector optimization problems and vector variational inequality problems with constraints.
1. Introduction
Throughout the paper, let  ,
,  and
and  be real Hausdorff topological vector spaces,
be real Hausdorff topological vector spaces,  a nonempty subset, and
a nonempty subset, and  denotes the zero element of
denotes the zero element of  . Let
. Let  and
and  be two pointed convex cones (see [1]) such that
be two pointed convex cones (see [1]) such that  ,
,  , where
, where  denotes the interior of
denotes the interior of  . Let
. Let  be a mapping and let
be a mapping and let  be a mapping such that
be a mapping such that  , for all
, for all  . For each
. For each  , we denote
, we denote  and define the constraint set
and define the constraint set

which is assumed to be nonempty.
Consider the vector equilibrium problems with constraints (for short, VEPC): finding  such that
such that

where  is a convex cone in
is a convex cone in  .
.
Vector equilibrium problems, which contain vector optimization problems, vector variational inequality problems, and vector complementarity problems as special case, have been studied by Ansari et al. [2, 3], Bianchi et al. [4], Fu [5], Gong [6], Gong and Yao [7, 8], Hadjisavvas and Schaible [9], Kimura and Yao [10–13], Oettli [14], and Zeng et al. [15]. But so far, most papers focused mainly on the existence of solutions and the properties of the solutions, there are few papers which deal with the optimality conditions. Giannessi et al. [16] turned the vector variational inequalities with constraints into another vector variational inequalities without constraints. They gave sufficient conditions for efficient solution and weakly efficient solution of the vector variational inequalities in finite dimensional spaces. Morgan and Romaniello [17] gave scalarization and Kuhn-Tucker-like conditions for weak vector generalized quasivariational inequalities in Hilbert space by using the concept of subdifferential of the function. Gong [18] presented the necessary and sufficient conditions for weakly efficient solution, Henig efficient solution, and superefficient solution for the vector equilibrium problems with constraints under the condition of cone-convexity. However, the condition of cone-convexity is too strong. Some generalized convexity has been developed, such as cone-preinvexity (see [19]), cone-convexlikeness (see [20]), cone-subconvexlikeness (see [21]), and generalized cone-convexlikeness (see [22]). Among them, the generalized cone-subconvexlikeness has received more attention. Then, it is important to give the optimality conditions for the solution of (VEPC) under conditions of generalized convexity. Moreover, it appears that no work has been done on the Kuhn-Tucker condition of solution for (VEPC). This paper is the effort in this direction.
In the paper, we study the optimality conditions for the vector equilibrium problems. Firstly, we present the necessary and sufficient conditions for globally efficient solution of (VEPC) under generalized cone-subconvexlikeness. Secondly, we prove that the Kuhn-Tucker condition for (VEPC) is both necessary and sufficient under the condition of cone-preinvexity. Meanwhile, we obtain the optimality conditions for vector optimization problems with constraints and vector variational inequality problems with constraints in Section 4.
2. Preliminaries and Definitions
Let  ,
,  be the dual space of
be the dual space of  ,
,  , respectively, then the dual cone of
, respectively, then the dual cone of  is defined as
is defined as

The set of strictly positive functional in  is denoted by
is denoted by  , that is,
, that is,

It is well known that
(i)if  , then
, then  has a base;
has a base;
(ii)if  is a Hausdorff locally convex space, then
is a Hausdorff locally convex space, then  if and only if
if and only if  has a base;
has a base;
(iii)if  is a separable normed space and
is a separable normed space and  is a pointed closed convex cone, then
is a pointed closed convex cone, then  is nonempty (see [1]).
is nonempty (see [1]).
Remark 2.1.
The positive cone in many common Banach spaces possesses strictly positive functionals. However, this is not always the case (see [23]).
Let  be an arbitrary nonempty subset and
be an arbitrary nonempty subset and  . The symbol
. The symbol  denotes the closure of
denotes the closure of  , and
, and  denotes the generated cone of
denotes the generated cone of  , that is,
, that is,  . When
. When  is a convex, so is
is a convex, so is  .
.
Remark 2.2.
Obviously, we have
(i) ;
;
(ii) ;
;
(iii)if  satisfying for all
satisfying for all  ,
,  , then
, then  .
.
Several definitions of generalized convex mapping have been introduced in literature.
(1)Let  be a nonempty convex subset and let
be a nonempty convex subset and let  be a convex cone. A mapping
be a convex cone. A mapping  is called
is called  -convex, if for all
-convex, if for all  , for all
, for all  , we have
, we have

(2)Let  be a nonempty subset and let
be a nonempty subset and let  be a convex cone.
be a convex cone.
(i)A mapping  is called
is called  -convexlike (see [20]), if for all
-convexlike (see [20]), if for all  , for all
, for all  , there exists
, there exists  such that
such that

(ii) is said to be
is said to be  -subconvexlike (see [21]), if there exists
-subconvexlike (see [21]), if there exists  such that for all
such that for all  , for all
, for all  , for all
, for all  , there exists
, there exists  such that
such that

(iii) is said to be generalized
is said to be generalized  -subconvexlike (see [22]), if there exists
-subconvexlike (see [22]), if there exists  such that for all
such that for all  , for all
, for all  , for all
, for all  , there exists
, there exists  ,
,  such that
such that

A nonempty subset  is called invex with respect to
is called invex with respect to  , if there exists a mapping
, if there exists a mapping  such that for any
such that for any  , and
, and  ,
,  .
.
(3)Let  be a invex set with respect to
be a invex set with respect to  . A mapping
. A mapping  is said to be
is said to be  -preinvex with respect to
-preinvex with respect to  (see [19]), if for any
(see [19]), if for any  , and
, and  , we have
, we have

Remark 2.3.
-
(i)
From [21], we know that
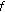 is
is 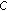 -convexlike on
-convexlike on 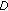 if and only if
if and only if  is a convex set and
is a convex set and 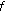 is
is 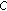 -subconvexlike on
-subconvexlike on  if and only if
if and only if 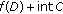 is a convex set.
is a convex set. -
(ii)
If
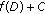 is a convex set, so is
is a convex set, so is 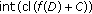 . By Lemma
. By Lemma 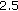 of [24],
of [24], 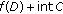 is convex. This shows that
is convex. This shows that  -convexlikeness implies
-convexlikeness implies 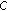 -subconvexlikeness. But in general the converse is not true (see [21]).
-subconvexlikeness. But in general the converse is not true (see [21]). -
(iii)
It is clear that
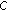 -subconvexlikeness implies generalized
-subconvexlikeness implies generalized 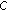 -subconvexlikeness. But in general the converse is not true (see [22]).
-subconvexlikeness. But in general the converse is not true (see [22]).
Remark 2.4.
For  , the invex set is a convex set and the
, the invex set is a convex set and the  -preinvex mapping is a convex mapping. However, there are mappings which are
-preinvex mapping is a convex mapping. However, there are mappings which are  -preinvex but not convex (see [25]).
-preinvex but not convex (see [25]).
Relationships among various types of convexity are as shown below:

Yang [26] proved the following Lemma in Banach space; Chen and Rong [27] generalized the result to topological vector space.
Lemma 2.5.
Assume that  . Then
. Then  is generalized
is generalized  -subconvexlike if and only if
-subconvexlike if and only if  is convex.
is convex.
Lemma 2.6.
Assume that (i)  is a nonempty subset and
is a nonempty subset and  is a convex cone with
is a convex cone with  . (ii)
. (ii)  is convex. Then
is convex. Then  is also convex.
is also convex.
Proof.
By Lemma 2.5 and Remark 2.1(iii), we deduce that  is a convex set. It is not difficult to prove that
is a convex set. It is not difficult to prove that  is a convex set.
is a convex set.
Note that  and the closure of a convex set is convex, then
and the closure of a convex set is convex, then  is a convex set. The proof is finished.
is a convex set. The proof is finished.
Lemma 2.7 (see [1]).
If  ,
,  , then
, then  .
.
Assume that  , a vector
, a vector  is called a weakly efficient solution of (VEPC), if
is called a weakly efficient solution of (VEPC), if  satisfies
satisfies

Definition 2.8 (see [6]).
Let  be a convex cone. Also,
be a convex cone. Also,  is said to be a globally efficient solution of (VEPC), if there exists a pointed convex cone
is said to be a globally efficient solution of (VEPC), if there exists a pointed convex cone  with
with  such that
such that

Remark 2.9.
Obviously,  is a globally efficient solution of (VEPC), then
is a globally efficient solution of (VEPC), then  is also a weakly efficient solution of (VEPC). But in general the converse is not true (see [6]).
is also a weakly efficient solution of (VEPC). But in general the converse is not true (see [6]).
3. Optimality Conditions
Theorem 3.1.
Assume that (i)  and there exists
and there exists  such that
such that  ; (ii)
; (ii)  is a generalized
is a generalized  -subconvexlike on
-subconvexlike on  . Then
. Then  is a globally efficient solution of (VEPC) if and only if there exists
is a globally efficient solution of (VEPC) if and only if there exists  and
and  such that
such that


Proof.
Assume that  is a globally efficient solution of (VEPC), then there exists a pointed convex cone
is a globally efficient solution of (VEPC), then there exists a pointed convex cone  with
with  such that
such that

Since  is a pointed convex cone with
is a pointed convex cone with  , then
, then

Note that  , for all
, for all  and above formula, it is not difficult to prove
and above formula, it is not difficult to prove

Since  and
and  are two open sets and
are two open sets and  are two pointed convex cones, by (3.5), we have
are two pointed convex cones, by (3.5), we have

Moreover, since  is a generalized
is a generalized  -subconvexlike on
-subconvexlike on  , by Lemma 2.5,
, by Lemma 2.5,  is convex. This follows from Lemma 2.6 that
is convex. This follows from Lemma 2.6 that  is convex. By the standard separation theorem (see [1, page 76]), there exists
is convex. By the standard separation theorem (see [1, page 76]), there exists  such that
such that

Since  is a cone, it follows from (3.7) that
is a cone, it follows from (3.7) that

Note that  , thus
, thus  . By (3.8), we obtain immediately
. By (3.8), we obtain immediately

It implies that

On the other hand, by  and (3.7), we get
and (3.7), we get

Since for all  , for all
, for all  , we have
, we have  , by (3.11), we get
, by (3.11), we get

Letting  , we have
, we have

Firstly, we prove that

Since  is convex and
is convex and  is nonempty, then
is nonempty, then  . Note that
. Note that  and (3.13), and we have
and (3.13), and we have  . With similar proof of
. With similar proof of  , we can prove that
, we can prove that  .
.
We need to show that  .
.
In fact, if  , then
, then  . By (3.10), we have
. By (3.10), we have

On the other hand, since  ,
,  , by Lemma 2.7, we have
, by Lemma 2.7, we have  , which is a contradiction with (3.15).
, which is a contradiction with (3.15).
Secondly, we show that  .
.
For any  , since
, since  , then there exists a balanced neighborhood
, then there exists a balanced neighborhood  of zero element such that
of zero element such that

Note that  , and there exists
, and there exists  such that
such that 
Since  , then
, then

By the arbitrariness of  , we have
, we have  .
.
Lastly, we show that (3.1) and (3.2) hold.
Taking  in (3.10), we get
in (3.10), we get

Moreover, since  , then
, then

Thus (3.2) holds.
Since  and
and  , by (3.10), we have
, by (3.10), we have

Then (3.1) holds.
Conversely, if  is not a globally efficient solution of (VEPC), then for any pointed convex cone
is not a globally efficient solution of (VEPC), then for any pointed convex cone  with
with  , we have
, we have

By  , let
, let

Obviously,  is a pointed convex cone and
is a pointed convex cone and  . By (3.21), then there exists
. By (3.21), then there exists  such that
such that

By the definition of  , we get
, we get

Moreover, since  and
and  , then
, then

This together with (3.24) implies that

On the other hand, since  , by (3.1) and (3.2), we get
, by (3.1) and (3.2), we get

which contradicts (3.26). The proof is finished.
Corollary 3.2.
Assume that (i)  is invex with respect to
is invex with respect to  ; (ii)
; (ii)  and there exists
and there exists  such that
such that  ; (iii)
; (iii)  is
is  -preinvex on
-preinvex on  with respect to
with respect to  , and
, and  is
is  -preinvex on
-preinvex on  with respect to
with respect to  . Then
. Then  is a globally efficient solution of (VEPC) if and only if there exist
is a globally efficient solution of (VEPC) if and only if there exist  and
and  such that (3.1) and (3.2) hold.
such that (3.1) and (3.2) hold.
Proof.
Since  is
is  -preinvex on
-preinvex on  with respect to
with respect to  is
is  -preinvex on
-preinvex on  with respect to
with respect to  . Then
. Then  is
is  -preinvex on
-preinvex on  with respect to
with respect to  . Thus by Theorem 3.1, the conclusion of Corollary 3.2 holds.
. Thus by Theorem 3.1, the conclusion of Corollary 3.2 holds.
Remark 3.3.
Corollary 3.2 generalizes and improves the recent results of Gong (see [18, Theorem 3.3]). Especially, Corollary 3.2 generalizes and improves in the following several aspects.
(1)The condition that the subset  is convex is extended to invex.
is convex is extended to invex.
(2) is
is  -convex in
-convex in  is extended to
is extended to  -preinvex in
-preinvex in 
(3) is
is  -convex is extended to
-convex is extended to  -preinvex.
-preinvex.
Next, we introduce Gateaux derivative of mapping.
Let  and let
and let  be a mapping.
be a mapping.  is called Gateaux differentiable at
is called Gateaux differentiable at  if for any
if for any  , there exists limit
, there exists limit

Mapping  is called Gateaux derivative of
is called Gateaux derivative of  at
at  .
.
The following theorem shows that the Kuhn-Tucker condition for (VEPC) is both necessary and sufficient.
Theorem 3.4.
Assume that (i)  ,
,  are closed,
are closed,  is invex with respect to
is invex with respect to  ; (ii)
; (ii)  and there exists
and there exists  such that
such that  ; (iii)
; (iii)  is
is  -preinvex on
-preinvex on  with respect to
with respect to  and Gateaux differentiable at
and Gateaux differentiable at  , and
, and  is Gateaux differentiable at
is Gateaux differentiable at  and
and  -preinvex on
-preinvex on  with respect to
with respect to  ; . Then
; . Then  is a globally efficient solution of (VEPC) if and only if there exists
is a globally efficient solution of (VEPC) if and only if there exists  and
and  such that
such that


Proof.
Assume that  is a globally efficient solution of (VEPC), by Corollary 3.2, there exists
is a globally efficient solution of (VEPC), by Corollary 3.2, there exists  and
and  such that
such that


Since  is invex with respect to
is invex with respect to  , then for any
, then for any  ,
,

By (3.32), for any  , we have
, we have

Since  is Gateaux differentiable at
is Gateaux differentiable at  , and
, and  is Gateaux differentiable at
is Gateaux differentiable at  , letting
, letting  in (3.34), we have
in (3.34), we have

Conversely, if  is not a globally efficient solution of (VEPC), a similar proof of (3.24) in Theorem 3.1, there exists
is not a globally efficient solution of (VEPC), a similar proof of (3.24) in Theorem 3.1, there exists  such that
such that

Since  , thus we have
, thus we have

Moreover, since  is
is  -preinvex on
-preinvex on  with respect to
with respect to  , then for any
, then for any  ,
,  , we have
, we have

This together with  being cone yields that
being cone yields that

Since  is closed, taking
is closed, taking  in the above formula, we have
in the above formula, we have

Note that  , then we have
, then we have

This together with (3.37) yields that

Moreover, since  ,
,  and
and  , then we have
, then we have

With similar proof of (3.41), we get

This together with (3.42) implies that

which contradicts (3.29). The proof is finished.
4. Application
As interesting applications of the results of Section 3, we obtain the optimality conditions for vector optimization problems and vector variational inequality problems.
Let  be the space of all bounded linear mapping from
be the space of all bounded linear mapping from  to
to  . We denote by
. We denote by  the value of
the value of  at
at  .
.
Equation (VEPC) includes as a special case a vector variational inequality with constraints (for short, (VVIC)) involving

where  is a mapping from
is a mapping from  to
to  .
.
Definition 4.1 (see [18]).
If  ,
,  , and if
, and if  is a globally efficient solution of (VEPC), then
is a globally efficient solution of (VEPC), then  is called a globally efficient solution of (VVIC).
is called a globally efficient solution of (VVIC).
Theorem 4.2.
Assume that (i)  ,
,  are closed,
are closed,  is a nonempty convex subset; (ii)
is a nonempty convex subset; (ii)  and there exists
and there exists  such that
such that  ; (iii)
; (iii)  is Gateaux differentiable at
is Gateaux differentiable at  and
and  -convex on
-convex on  . Then
. Then  is a globally efficient solution of (VVIC) if and only if there exists
is a globally efficient solution of (VVIC) if and only if there exists  and
and  such that
such that

Proof.
Let

then  is invex with respect to
is invex with respect to 
 is Gateaux differentiable at
is Gateaux differentiable at  and
and  -preinvex with respect to
-preinvex with respect to  , and
, and  is Gateaux differentiable at
is Gateaux differentiable at  and
and  -preinvex on
-preinvex on  with respect to
with respect to  . Thus the conditions of Theorem 3.4 are satisfied. Note that
. Thus the conditions of Theorem 3.4 are satisfied. Note that  , by Theorem 3.4, then the conclusion of Theorem 4.2 holds.
, by Theorem 3.4, then the conclusion of Theorem 4.2 holds.
Another special case of (VEPC) is the vector optimization problem with constraints (for short, VOP):

involving

where  is a mapping.
is a mapping.
Definition 4.3 (see [18]).
If  ,
,  , and if
, and if  is a globally efficient solution of (VEPC), then
is a globally efficient solution of (VEPC), then  is called a globally efficient solution of (VOP).
is called a globally efficient solution of (VOP).
Theorem 4.4.
Assume that (i)  ,
,  are closed,
are closed,  is invex with respect to
is invex with respect to  ; (ii)
; (ii)  and there exists
and there exists  such that
such that  ; (iii)
; (iii)  is Gateaux differentiable at
is Gateaux differentiable at  and
and  -preinvex on
-preinvex on  with respect to
with respect to  , and
, and  is Gateaux differentiable at
is Gateaux differentiable at  and
and  -preinvex on
-preinvex on  with respect to
with respect to  . Then
. Then  is a globally efficient solution of (VOP) if and only if there exists
is a globally efficient solution of (VOP) if and only if there exists  and
and  such that
such that

Proof.
Let

then  is Gateaux differentiable at
is Gateaux differentiable at  and
and  -preinvex with respect to
-preinvex with respect to  , and
, and  is Gateaux differentiable at
is Gateaux differentiable at  and
and  -preinvex on
-preinvex on  with respect to
with respect to  . Thus the conditions of Theorem 3.4 are satisfied. Note that
. Thus the conditions of Theorem 3.4 are satisfied. Note that  , by Theorem 3.4, then the conclusion of Theorem 4.4 holds.
, by Theorem 3.4, then the conclusion of Theorem 4.4 holds.
By Theorem 3.1, we have the following result.
Theorem 4.5.
Assume that (i)  and there exists
and there exists  such that
such that  ; (ii)
; (ii)  is generalized
is generalized  -subconvexlike on
-subconvexlike on  . Then
. Then  is a globally efficient solution of (VOP) if and only if there exists
is a globally efficient solution of (VOP) if and only if there exists  and
and  such that
such that

References
Jahn J: Mathematical Vector Optimization in Partially Ordered Linear Spaces, Methods and Procedures in Mathematical Physics. Volume 31. Peter D. Lang, Frankfurt, Germany; 1986:viii+310.
Ansari QH, Oettli W, Schläger D: A generalization of vectorial equilibria. Mathematical Methods of Operations Research 1997,46(2):147–152. 10.1007/BF01217687
Ansari QH, Konnov IV, Yao JC: Characterizations of solutions for vector equilibrium problems. Journal of Optimization Theory and Applications 2002,113(3):435–447. 10.1023/A:1015366419163
Bianchi M, Hadjisavvas N, Schaible S: Vector equilibrium problems with generalized monotone bifunctions. Journal of Optimization Theory and Applications 1997,92(3):527–542. 10.1023/A:1022603406244
Fu J: Simultaneous vector variational inequalities and vector implicit complementarity problem. Journal of Optimization Theory and Applications 1997,93(1):141–151. 10.1023/A:1022653918733
Gong X-H: Connectedness of the solution sets and scalarization for vector equilibrium problems. Journal of Optimization Theory and Applications 2007,133(2):151–161. 10.1007/s10957-007-9196-y
Gong X-H, Yao JC: Connectedness of the set of efficient solutions for generalized systems. Journal of Optimization Theory and Applications 2008,138(2):189–196. 10.1007/s10957-008-9378-2
Gong X-H, Yao JC: Lower semicontinuity of the set of efficient solutions for generalized systems. Journal of Optimization Theory and Applications 2008,138(2):197–205. 10.1007/s10957-008-9379-1
Hadjisavvas N, Schaible S: From scalar to vector equilibrium problems in the quasimonotone case. Journal of Optimization Theory and Applications 1998,96(2):297–309. 10.1023/A:1022666014055
Kimura K, Yao J-C: Semicontinuity of solution mappings of parametric generalized strong vector equilibrium problems. Journal of Industrial and Management Optimization 2008,4(1):167–181.
Kimura K, Yao J-C: Sensitivity analysis of solution mappings of parametric vector quasi-equilibrium problems. Journal of Global Optimization 2008,41(2):187–202. 10.1007/s10898-007-9210-9
Kimura K, Yao J-C: Sensitivity analysis of solution mappings of parametric generalized quasi vector equilibrium problems. Taiwanese Journal of Mathematics 2008,12(9):2233–2268.
Kimura K, Yao J-C: Sensitivity analysis of vector equilibrium problems. Taiwanese Journal of Mathematics 2008,12(3):649–669.
Oettli W: A remark on vector-valued equilibria and generalized monotonicity. Acta Mathematica Vietnamica 1997,22(1):213–221.
Zeng L-C, Wu S-Y, Yao J-C: Generalized KKM theorem with applications to generalized minimax inequalities and generalized equilibrium problems. Taiwanese Journal of Mathematics 2006,10(6):1497–1514.
Giannessi F, Mastroeni G, Pellegrini L: On the theory of vector optimization and variational inequalities. Image space analysis and separation. In Vector Variational Inequalities and Vector Equilibria: Mathematical Theories, Nonconvex Optimization and Its Applications. Volume 38. Edited by: Giannessi F. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2000:153–215.
Morgan J, Romaniello M: Scalarization and Kuhn-Tucker-like conditions for weak vector generalized quasivariational inequalities. Journal of Optimization Theory and Applications 2006,130(2):309–316. 10.1007/s10957-006-9104-x
Gong X-H: Optimality conditions for vector equilibrium problems. Journal of Mathematical Analysis and Applications 2008,342(2):1455–1466. 10.1016/j.jmaa.2008.01.026
Ben-Israel A, Mond B: What is invexity? Journal of the Australian Mathematical Society. Series B 1986,28(1):1–9. 10.1017/S0334270000005142
Hayashi M, Komiya H: Perfect duality for convexlike programs. Journal of Optimization Theory and Applications 1982,38(2):179–189. 10.1007/BF00934081
Jeyakumar V: A generalization of a minimax theorem of Fan via a theorem of the alternative. Journal of Optimization Theory and Applications 1986,48(3):525–533. 10.1007/BF00940575
Yang XM: Alternative theorems and optimality conditions with weakened convexity. Opsearch 1992, 29: 125–135.
Truong XDH: Cones admitting strictly positive functionals and scalarization of some vector optimization problems. Journal of Optimization Theory and Applications 1997,93(2):355–372. 10.1023/A:1022654107386
Breckner WW, Kassay G: A systematization of convexity concepts for sets and functions. Journal of Convex Analysis 1997,4(1):109–127.
Weir T, Jeyakumar V: A class of nonconvex functions and mathematical programming. Bulletin of the Australian Mathematical Society 1988,38(2):177–189. 10.1017/S0004972700027441
Yang XM: Generalized subconvexlike functions and multiple objective optimization. Systems Science and Mathematical Sciences 1995,8(3):254–259.
Chen GY, Rong WD: Characterizations of the Benson proper efficiency for nonconvex vector optimization. Journal of Optimization Theory and Applications 1998,98(2):365–384. 10.1023/A:1022689517921
Acknowledgment
This work was supported by the National Natural Science Foundation of China (no. 10771228).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Qiu, Q. Optimality Conditions of Globally Efficient Solution for Vector Equilibrium Problems with Generalized Convexity. J Inequal Appl 2009, 898213 (2009). https://doi.org/10.1155/2009/898213
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/898213
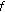 is
is 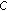 -convexlike on
-convexlike on 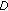 if and only if
if and only if  is a convex set and
is a convex set and 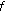 is
is 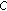 -subconvexlike on
-subconvexlike on  if and only if
if and only if 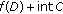 is a convex set.
is a convex set.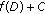 is a convex set, so is
is a convex set, so is 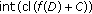 . By Lemma
. By Lemma 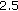 of [
of [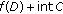 is convex. This shows that
is convex. This shows that  -convexlikeness implies
-convexlikeness implies 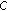 -subconvexlikeness. But in general the converse is not true (see [
-subconvexlikeness. But in general the converse is not true (see [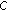 -subconvexlikeness implies generalized
-subconvexlikeness implies generalized 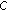 -subconvexlikeness. But in general the converse is not true (see [
-subconvexlikeness. But in general the converse is not true (see [