- Research Article
- Open access
- Published:
New Results on the Nonoscillation of Solutions of Some Nonlinear Differential Equations of Third Order
Journal of Inequalities and Applications volume 2009, Article number: 896934 (2009)
Abstract
We give sufficient conditions so that all solutions of differential equations  , and
, and  , are nonoscillatory. Depending on these criteria, some results which exist in the relevant literature are generalized. Furthermore, the conditions given for the functions
, are nonoscillatory. Depending on these criteria, some results which exist in the relevant literature are generalized. Furthermore, the conditions given for the functions  and
and  lead to studying more general differential equations.
lead to studying more general differential equations.
1. Introduction
This paper is concerned with study of nonoscillation of solutions of third-order nonlinear differential equations of the form


where  is a fixed real number,
is a fixed real number,  ,
,  ,
,  ,
,  , and
, and  such that
such that  and
and  for all
for all  .
.  are nondecreasing such that
are nondecreasing such that  ,
,  for all
for all  ,
,  . Throughout the paper, it is assumed, for all
. Throughout the paper, it is assumed, for all  and
and  appeared in (1.1) and (1.2), that
appeared in (1.1) and (1.2), that  for all
for all  ;
;  ;
;  is a quotient of odd integers.
is a quotient of odd integers.
It is well known from relevant literature that there have been deep and thorough studies on the nonoscillatory behaviour of solutions of second- and third-order nonlinear differential equations in recent years. See, for instance, [1–37] as some related papers or books on the subject. In the most of these studies the following differential equation and some special cases of

have been investigated. However, much less work has been done for nonoscillation of all solutions of nonlinear functional differential equations. In this connection, Parhi [10] established some sufficient conditions for oscillation of all solutions of the second-order forced differential equation of the form

and nonoscillation of all bounded solutions of the equations

where the real-valued functions  ,
,  ,
,  ,
,  ,
,  , and
, and  are continuous on
are continuous on  with
with  and
and  ;
;  ,
,  for
for  ;
;  ,
,  , and both
, and both  and
and  are quotients of odd integers.
are quotients of odd integers.
Later, Nayak and Choudhury [5] considered the differential equation

and they gave certain sufficient conditions on the functions involved for all bounded solutions of the above equation to be nonoscillatory.
Recently, in 2007, Tunç [23] investigated nonoscillation of solutions of the third-order differential equations:

The motivation for the present work has come from the paper of Parhi [10], Tunç [23] and the papers mentioned above. We restrict our considerations to the real solutions of (1.1) and (1.2) which exist on the half-line  , where
, where  (
( ) depends on the particular solution, and are nontrivial in any neighborhood of infinity. It is well known that a solution
) depends on the particular solution, and are nontrivial in any neighborhood of infinity. It is well known that a solution  of (1.1) or (1.2) is said to be nonoscillatory on
of (1.1) or (1.2) is said to be nonoscillatory on  if there exists a
if there exists a  such that
such that  for
for  ; it is said to be oscillatory if for any
; it is said to be oscillatory if for any  there exist
there exist  and
and  satisfying
satisfying  such that
such that  and
and  ;
;  is said to be a
is said to be a  -type solution if it has arbitrarily large zeros but is ultimately nonnegative or nonpositive.
-type solution if it has arbitrarily large zeros but is ultimately nonnegative or nonpositive.
2. Nonoscillation Behaviors of Solutions of (1.1)
In this section, we obtain sufficient conditions for the nonoscillation of solutions of (1.1).
Theorem 2.1.
Let  . If
. If  , then all bounded solutions of (1.1) are nonoscillatory.
, then all bounded solutions of (1.1) are nonoscillatory.
Proof.
Let  be a bounded solution of (1.1) on
be a bounded solution of (1.1) on  ,
,  , such that
, such that  for
for  . Since
. Since  , there exists a
, there exists a  such that
such that  for
for  . In view of the assumption
. In view of the assumption  , it follows that there exists a
, it follows that there exists a  such that
such that  for
for  . If possible, let
. If possible, let  be of nonnegative
be of nonnegative  -type solution with consecutive double zeros at
-type solution with consecutive double zeros at  and
and  (
( ) such that
) such that  for
for  . So, there exists
. So, there exists  such that
such that  and
and  for
for  . Multiplying (1.1) through by
. Multiplying (1.1) through by  , we get
, we get

Integrating (2.1) from  to
to  , we obtain
, we obtain

which is a contradiction.
Let  be of nonpositive
be of nonpositive  -type solution with consecutive double zeros at
-type solution with consecutive double zeros at  and
and  (
( ). Then, there exists a
). Then, there exists a  such that
such that  and
and  for
for  .
.
Integrating (2.1) from  to
to  yields
yields

which is a contradiction.
If possible, let  be oscillatory with consecutive zeros at
be oscillatory with consecutive zeros at  ,
,  and
and  (
( ) such that
) such that  ,
,  ,
,  ,
,  for
for  and
and  for
for  . So there exists points
. So there exists points  and
and  such that
such that  ,
,  ,
,  for
for  and
and  for
for  . Now integrating (2.1) from
. Now integrating (2.1) from  to
to  , we get
, we get

which is a contradiction. This completes the proof of Theorem 2.1.
Remark 2.2.
For the special case  ,
,  , Theorem 2.1 has been proved by Tunç [23]. Our results include the results established in Tunç [23].
, Theorem 2.1 has been proved by Tunç [23]. Our results include the results established in Tunç [23].
Theorem 2.3.
Let  and
and  , then all solutions
, then all solutions  of (1.1) which satisfy the inequality
of (1.1) which satisfy the inequality

on any interval where  are nonoscillatory.
are nonoscillatory.
Proof.
Let  be a solution of (1.1) on
be a solution of (1.1) on  ,
,  . Due to
. Due to  , there exists a
, there exists a  such that
such that  for
for  . If possible, let
. If possible, let  be of nonnegative
be of nonnegative  -type solution with consecutive double zeros at
-type solution with consecutive double zeros at  and
and  (
( ) such that
) such that  for
for  . So, there exists a
. So, there exists a  such that
such that  and
and  for
for  . Integrating (2.1) from
. Integrating (2.1) from  to
to  , we get
, we get

which is a contradiction.
Next, let  be of nonpositive
be of nonpositive  -type solution with consecutive double zeros at
-type solution with consecutive double zeros at  and
and  (
( ). Then, there exists
). Then, there exists  such that
such that  and
and  for
for  .
.
Integrating (2.1) from  to
to  , we have
, we have

which is a contradiction.
Now, if possible let  be oscillatory with consecutive zeros at
be oscillatory with consecutive zeros at  ,
,  and
and  (
( ) such that
) such that  ,
,  ,
,  ,
,  for
for  and
and  for
for  . Hence, there exist
. Hence, there exist  and
and  such that
such that  and
and  for
for  and
and  . Integrating (2.1) from
. Integrating (2.1) from  to
to  , we obtain
, we obtain

which is a contradiction. This completes the proof of Theorem 2.3.
Remark 2.4.
For the special case  ,
,  , Theorem 2.3 has been proved by Tunç [25]. Our results include the results established in Tunç [25].
, Theorem 2.3 has been proved by Tunç [25]. Our results include the results established in Tunç [25].
3. Nonoscillation Behaviors of Solutions (1.2)
In this section, we give sufficient conditions so that all solutions of (1.2) are nonoscillatory.
Theorem 3.1.
Suppose that  and
and  . If
. If  is a solution (1.2) such that it satisfies the inequality
is a solution (1.2) such that it satisfies the inequality

on any interval where  , then
, then  is nonoscillatory.
is nonoscillatory.
Proof.
Let  be a solution of (1.2) on
be a solution of (1.2) on  ,
,  . Due to
. Due to  , there exists a
, there exists a  such that
such that  for
for  . If possible, let
. If possible, let  be of nonnegative
be of nonnegative  -type solution with consecutive double zeros at
-type solution with consecutive double zeros at  and
and  (
( ) such that
) such that  for
for  . So, there exists a
. So, there exists a  such that
such that  and
and  for
for  . Multiplying (1.2) through by
. Multiplying (1.2) through by  , we get
, we get

Integrating (3.2) from  to
to  , we get
, we get

which is a contradiction.
Next, let  be of nonpositive
be of nonpositive  -type solution with consecutive double zeros at
-type solution with consecutive double zeros at  and
and  (
( ). Then, there exists
). Then, there exists  such that
such that  and
and  for
for  .
.
Integrating (3.2) from  to
to  , we have
, we have

which is a contradiction.
Now, if possible let  be oscillatory with consecutive zeros at
be oscillatory with consecutive zeros at  ,
,  and
and  (
( ) such that
) such that  ,
,  ,
,  ,
,  for
for  and
and  for
for  . Hence, there exist
. Hence, there exist  and
and  such that
such that  and
and  for
for  and
and  . Integrating (3.2) from
. Integrating (3.2) from  to
to  , we obtain
, we obtain

which is a contradiction. This completes the proof of Theorem 3.1.
Theorem 3.2.
Suppose that  and
and  on any subinterval of
on any subinterval of  ,
,  . If
. If  is a solution of (1.2) such that it satisfies the inequality
is a solution of (1.2) such that it satisfies the inequality

on any subinteval of  ,
,  , where
, where  , then
, then  is nonoscillatory.
is nonoscillatory.
Proof.
Let  be a solution of (1.2) on
be a solution of (1.2) on  ,
,  . Since
. Since  , there exists a
, there exists a  such that
such that  for
for  . If possible, let
. If possible, let  be of nonnegative
be of nonnegative  -type solution with consecutive double zeros at
-type solution with consecutive double zeros at  and
and  (
( ) such that
) such that  for
for  . So, there exists a
. So, there exists a  such that
such that  and
and  for
for  . Integrating (3.2) from
. Integrating (3.2) from  to
to  , we get
, we get

which is a contradiction.
Next, let  be of nonpositive
be of nonpositive  -type solution with consecutive double zeros at
-type solution with consecutive double zeros at  and
and  (
( ). Then, there exists
). Then, there exists  such that
such that  and
and  for
for  .
.
Integrating (3.2) from  to
to  , we have
, we have

which is a contradiction.
Now, if possible let  be oscillatory with consecutive zeros at
be oscillatory with consecutive zeros at  ,
,  and
and  (
( ) such that
) such that  ,
,  ,
,  ,
,  for
for  and
and  for
for  . Hence, there exist
. Hence, there exist  and
and  such that
such that  and
and  for
for  and
and  . Integrating (3.2) from
. Integrating (3.2) from  to
to  , we obtain
, we obtain

which is a contradiction. This completes the proof of Theorem 3.2.
Remark 3.3.
It is clear that Theorem 3.2 is not applicable to homogeneous equations:

where  and
and  .
.
Remark 3.4.
For the special case  ,
,  , Theorem 3.2 has been proved by N. parhi and S. parhi [19, Theorem 2.7].
, Theorem 3.2 has been proved by N. parhi and S. parhi [19, Theorem 2.7].
Theorem 3.5.
Let  ,
,  and
and  for all
for all  . If
. If  and
and  are once continuously differentiable functions such that
are once continuously differentiable functions such that  ,
,  and
and  , then all solutions
, then all solutions  of (1.2) for which
of (1.2) for which  ultimately are nonoscillatory.
ultimately are nonoscillatory.
Proof.
Let  be a solution of (1.2) on
be a solution of (1.2) on  ,
,  , such that
, such that  for
for  . Since
. Since  , there exists a
, there exists a  such that
such that  for
for  . If possible, let
. If possible, let  be of nonnegative
be of nonnegative  -type solution with consecutive double zeros at
-type solution with consecutive double zeros at  and
and  (
( ) such that
) such that  for
for  . So, there exists a
. So, there exists a  such that
such that  and
and  for
for  . Integrating (3.2) from
. Integrating (3.2) from  to
to  , we get
, we get

But

Therefore

since  for
for  . So (3.11) yields
. So (3.11) yields

which is a contradiction.
Next, let  be of nonpositive
be of nonpositive  -type solution with consecutive double zeros at
-type solution with consecutive double zeros at  and
and  (
( ). Then, there exists
). Then, there exists  such that
such that  and
and  for
for  .
.
Integrating (3.2) from  to
to  , we have
, we have

which is a contradiction.
Now, if possible let  be oscillatory with consecutive zeros at
be oscillatory with consecutive zeros at  ,
,  and
and  (
( ) such that
) such that  ,
,  ,
,  ,
,  for
for  and
and  for
for  . So there exist
. So there exist  and
and  such that
such that  ,
,  and
and  for
for  . We consider two cases, namely,
. We consider two cases, namely,  and
and  . Suppose that
. Suppose that  . Integrating (3.2) from
. Integrating (3.2) from  to
to  , we get
, we get

which is a contradiction. Let  . Integrating (3.2) from
. Integrating (3.2) from  to
to  , we get
, we get

We proceed as in nonnegative  -type to conclude that
-type to conclude that  . This is a contradiction. So
. This is a contradiction. So  is nonoscillatory. This completes the proof of Theorem 3.5.
is nonoscillatory. This completes the proof of Theorem 3.5.
Remark 3.6.
If  in Theorem 3.5, then
in Theorem 3.5, then  and hence the theorem is not applicable to homogeneous equation:
and hence the theorem is not applicable to homogeneous equation:

References
Grace SR, Lalli BS: On oscillation and nonoscillation of general functional-differential equations. Journal of Mathematical Analysis and Applications 1985,109(2):522–533. 10.1016/0022-247X(85)90166-0
Graef JR, Greguš M: Oscillatory properties of solutions of certain nonlinear third order differential equations. Nonlinear Studies 2000,7(1):43–50.
Hartman P: Ordinary Differential Equations, Classics in Applied Mathematics. SIAM, Philadelphia, Pa, USA; 2002.
Kartsatos AG, Manougian MN: Perturbations causing oscillations of functional-differential equations. Proceedings of the American Mathematical Society 1974, 43: 111–117. 10.1090/S0002-9939-1974-0328270-3
Nayak PC, Choudhury R: Oscillation and nonoscillation theorems for third order functional-differential equation. The Journal of the Indian Mathematical Society. (New Series) 1996,62(1–4):89–96.
Padhi S: On oscillatory solutions of third order differential equations. Memoirs on Differential Equations and Mathematical Physics 2004, 31: 109–111.
Padhi S: On oscillatory linear third order forced differential equations. Differential Equations and Dynamical Systems 2005,13(3–4):343–358.
Parhi N: Nonoscillatory behaviour of solutions of nonhomogeneous third order differential equations. Applicable Analysis 1981,12(4):273–285. 10.1080/00036818108839368
Parhi N: Nonoscillation of solutions of a class of third order differential equations. Acta Mathematica Hungarica 1989,54(1–2):79–88. 10.1007/BF01950712
Parhi N: Sufficient conditions for oscillation and nonoscillation of solutions of a class of second order functional-differential equations. Analysis 1993,13(1–2):19–28.
Parhi N: On non-homogeneous canonical third-order linear differential equations. Australian Mathematical Society Journal 1994,57(2):138–148. 10.1017/S1446788700037472
Parhi N, Das P: Oscillation criteria for a class of nonlinear differential equations of third order. Annales Polonici Mathematici 1992,57(3):219–229.
Parhi N, Das P: On asymptotic property of solutions of linear homogeneous third order differential equations. Unione Matematica Italiana. Bollettino B. Series VII 1993,7(4):775–786.
Parhi N, Das P: Oscillatory and asymptotic behaviour of a class of nonlinear functional-differential equations of third order. Bulletin of the Calcutta Mathematical Society 1994,86(3):253–266.
Parhi N, Das P: On nonoscillation of third order differential equations. Bulletin of the Institute of Mathematics Academia Sinica 1994,22(3):267–274.
Parhi N, Padhi S: On oscillatory linear differential equations of third order. Archivum Mathematicum, Universitatis Masarykianae Brunensis 2001,37(1):33–38.
Parhi N, Padhi S: On oscillatory linear third order differential equations. The Journal of the Indian Mathematical Society. (New Series) 2002,69(1–4):113–128.
Parhi N, Parhi S: Oscillation and nonoscillation theorems for nonhomogeneous third order differential equations. Bulletin of the Institute of Mathematics Academia Sinica 1983,11(2):125–139.
Parhi N, Parhi S: Nonoscillation and asymptotic behaviour for forced nonlinear third order differential equations. Bulletin of the Institute of Mathematics. Academia Sinica 1985,13(4):367–384.
Parhi N, Parhi S: On the behaviour of solutions of the differential equations
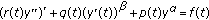 . Polska Akademia Nauk. Annales Polonici Mathematici 1986,47(2):137–148.
. Polska Akademia Nauk. Annales Polonici Mathematici 1986,47(2):137–148.Parhi N, Parhi S: Qualitative behaviour of solutions of forced nonlinear third order differential equations. Rivista di Matematica della Università di Parma. Serie IV 1987, 13: 201–210.
Swanson CA: Comparison and Oscillation Theory of Linear Differential Equations, Mathematics in Science and Engineering. Volume 48. Academic Press, New York, NY, USA; 1968:viii+227.
Tunç C: On the non-oscillation of solutions of some nonlinear differential equations of third order. Nonlinear Dynamics and Systems Theory 2007,7(4):419–430.
Tunç C: On the nonoscillation of solutions of nonhomogeneous third order differential equations. Soochow Journal of Mathematics 1997,23(1):1–7.
Tunç C: Non-oscillation criteria for a class of nonlinear differential equations of third order. Bulletin of the Greek Mathematical Society 1997, 39: 131–137.
Tunç C, Tunç E: On the asymptotic behavior of solutions of certain second-order differential equations. Journal of the Franklin Institute, Engineering and Applied Mathematics 2007,344(5):391–398. 10.1016/j.jfranklin.2006.02.011
Tunç C: Uniform ultimate boundedness of the solutions of third-order nonlinear differential equations. Kuwait Journal of Science & Engineering 2005,32(1):39–48.
Tunç E: On the convergence of solutions of certain third-order differential equations. Discrete Dynamics in Nature and Society 2009, 2009:-12.
Tunç E: Periodic solutions of a certain vector differential equation of sixth order. The Arabian Journal for Science and Engineering A 2008,33(1):107–112.
Tunç C: A new boundedness theorem for a class of second order differential equations. The Arabian Journal for Science and Engineering A 2008,33(1):1–10.
Zhong X-Z, Xing H-L, Shi Y, Liang J-C, Wang D-H: Existence of nonoscillatory solution of third order linear neutral delay difference equation with positive and negative coefficients. Nonlinear Dynamics and Systems Theory 2005,5(2):201–214.
Zhong X, Liang J, Shi Y, Wang D, Ge L: Existence of nonoscillatory solution of high-order nonlinear difference equation. Nonlinear Dynamics and Systems Theory 2006,6(2):205–210.
Zayed EME, El-Moneam MA: Some oscillation criteria for second order nonlinear functional ordinary differential equations. Acta Mathematica Scientia B 2007,27(3):602–610. 10.1016/S0252-9602(07)60059-9
Zayed EME, Grace SR, El-Metwally H, El-Moneam MA: The oscillatory behavior of second order nonlinear functional differential equations. The Arabian Journal for Science and Engineering A 2006,31(1):23–30.
Grace SR, Lalli BS, Yeh CC: Oscillation theorems for nonlinear second order differential equations with a nonlinear damping term. SIAM Journal on Mathematical Analysis 1984,15(6):1082–1093. 10.1137/0515084
Grace SR: Oscillation criteria for forced functional-differential equations with deviating arguments. Journal of Mathematical Analysis and Applications 1990,145(1):63–88. 10.1016/0022-247X(90)90432-F
Grace SR, Hamedani GG: On the oscillation of functional-differential equations. Mathematische Nachrichten 1999, 203: 111–123.
Acknowledgment
The author would like to express sincere thanks to the anonymous referees for their invaluable corrections, comments, and suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Tunç, E. New Results on the Nonoscillation of Solutions of Some Nonlinear Differential Equations of Third Order. J Inequal Appl 2009, 896934 (2009). https://doi.org/10.1155/2009/896934
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/896934
 . Polska Akademia Nauk. Annales Polonici Mathematici 1986,47(2):137–148.
. Polska Akademia Nauk. Annales Polonici Mathematici 1986,47(2):137–148.