- Research Article
- Open access
- Published:
Sufficient and Necessary Conditions for Oscillation of  th-Order Differential Equation with Retarded Argument
th-Order Differential Equation with Retarded Argument
Journal of Inequalities and Applications volume 2009, Article number: 892936 (2009)
Abstract
Necessary and sufficient conditions are found for oscillation of the solutions of a class of strongly superlinear and strongly sublinear differential equations of even order with retarded argument.
1. Introduction
We consider the following  th-order differential equation with retarded argument:
th-order differential equation with retarded argument:

Firstly, we introduce several conditions as follows:
() ,
,  for
for  and
and  .
.
() ,
,  for
for  and
and  .
.
As customary, a solution of (1.1) is said to be oscillatory if it has arbitrarily large zeros. Otherwise the solution is called nonoscillatory.
Definition 1.1.
The function  is said to be strongly superlinear if there exists
is said to be strongly superlinear if there exists  , such that
, such that  is a nondecreasing function with respect to
is a nondecreasing function with respect to  for each fixed
for each fixed 
It is easy to see that the function  is nondecreasing with respect to
is nondecreasing with respect to  for
for  if
if  is strongly superlinear. The function
is strongly superlinear. The function  is nondecreasing with respect to
is nondecreasing with respect to  for
for  if
if  is nondecreasing with respect to
is nondecreasing with respect to  .
.
Definition 1.2.
The function  is said to be strongly sublinear if there exists
is said to be strongly sublinear if there exists  , such that
, such that  is a nonincreasing function with respect to
is a nonincreasing function with respect to  for each fixed
for each fixed 
We should indicate that there are many ways in which one can define the concept of strongly superlinearity, superlinearity, strongly sublinearity and sublinearity, to characterize functions satisfying different conditions. For example, in [1] the strongly superlinearity is used to specify functions with specific behavior at 0 and  ; in [2] the superlinearity and sublinearity are defined for multivariable functions. In this paper, we adopt the definitions as in monograph [3].
; in [2] the superlinearity and sublinearity are defined for multivariable functions. In this paper, we adopt the definitions as in monograph [3].
In particular, if  where
where  ,
,  and
and  is the quotient of odd positive integers, then (1.1) becomes
is the quotient of odd positive integers, then (1.1) becomes

It is easy to see that  is strongly superlinear for
is strongly superlinear for  and
and  is strongly sublinear for
is strongly sublinear for  . If
. If  ; then (1.2) reduces to
; then (1.2) reduces to

Equation (1.3) is the well-known Emden-Fowler equation [4].
Recently, many remarkable results have been established for the oscillation of solutions of the second- and higher-order functional differential equations. For example, Theorem A is presented in [2].
Theorem A
If  , then every bounded solution of (1.2) oscillates if and only if
, then every bounded solution of (1.2) oscillates if and only if

For (1.3), the well-known Theorems B–D are presented in [5–7].
If  , then (1.3) has a bounded nonoscillatory solution if and only if
, then (1.3) has a bounded nonoscillatory solution if and only if

Theorem C [see [5]]
If  , then all solutions of (1.3) are oscillatory if and only if
, then all solutions of (1.3) are oscillatory if and only if

Theorem D [see [7]]
If  , then (1.3) is oscillatory if and only if
, then (1.3) is oscillatory if and only if

In [8], Waltman studied the oscillation of the solutions for the equation

Equation (1.8) is the prototype of (1.1) and (1.2). Theorems E and F were proved in [8].
Theorem E
If  satisfies (i)
satisfies (i) and
and  for
for  and (ii)
and (ii) is continuous and non-negative, then (1.8) has a bounded and eventually monotonic solution if and only if
is continuous and non-negative, then (1.8) has a bounded and eventually monotonic solution if and only if

Theorem F
Suppose that the conditions (i) and (ii) in Theorem E are satisfied. If

for some  , then all solutions of (1.8) are oscillatory if and only if
, then all solutions of (1.8) are oscillatory if and only if

Some other related results can be found in [2, 4, 9–12] and the references cited therein. Due to some problems of theoretical and technical character in handling with higher-order nonlinear differential equations, there are only a few results which concern necessary and sufficient conditions for the oscillatory behavior for (1.1). So there are a lot of things worth further consideration for (1.1). The main purpose of this paper is to establish necessary and sufficient conditions for (1.1). The obtained results extend the above theorems.
2. Main Results
In order to establish our main results we need introduce and establish two lemmas.
If  is a positive and
is a positive and  -times differentiable function on
-times differentiable function on  , and
, and  is nonpositive and not identically zero on any subinterval
is nonpositive and not identically zero on any subinterval  , then there exist
, then there exist  and an integer
and an integer  such that
such that  is odd and
is odd and
(i) for
for  ,
,  ,
, 
(ii) for
for 
(iii) for
for  ,
,  ,
, 
Lemma 2.2.
If  is a strongly sublinear function, then
is a strongly sublinear function, then

for  and
and  .
.
Proof.
From  and
and  together with Definition 1.2 we clearly see that
together with Definition 1.2 we clearly see that

where  . From
. From  we know that
we know that  , and therefore
, and therefore

Our main result is Theorem 2.3.
Theorem 2.3.
The following statements are true.
-
(a)
Suppose that
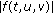 is a nondecreasing function with respect to
is a nondecreasing function with respect to 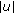 and
and 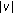 for
for 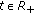 . If
. If

for some constants  , then (1.1) has a bounded nonoscillatory solution.
, then (1.1) has a bounded nonoscillatory solution.
-
(b)
If
 is a strongly superlinear function, then every solution of (1.1) oscillates if and only if
is a strongly superlinear function, then every solution of (1.1) oscillates if and only if

for any  .
.
-
(c)
If
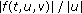 is a nondecreasing function with respect to
is a nondecreasing function with respect to 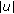 and
and 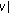 , then every bounded solution of (1.1) oscillates if and only if
, then every bounded solution of (1.1) oscillates if and only if

for each  .
.
-
(d)
If
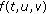 is a strongly sublinear function, then every solution of (1.1) oscillates if and only if
is a strongly sublinear function, then every solution of (1.1) oscillates if and only if

for any  .
.
Proof.
-
(a)
Assume that (2.4) holds. Choose
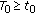 sufficiently large such that
sufficiently large such that

for  and some
and some  .
.
Observing that if  satisfies the equation
satisfies the equation

then  is a solution of (1.1). Therefore it suffices to show that (2.9) has a bounded nonoscillatory solution.
is a solution of (1.1). Therefore it suffices to show that (2.9) has a bounded nonoscillatory solution.
Consider the functional set

Define the operator  as follows:
as follows:

Then we have

Clearly, we have  , and therefore
, and therefore  .
.
Now, we define the functions  as follows:
as follows:

where

Since the function  is nondecreasing with respect to
is nondecreasing with respect to  and
and  , a straightforward verification shows the validity of the inequalities
, a straightforward verification shows the validity of the inequalities

Therefore  for
for  It follows from the Lebesgue convergence theorem that
It follows from the Lebesgue convergence theorem that  and
and  .
.
It is easy to see that  is the desired bounded and nonoscillatory solution of (2.9)
is the desired bounded and nonoscillatory solution of (2.9)
-
(b)
Sufficiency. Assume that
 for each
for each 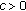 . We will prove that every solution of (1.1) oscillates. Otherwise, assume that (1.1) has a nonoscillatory solution
. We will prove that every solution of (1.1) oscillates. Otherwise, assume that (1.1) has a nonoscillatory solution 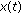 . Without loss of generality, assume that
. Without loss of generality, assume that 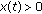 for
for  . Then according to Lemma 2.1, there exists an odd integer
. Then according to Lemma 2.1, there exists an odd integer  and
and 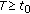 such that
such that

There are two possible cases.
Case 1 ( ).
).
In this case we see that

Since  is an increasing function, hence for
is an increasing function, hence for  and some constants
and some constants  , one has
, one has

Making use of the Taylor expansion we get

From (1.1) and (2.17) together with (2.19) we get

The strong superlinearity of  leads to
leads to

which implies

From (2.22) we have

By using the elementary inequality  for
for  , we have
, we have

Therefore, we get


or

which contradicts with (2.5).
Case 2 ( ).
).
Making use of (2.21) we have

For  , it follows from (iii) of Lemma 2.1 that
, it follows from (iii) of Lemma 2.1 that

For sufficiently large  , one has
, one has

Let  , then
, then

and therefore

Using the same method as in the proof of Case 1, we get

that is

which contradicts with (2.5).
Conversely, if every solution of (1.1) oscillates, then (2.5) holds. Otherwise (2.4) holds. Theorem 2.3(a) implies that (1.1) has a nonoscillatory solution.
-
(c)
Sufficiency. Without loss of generality, we assume that
 is a bounded positive solution. We divided the proof into two cases.
is a bounded positive solution. We divided the proof into two cases.
Case 1 ( ).
).
The same argument as in the proof of Theorem 2.3(b) implies that inequality (2.26) holds for  , that is,
, that is,

which contradicts with (2.6).
Case 2 ( ).
).
From the proof of Theorem 2.3(b) we also clearly see that

which contradicts with (2.6).
Conversely, if every bounded solution of (1.1) oscillates, and then (2.6) holds. Otherwise (2.4) holds, then Theorem 2.3(a) implies that (1.1) has a nonoscillatory bounded solution.
-
(d)
Sufficiency. Without loss of generality, we assume that
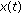 is a finally positive solution, that is,
is a finally positive solution, that is, 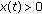 for
for 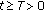 . We consider the following two cases.
. We consider the following two cases.
Case 1 ( ).
).
In this case we see that

then we know that

and there exist constants  and
and  such that
such that  and
and  for
for  The strong sublinearity of
The strong sublinearity of  implies that
implies that

The same argument as in the proof of Case 1 of Theorem 2.3(b) yields

Integrating from  to
to  leads to
leads to

That is

Let

then  ,
,  and
and

and for  , one has
, one has

Therefore

or

By condition (H2), we can choose  such that
such that  and
and  for
for  . Then making use of Lemma 2.2, we have
. Then making use of Lemma 2.2, we have

From (2.47) and (2.48) together with  we get
we get

which contradicts with (2.7).
Case 2 ( ).
).
That is,

From  and
and  for
for  we know that
we know that

and there exist constants  and
and  such that
such that  and
and  for
for  The strong sublinearity of
The strong sublinearity of  leads to
leads to

It follows from (iii) of Lemma 2.1, that

and thus

Let  , then
, then  ,
,  ,
,  and
and

where  is also even. According to the same process as the one used in the proof of Case 1 of Theorem 2.3(d) we conclude that
is also even. According to the same process as the one used in the proof of Case 1 of Theorem 2.3(d) we conclude that

By condition (H2), we can choose  such that
such that  and
and  for
for  . Now making use of Lemma 2.2, we have
. Now making use of Lemma 2.2, we have

From (2.56) and (2.57) together with  we clearly see that
we clearly see that

which contradicts with (2.7).
Necessity.
If every solution of (1.1) oscillates, then (2.7) holds. Otherwise, assuming that

for some constants  , we should prove that (1.1) has a nonoscillatory solution. From (2.59) we know that there exist
, we should prove that (1.1) has a nonoscillatory solution. From (2.59) we know that there exist  and some
and some  such that
such that

Let  be the Banach space of all real-valued continuous functions
be the Banach space of all real-valued continuous functions  endowed with the norm
endowed with the norm

and let  be the subset of
be the subset of  defined by
defined by

Define the mapping  on
on  by
by

where the integration is  times.
times.
By Lemma 2.2, for  one has
one has

for sufficient large  , that is,
, that is,

From (2.60) and (2.65) we get

Equation (2.66) and the definition of the operator  imply that
imply that  . On the other hand, we clearly see that
. On the other hand, we clearly see that  for
for  . Therefore,
. Therefore,  .
.
It is routine to prove that  is continuous and
is continuous and  is relatively compact in the topology of the Frechet space
is relatively compact in the topology of the Frechet space  . Therefore, there exists
. Therefore, there exists  such that
such that  follows from the well-known Schauder's fixed point Theorem. It is easy to see that
follows from the well-known Schauder's fixed point Theorem. It is easy to see that  is the solution of (1.1).
is the solution of (1.1).
The proof of Theorem 2.3 is completed.
Remark 2.4.
If  , then
, then  and
and  . For (1.2) we can derive Corollary 2.5 from Theorem 2.3.
. For (1.2) we can derive Corollary 2.5 from Theorem 2.3.
Corollary 2.5.
If  is even, then the following statements are true.
is even, then the following statements are true.
-
(a)
If

then (1.2) has a bounded nonoscillatory solution.
-
(b)
If
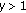 , then every solution of (1.2) oscillates if and only if
, then every solution of (1.2) oscillates if and only if

(c) If  , then every bounded solution of (1.2) oscillates if and only if
, then every bounded solution of (1.2) oscillates if and only if

(d) If  , then every solution of (1.2) oscillates if and only if
, then every solution of (1.2) oscillates if and only if

It is easy to see that Theorem A can be obtained directly from our Corollary 2.5(c).
For  , we have Corollary 2.6 for (1.3).
, we have Corollary 2.6 for (1.3).
Corollary 2.6.
If  , then the following statements are true.
, then the following statements are true.
-
(a)
If

then (1.3) has a bounded nonoscillatory solution.
-
(b)
If
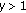 , then every solution of (1.3) oscillates if and only if
, then every solution of (1.3) oscillates if and only if

(c) If  , then every bounded solution of (1.3) oscillates if and only if
, then every bounded solution of (1.3) oscillates if and only if

(d) If  , then every solution of (1.3) oscillates if and only if
, then every solution of (1.3) oscillates if and only if

We clearly see that our results in Corollary 2.6(a), (b), and (d) are exactly corresponding to the results in Theorems B, C, and D, respectively.
Remark 2.7.
If  , then (1.1) becomes
, then (1.1) becomes

From the proof of Theorem 2.3(b) we indicate that the strongly superlinearity of  can be replaced by the condition
can be replaced by the condition

In fact, if  is a nonoscillatory solution of (2.75), then from Theorem 2.3(a) we may assume that
is a nonoscillatory solution of (2.75), then from Theorem 2.3(a) we may assume that  is unbounded, and (2.76) implies that
is unbounded, and (2.76) implies that  , and there exists
, and there exists  such that
such that  and
and  for
for  . Then we get
. Then we get

We notice that if (2.21) is replaced by (2.77), then Corollary 2.8 follows from the proof of Theorem 2.3(b).
Corollary 2.8.
If  , then all solutions of (2.75) oscillate if and only if
, then all solutions of (2.75) oscillate if and only if

If  , then one clearly sees that Theorem F is the special case of Corollary 2.8.
, then one clearly sees that Theorem F is the special case of Corollary 2.8.
Example 2.9.
The equation

satisfies the assumptions of Theorem 2.3(a) but does not satisfy the assumptions of Theorem 2.3(b) and (c); hence there exists a bounded nonoscillatory solution. In fact  is one such solution.
is one such solution.
Example 2.10.
The equation

satisfies the assumptions of Theorem 2.3(d). Hence every solution of (1.1) is oscillatory. In fact  is one such solution.
is one such solution.
References
Philos ChG: Oscillation criteria for second order superlinear differential equations. Canadian Journal of Mathematics 1989,41(2):321–340. 10.4153/CJM-1989-016-3
Erbe LH, Kong Q, Zhang BG: Oscillation Theory for Functional-Differential Equations, Monographs and Textbooks in Pure and Applied Mathematics. Volume 190. Marcel Dekker, New York, NY, USA; 1995:viii+482.
Bainov D, Simeonov P: Oscillation Theory of Impulsive Differential Equations. International Publications, Orlando, Fla, USA; 1998:ii+284.
Wong JSW: On the generalized Emden-Fowler equation. SIAM Review 1975, 17: 339–360. 10.1137/1017036
Atkinson FV: On second-order non-linear oscillations. Pacific Journal of Mathematics 1955, 5: 643–647.
Belohorec Š: Oscillatory solutions of certain nonlinear differential equations of the second order. Matematicky Časopis Slovenskej Akadémie Vied 1961, 11: 250–254.
Belohorec Š: Monotone and oscillatory solutions of a class of nonlinear differential equations. Matematicky Časopis Slovenskej Akadémie Vied 1969, 19: 169–187.
Waltman P: Oscillation of solutions of a nonlinear equation. SIAM Review 1963, 5: 128–130. 10.1137/1005032
Agarwal RP, Bohner M, Li W-T: Nonoscillation and Oscillation: Theory for Functional Differential Equations, Monographs and Textbooks in Pure and Applied Mathematics. Volume 267. Marcel Dekker, New York, NY, USA; 2004:viii+376.
Agarwal RP, Grace SR, O'Regan D: Oscillation Theory for Difference and Functional Differential Equations. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2000:viii+337.
Agarwal RP, Grace SR, O'Regan D: Oscillation Theory for Second Order Dynamic Equations, Series in Mathematical Analysis and Applications. Volume 5. Taylor & Francis, London, UK; 2003:viii+404.
Kamenev IV: An integral test for conjugacy for second order linear differential equations. Matematicheskie Zametki 1978,23(2):249–251.
Kiguradze IT: On the oscillatory character of solutions of the equation
 . Matematicheskiĭ Sbornik 1964,65(107):172–187.
. Matematicheskiĭ Sbornik 1964,65(107):172–187.Markova NT, Simeonov PS: Oscillation theorems for
 -th order nonlinear differential equations with forcing terms and deviating arguments depending on the unknown function. Communications in Applied Analysis 2005,9(3–4):417–427.
-th order nonlinear differential equations with forcing terms and deviating arguments depending on the unknown function. Communications in Applied Analysis 2005,9(3–4):417–427.Markova NT, Simeonov PS: Asymptotic and oscillatory behavior of
 -th order forced differential equations with deviating argument depending on the unknown function. Panamerican Mathematical Journal 2006,16(1):1–15.
-th order forced differential equations with deviating argument depending on the unknown function. Panamerican Mathematical Journal 2006,16(1):1–15.
Acknowledgments
The authors wish to thank the anonymous referees for the very careful reading of the manuscript and fruitful comments and suggestions. This work was supported by the National Natural Science Foundation of China (Grant no. 60850005) and the Natural Science Foundation of Zhejiang Province (Grant nos. D7080080 and Y607128).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cheng, Jf., Chu, Ym. Sufficient and Necessary Conditions for Oscillation of  th-Order Differential Equation with Retarded Argument.
J Inequal Appl 2009, 892936 (2009). https://doi.org/10.1155/2009/892936
th-Order Differential Equation with Retarded Argument.
J Inequal Appl 2009, 892936 (2009). https://doi.org/10.1155/2009/892936
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/892936
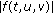 is a nondecreasing function with respect to
is a nondecreasing function with respect to 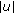 and
and 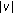 for
for 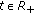 . If
. If is a strongly superlinear function, then every solution of (1.1) oscillates if and only if
is a strongly superlinear function, then every solution of (1.1) oscillates if and only if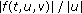 is a nondecreasing function with respect to
is a nondecreasing function with respect to 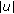 and
and 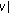 , then every bounded solution of (1.1) oscillates if and only if
, then every bounded solution of (1.1) oscillates if and only if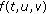 is a strongly sublinear function, then every solution of (1.1) oscillates if and only if
is a strongly sublinear function, then every solution of (1.1) oscillates if and only if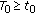 sufficiently large such that
sufficiently large such that for each
for each 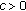 . We will prove that every solution of (1.1) oscillates. Otherwise, assume that (1.1) has a nonoscillatory solution
. We will prove that every solution of (1.1) oscillates. Otherwise, assume that (1.1) has a nonoscillatory solution 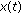 . Without loss of generality, assume that
. Without loss of generality, assume that 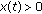 for
for  . Then according to Lemma 2.1, there exists an odd integer
. Then according to Lemma 2.1, there exists an odd integer  and
and 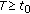 such that
such that is a bounded positive solution. We divided the proof into two cases.
is a bounded positive solution. We divided the proof into two cases.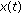 is a finally positive solution, that is,
is a finally positive solution, that is, 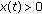 for
for 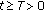 . We consider the following two cases.
. We consider the following two cases.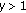 , then every solution of (1.2) oscillates if and only if
, then every solution of (1.2) oscillates if and only if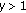 , then every solution of (1.3) oscillates if and only if
, then every solution of (1.3) oscillates if and only if . Matematicheskiĭ Sbornik 1964,65(107):172–187.
. Matematicheskiĭ Sbornik 1964,65(107):172–187. -th order nonlinear differential equations with forcing terms and deviating arguments depending on the unknown function. Communications in Applied Analysis 2005,9(3–4):417–427.
-th order nonlinear differential equations with forcing terms and deviating arguments depending on the unknown function. Communications in Applied Analysis 2005,9(3–4):417–427. -th order forced differential equations with deviating argument depending on the unknown function. Panamerican Mathematical Journal 2006,16(1):1–15.
-th order forced differential equations with deviating argument depending on the unknown function. Panamerican Mathematical Journal 2006,16(1):1–15.