- Research Article
- Open access
- Published:
Bounds of Eigenvalues of 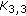 -Minor Free Graphs
-Minor Free Graphs
Journal of Inequalities and Applications volume 2009, Article number: 852406 (2009)
Abstract
The spectral radius  of a graph
of a graph  is the largest eigenvalue of its adjacency matrix. Let
is the largest eigenvalue of its adjacency matrix. Let  be the smallest eigenvalue of
be the smallest eigenvalue of  . In this paper, we have described the
. In this paper, we have described the  -minor free graphs and showed that (A) let
-minor free graphs and showed that (A) let  be a simple graph with order
be a simple graph with order  . If
. If  has no
has no  -minor, then
-minor, then  . (B) Let
. (B) Let  be a simple connected graph with order
be a simple connected graph with order  . If
. If  has no
has no  -minor, then
-minor, then  , where equality holds if and only if
, where equality holds if and only if  is isomorphic to
is isomorphic to  .
.
1. Introduction
In this paper, all graphs are finite undirected graphs without loops and multiple edges. Let  be a graph with
be a graph with  vertices,
vertices,  edges, and minimum degree
edges, and minimum degree  or
or  . The spectral radius
. The spectral radius  of
of  is the largest eigenvalue of its adjacency matrix. Let
is the largest eigenvalue of its adjacency matrix. Let  be the smallest eigenvalue of
be the smallest eigenvalue of  . The join
. The join  is the graph obtained from
is the graph obtained from  by joining each vertex of
by joining each vertex of  to each vertex of
to each vertex of  . A graph
. A graph  is said to be a minor of
is said to be a minor of  if
if  can be obtained from
can be obtained from  by deleting edges, contracting edges, and deleting isolated vertices. A graph
by deleting edges, contracting edges, and deleting isolated vertices. A graph  is
is  -minor free if
-minor free if  has no
has no  -minor.
-minor.
Brualdi and Hoffman [1] showed that the spectral radius satisfies  , where
, where  , with equality if and only if
, with equality if and only if  is isomorphic to the disjoint union of the complete graph
is isomorphic to the disjoint union of the complete graph  and isolated vertices. Stanley [2] improved the above result. Hong et al. [3] showed that if
and isolated vertices. Stanley [2] improved the above result. Hong et al. [3] showed that if  is a simple connected graph then
is a simple connected graph then  with equality if and only if
with equality if and only if  is either a regular graph or a bidegreed graph in which each vertex is of degree either
is either a regular graph or a bidegreed graph in which each vertex is of degree either  or
or  . Hong [4] showed that if
. Hong [4] showed that if  is a
is a  -minor free graph then (1)
-minor free graph then (1)  , where equality holds if and only if
, where equality holds if and only if  is isomorphic to
is isomorphic to  ; (2)
; (2)  , where equality holds if and only if
, where equality holds if and only if  is isomorphic to
is isomorphic to  .
.
In this paper, we have described the  -minor free graphs and obtained that
-minor free graphs and obtained that
(a)let  be a simple graph with order
be a simple graph with order  . If
. If  has no
has no  -minor, then
-minor, then  ;
;
(b)let  be a simple connected graph with order
be a simple connected graph with order  . If
. If  has no
has no  -minor, then
-minor, then  , where equality holds if and only if
, where equality holds if and only if  is isomorphic to
is isomorphic to  .
.
2. 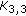 -Minor Free Graphs
-Minor Free Graphs
The intersection  of
of  and
and  is the graph with vertex set
is the graph with vertex set  and edge set
and edge set  . Suppose
. Suppose  is a connected graph and
is a connected graph and  be a minimal separating vertex set of
be a minimal separating vertex set of  . Then we can write
. Then we can write  , where
, where  and
and  are connected and
are connected and  . Now suppose further that
. Now suppose further that  is a complete graph. We say that
is a complete graph. We say that  is a
is a  -sum of
-sum of  and
and  , denoted by
, denoted by  , if
, if  . In particular, let
. In particular, let  denote a
denote a  sum of
sum of  and
and  . Moreover, if
. Moreover, if  or
or  (say
(say  ) has a separating vertex set which induces a complete graph, then we can write
) has a separating vertex set which induces a complete graph, then we can write  such that
such that  and
and  are connected and
are connected and  is a complete subgraph of
is a complete subgraph of  . We proceed like this until none of the resulting subgraphs
. We proceed like this until none of the resulting subgraphs  has a complete separating subgraph. The graphs
has a complete separating subgraph. The graphs  are called the simplical summands of
are called the simplical summands of  . It is easy to show that the subgraphs
. It is easy to show that the subgraphs  are independent of the order in which the decomposition is carried out (see [5]).
are independent of the order in which the decomposition is carried out (see [5]).
Theorem 2.1 (see [6], D. W. Hall; K. Wagner).
A graph has no  -minor if and only if it can be obtained by
-minor if and only if it can be obtained by  -,
-,  -,
-,  -summing starting from planar graphs and
-summing starting from planar graphs and  .
.
A graph  is said to be a edge-maximal
is said to be a edge-maximal  -minor free graph if
-minor free graph if  has no
has no  -minor and
-minor and  has at least an
has at least an  -minor, where
-minor, where  is obtained from
is obtained from  by joining any two nonadjacent vertices of
by joining any two nonadjacent vertices of  . A graph
. A graph  is called a maximal planar graph if the planarity will be not held by joining any two nonadjacent vertices of
is called a maximal planar graph if the planarity will be not held by joining any two nonadjacent vertices of  .
.
Corollary 2.2.
If  is an edge maximal
is an edge maximal  -minor free graph then it can be obtained by
-minor free graph then it can be obtained by  -summing starting from
-summing starting from  and edge maximal planar graphs.
and edge maximal planar graphs.
Proof.
This follows from Theorem 2.1.
Lemma 2.3.
If  and
and  are two maximal planar graphs with order
are two maximal planar graphs with order  and
and  , respectively, then
, respectively, then  is not a maximal planar graph.
is not a maximal planar graph.
Proof.
We denote a planar embedding of  by
by  still. Since
still. Since  is a maximal planar graph, every face boundary in
is a maximal planar graph, every face boundary in  is a 3-cycle. Hence the outside face boundary in
is a 3-cycle. Hence the outside face boundary in  is a 4-cycle, this implies that the graph
is a 4-cycle, this implies that the graph  is not maximal planar.
is not maximal planar.
Further, we have the following results.
Theorem 2.4.
If  is an edge-maximal
is an edge-maximal  -minor free graph with
-minor free graph with  vertices then
vertices then  , where
, where  ,
,  is a maximal planar graph with order
is a maximal planar graph with order  .In particular,
.In particular,
(1)when  , where
, where  ;
;
(2)when  , where
, where  ;
;
(3)when  , where
, where  ;
;
(4)when  is a maximal planar graph.
is a maximal planar graph.
Proof.
Suppose that the graphs  are the simplical summands of
are the simplical summands of  , namely
, namely  . By Corollary 2.2,
. By Corollary 2.2,  is either a maximal planar graph or a
is either a maximal planar graph or a  . By Lemma 2.3, there is at most a maximal planar graph in
. By Lemma 2.3, there is at most a maximal planar graph in  . Hence we have
. Hence we have  , where
, where  ,
,  is a maximal planar graph with order
is a maximal planar graph with order  .
.
Lemma 2.5 (see [7]).
Let  be a simple planar bipartite graph with
be a simple planar bipartite graph with  vertices and
vertices and  edges. Then
edges. Then  .
.
Theorem 2.6.
Let  be a simple connected bipartite graph with
be a simple connected bipartite graph with  vertices and
vertices and  edges. If
edges. If  has no
has no  -minor, then
-minor, then  .
.
Proof.
Let  be a simple connected edge-maximal
be a simple connected edge-maximal  -minor free graph with
-minor free graph with  vertices and
vertices and  edges. Suppose that the graphs
edges. Suppose that the graphs  are the simplical summands of
are the simplical summands of  . Then
. Then  is either a maximal planar graph or the graph
is either a maximal planar graph or the graph  by Corollary 2.2. Further, without loss generality, we may assume that
by Corollary 2.2. Further, without loss generality, we may assume that  is a spanning subgraph of
is a spanning subgraph of  . Let the graph
. Let the graph  be the intersection of
be the intersection of  and
and  . Then
. Then  for
for  . If
. If  then
then  is a subgraph of
is a subgraph of  , implies that
, implies that  . If
. If  is a maximal planar graph then
is a maximal planar graph then  is a simple planar bipartite graph, implies that
is a simple planar bipartite graph, implies that  by Lemma 2.5. Next we prove this result by induction on
by Lemma 2.5. Next we prove this result by induction on  . For
. For  ,
,  . Now we assume it is true for
. Now we assume it is true for  and prove it for
and prove it for  . Let
. Let  and
and  . Then
. Then  by the induction hypothesis.
by the induction hypothesis.

. Hence  .
.
3. Bounds of Eigenvalues of 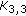 -Minor Free Graphs
-Minor Free Graphs
Lemma 3.1 (see [3]).
If  is a simple connected graph then
is a simple connected graph then  with equality if and only if
with equality if and only if  is either a regular graph or a bidegreed graph in which each vertex is of degree either
is either a regular graph or a bidegreed graph in which each vertex is of degree either  or
or  .
.
Lemma 3.2.
Let  be a simple connected graph with
be a simple connected graph with  vertices and
vertices and  edges. If
edges. If  ,then
,then  , where equality holds if and only if
, where equality holds if and only if  and
and  is either a regular graph or a bidegreed graph in which each vertex is of degree either
is either a regular graph or a bidegreed graph in which each vertex is of degree either  or
or  .
.
Proof.
Because when  and
and  ,
,  is a decreasing function of
is a decreasing function of  for
for  , this follows from Lemma 3.1.
, this follows from Lemma 3.1.
Lemma 3.3.
Let  be a maximal planar graph with order
be a maximal planar graph with order  , and let
, and let  be a graph with
be a graph with  vertices and
vertices and  edges.
edges.
(1)If  and
and  , where
, where  , then
, then  .
.
(2)If  and
and  , where
, where  , then
, then  ,
,  .
.
(3)If  and
and  , where
, where  , then
, then  ,
,  .
.
Proof.
Applying the properties of the maximal planar graphs, this follows by calculating.
Lemma 3.4.
Let  be a maximal planar graph with order
be a maximal planar graph with order  , and let
, and let  be a graph with
be a graph with  vertices.
vertices.
(1)If  and
and  , where
, where  , then
, then  .
.
(2)If  and
and  , where
, where  , then
, then  .
.
(3)If  and
and  , where
, where  , then
, then  .
.
Proof.
It follows that (1) and (3) are true by Lemma 3.2 and 5(1)( 3). Next we prove that (2) is true too.
Let  be a graph obtained from
be a graph obtained from  by expanding
by expanding  (in the simplcal summands of
(in the simplcal summands of  ) to
) to  , such that
, such that  can be obtained by
can be obtained by  -summing
-summing  , namely,
, namely,  .
.
This implies that  by (1). Also we have
by (1). Also we have  , so
, so  .
.
Theorem 3.5.
Let  be a simple graph with order
be a simple graph with order  . If
. If  has no
has no  -minor, then
-minor, then  .
.
Proof.
Since when adding an edge in  the spectral radius
the spectral radius  is strict increasing, we consider the edge-maximal
is strict increasing, we consider the edge-maximal  -minor free graph only. Next we may assume that
-minor free graph only. Next we may assume that  is an edge-maximal
is an edge-maximal  -minor free graph.
-minor free graph.
By Theorem 2.4 and Lemma 3.4, when  ,
,  .
.
When  ,
,  .
.
When  , we have
, we have  by calculating directly, where
by calculating directly, where  ,
,  is a maximal planar graph with order
is a maximal planar graph with order  (see Theorem 2.4).
(see Theorem 2.4).
Therefore when  ,
,  .
.
Remark 3.6.
In Theorem 3.5, the equality holds only if  , for the others, the upper bounds of
, for the others, the upper bounds of  are not sharp. We conjecture that the best bound of
are not sharp. We conjecture that the best bound of  is
is  still.
still.
Lemma 3.7 (see [7]).
If  is a simple connected graph with
is a simple connected graph with  vertices, then there exists a connected bipartite subgraph
vertices, then there exists a connected bipartite subgraph  of
of  such that
such that  with equality holding if and only if
with equality holding if and only if  .
.
Lemma 3.8 (see [7]).
If  is a connected bipartite graph with
is a connected bipartite graph with  vertices and
vertices and  edges, then
edges, then  , where equality holds if and only if
, where equality holds if and only if  is a complete bipartite graph.
is a complete bipartite graph.
Theorem 3.9.
Let  be a simple connected graph with
be a simple connected graph with  vertices. If
vertices. If  has no
has no  -minor, then
-minor, then  , where equality holds if and only if
, where equality holds if and only if  is isomorphic to
is isomorphic to  .
.
Proof.
This follows from Lemmas 3.7, 3.8 and Theorem 2.6.
References
Brualdi RA, Hoffman AJ: On the spectral radius of -matrices. Linear Algebra and Its Applications 1985, 65: 133–146. 10.1016/0024-3795(85)90092-8
Stanley RP: A bound on the spectral radius of graphs with edges. Linear Algebra and Its Applications 1987, 87: 267–269. 10.1016/0024-3795(87)90172-8
Hong Y, Shu J-L, Fang KF: A sharp upper bound of the spectral radius of graphs. Journal of Combinatorial Theory, Series B 2001,81(2):177–183. 10.1006/jctb.2000.1997
Hong Y: Tree-width, clique-minors, and eigenvalues. Discrete Mathematics 2004,274(1–3):281–287.
Thomassen C: Embeddings and minors. In Handbook of Combinatorics, Vol. 1, 2. Edited by: Graham R, Grotschel M, Lovasz L. Elsevier, Amsterdam, The Netherlands; 1995:301–349.
Bondy JA, Murty USR: Graph Theory, Graduate Texts in Mathematics. Volume 244. Springer, New York, NY, USA; 2008:xii+651.
Hong Y, Shu J-L: Sharp lower bounds of the least eigenvalue of planar graphs. Linear Algebra and Its Applications 1999,296(1–3):227–232.
Acknowledgments
The author wishes to express his thanks to the referee for valuable comments which led to an improved version of the paper. Work supported by NNSF of China (no. 10671074) and NSF of Zhejian Province (no. Y7080364).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Fang, KF. Bounds of Eigenvalues of 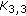 -Minor Free Graphs.
J Inequal Appl 2009, 852406 (2009). https://doi.org/10.1155/2009/852406
-Minor Free Graphs.
J Inequal Appl 2009, 852406 (2009). https://doi.org/10.1155/2009/852406
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/852406
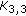 -Minor Free Graphs
-Minor Free Graphs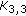 -Minor Free Graphs
-Minor Free Graphs