- Research Article
- Open access
- Published:
Weighted Norm Inequalities for Solutions to the Nonhomogeneous 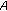 -Harmonic Equation
-Harmonic Equation
Journal of Inequalities and Applications volume 2009, Article number: 851236 (2009)
Abstract
We first prove the local and global two-weight norm inequalities for solutions to the nonhomogeneous  -harmonic equation
-harmonic equation  for differential forms. Then, we obtain some weighed Lipschitz norm and BMO norm inequalities for differential forms satisfying the different nonhomogeneous
for differential forms. Then, we obtain some weighed Lipschitz norm and BMO norm inequalities for differential forms satisfying the different nonhomogeneous  -harmonic equations.
-harmonic equations.
1. Introduction
In the recent years, the  -harmonic equations for differential forms have been widely investigated, see [1], and many interesting and important results have been found, such as some weighted integral inequalities for solutions to the
-harmonic equations for differential forms have been widely investigated, see [1], and many interesting and important results have been found, such as some weighted integral inequalities for solutions to the  -harmonic equations; see [2–7]. Those results are important for studying the theory of differential forms and both qualitative and quantitative properties of the solutions to the different versions of
-harmonic equations; see [2–7]. Those results are important for studying the theory of differential forms and both qualitative and quantitative properties of the solutions to the different versions of  -harmonic equation. In the different versions of
-harmonic equation. In the different versions of  -harmonic equation, the nonhomogeneous
-harmonic equation, the nonhomogeneous  -harmonic equation
-harmonic equation  has received increasing attentions, in [8] Ding has presented some estimates to such equation. In this paper, we extend some estimates that Ding has presented in [8] into the two-weight case. Our results are more general, so they can be used broadly.
has received increasing attentions, in [8] Ding has presented some estimates to such equation. In this paper, we extend some estimates that Ding has presented in [8] into the two-weight case. Our results are more general, so they can be used broadly.
It is well-known that the Lipschitz norm  , where the supremum is over all local cubes
, where the supremum is over all local cubes  , as
, as  is the BMO norm
is the BMO norm  , so the natural limit of the space locLipk(
, so the natural limit of the space locLipk( ) as
) as  is the space BMO(
is the space BMO( ). In Section 3, we establish a relation between these two norms and
). In Section 3, we establish a relation between these two norms and  -norm. We first present the local two-weight Poincaré inequality for
-norm. We first present the local two-weight Poincaré inequality for  -harmonic tensors. Then, as the application of this inequality and the result in [8], we prove some weighted Lipschitz norm inequalities and BMO norm inequalities for differential forms satisfying the different nonhomogeneous
-harmonic tensors. Then, as the application of this inequality and the result in [8], we prove some weighted Lipschitz norm inequalities and BMO norm inequalities for differential forms satisfying the different nonhomogeneous  -harmonic equations. These results can be used to study the basic properties of the solutions to the nonhomogeneous
-harmonic equations. These results can be used to study the basic properties of the solutions to the nonhomogeneous  -harmonic equations.
-harmonic equations.
Now, we first introduce related concepts and notations.
Throughout this paper we assume that  is a bounded connected open subset of
is a bounded connected open subset of  . We assume that
. We assume that  is a ball in
is a ball in  with diameter
with diameter  and
and  is the ball with the same center as
is the ball with the same center as  with
with  . We use
. We use  to denote the Lebesgue measure of
to denote the Lebesgue measure of  . We denote
. We denote  a weight if
a weight if  and
and  a.e.. Also in general
a.e.. Also in general  . For
. For  , we write
, we write  if the weighted
if the weighted  -norm of
-norm of  over
over  satisfies
satisfies  , where
, where  is a real number. A differential
is a real number. A differential  -form
-form  on
on  is a schwartz distribution on
is a schwartz distribution on  with value in
with value in  , we denote the space of differential
, we denote the space of differential  -forms by
-forms by  . We write
. We write  for the
for the  -forms
-forms  with
with  for all ordered
for all ordered  -tuples
-tuples  ,
,  ,
,  . Thus
. Thus  is a Banach space with norm
is a Banach space with norm  . We denote the exterior derivative by
. We denote the exterior derivative by  for
for  . Its formal adjoint operator
. Its formal adjoint operator  is given by
is given by  on
on  ,
,  . A differential
. A differential  -form
-form  is called a closed form if
is called a closed form if  in
in  . Similarly, a differential
. Similarly, a differential  -form
-form  is called a coclosed form if
is called a coclosed form if  . The
. The  -form
-form  is defined by
is defined by  ,
,  and
and  ,
,  , for all
, for all  ,
,  , here
, here  is a homotopy operator, for its definition, see [8].
is a homotopy operator, for its definition, see [8].
Then, we introduce some  -harmonic equations.
-harmonic equations.
In this paper we consider solutions to the nonhomogeneous  -harmonic equation
-harmonic equation

for differential forms, where  and
and  satisfies the following conditions:
satisfies the following conditions:

for almost every  and all
and all  . Here
. Here  is a constant and
is a constant and  is a fixed exponent associated with (1.1) and
is a fixed exponent associated with (1.1) and  . Note that if we choose
. Note that if we choose  in (1.1), then (1.1) will reduce to the conjugate
in (1.1), then (1.1) will reduce to the conjugate  -harmonic equation
-harmonic equation  .
.
Definition 1.1.
We call  and
and  a pair of conjugate
a pair of conjugate  -harmonic tensor in
-harmonic tensor in  if
if  and
and  satisfy the conjugate
satisfy the conjugate  -harmonic equation
-harmonic equation

in  , and
, and  exists in
exists in  , we call
, we call  and
and  conjugate
conjugate  -harmonic tensors in
-harmonic tensors in  .
.
We also consider solutions to the equation of the form

here  and
and  satisfy the conditions:
satisfy the conditions:

for almost every  and all
and all  . Here
. Here  are constants and
are constants and  is a fixed exponent associated with (1.4). A solution to (1.4) is an element of the Sobolev space
is a fixed exponent associated with (1.4). A solution to (1.4) is an element of the Sobolev space  such that
such that

for all  with compact support.
with compact support.
Definition 1.2.
We call  an
an  -harmonic tensor in
-harmonic tensor in  if
if  satisfies the
satisfies the  -harmonic equation (1.4) in
-harmonic equation (1.4) in  .
.
2. The Local and Global 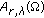 -Weighted Estimates
-Weighted Estimates
In this section, we will extend Lemma 2.3, see in [8], to new version with  weight both locally and globally.
weight both locally and globally.
Definition 2.1.
We say a pair of weights  satisfies the
satisfies the  -condition in a domain
-condition in a domain  and write
and write  for some
for some  and
and  with
with  , if
, if

for any ball  .
.
See [9] for properties of  -weights. We will need the following generalized Hölder's inequality.
-weights. We will need the following generalized Hölder's inequality.
Lemma 2.2.
Let  ,
,  , and
, and  , if
, if  and
and  are measurable functions on
are measurable functions on  , then
, then

for any  .
.
We also need the following lemma; see [8].
Lemma 2.3.
Let  and
and  be a pair of solutions to the nonhomogeneous
be a pair of solutions to the nonhomogeneous  -harmonic equation (1.1) in a domain
-harmonic equation (1.1) in a domain  . If
. If  and
and  , then
, then  if and only if
if and only if  . Moreover, there exist constants
. Moreover, there exist constants  and
and  , independent of
, independent of  and
and  , such that
, such that

for all balls  with
with  .
.
Theorem 2.4.
Let  and
and  be a pair of solutions to the nonhomogeneous
be a pair of solutions to the nonhomogeneous  -harmonic equation (1.1) in a domain
-harmonic equation (1.1) in a domain  . Assume that
. Assume that  for some
for some  and
and  with
with  . Then, there exists a constants
. Then, there exists a constants  , independent of
, independent of  and
and  , such that
, such that

for all balls  with
with  . Here
. Here  is any positive constant with
is any positive constant with  ,
,  , and
, and  . Note that (2.4) can be written as the following symmetric form:
. Note that (2.4) can be written as the following symmetric form:

Proof.
Choose  , since
, since  , using Hölder inequality, we find that
, using Hölder inequality, we find that

Applying the elementary inequality  and Lemma 2.3, we obtain
and Lemma 2.3, we obtain

Choose  , using Hölder inequality with
, using Hölder inequality with  again yields
again yields

Then, choosing  , using Hölder inequality once again, we have
, using Hölder inequality once again, we have

We know that

and hence

Note that

Since

then,

Combining (2.11) and (2.14), we obtain

Using the similar method, we can easily get that

Combining (2.6) and (2.7) gives

Substituting (2.8), (2.15), and (2.16) into (2.17), we have

Since  , then
, then

Putting (2.19) into (2.18), we obtain the desired result

The proof of Theorem 2.4 has been completed.
Using the same method, we have the following two-weighted  -estimate for
-estimate for  .
.
Theorem 2.5.
Let  and
and  be a pair of solutions to the nonhomogeneous
be a pair of solutions to the nonhomogeneous  -harmonic equation (1.1) in a domain
-harmonic equation (1.1) in a domain  . Assume that
. Assume that  for some
for some  and
and  with
with  . Then, there exists a constants
. Then, there exists a constants  , independent of
, independent of  and
and  , such that
, such that

for all balls  with
with  . Here
. Here  is any positive constant with
is any positive constant with  ,
,  , and
, and  .
.
It is easy to see that the inequality (2.21) is equivalent to

As applications of the local results, we prove the following global norm comparison theorem.
Lemma 2.6.
Each  has a modified Whitney cover of cubes
has a modified Whitney cover of cubes  such that
such that

for all  and some
and some  and if
and if  , then there exists a cube
, then there exists a cube  (this cube does not need be a member of
(this cube does not need be a member of  ) in
) in  such that
such that  .
.
Theorem 2.7.
Let  and
and  be a pair of solutions to the nonhomogeneous
be a pair of solutions to the nonhomogeneous  -harmonic equation (1.1) in a bounded domain
-harmonic equation (1.1) in a bounded domain  . Assume that
. Assume that  for some
for some  and
and  with
with  . Then, there exist constants
. Then, there exist constants  and
and  , independent of
, independent of  and
and  , such that
, such that

Here  is any positive constant with
is any positive constant with  ,
,  ,
,  , and
, and

for  and
and  .
.
Proof.
Applying Theorem 2.4 and Lemma 2.6, we have

Since  is bounded. The proof of inequality (2.24) has been completed. Similarly, using Theorem 2.5 and Lemma 2.6, inequality (2.25) can be proved immediately. This ends the proof of Theorem 2.7.
is bounded. The proof of inequality (2.24) has been completed. Similarly, using Theorem 2.5 and Lemma 2.6, inequality (2.25) can be proved immediately. This ends the proof of Theorem 2.7.
Definition 2.8.
We say the weight  satisfies the
satisfies the  -condition in a domain
-condition in a domain  write
write  for some
for some  with
with  , if
, if

for any ball  .
.
We see that  -weight reduce to the usual
-weight reduce to the usual  -weight if
-weight if  and
and  ; see [10].
; see [10].
And, if  and
and  in Theorem 2.7, it is easy to obtain Theorems
in Theorem 2.7, it is easy to obtain Theorems  and
and  in [8].
in [8].
3. Estimates for Lipschitz Norms and BMO Norms
In [11] Ding has presented some estimates for the Lipchitz norms and BMO norms. In this section, we will prove another estimates for the Lipchitz norms and BMO norms.
Definition 3.1.
Let  ,
,  . We write
. We write  ,
,  , if
, if

for some  .
.
Similarly, we write  BMO
BMO if
if

for some  . When
. When  is a
is a  -form, (3.2) reduces to the classical definition of BMO
-form, (3.2) reduces to the classical definition of BMO .
.
We also discuss the weighted Lipschitz and BMO norms.
Definition 3.2.
Let  ,
,  . We write
. We write  ,
,  , if
, if

Similarly, for  ,
,  . We write
. We write  BMO
BMO , if
, if

for some  , where
, where  is a bounded domain, the measure
is a bounded domain, the measure  is defined by
is defined by  ,
,  is a weight, and
is a weight, and  is a real number.
is a real number.
We need the following classical Poincaré inequality; see [10].
Lemma 3.3.
Let  and
and  , then
, then  is in
is in  with
with  and
and

We also need the following lemma; see [2].
Lemma 3.4.
Suppose that  is a solution to (1.4),
is a solution to (1.4),  and
and  . There exists a constant
. There exists a constant  , depending only on
, depending only on  ,
,  ,
,  ,
,  ,
,  , and
, and  , such that
, such that

for all balls  with
with  .
.
We need the following local weighted Poincaré inequality for  -harmonic tensors.
-harmonic tensors.
Theorem 3.5.
Let  be an
be an  -harmonic tensor in a domain
-harmonic tensor in a domain  and
and  ,
,  . Assume that
. Assume that  ,
,  , and
, and  for some
for some  and
and  with
with  . Then, there exists a constant
. Then, there exists a constant  , independent of
, independent of  , such that
, such that

for all balls  with
with  . Here
. Here  is any constant with
is any constant with  .
.
Proof.
Choose  , since
, since  , using Hölder inequality, we find that
, using Hölder inequality, we find that

Taking  , then
, then  , using Lemmas 3.4 and 3.3 and the same method as [2, Proof of Theorem
, using Lemmas 3.4 and 3.3 and the same method as [2, Proof of Theorem  ], we obtain
], we obtain

where  . Using Hölder inequality with
. Using Hölder inequality with  again yields
again yields

Substituting (3.10) in (3.9), we have

Since  , then
, then

Combining (3.11) and (3.12) gives

Note that

Finally, we obtain the desired result

This ends the proof of Theorem 3.5.
Similarly, if setting  and
and  in Theorem 3.5, we obtain Theorem
in Theorem 3.5, we obtain Theorem  in [2]. And we choose
in [2]. And we choose  in Theorem 3.5, we have the classical Poincaré inequality (3.5).
in Theorem 3.5, we have the classical Poincaré inequality (3.5).
Lemma 3.6 (see [8]).
Let  and
and  be a pair of solution to the conjugate
be a pair of solution to the conjugate  -harmonic tensor in
-harmonic tensor in  . Assume
. Assume  for some
for some  . Then, there exists a constant
. Then, there exists a constant  , independent of
, independent of  , such that
, such that

Here  is any positive constant with
is any positive constant with  ,
,  and
and  .
.
Theorem 3.7.
Let  be an
be an  -harmonic tensor in a domain
-harmonic tensor in a domain  , and all
, and all  with
with  , and
, and  ,
,  . Assume that
. Assume that  and
and  for some
for some  and
and  with
with  for any
for any  . Then, there exist constants
. Then, there exist constants  and
and  , independent of
, independent of  , such that
, such that


where  and
and  are constants with
are constants with  and
and 
Proof.
We note that  implies that
implies that

for any ball  . Using (3.7) and the Hölder inequality with
. Using (3.7) and the Hölder inequality with  , we have
, we have

From the definition of the Lipschitz norm (3.3), (3.19), and (3.20), we obtain

Since  and
and  . The desired result for Lipschitz norm has been completed.
. The desired result for Lipschitz norm has been completed.
Then, we prove the theorem for BMO norm

From (3.21) we find

Using (3.17) we have

Now, we have completed the proof of Theorem 3.7.
Similarly, if setting  and
and  in Theorem 3.7, we obtain the following theorem.
in Theorem 3.7, we obtain the following theorem.
Theorem 3.8.
Let  be an
be an  -harmonic tensor in a domain
-harmonic tensor in a domain  , and all
, and all  with
with  , and
, and  ,
,  . Assume that
. Assume that  and
and  for
for  with
with  for any
for any  . Then, there exist constants
. Then, there exist constants  and
and  , independent of
, independent of  , such that
, such that


where  and
and  are constants with
are constants with  and
and 
If  , we have
, we have

Using Lemma 3.6, we can also obtain the following theorem.
Theorem 3.9.
Let  and
and  be a pair of conjugate
be a pair of conjugate  -harmonic tensor in a domain
-harmonic tensor in a domain  , then
, then  if and only if
if and only if  where the measure
where the measure  is defined by
is defined by  , and all
, and all  with
with  . Assume that
. Assume that  for
for  with
with  for any
for any  . Then, there exist constants
. Then, there exist constants  and
and  , independent of
, independent of  and
and  , such that
, such that

where  and
and  are positive constants with
are positive constants with  and
and  , for
, for  ,
, 
Proof.
From (3.25), we have

Choose  ,
,  , using Lemma 3.6, it is easy to obtain the desire result
, using Lemma 3.6, it is easy to obtain the desire result

Using the similar method for BMO norm, we have

If  , we have
, we have

References
Agarwal RP, Ding S: Advances in differential forms and the -harmonic equation. Mathematical and Computer Modelling 2003,37(12–13):1393–1426. 10.1016/S0895-7177(03)90049-5
Ding S, Nolder CA: Weighted Poincaré inequalities for solutions to -harmonic equations. Illinois Journal of Mathematics 2002,46(1):199–205.
Liu B: -weighted Caccioppoli-type and Poincaré-type inequalities for -harmonic tensors. International Journal of Mathematics and Mathematical Sciences 2002,31(2):115–122. 10.1155/S0161171202107046
Xing Y: Weighted Poincaré-type estimates for conjugate -harmonic tensors. Journal of Inequalities and Applications 2005, (1):1–6.
Yuming X: Weighted integral inequalities for solutions of the -harmonic equation. Journal of Mathematical Analysis and Applications 2003,279(1):350–363. 10.1016/S0022-247X(03)00036-2
Ding S, Ling Y: Weighted norm inequalities for conjugate -harmonic tensors. Journal of Mathematical Analysis and Applications 1996,203(1):278–288. 10.1006/jmaa.1996.0380
Ding S, Shi P: Weighted Poincaré-type inequalities for differential forms in -averaging domains. Journal of Mathematical Analysis and Applications 1998,227(1):200–215. 10.1006/jmaa.1998.6096
Ding S: Local and global norm comparison theorems for solutions to the nonhomogeneous -harmonic equation. Journal of Mathematical Analysis and Applications 2007,335(2):1274–1293. 10.1016/j.jmaa.2007.02.048
Neugebauer CJ: Inserting -weights. Proceedings of the American Mathematical Society 1983,87(4):644–648.
Ding S: Two-weight Caccioppoli inequalities for solutions of nonhomogeneous -harmonic equations on Riemannian manifolds. Proceedings of the American Mathematical Society 2004,132(8):2367–2375. 10.1090/S0002-9939-04-07347-2
Ding S: Lipschitz and BOM norm inequalities for operators. Proceedings of the 5th World Congress of Nonliner Analysis, July 2008, Orlando Fla, USA
Acknowledgment
This work was supported by Science Research Foundation in Harbin Institute of Technology (HITC200709) and Development Program for Outstanding Young Teachers in HIT (HITQNJS.2006.052).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wen, H. Weighted Norm Inequalities for Solutions to the Nonhomogeneous 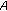 -Harmonic Equation.
J Inequal Appl 2009, 851236 (2009). https://doi.org/10.1155/2009/851236
-Harmonic Equation.
J Inequal Appl 2009, 851236 (2009). https://doi.org/10.1155/2009/851236
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/851236
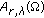 -Weighted Estimates
-Weighted Estimates