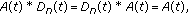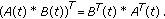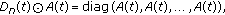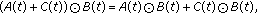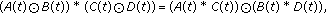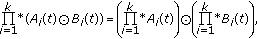- Research Article
- Open access
- Published:
On the Connection between Kronecker and Hadamard Convolution Products of Matrices and Some Applications
Journal of Inequalities and Applications volume 2009, Article number: 736243 (2009)
Abstract
We are concerned with Kronecker and Hadamard convolution products and present some important connections between these two products. Further we establish some attractive inequalities for Hadamard convolution product. It is also proved that the results can be extended to the finite number of matrices, and some basic properties of matrix convolution products are also derived.
1. Introduction
There has been renewed interest in the Convolution Product of matrix functions that is very useful in some applications; see for example [1–6]. The importance of this product stems from the fact that it arises naturally in divers areas of mathematics. In fact, the convolution product plays very important role in system theory, control theory, stability theory, and, other fields of pure and applied mathematics. Further the technique has been successfully applied in various fields of matrix algebra such as, in matrix equations, matrix differential equations, matrix inequalities, and many other subjects; for details see [1, 7, 8]. For example, in [2], Nikolaos established some inequalities involving convolution product of matrices and presented a new method to obtain closed form solutions of transition probabilities and dependability measures and then solved the renewal matrix equation by using the convolution product of matrices. In [6], Sumita established the matrix Laguerre transform to calculate matrix convolutions and evaluated a matrix renewal function, similarly, in [9], Boshnakov showed that the entries of the autocovariances matrix function can be expressed in terms of the Kronecker convolution product. Recently in [1], Kiliçman and Al Zhour presented the iterative solution of such coupled matrix equations based on the Kronecker convolution structures.
In this paper, we consider Kronecker and Hadamard convolution products for matrices and define the so-called Dirac identity matrix  which behaves like a group identity element under the convolution matrix operation. Further, we present some results which includes matrix equalities as well as inequalities related to these products and give attractive application to the inequalities that involves Hadamard convolution product. Some special cases of this application are also considered. First of all, we need the following notations. The notation
which behaves like a group identity element under the convolution matrix operation. Further, we present some results which includes matrix equalities as well as inequalities related to these products and give attractive application to the inequalities that involves Hadamard convolution product. Some special cases of this application are also considered. First of all, we need the following notations. The notation  is the set of all
is the set of all  absolutely integrable matrices for all
absolutely integrable matrices for all  , and if
, and if  , we write
, we write  instead of
instead of  . The notation
. The notation  is the transpose of matrix function
is the transpose of matrix function  . The notations
. The notations  and
and  are the Dirac delta function and Dirac identity matrix, respectively; here, the notation
are the Dirac delta function and Dirac identity matrix, respectively; here, the notation  is the scalar identity matrix of order
is the scalar identity matrix of order  . The notations
. The notations  ,
,  , and
, and  are convolution product, Kronecker convolution product and Hadamard convolution product of matrix functions
are convolution product, Kronecker convolution product and Hadamard convolution product of matrix functions  and
and  , respectively.
, respectively.
2. Matrix Convolution Products and Some Properties
In this section, we introduce Kronecker and Hadamard convolution products of matrices, obtain some new results, and establish connections between these products that will be useful in some applications.
Definition 2.1.
Let  ,
,  , and
, and  . The convolution, Kronecker convolution and Hadamard convolution products are matrix functions defined for
. The convolution, Kronecker convolution and Hadamard convolution products are matrix functions defined for  as follows (whenever the integral is defined).
as follows (whenever the integral is defined).
(i)Convolution product

(ii)Kronecker convolution product

(iii)Hadamard convolution product

where  is the
is the  th submatrix of order
th submatrix of order  ; thus
; thus  is of order
is of order  ,
,  is of order
is of order  , and similarly, the product
, and similarly, the product  is of order
is of order  .
.
The following two theorems are easily proved by using the definition of the convolution product and Kronecker product of matrices, respectively.
Theorem 2.2.
Let  ,
,  ,
,  , and let
, and let  . Then for scalars
. Then for scalars  and
and 
-
(i)
 (2.4)
(2.4)
-
(ii)
 (2.5)
(2.5)
-
(iii)
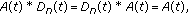 (2.6)
(2.6)
-
(iv)
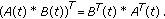 (2.7)
(2.7)
Theorem 2.3.
Let  ,
,  and let
and let  . Then
. Then
-
(i)
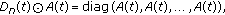 (2.8)
(2.8)
-
(ii)
 (2.9)
(2.9)
-
(iii)
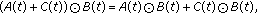 (2.10)
(2.10)
-
(iv)
 (2.11)
(2.11)
-
(v)
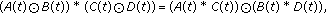 (2.12)
(2.12)
-
(vi)
 (2.13)
(2.13)
The above results can easily be extended to the finite number of matrices as in the following corollary.
Corollary 2.4.
Let  and
and 
 be matrices. Then
be matrices. Then
-
(i)
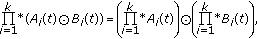 (2.14)
(2.14)
-
(ii)
 (2.15)
(2.15)
Proof.
(i) The proof is a consequence of Theorem 2.3(v). Now we can proceed by induction on  . Assume that Corollary 2.4 holds for products of
. Assume that Corollary 2.4 holds for products of  matrices. Then
matrices. Then

Similarly we can prove (ii).
Theorem 2.5.
Let  , and let
, and let  . Then
. Then

Here,  and
and  of order
of order  ,
,  is the
is the  th column of Dirac identity matrix
th column of Dirac identity matrix  with property
with property  . In particular, if
. In particular, if  , then we have
, then we have

Proof.
Compute

This completes the proof of Theorem 2.5.
Corollary 2.6.
Let 
 . Then there exist two matrices
. Then there exist two matrices  of order
of order  and
and  of order
of order  such that
such that

where

is of order  ,
,  is an
is an  matrix with all entries equal to zero,
matrix with all entries equal to zero,  is an
is an  matrix of zeros except for a
matrix of zeros except for a  in the
in the  th position, and there are
th position, and there are  zero matrices
zero matrices  between
between  and
and  (
( ). In particular, if
). In particular, if  , then we have
, then we have

Proof.
The proof is by induction on  . If
. If  , then the result is true by using (2.17). Now suppose that corollary holds for the Hadamard convolution product of
, then the result is true by using (2.17). Now suppose that corollary holds for the Hadamard convolution product of  matrices. Then we have
matrices. Then we have

which is based on the fact that

and thus the inductive step is completed.
Corollary 2.7.
Let  and
and  be a matrix of zeros and
be a matrix of zeros and  that satisfies the (2.17). Then
that satisfies the (2.17). Then  and
and  is a diagonal
is a diagonal  matrix of zeros, and then the following inequality satisfied
matrix of zeros, and then the following inequality satisfied

Proof.
It follows immediately by the definition of matrix  .
.
Theorem 2.8.
Let  and
and  . Then for any
. Then for any  matrix
matrix  ,
,

Proof.
By Corollary 2.7, it is clear that  and so
and so

This completes the proof of Theorem 2.8.
We note that Hadamard convolution product differs from the convolution product of matrices in many ways. One important difference is the commutativity of Hadamard convolution multiplication

Similarly, the diagonal matrix function can be formed by using Hadamard convolution multiplication with Dirac identity matrix. For example, if  ,
,  and
and  Dirac identity then we have
Dirac identity then we have
(i) if and only if
if and only if  and
and  are both diagonal matrices;
are both diagonal matrices;
(ii) .
.
3. Some New Applications
Now based on inequality (2.26) in the previous section we can easily make some different inequalities on using the commutativity of Hadamard convolution product. Thus we have the following theorem.
Theorem 3.1.
For matrices  and
and  and for
and for  , we have
, we have 

In particular, if  , then we have
, then we have

Proof.
Choose  , where
, where  , and
, and  and
and  are real scalars not both zero. Since
are real scalars not both zero. Since

on using Theorem 2.5 we can easily obtain that

Now one can also easily show that

By setting  , then it follows that
, then it follows that  ; further the arithmetic-geometric mean inequality ensures that
; further the arithmetic-geometric mean inequality ensures that  and the choices
and the choices  and
and  thus
thus  takes all values in
takes all values in  . Now by using (3.4), (3.5) and inequality (2.26) we can establish Theorem 3.1.
. Now by using (3.4), (3.5) and inequality (2.26) we can establish Theorem 3.1.
Further, Theorem 3.1 can be extended to the case of Hadamard convolution products which involves finite number of matrices as follows.
Theorem 3.2.
Let 
 . Then for real scalars
. Then for real scalars  , which are not all zero
, which are not all zero

where  and
and  with
with  .
.
Proof.
Let

By taking indices " " and using (2.20) of Corollary 2.6 follows that
" and using (2.20) of Corollary 2.6 follows that

Now on using Corollary 2.6 and the commutativity of Hadamard convolution product yields

where  and
and  with
with  then
then

Thus it follows that

Now by applying inequality (2.26), and (3.6) and (3.7) thus we establish Theorem 3.2.
We note that many special cases can be derived from Theorem 3.2. For example, in order to see that inequality (3.6) is an extension of inequality (3.2) we set  and
and  . Next, we recover inequality (3.1) of Theorem 3.1, by letting
. Next, we recover inequality (3.1) of Theorem 3.1, by letting  , then
, then  with
with  , that is,
, that is,  then we have
then we have

By simplification we have

for every  , just as required. Finally, if we let
, just as required. Finally, if we let  ,
,  , and
, and  , then on using Theorem 3.2 we have an attractive inequality as follows.
, then on using Theorem 3.2 we have an attractive inequality as follows.

References
Kiliçman A, Al Zhour Z: Iterative solutions of coupled matrix convolution equations. Soochow Journal of Mathematics 2007,33(1):167–180.
Limnios N: Dependability analysis of semi-Markov systems. Reliability Engineering and System Safety 1997,55(3):203–207. 10.1016/S0951-8320(96)00121-4
Saitoh S: New norm type inequalities for linear mappings. Journal of Inequalities in Pure and Applied Mathematics 2003,4(3, article 57):1–5.
Saitoh S, Tuan VK, Yamamoto M: Convolution inequalities and applications. Journal of Inequalities in Pure and Applied Mathematics 2003,4(3, article 50):1–8.
Saitoh S, Tuan VK, Yamamoto M: Reverse weighted -norm inequalities in convolutions. Journal of Inequalities in Pure and Applied Mathematics 2000,1(1, article 7):1–7.
Sumita U: The matrix Laguerre transform. Applied Mathematics and Computation 1984,15(1):1–28. 10.1016/0096-3003(84)90050-X
Al Zhour Z, Kiliçman A: Some new connections between matrix products for partitioned and non-partitioned matrices. Computers & Mathematics with Applications 2007,54(6):763–784. 10.1016/j.camwa.2006.12.045
Kiliçman A, Al Zhour Z: The general common exact solutions of coupled linear matrix and matrix differential equations. Journal of Analysis and Computation 2005,1(1):15–29.
Boshnakov GN: The asymptotic covariance matrix of the multivariate serial correlations. Stochastic Processes and Their Applications 1996,65(2):251–258. 10.1016/S0304-4149(96)00104-4
Acknowledgments
The authors gratefully acknowledge that this research partially supported by Ministry of Science, Technology and Innovations(MOSTI), Malaysia under the Grant IRPA project, no: 09-02-04-0898-EA001. The authors also would like to express their sincere thanks to the referees for their very constructive comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kılıçman, A., Al Zhour, Z. On the Connection between Kronecker and Hadamard Convolution Products of Matrices and Some Applications. J Inequal Appl 2009, 736243 (2009). https://doi.org/10.1155/2009/736243
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/736243