- Research Article
- Open access
- Published:
Inequalities for Single Crystal Tube Growth by Edge-Defined Film-Fed Growth Technique
Journal of Inequalities and Applications volume 2009, Article number: 732106 (2009)
Abstract
The axi-symmetric Young-Laplace differential equation is analyzed. Solutions of this equation can describe the outer or inner free surface of a static meniscus (the static liquid bridge free surface between the shaper and the crystal surface) occurring in single crystal tube growth. The analysis concerns the dependence of solutions of the equation on a parameter  which represents the controllable part of the pressure difference across the free surface. Inequalities are established for
which represents the controllable part of the pressure difference across the free surface. Inequalities are established for  which are necessary or sufficient conditions for the existence of solutions which represent a stable and convex outer or inner free surfaces of a static meniscus. The analysis is numerically illustrated for the static menisci occurring in silicon tube growth by edge-defined film-fed growth (EFGs) technique. This kind of inequalities permits the adequate choice of the process parameter
which are necessary or sufficient conditions for the existence of solutions which represent a stable and convex outer or inner free surfaces of a static meniscus. The analysis is numerically illustrated for the static menisci occurring in silicon tube growth by edge-defined film-fed growth (EFGs) technique. This kind of inequalities permits the adequate choice of the process parameter  . With this aim this study was undertaken.
. With this aim this study was undertaken.
1. Introduction
The first successful Si tube growth was reported in [1]. Also a theory of tube growth by E.F.G. process is developed there to show the dependence of the tube wall thickness on the growth variables. The theory concerns the calculation of the shape of the liquid-vapor interface (i.e., the free surface of the meniscus) and of the heat flow in the system. The inner and the outer free surface shapes of the meniscus (Figure 1) were calculated from Young-Laplace capillary equation, in which the pressure difference  across a point on the free surface is considered to be
across a point on the free surface is considered to be  constant, where
constant, where  represents the effective height of the growth interface (Figure 1). The above approximation of
represents the effective height of the growth interface (Figure 1). The above approximation of  is valid when
is valid when  , where
, where  is the height of the growth interface above the shaper top. Another approximation used in [1] is that the outer and inner free surface shapes are approximated by circular segments. With these relatively tight tolerances concerning the menisci in conjunction with the heat flow calculation in the system, the predictive model developed in [1] has been shown to be useful tool understanding the feasible limits of the wall thickness control. A more accurate predictive model would require an increase of the acceptable tolerance range introduced by approximation.
is the height of the growth interface above the shaper top. Another approximation used in [1] is that the outer and inner free surface shapes are approximated by circular segments. With these relatively tight tolerances concerning the menisci in conjunction with the heat flow calculation in the system, the predictive model developed in [1] has been shown to be useful tool understanding the feasible limits of the wall thickness control. A more accurate predictive model would require an increase of the acceptable tolerance range introduced by approximation.
The growth process was scaled up by Kaljes et al. in [2] to grow 15 cm diameter silicon tubes. It has been realized that theoretical investigations are necessary for the improvement of the technology. Since the growth system consists of a small die type (1 mm width) and a thin tube (order of  m wall thickness), the width of the melt/solid interface and the meniscus are accordingly very small. Therefore, it is essential to obtain accurate solution for the free surface of the meniscus, the temperature, and the liquid-crystal interface position in this tinny region.
m wall thickness), the width of the melt/solid interface and the meniscus are accordingly very small. Therefore, it is essential to obtain accurate solution for the free surface of the meniscus, the temperature, and the liquid-crystal interface position in this tinny region.
For single crystal tube growth by edge-defined film-fed growth (E.F.G.) technique, in hydrostatic approximation the free surface of a static meniscus is described by the Young-Laplace capillary equation [3]:

Here  is the melt surface tension,
is the melt surface tension,  denotes the melt density,
denotes the melt density,  is the gravity acceleration,
is the gravity acceleration,  denote the main normal curvatures of the free surface at a point
denote the main normal curvatures of the free surface at a point  of the free surface,
of the free surface,  is the coordinate of
is the coordinate of  with respect to the
with respect to the  axis, directed vertically upwards, and
axis, directed vertically upwards, and  is the pressure difference across the free surface. For the outer free surface,
is the pressure difference across the free surface. For the outer free surface,  and for the inner free surface,
and for the inner free surface,  .
.
Here  denotes the hydrodynamic pressure in the meniscus melt,
denotes the hydrodynamic pressure in the meniscus melt,  denote the pressure of the gas flow introduced in the furnace in order to release the heat from the outer and inner walls of the tube, respectively, and
denote the pressure of the gas flow introduced in the furnace in order to release the heat from the outer and inner walls of the tube, respectively, and  denotes the melt column height between the horizontal crucible melt level and the shaper top level. When the shaper top level is above the crucible melt level, then
denotes the melt column height between the horizontal crucible melt level and the shaper top level. When the shaper top level is above the crucible melt level, then  , and when the crucible melt level is above the shaper top level, then
, and when the crucible melt level is above the shaper top level, then  (see Figure 1).
(see Figure 1).
To calculate the outer and inner free surface shapes of the static meniscus, it is convenient to employ the Young-Laplace (1.1) in its differential form. This form of the (1.1) can be obtained as a necessary condition for the minimum of the free energy of the melt column [3].
For the growth of a single crystal tube of inner radius  and outer radius
and outer radius  the axi-symmetric differential equation of the outer free surface is given by
the axi-symmetric differential equation of the outer free surface is given by

which is the Euler equation for the energy functional

The axi-symmetric differential equation of the inner free surface is given by

which is the Euler equation for the energy functional

The state of the arts at the time 1993-1994, concerning the dependence of the shape of the meniscus free surface on the pressure difference  for small and large bond numbers, in the case of the growth of single crystal rods by E.F.G. technique, are summarized in [4]. According to [4], for the general differential equation (1.2), (1.4) describing the free surface of a liquid meniscus, there are no complete analysis and solution. For the general equation only numerical integrations were carried out for a number of process parameter values that were of practical interest at the moment.
for small and large bond numbers, in the case of the growth of single crystal rods by E.F.G. technique, are summarized in [4]. According to [4], for the general differential equation (1.2), (1.4) describing the free surface of a liquid meniscus, there are no complete analysis and solution. For the general equation only numerical integrations were carried out for a number of process parameter values that were of practical interest at the moment.
Later, in 2001, Rossolenko shows in [5] that the hydrodynamic factor is too small to be considered in the automated single crystal tube growth. Finally, in [6] the authors present theoretical and numerical study of meniscus dynamics under axi-symmetric and asymmetric configurations. In [6] the meniscus free surface is approximated by an arc of constant curvature, and a meniscus dynamics model is developed to consider meniscus shape and its dynamics, heat and mass transfer around the die-top and meniscus. Analysis reveals the correlations among tube wall thickness, effective melt height, pull-rate, die-top temperature, and crystal environmental temperature.
In the present paper the shape of the inner and outer free surfaces of the static meniscus is analyzed as function of  , the controllable part of the pressure difference across the free surface, and the static stability of the free surfaces is investigated. The novelty with respect to the considerations presented in literature consists in the fact that the free surface is not approximated as in [1, 6], by an arc with constant curvature, and the pressure of the gas flow introduced in the furnace for releasing the heat from the tube wall is taken in consideration. The setting of the thermal conditions is not considered in this paper.
, the controllable part of the pressure difference across the free surface, and the static stability of the free surfaces is investigated. The novelty with respect to the considerations presented in literature consists in the fact that the free surface is not approximated as in [1, 6], by an arc with constant curvature, and the pressure of the gas flow introduced in the furnace for releasing the heat from the tube wall is taken in consideration. The setting of the thermal conditions is not considered in this paper.
2. Meniscus Outer Free Surface Shape Analysis in the Case of Tube Growth
Consider the differential equation

and  such that
such that  .
.
Definition 2.1.
A solution  of the (2.1) describes the outer free surface of a static meniscus on the interval
of the (2.1) describes the outer free surface of a static meniscus on the interval  if possesses the following properties:
if possesses the following properties:
-
(a)
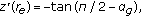
-
(b)
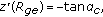 and
and -
(c)
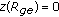 and
and 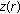 is strictly decreasing on
is strictly decreasing on 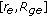 .
.
The described outer free surface is convex on  if in addition the following inequality holds:
if in addition the following inequality holds:
-
(d)
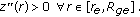
Theorem 2.2.
If there exists a solution of (2.1), which describes a convex outer free surface of a static meniscus on the closed interval  , then the following inequalities hold:
, then the following inequalities hold:

Proof.
Let  be a solution of (2.1), which describes a convex outer free surface of a static meniscus on the closed interval
be a solution of (2.1), which describes a convex outer free surface of a static meniscus on the closed interval  and
and  . The function
. The function  verifies the equation
verifies the equation

and the boundary conditions

Hence, there exists  such that the following equality holds:
such that the following equality holds:

Since  ,
,  is strictly increasing and
is strictly increasing and  is strictly decreasing on
is strictly decreasing on  , therefore the values of
, therefore the values of  are in the range
are in the range  and the following inequalities hold:
and the following inequalities hold:

Equality (2.5) and inequalities (2.6) imply inequalities (2.2).
Corollary 2.3.
If  with
with  , then inequalities (2.2) become
, then inequalities (2.2) become

Corollary 2.4.
If  , then
, then  and (2.7) becomes
and (2.7) becomes

If  , then
, then  and
and  .
.
Theorem 2.5.
Let  be such that
be such that  . If
. If  satisfies the inequality
satisfies the inequality

then there exists  in the closed interval
in the closed interval  such that the solution of the initial value problem
such that the solution of the initial value problem

on the interval  describes the convex outer free surface of a static meniscus.
describes the convex outer free surface of a static meniscus.
Proof.
Consider the solution  of the initial value problem (2.10). Denote by
of the initial value problem (2.10). Denote by  the maximal interval on which the function
the maximal interval on which the function  exists and by
exists and by  the function
the function  defined on
defined on  . Remark that for
. Remark that for  the equality (2.3) holds.
the equality (2.3) holds.
Since

there exists  ,
,  such that for any
such that for any  the following inequalities hold:
the following inequalities hold:

Let  be defined by
be defined by

It is clear that  and for any
and for any  inequalities (2.12) hold.
inequalities (2.12) hold.
From (2.12) and (2.13) it follows that  is strictly increasing and bounded on
is strictly increasing and bounded on  Therefore
Therefore  exists and satisfies
exists and satisfies

Moreover, since  is strictly decreasing and possesses bounded derivative on
is strictly decreasing and possesses bounded derivative on  ,
,  exists too, it is finite, and satisfies
exists too, it is finite, and satisfies

We will show now that  and
and  . In order to show that
. In order to show that  we assume the contrary, that is, that
we assume the contrary, that is, that  . Under this hypothesis we have
. Under this hypothesis we have

for some  . Hence
. Hence  This last inequality is impossible, since according to the inequality (2.14), we have
This last inequality is impossible, since according to the inequality (2.14), we have  . Therefore,
. Therefore,  , defined by (2.14), satisfies
, defined by (2.14), satisfies  .
.
In order to show that  we remark that from the definition (2.14) of
we remark that from the definition (2.14) of  it follows that at least one of the following three equalities holds:
it follows that at least one of the following three equalities holds:

Since  for any
for any  it follows that the equality
it follows that the equality  is impossible. Hence, we obtain that at
is impossible. Hence, we obtain that at  at least one of the following two equalities holds:
at least one of the following two equalities holds:  ,
,  . We show now that the equality
. We show now that the equality  is impossible. For that we assume the contrary, that is,
is impossible. For that we assume the contrary, that is,  . Under this hypothesis, from (2.12) we have:
. Under this hypothesis, from (2.12) we have:

what is impossible.
In this way we obtain that the equality  holds.
holds.
For  the solution of the initial value problem (2.8) on the interval
the solution of the initial value problem (2.8) on the interval  describes a convex outer free surface of a static meniscus.
describes a convex outer free surface of a static meniscus.
Corollary 2.6.
If for  the following inequality holds:
the following inequality holds:

then there exists  in the interval
in the interval  such that the solution of the initial value problem (2.10) on the interval
such that the solution of the initial value problem (2.10) on the interval  describes a convex outer free surface of a static meniscus.
describes a convex outer free surface of a static meniscus.
Corollary 2.7.
If for  the following inequalities hold:
the following inequalities hold:

then there exists  in the interval
in the interval  such that the solution of the initial value problem (2.10) on the interval
such that the solution of the initial value problem (2.10) on the interval  describes a convex outer free surface of a static meniscus. The existence of
describes a convex outer free surface of a static meniscus. The existence of  and the inequality
and the inequality  follows from Theorem 2.5. The inequality
follows from Theorem 2.5. The inequality  follows from Corollary 2.3.
follows from Corollary 2.3.
Remark 2.8.
The solution of the initial value problem (2.10) is convex at  (i.e.,
(i.e.,  ) if and only if
) if and only if

That is because  if and only if
if and only if  , that is,
, that is,

Moreover, if  , the solution
, the solution  of the initial value problem (2.8) is convex everywhere (i.e.,
of the initial value problem (2.8) is convex everywhere (i.e.,  for
for  ). That is because the change of convexity implies the existence of
). That is because the change of convexity implies the existence of  such that
such that  and
and  , what is impossible.
, what is impossible.
Theorem 2.9.
If a solution  of (2.1) describes a convex outer free surface of a static meniscus on the interval
of (2.1) describes a convex outer free surface of a static meniscus on the interval  , then it is a weak minimum for the energy functional of the melt column:
, then it is a weak minimum for the energy functional of the melt column:

Proof.
Since (2.1) is the Euler equation for (2.23), it is sufficient to prove that the Legendre and Jacobi conditions are satisfied in this case.
Denote by  the function defined as
the function defined as

It is easy to verify that we have

Hence, the Legendre condition is satisfied.
The Jacobi equation

in this case is given by

For (2.27) the following inequalities hold:

Hence, the equation

is a Sturm type upper bound for (2.27) [7].
Since every nonzero solution of (2.29) vanishes at most once on the interval  , the solution
, the solution  of the initial value problem
of the initial value problem

has only one zero on the interval  [7]. Hence the Jacobi condition is satisfied.
[7]. Hence the Jacobi condition is satisfied.
Definition 2.10.
A solution  of (2.1) which describes the outer free surface of a static meniscus is said to be stable if it is a weak minimum of the energy functional of the melt column.
of (2.1) which describes the outer free surface of a static meniscus is said to be stable if it is a weak minimum of the energy functional of the melt column.
Remark 2.11.
Theorem 2.9 shows that if  describes a convex outer free surface of a static meniscus on the interval
describes a convex outer free surface of a static meniscus on the interval  , then it is stable.
, then it is stable.
Theorem 2.12.
If the solution  of the initial value problem (2.10) is concave (i.e.,
of the initial value problem (2.10) is concave (i.e.,  ) on the interval
) on the interval  , then it does not describe the outer free surface of a static meniscus on
, then it does not describe the outer free surface of a static meniscus on  .
.
Proof.

on  implies that
implies that  is strictly decreasing on
is strictly decreasing on  . Hence
. Hence  .
.
Theorem 2.13.
If  and there exists
and there exists  such that the solution of the initial value problem (2.10) is the outer free surface of a static meniscus on
such that the solution of the initial value problem (2.10) is the outer free surface of a static meniscus on  , then for
, then for  the following inequalities hold:
the following inequalities hold:

Proof.
Denote by  the solution of the initial value problem (2.10) which is assumed to represent the outer free surface of a static meniscus on the closed interval
the solution of the initial value problem (2.10) which is assumed to represent the outer free surface of a static meniscus on the closed interval  . Let
. Let  be defined as in Theorem 2.2. for
be defined as in Theorem 2.2. for  . Since
. Since  , we have
, we have  . Hence
. Hence  and therefore
and therefore  for
for  ,
,  close to
close to  . Taking into account the fact that
. Taking into account the fact that  it follows that there exists
it follows that there exists  such that
such that  .
.
Therefore  . Since
. Since  and
and  , the following inequality holds:
, the following inequality holds:  . On the other hand
. On the other hand  . Using the above evaluations we obtain inequalities (2.31).
. Using the above evaluations we obtain inequalities (2.31).
Remark 2.14.
If  appearing in Theorem 2.13 is represented as
appearing in Theorem 2.13 is represented as  ,
,  , then inequality (2.31) becomes
, then inequality (2.31) becomes

For  inequality (2.32) becomes
inequality (2.32) becomes

Theorem 2.15.
Let  be
be  . If for
. If for  the following inequality holds:
the following inequality holds:

then the solution  of the initial value problem (2.10) is concave on the interval
of the initial value problem (2.10) is concave on the interval  where
where  is the maximal interval of the existence of
is the maximal interval of the existence of  .
.
Proof.
Consider  and remark that for
and remark that for  the following relations hold:
the following relations hold:

Hence:  for
for  .
.
3. Meniscus Inner Free Surface Shape Analysis in the Case of Tube Growth
Consider now the differential equation

and  such that
such that  .
.
Definition 3.1.
A solution  of (3.1) describes the inner free surface of a static meniscus on the interval
of (3.1) describes the inner free surface of a static meniscus on the interval  if possesses the following properties:
if possesses the following properties:
-
(a)
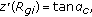
-
(b)
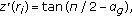 and
and -
(c)
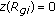 and
and 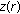 is strictly increasing on
is strictly increasing on 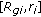 .
.
The described inner free surface is convex on  if in addition the following inequality holds:
if in addition the following inequality holds:
-
(d)
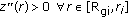 .
.
Theorem 3.2.
If there exists a solution of (3.1), which describes a convex inner free surface of a static meniscus on the closed interval , then the following inequalities hold:
, then the following inequalities hold:

Proof.
Let  be a solution of (3.1), which describes a convex inner free surface of a static meniscus on the closed interval
be a solution of (3.1), which describes a convex inner free surface of a static meniscus on the closed interval  and
and  . The function
. The function  verifies the equation
verifies the equation

and the boundary conditions

Hence, there exists  such that the following equality holds:
such that the following equality holds:

Since  ,
,  is strictly increasing and
is strictly increasing and  is strictly increasing on
is strictly increasing on  , therefore the following inequalities hold:
, therefore the following inequalities hold:

Equality (3.5) and inequalities (3.6) imply inequalities (3.2).
Corollary 3.3.
If  with
with  , then inequalities (3.2) become
, then inequalities (3.2) become

Corollary 3.4.
If  , then
, then  and (3.7) becomes
and (3.7) becomes

If  , then
, then  and
and  .
.
Theorem 3.5.
Let m be such that  . If
. If  satisfies the inequality
satisfies the inequality

then there exists  in the closed interval
in the closed interval  such that the solution of the initial value problem
such that the solution of the initial value problem

on the interval  describes the convex inner free surface of a static meniscus.
describes the convex inner free surface of a static meniscus.
Proof.
Consider the solution  of the initial value problem (3.10). Denote by
of the initial value problem (3.10). Denote by  the maximal interval on which the function
the maximal interval on which the function  exists and by
exists and by  the function
the function  defined on
defined on  . Remark that for
. Remark that for  the following equality holds:
the following equality holds:

Since

there exists  ,
,  such that for any
such that for any  the following inequalities hold:
the following inequalities hold:

Let  be defined by
be defined by

It is clear that  and for any
and for any  inequalities (3.13) hold. Moreover,
inequalities (3.13) hold. Moreover,  exists and satisfies,
exists and satisfies,  and
and  . Hence
. Hence  is finite, it is strictly positive, and for every
is finite, it is strictly positive, and for every  the following inequalities hold:
the following inequalities hold:

We will show now that  and
and  .
.
In order to show that  , we assume the contrary, that is,
, we assume the contrary, that is,  . Under this hypothesis we have
. Under this hypothesis we have

for some  . Hence
. Hence  and it follows that there exists
and it follows that there exists  such that
such that  and
and  . This last inequality is impossible according to the definition of
. This last inequality is impossible according to the definition of  .
.
Therefore,  defined by (3.14) satisfies
defined by (3.14) satisfies  .
.
In order to show that  we remark that from the definition (3.14) of
we remark that from the definition (3.14) of  it follows that at least one of the following three equalities holds:
it follows that at least one of the following three equalities holds:

Since  for
for  , it follows that the equality
, it follows that the equality  is impossible.
is impossible.
Hence we obtain that in  at least one of the following two equalities holds:
at least one of the following two equalities holds:

We show now that the equality  is impossible. For this we assume the contrary, that is,
is impossible. For this we assume the contrary, that is,  . Under this hypothesis, from (3.11), we have
. Under this hypothesis, from (3.11), we have

what is impossible.
In this way we obtain that the equality  holds.
holds.
For  the solution of the initial value problem (3.10) on the interval
the solution of the initial value problem (3.10) on the interval  describes a convex inner free surface of a static meniscus.
describes a convex inner free surface of a static meniscus.
Corollary 3.6.
If for  the following inequality holds
the following inequality holds

then there exists  in the interval
in the interval  such that the solution of the initial value problem (3.10) on the interval
such that the solution of the initial value problem (3.10) on the interval  describes a convex inner free surface of a static meniscus.
describes a convex inner free surface of a static meniscus.
Corollary 3.7.
If for  the following inequalities hold:
the following inequalities hold:

then there exists  in the interval
in the interval  such that the solution of the initial value problem (3.10) on the interval
such that the solution of the initial value problem (3.10) on the interval  describes a convex inner free surface of a static meniscus.
describes a convex inner free surface of a static meniscus.
The existence of  and the inequality
and the inequality  follows from Theorem 3.5. The inequality
follows from Theorem 3.5. The inequality  follows from the Corollary 3.3.
follows from the Corollary 3.3.
Theorem 3.8.
If a solution  of (3.1) describes a convex inner free surface of a static meniscus on the interval
of (3.1) describes a convex inner free surface of a static meniscus on the interval  , then it is a weak minimum for the energy functional of the melt column:
, then it is a weak minimum for the energy functional of the melt column:

Proof.
It is similar to the proof of Theorem 2.9.
Definition 3.9.
A solution  of (3.1) which describes the inner free surface of a static meniscus is said to be stable if it is a weak minimum of the energy functional of the melt column.
of (3.1) which describes the inner free surface of a static meniscus is said to be stable if it is a weak minimum of the energy functional of the melt column.
Remark 3.10.
Theorem 3.8 shows that if  describes a convex inner free surface of a static meniscus on the interval
describes a convex inner free surface of a static meniscus on the interval  , then it is stable.
, then it is stable.
Remark 3.11.
The solution of the initial value problem (3.10) is convex at  (i.e.,
(i.e.,  ) if and only if
) if and only if

Theorem 3.12.
If  represents the inner free surface of a static meniscus on the closed interval
represents the inner free surface of a static meniscus on the closed interval  which possesses the following properties:
which possesses the following properties:
-
(a)
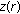 is convex at
is convex at 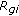 , and
, and -
(b)
the shape of
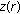 changes once on the interval
changes once on the interval 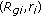 , that is, there exists a point
, that is, there exists a point 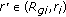 such that
such that 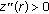 for
for 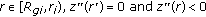 for
for 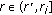 ,
,
then there exists  such that
such that  and for
and for  the following inequality holds:
the following inequality holds:

Proof.
Since  increases on
increases on  and decreases on
and decreases on  , and
, and  , there exists
, there exists  such that
such that  . The maximum value
. The maximum value  is less than
is less than  . From (3.11) we have
. From (3.11) we have

and therefore

Remark 3.13.
If the solution  of the initial value problem (3.10) is concave (i.e.,
of the initial value problem (3.10) is concave (i.e.,  ) on the interval
) on the interval , then it does not describe the inner free surface of a static meniscus on
, then it does not describe the inner free surface of a static meniscus on  .
.
Theorem 3.14.
Let  be
be  . If for
. If for  the following inequality holds:
the following inequality holds:

then the solution  of the initial value problem (3.10) is concave on the interval
of the initial value problem (3.10) is concave on the interval  where
where  is the maximal interval of the existence of
is the maximal interval of the existence of  .
.
Proof.
Consider  and remark that for
and remark that for  the following relations hold:
the following relations hold:

Hence  for
for  .
.
4. Numerical Illustration
Numerical computations were performed for a Si cylindrical tube for the following data:

The objective was to verify if the necessary conditions are also sufficient, or if the sufficient conditions are also necessary. Moreover, the above data were used in experiments and the computed results can be tested against the experiments in order to evaluate the accuracy of the theoretical predictions. This test is not the subject of this paper.
For the considered numerical data, inequality (2.7) becomes

Integration of (2.10) shows that for  there exists
there exists  such that the solution is a convex outer free surface of a static meniscus on
such that the solution is a convex outer free surface of a static meniscus on  , but for
, but for  there is no
there is no  such that the solution is a convex outer free surface of a static meniscus on
such that the solution is a convex outer free surface of a static meniscus on  (Figures 2 and 3). Hence, inequality (2.7) is not a sufficient condition.
(Figures 2 and 3). Hence, inequality (2.7) is not a sufficient condition.
For the same numerical data inequality (2.9) becomes  . We have already obtained that for
. We have already obtained that for  there exists
there exists  in the interval
in the interval  such that the solution of (2.10) describes a convex outer free surface of a static meniscus on the interval
such that the solution of (2.10) describes a convex outer free surface of a static meniscus on the interval  . Hence, inequality (2.9) is not a necessary condition.
. Hence, inequality (2.9) is not a necessary condition.
For the same numerical data inequality (2.19) becomes  . Integration shows that for
. Integration shows that for  there exists
there exists  , such that the solution of (2.10) describes a convex outer free surface of a static meniscus on the closed interval
, such that the solution of (2.10) describes a convex outer free surface of a static meniscus on the closed interval  (Figures 4 and 5). Hence, inequality (2.19) is not a necessary condition.
(Figures 4 and 5). Hence, inequality (2.19) is not a necessary condition.
For the same numerical data inequality (2.20) becomes  . Integration of (2.10) illustrates the above phenomenon for
. Integration of (2.10) illustrates the above phenomenon for  (Figures 6 and 7) and also the fact that the condition is not necessary (see
(Figures 6 and 7) and also the fact that the condition is not necessary (see  ).
).
For the same numerical data inequality (2.21) becomes  . Integration of (2.10) illustrates the above phenomenon for
. Integration of (2.10) illustrates the above phenomenon for  (Figures 8 and 9).
(Figures 8 and 9).
For the considered numerical data inequality (2.32) becomes  . Integration shows that for
. Integration shows that for  there is no
there is no  such that the solution of (2.10) is a nonglobally convex outer free surface of a static meniscus on
such that the solution of (2.10) is a nonglobally convex outer free surface of a static meniscus on  . Moreover, for
. Moreover, for  it is not anymore the outer free surface of a static meniscus (Figures 10 and 11). Hence, inequality (2.32) is not a sufficient condition.
it is not anymore the outer free surface of a static meniscus (Figures 10 and 11). Hence, inequality (2.32) is not a sufficient condition.
For the same numerical data inequality (2.33) becomes  . We have already obtained that for
. We have already obtained that for  (Figure 10) the solution of (2.10) is not anymore the outer free surface of a static meniscus. Hence, inequality (2.33) is not a sufficient condition.
(Figure 10) the solution of (2.10) is not anymore the outer free surface of a static meniscus. Hence, inequality (2.33) is not a sufficient condition.
For the same numerical data inequality (2.34) becomes  . Integration of (2.10) for
. Integration of (2.10) for  proves that the solution is globally concave on
proves that the solution is globally concave on  (Figures 12 and 13). Hence, inequality (2.34) is not a necessary condition.
(Figures 12 and 13). Hence, inequality (2.34) is not a necessary condition.
For the considered numerical data inequality (3.7) becomes  . Integration of (3.10) shows that for
. Integration of (3.10) shows that for  there exists
there exists  such that the solution is a convex inner free surface of a static meniscus on
such that the solution is a convex inner free surface of a static meniscus on  , but for
, but for  there is no
there is no  such that the solution is a convex inner free surface of a static meniscus on
such that the solution is a convex inner free surface of a static meniscus on  (Figures 14 and 15). Hence, inequality (3.7) is not a sufficient condition.
(Figures 14 and 15). Hence, inequality (3.7) is not a sufficient condition.
For the considered numerical data (3.9) becomes  . We have already obtained that for
. We have already obtained that for  there exists
there exists  such that the solution of (3.10) describes a convex inner free surface of a static meniscus on
such that the solution of (3.10) describes a convex inner free surface of a static meniscus on  . Hence, inequality (3.9) is not a necessary condition.
. Hence, inequality (3.9) is not a necessary condition.
For the considered numerical data (3.20) becomes  Integration of (3.10) shows that for
Integration of (3.10) shows that for  there exists
there exists  such that the solution describes a convex inner free surface of a static meniscus on
such that the solution describes a convex inner free surface of a static meniscus on  (Figures 16 and 17). Hence, inequality (3.20) is not a necessary condition.
(Figures 16 and 17). Hence, inequality (3.20) is not a necessary condition.
For the considered numerical data (3.21) becomes  . Integration of (3.10) illustrates the above phenomenon for
. Integration of (3.10) illustrates the above phenomenon for  and also the fact that the condition is not necessary (Figures 18 and 19) (see
and also the fact that the condition is not necessary (Figures 18 and 19) (see  .
.
For the same numerical data inequality (3.23) becomes  . Integration of (3.10) illustrates the above phenomenon for
. Integration of (3.10) illustrates the above phenomenon for  (Figures 20 and 21).
(Figures 20 and 21).
For the considered numerical data inequality (3.24) becomes  . Integration shows that for
. Integration shows that for  there exists
there exists  such that the solution of (3.10) is a nonglobally convex inner free surface of a static meniscus on
such that the solution of (3.10) is a nonglobally convex inner free surface of a static meniscus on  , but for
, but for  it is not anymore the inner free surface of a nonglobally static meniscus (Figures 20 and 21). Hence, (3.24) is not a sufficient condition.
it is not anymore the inner free surface of a nonglobally static meniscus (Figures 20 and 21). Hence, (3.24) is not a sufficient condition.
For the same numerical data (3.27) becomes  . Integration of (3.8) for
. Integration of (3.8) for  proves that the solution is globally concave on
proves that the solution is globally concave on  (Figures 22 and 23). Hence, (3.27) is not a necessary condition.
(Figures 22 and 23). Hence, (3.27) is not a necessary condition.
5. Conclusions
(1) Inequalities (2.2) and (2.7) localize regions on the pressure axis where the outer pressure has to be taken in order to obtain convex outer free surface.
Inequalities (2.9), (2.19), and (2.20) localize regions on the pressure axis, having the property that if the outer pressure is taken in this region, then a convex outer free surface is obtained.
Inequalities (2.31) and (2.32) localize region on the pressure axis, where the outer pressure has to be taken in order to obtain a convex-concave outer free surface.
(2) Inequalities (3.2) and (3.7) localize regions on the pressure axis where the inner pressure has to be taken in order to obtain convex inner free surface.
Inequalities (3.5), (3.20), and (3.21) localize regions on the pressure axis, having the property that if the inner pressure is taken in this region, then a convex inner free surface is obtained.
Inequality (3.24) localizes region on the pressure axis, where the inner pressure has to be taken in order to obtain a convex-concave inner free surface.
(3) By computation these values are found in a real case, and the "accuracy" (sufficiency or necessity) of the reported inequalities is discussed.
References
Erris L, Stormont RW, Surek T, Taylor AS: The growth of silicon tubes by the EFG process. Journal of Crystal Growth 1980,50(1):200–211. 10.1016/0022-0248(80)90244-4
Kalejs JP, Menna AA, Stormont RW, Hutchinson JW: Stress in thin hollow silicon cylinders grown by the edge-defined film-fed growth technique. Journal of Crystal Growth 1990,104(1):14–19. 10.1016/0022-0248(90)90301-Z
Finn R: Equilibrium Capillary Surfaces, Grundlehren der Mathematischen Wissenschaften. Volume 284. Springer, New York, NY, USA; 1986:xvi+245.
Tatarchenko VA: Shaped Crystal Growth. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1993.
Rossolenko SN: Menisci masses and weights in Stepanov (EFG) technique: ribbon, rod, tube. Journal of Crystal Growth 2001,231(1–2):306–315. 10.1016/S0022-0248(01)01448-8
Yang B, Zheng LL, Mackintosh B, Yates D, Kalejs J: Meniscus dynamics and melt solidification in the EFG silicon tube growth process. Journal of Crystal Growth 2006,293(2):509–516. 10.1016/j.jcrysgro.2006.05.068
Hartman P: Ordinary Differential Equations. John Wiley & Sons, New York, NY, USA; 1964:xiv+612.
Acknowledgments
The authors thank the anonymous referees for their valuable comments and suggestions, which led to an improvement of the manuscript. They are grateful to the Romanian National Authority for Research supporting this research under the Grant ID 354 no. 7/2007.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Balint, S., Balint, A.M. Inequalities for Single Crystal Tube Growth by Edge-Defined Film-Fed Growth Technique. J Inequal Appl 2009, 732106 (2009). https://doi.org/10.1155/2009/732106
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/732106

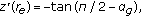
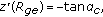 and
and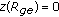 and
and 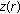 is strictly decreasing on
is strictly decreasing on 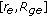 .
.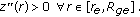
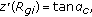
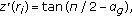 and
and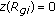 and
and 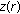 is strictly increasing on
is strictly increasing on 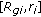 .
.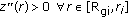 .
.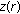 is convex at
is convex at 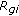 , and
, and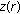 changes once on the interval
changes once on the interval 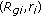 , that is, there exists a point
, that is, there exists a point 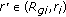 such that
such that 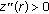 for
for 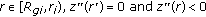 for
for 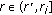 ,
,
 versus
versus  for
for  .
.
 versus
versus  .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.