- Research Article
- Open access
- Published:
Strong and  Convergence Theorems for Multivalued Mappings in
Convergence Theorems for Multivalued Mappings in  Spaces
Spaces
Journal of Inequalities and Applications volume 2009, Article number: 730132 (2009)
Abstract
We show strong and  convergence for Mann iteration of a multivalued nonexpansive mapping whose domain is a nonempty closed convex subset of a CAT(0) space. The results we obtain are analogs of Banach space results by Song and Wang [2009, 2008]. Strong convergence of Ishikawa iteration are also included.
convergence for Mann iteration of a multivalued nonexpansive mapping whose domain is a nonempty closed convex subset of a CAT(0) space. The results we obtain are analogs of Banach space results by Song and Wang [2009, 2008]. Strong convergence of Ishikawa iteration are also included.
1. Introduction
Let  be a nonempty subset of a Banach space
be a nonempty subset of a Banach space  We shall denote by
We shall denote by  the family of nonempty closed bounded subsets of
the family of nonempty closed bounded subsets of  by
by  the family of nonempty bounded proximinal subsets of
the family of nonempty bounded proximinal subsets of  and by
and by  the family of nonempty compact subsets of
the family of nonempty compact subsets of  . Let
. Let  be the Hausdorff distance on
be the Hausdorff distance on  that is,
that is,

where  is the distance from the point
is the distance from the point  to the set
to the set 
A multivalued mapping  is said to be a nonexpansive if
is said to be a nonexpansive if

A point  is called a fixed point of
is called a fixed point of  if
if  We denote by
We denote by  the set of all fixed points of
the set of all fixed points of 
In 2005, Sastry and Babu [1] introduced the Mann and Ishikawa iterations for multivalued mappings as follows: let  be a real Hilbert space and
be a real Hilbert space and  be a multivalued mapping for which
be a multivalued mapping for which  . Fix
. Fix  and define
and define
-
(A)
the sequence of Mann iterates by

 (1.3)
(1.3)where
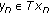 is such that
is such that 
-
(B)
the sequence of Ishikawa iterates by

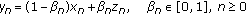 (1.4)
(1.4)
where  is such that
is such that  and
and

where  is such that
is such that 
They proved the following results.
Theorem 1.1.
Let  be a nonempty compact convex subset of a Hilbert space
be a nonempty compact convex subset of a Hilbert space  Suppose
Suppose  is nonexpansive and has a fixed point
is nonexpansive and has a fixed point  Assume that (i)
Assume that (i)  and (ii)
and (ii) Then the sequence of Mann iterates defined by (A) converges to a fixed point
Then the sequence of Mann iterates defined by (A) converges to a fixed point  of
of 
Theorem 1.2.
Let  be a nonempty compact convex subset of a Hilbert space
be a nonempty compact convex subset of a Hilbert space  Suppose that a nonexpansive map
Suppose that a nonexpansive map  has a fixed point
has a fixed point  Assume that (i)
Assume that (i) (ii)
(ii)  and (iii)
and (iii) Then the sequence of Ishikawa iterates defined by (B) converges to a fixed point
Then the sequence of Ishikawa iterates defined by (B) converges to a fixed point  of
of 
In 2007, Panyanak [2] extended Sastry-Babu's results to uniformly convex Banach spaces as the following results.
Theorem 1.3.
Let  be a nonempty compact convex subset of a uniformly convex Banach spaces
be a nonempty compact convex subset of a uniformly convex Banach spaces  Suppose that a nonexpansive map
Suppose that a nonexpansive map  has a fixed point
has a fixed point  Let
Let  be the sequence of Mann iterates defined by (A). Assume that (i)
be the sequence of Mann iterates defined by (A). Assume that (i) and (ii)
and (ii) Then the sequence
Then the sequence  converges to a fixed point of
converges to a fixed point of 
Theorem 1.4.
Let  be a nonempty compact convex subset of a uniformly convex Banach spaces
be a nonempty compact convex subset of a uniformly convex Banach spaces  Suppose that a nonexpansive map
Suppose that a nonexpansive map  has a fixed point
has a fixed point  . Let
. Let  be the sequence of Ishikawa iterates defined by (B). Assume that (i)
be the sequence of Ishikawa iterates defined by (B). Assume that (i) (ii)
(ii) and (iii)
and (iii) Then the sequence
Then the sequence  converges to a fixed point of
converges to a fixed point of 
Recently, Song and Wang [3, 4] pointed out that the proof of Theorem 1.4 contains a gap. Namely, the iterative sequence  defined by (B) depends on the fixed point
defined by (B) depends on the fixed point  Clearly, if
Clearly, if  and
and  then the sequence
then the sequence  defined by
defined by  is different from the one defined by
is different from the one defined by  Thus, for
Thus, for  defined by
defined by  , we cannot obtain that
, we cannot obtain that  is a decreasing sequence from the monotony of
is a decreasing sequence from the monotony of  . Hence, the conclusion of Theorem 1.4 (also Theorem 1.3) is very dubious.
. Hence, the conclusion of Theorem 1.4 (also Theorem 1.3) is very dubious.
Motivated by solving the above gap, they defined the modified Mann and Ishikawa iterations as follows.
Let  be a nonempty convex subset of a Banach space
be a nonempty convex subset of a Banach space  and
and  be a multivalued mapping. The sequence of Mann iterates is defined as follows: let
be a multivalued mapping. The sequence of Mann iterates is defined as follows: let  and
and  such that
such that  Choose
Choose  and
and  Let
Let

There exists  such that
such that  (see [5, 6]). Take
(see [5, 6]). Take

Inductively, we have

where  such that
such that 
The sequence of Ishikawa iterates is defined as follows: let  ,
,  and
and  such that
such that  Choose
Choose  and
and  Let
Let

There exists  such that
such that  Let
Let

There is  such that
such that  Take
Take

There exists  such that
such that  Let
Let

Inductively, we have

where  and
and  such that
such that  and
and 
They obtained the following results.
Theorem 1.5 (see [3, Theorem 2.3]).
Let  be a nonempty compact convex subset of a Banach space
be a nonempty compact convex subset of a Banach space  Suppose that
Suppose that  is a multivalued nonexpansive mapping for which
is a multivalued nonexpansive mapping for which  and
and  for each
for each  Let
Let  be the sequence of Mann iteration defined by (1.8). Assume that
be the sequence of Mann iteration defined by (1.8). Assume that

Then the sequence  strongly converges to a fixed point of
strongly converges to a fixed point of 
Recall that a multivalued mapping  is said to satisfy Condition I ([7]) if there exists a nondecreasing function
is said to satisfy Condition I ([7]) if there exists a nondecreasing function  with
with  and
and  for all
for all  such that
such that

Theorem 1.6 (see [3, Theorem 2.4]).
Let  be a nonempty closed convex subset of a Banach space
be a nonempty closed convex subset of a Banach space  Suppose that
Suppose that  is a multivalued nonexpansive mapping that satisfies Condition I. Let
is a multivalued nonexpansive mapping that satisfies Condition I. Let  be the sequence of Mann iteration defined by (1.8). Assume that
be the sequence of Mann iteration defined by (1.8). Assume that  and satisfies
and satisfies  for each
for each  and
and

Then the sequence  strongly converges to a fixed point of
strongly converges to a fixed point of 
Theorem 1.7 (see [3, Theorem 2.5]).
Let  be a Banach space satisfying Opial's condition and
be a Banach space satisfying Opial's condition and  be a nonempty weakly compact convex subset of
be a nonempty weakly compact convex subset of  Suppose that
Suppose that  is a multivalued nonexpansive mapping. Let
is a multivalued nonexpansive mapping. Let  be the sequence of Mann iteration defined by (1.8). Assume that
be the sequence of Mann iteration defined by (1.8). Assume that  and satisfies
and satisfies  for each
for each  and
and

Then the sequence  weakly converges to a fixed point of
weakly converges to a fixed point of 
Theorem 1.8 (see [4, Theorem 1]).
Let  be a nonempty compact convex subset of a uniformly convex Banach space
be a nonempty compact convex subset of a uniformly convex Banach space  Suppose that
Suppose that  is a multivalued nonexpansive mapping and
is a multivalued nonexpansive mapping and  satisfying
satisfying  for any fixed point
for any fixed point  Let
Let  be the sequence of Ishikawa iterates defined by (1.13). Assume that (i)
be the sequence of Ishikawa iterates defined by (1.13). Assume that (i) (ii)
(ii) and (iii)
and (iii) Then the sequence
Then the sequence  strongly converges to a fixed point of
strongly converges to a fixed point of 
Theorem 1.9 (see [4, Theorem 2]).
Let  be a nonempty closed convex subset of a uniformly convex Banach space
be a nonempty closed convex subset of a uniformly convex Banach space  Suppose that
Suppose that  is a multivalued nonexpansive mapping that satisfy Condition I. Let
is a multivalued nonexpansive mapping that satisfy Condition I. Let  be the sequence of Ishikawa iterates defined by (1.13). Assume that
be the sequence of Ishikawa iterates defined by (1.13). Assume that  satisfying
satisfying  for any fixed point
for any fixed point  and
and  Then the sequence
Then the sequence  strongly converges to a fixed point of
strongly converges to a fixed point of 
In this paper, we study the iteration processes defined by (1.8) and (1.13) in a CAT(0) space and give analogs of Theorems 1.5–1.9 in this setting.
2.  Spaces
Spaces
A metric space  is a CAT(0) space if it is geodesically connected, and if every geodesic triangle in
is a CAT(0) space if it is geodesically connected, and if every geodesic triangle in  is at least as "thin" as its comparison triangle in the Euclidean plane. The precise definition is given below. It is well known that any complete, simply connected Riemannian manifold having nonpositive sectional curvature is a CAT
is at least as "thin" as its comparison triangle in the Euclidean plane. The precise definition is given below. It is well known that any complete, simply connected Riemannian manifold having nonpositive sectional curvature is a CAT space. Other examples include Pre-Hilbert spaces,
space. Other examples include Pre-Hilbert spaces,  -trees (see [8]), Euclidean buildings (see [9]), the complex Hilbert ball with a hyperbolic metric (see [10]), and many others. For a thorough discussion of these spaces and of the fundamental role they play in geometry (see Bridson and Haefliger [8]). Burago, et al. [11] contains a somewhat more elementary treatment, and Gromov [12] a deeper study.
-trees (see [8]), Euclidean buildings (see [9]), the complex Hilbert ball with a hyperbolic metric (see [10]), and many others. For a thorough discussion of these spaces and of the fundamental role they play in geometry (see Bridson and Haefliger [8]). Burago, et al. [11] contains a somewhat more elementary treatment, and Gromov [12] a deeper study.
Fixed point theory in a CAT(0) space was first studied by Kirk (see [13] and [14]). He showed that every nonexpansive (single-valued) mapping defined on a bounded closed convex subset of a complete CAT(0) space always has a fixed point. Since then the fixed point theory for single-valued and multivalued mappings in CAT(0) spaces has been rapidly developed and many of papers have appeared (see, e.g., [15–24]). It is worth mentioning that the results in CAT(0) spaces can be applied to any CAT( ) space with
) space with  since any CAT(
since any CAT( ) space is a CAT(
) space is a CAT(  ) space for every
) space for every  (see [8], page 165).
(see [8], page 165).
Let  be a metric space. A geodesic path joining
be a metric space. A geodesic path joining  to
to  (or, more briefly, a geodesic from
(or, more briefly, a geodesic from  to
to  ) is a map
) is a map  from a closed interval
from a closed interval  to
to  such that
such that  and
and  for all
for all  In particular,
In particular,  is an isometry and
is an isometry and  The image
The image  of
of  is called a geodesic (or metric) segment joining
is called a geodesic (or metric) segment joining  and
and  . When it is unique this geodesic is denoted by
. When it is unique this geodesic is denoted by  . The space
. The space  is said to be a geodesic space if every two points of
is said to be a geodesic space if every two points of  are joined by a geodesic, and
are joined by a geodesic, and  is said to be uniquely geodesic if there is exactly one geodesic joining
is said to be uniquely geodesic if there is exactly one geodesic joining  and
and  for each
for each  A subset
A subset  is said to be convex if
is said to be convex if  includes every geodesic segment joining any two of its points.
includes every geodesic segment joining any two of its points.
A geodesic triangle in a geodesic space
in a geodesic space  consists of three points
consists of three points  in
in  (the vertices of
(the vertices of  ) and a geodesic segment between each pair of vertices (the edges of
) and a geodesic segment between each pair of vertices (the edges of  ). A comparison triangle for geodesic triangle
). A comparison triangle for geodesic triangle  in
in  is a triangle
is a triangle  in the Euclidean plane
in the Euclidean plane  such that
such that  for
for 
A geodesic space is said to be a CAT(0) space if all geodesic triangles satisfy the following comparison axiom.
CAT(0): let  be a geodesic triangle in
be a geodesic triangle in  and let
and let  be a comparison triangle for
be a comparison triangle for  . Then
. Then  is said to satisfy the CAT(0) inequality if for all
is said to satisfy the CAT(0) inequality if for all  and all comparison points
and all comparison points 

Let  by [24, Lemma 2.1(iv)] for each
by [24, Lemma 2.1(iv)] for each  there exists a unique point
there exists a unique point  such that
such that

From now on we will use the notation  for the unique point
for the unique point  satisfying (2.2). By using this notation Dhompongsa and Panyanak [24] obtained the following lemma which will be used frequently in the proof of our main theorems.
satisfying (2.2). By using this notation Dhompongsa and Panyanak [24] obtained the following lemma which will be used frequently in the proof of our main theorems.
Lemma 2.1.
Let  be a CAT (0)space . Then
be a CAT (0)space . Then

for all  and
and 
If  are points in a CAT(0) space and if
are points in a CAT(0) space and if  then the CAT(0) inequality implies
then the CAT(0) inequality implies

This is the (CN) inequality of Bruhat and Tits [25]. In fact (cf. [8, page 163]), a geodesic metric space is a CAT(0) space if and only if it satisfies (CN).
The following lemma is a generalization of the (CN) inequality which can be found in [24].
Lemma 2.2.
Let  be a CAT(0) space. Then
be a CAT(0) space. Then

for all  and
and 
The preceding facts yield the following result.
Proposition 2.3.
Let  be a geodesic space. Then the following are equivalent:
be a geodesic space. Then the following are equivalent:
-
(i)
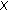 is a CAT (0) space;
is a CAT (0) space; -
(ii)
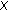 satisfies (CN);
satisfies (CN); -
(iii)
 satisfies (2.5).
satisfies (2.5).
The existence of fixed points for multivalued nonexpansive mappings in a CAT(0) space was proved by S. Dhompongsa et al. [17], as follows.
Theorem 2.4.
Let  be a closed convex subset of a complete CAT(0) space
be a closed convex subset of a complete CAT(0) space  , and let
, and let  be a nonexpansive nonself-mapping. Suppose
be a nonexpansive nonself-mapping. Suppose

for some bounded sequence  in
in  Then
Then  has a fixed point.
has a fixed point.
3. The Setting
Let  be a Banach space, and let
be a Banach space, and let  be a bounded sequence in
be a bounded sequence in  for
for  we let
we let

The asymptotic radius of
of  is given by
is given by

and the asymptotic center of
of  is the set
is the set

The notion of asymptotic centers in a Banach space  can be extended to a CAT(0) space
can be extended to a CAT(0) space  as well, simply replacing
as well, simply replacing  with
with  It is known (see, e.g., [18, Proposition 7]) that in a CAT(0) space,
It is known (see, e.g., [18, Proposition 7]) that in a CAT(0) space,  consists of exactly one point.
consists of exactly one point.
Next we provide the definition and collect some basic properties of  -convergence.
-convergence.
Definition 3.1 (see [23]).
A sequence  in a CAT(0) space
in a CAT(0) space  is said to
is said to  -converge to
-converge to  if
if  is the unique asymptotic center of
is the unique asymptotic center of  for every subsequence
for every subsequence  of
of  . In this case one must write
. In this case one must write  and call
and call  the
the  -limit of
-limit of 
Remark 3.2.
In a CAT(0) space  , strong convergence implies
, strong convergence implies  convergence and they are coincided when
convergence and they are coincided when  is a Hilbert space. Indeed, we prove a much more general result. Recall that a Banach space is said to satisfy Opial's condition ([26]) if given whenever
is a Hilbert space. Indeed, we prove a much more general result. Recall that a Banach space is said to satisfy Opial's condition ([26]) if given whenever  converges weakly to
converges weakly to 

Proposition 3.3.
Let  be a reflexive Banach space satisfying Opial's condition and let
be a reflexive Banach space satisfying Opial's condition and let  be a bounded sequence in
be a bounded sequence in  and let
and let  Then
Then  converges weakly to
converges weakly to  if and only if
if and only if  for all subsequence
for all subsequence  of
of 
Proof.
( ) Let
) Let  be a subsequence of
be a subsequence of  . Then
. Then  converges weakly to
converges weakly to  By Opial's condition
By Opial's condition  (
( ) Suppose
) Suppose  for all subsequence
for all subsequence  of
of  and assume that
and assume that  does not converge weakly to
does not converge weakly to  Then there exists a subsequence
Then there exists a subsequence  of
of  such that for each
such that for each  is outside a weak neighborhood of
is outside a weak neighborhood of  Since
Since  is bounded, without loss of generality we may assume that
is bounded, without loss of generality we may assume that  converges weakly to
converges weakly to  By Opial's condition
By Opial's condition  a contradiction.
a contradiction.
Lemma 3.4.
(i) Every bounded sequence in  has a
has a  convergent subsequence (see [23, page 3690]). (ii) If
convergent subsequence (see [23, page 3690]). (ii) If  is a closed convex subset of
is a closed convex subset of  and if
and if  is a bounded sequence in
is a bounded sequence in  then the asymptotic center of
then the asymptotic center of  is in
is in  (see [17, Proposition 2.1]).
(see [17, Proposition 2.1]).
Now, we define the sequences of Mann and Ishikawa iterates in a CAT(0) space which are analogs of the two defined in Banach spaces by Song and Wang [3, 4].
Definition 3.5.
Let  be a nonempty convex subset of a CAT(0) space
be a nonempty convex subset of a CAT(0) space  and
and  be a multivalued mapping. The sequence of Mann iterates is defined as follows: let
be a multivalued mapping. The sequence of Mann iterates is defined as follows: let  and
and  such that
such that  Choose
Choose  and
and  Let
Let

There exists  such that
such that  Take
Take

Inductively, we have

where  such that
such that 
Definition 3.6.
Let  be a nonempty convex subset of a CAT(0) space
be a nonempty convex subset of a CAT(0) space  and
and  be a multivalued mapping. The sequence of Ishikawa iterates is defined as follows: let
be a multivalued mapping. The sequence of Ishikawa iterates is defined as follows: let  ,
,  and
and  such that
such that  Choose
Choose  and
and  Let
Let

There exists  such that
such that  Let
Let

There is  such that
such that  Take
Take

There exists  such that
such that  Let
Let

Inductively, we have

where  and
and  such that
such that  and
and 
Lemma 3.7.
Let  be a nonempty compact convex subset of a complete CAT (0) space
be a nonempty compact convex subset of a complete CAT (0) space  and let
and let  be a nonexpansive nonself-mapping. Suppose that
be a nonexpansive nonself-mapping. Suppose that

for some sequence  in
in  Then
Then  has a fixed point. Moreover, if
has a fixed point. Moreover, if  converges for each
converges for each  , then
, then  strongly converges to a fixed point of
strongly converges to a fixed point of 
Proof.
By the compactness of  there exists a subsequence
there exists a subsequence  of
of  such that
such that  Thus
Thus

This implies that  is a fixed point of
is a fixed point of  Since the limit of
Since the limit of  exists and
exists and  we have
we have  This show that the sequence
This show that the sequence  strongly converges to
strongly converges to 
Before proving our main results we state a lemma which is an analog of Lemma 2.2 of [27]. The proof is metric in nature and carries over to the present setting without change.
Lemma 3.8.
Let  and
and  be bounded sequences in a CAT (0)space
be bounded sequences in a CAT (0)space  and let
and let  be a sequence in
be a sequence in  with
with  Suppose that
Suppose that  for all
for all  and
and

Then 
4. Strong and  Convergence of Mann Iteration
Convergence of Mann Iteration
Theorem 4.1.
Let  be a nonempty compact convex subset of a complete CAT (0)space
be a nonempty compact convex subset of a complete CAT (0)space  Suppose that
Suppose that  is a multivalued nonexpansive mapping and
is a multivalued nonexpansive mapping and  satisfying
satisfying  for any fixed point
for any fixed point  If
If  is the sequence of Mann iterates defined by (3.7) such that one of the following two conditions is satisfied:
is the sequence of Mann iterates defined by (3.7) such that one of the following two conditions is satisfied:
-
(i)
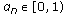 and
and 
-
(ii)
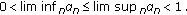
Then the sequence  strongly converges to a fixed point of
strongly converges to a fixed point of 
Proof
Case 1.
Suppose that (i) is satisfied. Let  by Lemma 2.2 and the nonexpansiveness of
by Lemma 2.2 and the nonexpansiveness of  we have
we have

This implies


It follows from (4.2) that  for all
for all  This implies that
This implies that  is bounded and decreasing. Hence
is bounded and decreasing. Hence  exists for all
exists for all  On the other hand, (4.3) implies
On the other hand, (4.3) implies

Since  diverges, we have
diverges, we have  and hence
and hence  Then there exists a subsequence
Then there exists a subsequence  of
of  such that
such that

This implies

By Lemma 3.7,  converges to a point
converges to a point  Since the limit of
Since the limit of  exists, it must be the case that
exists, it must be the case that  and hence the conclusion follows.
and hence the conclusion follows.
Case 2.
If (ii) is satisfied. As in the Case 1,  exists for each
exists for each  It follows from the definition of Mann iteration (3.7) that
It follows from the definition of Mann iteration (3.7) that

Therefore,

By Lemma 3.8, we obtain

This implies

so the conclusion follows from Lemma 3.7.
Theorem 4.2.
Let  be a nonempty closed convex subset of a complete CAT(0) space
be a nonempty closed convex subset of a complete CAT(0) space  Suppose that
Suppose that  is a multivalued nonexpansive mapping that satisfies Condition I. Let
is a multivalued nonexpansive mapping that satisfies Condition I. Let  be the sequence of Mann iterates defined by (3.7). Assume that
be the sequence of Mann iterates defined by (3.7). Assume that  satisfying
satisfying  for any fixed point
for any fixed point  and
and  Then the sequence
Then the sequence  strongly converges to a fixed point of
strongly converges to a fixed point of 
Proof.
It follows from the proof of the Case 1 in Theorem 4.1 that  exists for each
exists for each  and
and

Then

This implies

Thus,  and hence
and hence  Since
Since 

Therefore,  Furthermore Condition I implies
Furthermore Condition I implies

The proof of remaining part closely follows the proof of of [2, Theorem 3.8], simply replacing  with
with  .
.
Next we show a  convergence theorem of Mann iteration in a CAT(0) space setting which is an analog of Theorem 1.7. For this we need more lemmas.
convergence theorem of Mann iteration in a CAT(0) space setting which is an analog of Theorem 1.7. For this we need more lemmas.
Lemma 4.3 (see [24, Lemma 2.8]).
If  is a bounded sequence in a complete CAT (0)space
is a bounded sequence in a complete CAT (0)space  with
with  and
and  is a subsequence of
is a subsequence of  with
with  and the sequence
and the sequence  converges, then
converges, then 
Lemma 4.4.
Let  be a nonempty closed convex subset of a complete CAT (0) space
be a nonempty closed convex subset of a complete CAT (0) space  and let
and let  be a nonexpansive nonself-mapping. Suppose that
be a nonexpansive nonself-mapping. Suppose that  is a sequence in
is a sequence in  which
which  converges to
converges to  in
in  and
and

Then 
Proof.
Notice from Lemma 3.4(ii) that  Since
Since  is compact-valued, for each
is compact-valued, for each  there exists
there exists  and
and  such that
such that  and
and  It follows from (4.16) that
It follows from (4.16) that

By the compactness of  there exists a subsequence
there exists a subsequence  of
of  such that
such that  Then
Then

This implies

Since  and hence
and hence  by (4.19). Therefore
by (4.19). Therefore  is a fixed point of
is a fixed point of 
Lemma 4.5.
Let  be a closed convex subset of a complete CAT (0)space
be a closed convex subset of a complete CAT (0)space and let
and let  be a nonexpansive mapping. Suppose
be a nonexpansive mapping. Suppose is a bounded sequence in
is a bounded sequence in  such that
such that and
and converges for all
converges for all then
then  Here
Here  where the union is taken over all subsequences
where the union is taken over all subsequences  of
of  Moreover,
Moreover,  consists of exactly one point.
consists of exactly one point.
Proof.
Let  , then there exists a subsequence
, then there exists a subsequence  of
of  such that
such that  By Lemma 3.4(i) and (ii) there exists a subsequence
By Lemma 3.4(i) and (ii) there exists a subsequence  of
of  such that
such that  . By Lemma 4.4,
. By Lemma 4.4,  . By Lemma 4.3,
. By Lemma 4.3,  This shows that
This shows that  Next, we show that
Next, we show that  consists of exactly one point. Let
consists of exactly one point. Let  be a subsequence of
be a subsequence of  with
with  and let
and let  . Since
. Since  is convergent by the assumption. By Lemma 4.3,
is convergent by the assumption. By Lemma 4.3,  This completes the proof.
This completes the proof.
Theorem 4.6.
Let  be a nonempty closed convex subset of a complete CAT (0) space
be a nonempty closed convex subset of a complete CAT (0) space  Suppose that
Suppose that  is a multivalued nonexpansive mapping. Let
is a multivalued nonexpansive mapping. Let  be the sequence of Mann iterates defined by (3.7). Assume that
be the sequence of Mann iterates defined by (3.7). Assume that  satisfying
satisfying  for any fixed point
for any fixed point  and
and

Then the sequence  converges to a fixed point of
converges to a fixed point of 
Proof.
Let  it follows from (4.2) in the proof of Theorem 4.1 that
it follows from (4.2) in the proof of Theorem 4.1 that  for all
for all  This implies that
This implies that  is bounded and decreasing. Hence
is bounded and decreasing. Hence  exists for all
exists for all  Since
Since 

Thus  by (4.9). By Lemma 4.5,
by (4.9). By Lemma 4.5,  consists of exactly one point and is contained in
consists of exactly one point and is contained in  . This shows that
. This shows that  converges to an element of
converges to an element of 
5. Strong Convergence of Ishikawa Iteration
The following lemma can be found in [2].
Lemma 5.1.
Let  be two real sequences such that
be two real sequences such that
-
(i)
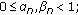
-
(ii)
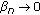 as
as 
-
(iii)
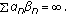
Let  be a nonnegative real sequence such that
be a nonnegative real sequence such that  is bounded. Then
is bounded. Then  has a subsequence which converges to zero.
has a subsequence which converges to zero.
The following theorem is an analog of Theorem 1.8.
Theorem 5.2.
Let  be a nonempty compact convex subset of a complete CAT (0) space
be a nonempty compact convex subset of a complete CAT (0) space  Suppose that
Suppose that  is a multivalued nonexpansive mapping and
is a multivalued nonexpansive mapping and  satisfying
satisfying  for any fixed point
for any fixed point  Let
Let  be the sequence of Ishikawa iterates defined by (3.12). Assume that
be the sequence of Ishikawa iterates defined by (3.12). Assume that
-
(i)

-
(ii)
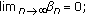
-
(iii)

Then the sequence  strongly converges to a fixed point of
strongly converges to a fixed point of 
Proof.
Let  by Lemma 2.2 and the nonexpansiveness of
by Lemma 2.2 and the nonexpansiveness of  we have
we have

This implies


It follows from (5.2) that the sequence  is decreasing and hence
is decreasing and hence  exists for each
exists for each  On the other hand, (5.3) implies
On the other hand, (5.3) implies

By Lemma 5.1, there exists a subsequence  of
of  such that
such that

This implies

By Lemma 3.7,  converges to a point
converges to a point  Since the limit of
Since the limit of  exists, it must be the case that
exists, it must be the case that  and hence the conclusion follows.
and hence the conclusion follows.
The following theorem is an analog of Theorem 1.9.
Theorem 5.3.
Let  be a nonempty closed convex subset of a complete CAT(0) space
be a nonempty closed convex subset of a complete CAT(0) space  Suppose that
Suppose that  is a multivalued nonexpansive mapping that satisfies Condition I. Let
is a multivalued nonexpansive mapping that satisfies Condition I. Let  be the sequence of Ishikawa iterates defined by (3.12). Assume that
be the sequence of Ishikawa iterates defined by (3.12). Assume that  satisfying
satisfying  for any fixed point
for any fixed point  and
and  Then the sequence
Then the sequence  strongly converges to a fixed point of
strongly converges to a fixed point of 
Proof.
Similar to the proof of Theorem 5.2, we obtain  exists for each
exists for each  and
and

Then

This implies

Thus,  and hence
and hence  Since
Since 

Therefore,  Furthermore Condition I implies
Furthermore Condition I implies

The proof of remaining part closely follows the proof of [2, Theorem 3.8], simply replacing  with
with  .
.
References
Sastry KPR, Babu GVR: Convergence of Ishikawa iterates for a multi-valued mapping with a fixed point. Czechoslovak Mathematical Journal 2005,55(4):817–826. 10.1007/s10587-005-0068-z
Panyanak B: Mann and Ishikawa iterative processes for multivalued mappings in Banach spaces. Computers & Mathematics with Applications 2007,54(6):872–877. 10.1016/j.camwa.2007.03.012
Song Y, Wang H: Convergence of iterative algorithms for multivalued mappings in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,70(4):1547–1556. 10.1016/j.na.2008.02.034
Song Y, Wang H: Erratum to "Mann and Ishikawa iterative processes for multivalued mappings in Banach spaces" [Comput. Math. Appl. 54 (2007) 872–877]. Computers & Mathematics with Applications 2008,55(12):2999–3002. 10.1016/j.camwa.2007.11.042
Nadler SB Jr.: Multi-valued contraction mappings. Pacific Journal of Mathematics 1969, 30: 475–488.
Assad NA, Kirk WA: Fixed point theorems for set-valued mappings of contractive type. Pacific Journal of Mathematics 1972,43(3):553–562.
Senter HF, Dotson WG Jr.: Approximating fixed points of nonexpansive mappings. Proceedings of the American Mathematical Society 1974,44(2):375–380. 10.1090/S0002-9939-1974-0346608-8
Bridson MR, Haefliger A: Metric Spaces of Non-Positive Curvature, Fundamental Principles of Mathematical Sciences. Volume 319. Springer, Berlin, Germany; 1999:xxii+643.
Brown KS: Buildings. Springer, New York, NY, USA; 1989:viii+215.
Goebel K, Reich S: Uniform Convexity, Hyperbolic Geometry, and Nonexpansive Mappings, Monographs and Textbooks in Pure and Applied Mathematics. Volume 83. Marcel Dekker, New York, NY, USA; 1984:ix+170.
Burago D, Burago Y, Ivanov S: A Course in Metric Geometry, Graduate Studies in Mathematics. Volume 33. American Mathematical Society, Providence, RI, USA; 2001:xiv+415.
Gromov M: Metric Structures for Riemannian and Non-Riemannian Spaces, Progress in Mathematics. Volume 152. Birkhäuser, Boston, Mass, USA; 1999:xx+585.
Kirk WA: Geodesic geometry and fixed point theory. In Seminar of Mathematical Analysis (Malaga/Seville, 2002/2003), Colección Abierta. Volume 64. Universidad de Sevilla, Secretariado de Publicaciones, Sevilla, Spain; 2003:195–225.
Kirk WA: Geodesic geometry and fixed point theory. II. In International Conference on Fixed Point Theory and Applications. Yokohama Publishers, Yokohama, Japan; 2004:113–142.
Kirk WA: Fixed point theorems in CAT(0) spaces and
 -trees. Fixed Point Theory and Applications 2004,2004(4):309–316.
-trees. Fixed Point Theory and Applications 2004,2004(4):309–316.Dhompongsa S, Kaewkhao A, Panyanak B: Lim's theorems for multivalued mappings in CAT(0) spaces. Journal of Mathematical Analysis and Applications 2005,312(2):478–487. 10.1016/j.jmaa.2005.03.055
Dhompongsa S, Kirk WA, Panyanak B: Nonexpansive set-valued mappings in metric and Banach spaces. Journal of Nonlinear and Convex Analysis 2007,8(1):35–45.
Dhompongsa S, Kirk WA, Sims B: Fixed points of uniformly Lipschitzian mappings. Nonlinear Analysis: Theory, Methods & Applications 2006,65(4):762–772. 10.1016/j.na.2005.09.044
Chaoha P, Phon-on A: A note on fixed point sets in CAT(0) spaces. Journal of Mathematical Analysis and Applications 2006,320(2):983–987. 10.1016/j.jmaa.2005.08.006
Fujiwara K, Nagano K, Shioya T: Fixed point sets of parabolic isometries of CAT(0)-spaces. Commentarii Mathematici Helvetici 2006,81(2):305–335.
Leustean L: A quadratic rate of asymptotic regularity for CAT(0)-spaces. Journal of Mathematical Analysis and Applications 2007,325(1):386–399. 10.1016/j.jmaa.2006.01.081
Shahzad N, Markin J: Invariant approximations for commuting mappings in CAT(0) and hyperconvex spaces. Journal of Mathematical Analysis and Applications 2008,337(2):1457–1464. 10.1016/j.jmaa.2007.04.041
Kirk WA, Panyanak B: A concept of convergence in geodesic spaces. Nonlinear Analysis: Theory, Methods & Applications 2008,68(12):3689–3696. 10.1016/j.na.2007.04.011
Dhompongsa S, Panyanak B: On
 -convergence theorems in CAT(0) spaces. Computers & Mathematics with Applications 2008,56(10):2572–2579. 10.1016/j.camwa.2008.05.036
-convergence theorems in CAT(0) spaces. Computers & Mathematics with Applications 2008,56(10):2572–2579. 10.1016/j.camwa.2008.05.036Bruhat F, Tits J: Groupes réductifs sur un corps local. Publications Mathématiques de L'IHÉS 1972,41(1):5–251.
Opial Z: Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bulletin of the American Mathematical Society 1967, 73: 591–597. 10.1090/S0002-9904-1967-11761-0
Suzuki T: Strong convergence theorems for infinite families of nonexpansive mappings in general Banach spaces. Fixed Point Theory and Applications 2005,2005(1):103–123.
Acknowledgments
We are grateful to Professor Sompong Dhompongsa for his suggestion and advice during the preparation of the article. The research was supported by the Commission on Higher Education and Thailand Research Fund under Grant MRG5080188.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Laowang, W., Panyanak, B. Strong and  Convergence Theorems for Multivalued Mappings in
Convergence Theorems for Multivalued Mappings in  Spaces.
J Inequal Appl 2009, 730132 (2009). https://doi.org/10.1155/2009/730132
Spaces.
J Inequal Appl 2009, 730132 (2009). https://doi.org/10.1155/2009/730132
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/730132


 is such that
is such that 

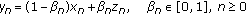
 Spaces
Spaces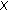 is a CAT (0) space;
is a CAT (0) space;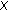 satisfies (CN);
satisfies (CN); satisfies (2.5).
satisfies (2.5). Convergence of Mann Iteration
Convergence of Mann Iteration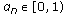 and
and 
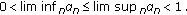
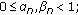
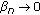 as
as 
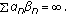


 -trees. Fixed Point Theory and Applications 2004,2004(4):309–316.
-trees. Fixed Point Theory and Applications 2004,2004(4):309–316. -convergence theorems in CAT(0) spaces. Computers & Mathematics with Applications 2008,56(10):2572–2579. 10.1016/j.camwa.2008.05.036
-convergence theorems in CAT(0) spaces. Computers & Mathematics with Applications 2008,56(10):2572–2579. 10.1016/j.camwa.2008.05.036