- Research Article
- Open access
- Published:
On Generalized Paranormed Statistically Convergent Sequence Spaces Defined by Orlicz Function
Journal of Inequalities and Applications volume 2009, Article number: 729045 (2009)
Abstract
We define generalized paranormed sequence spaces  ,
,  ,
,  , and
, and  defined over a seminormed sequence space
defined over a seminormed sequence space  . We establish some inclusion relations between these spaces under some conditions.
. We establish some inclusion relations between these spaces under some conditions.
1. Introduction

will represent the spaces of all, convergent, null, statistically convergent, statistically null, bounded, bounded statistically convergent, and bounded statistically null  -valued sequence spaces throughout the paper, where
-valued sequence spaces throughout the paper, where  is a seminormed space, seminormed by
is a seminormed space, seminormed by  For
For  the space of complex numbers, these spaces represent the
the space of complex numbers, these spaces represent the  which are the spaces of all, convergent, null, statistically convergent, statistically null, bounded, bounded statistically convergent, and bounded statistically null sequences, respectively. The zero sequence is denoted by
which are the spaces of all, convergent, null, statistically convergent, statistically null, bounded, bounded statistically convergent, and bounded statistically null sequences, respectively. The zero sequence is denoted by  , where
, where  is the zero element of
is the zero element of  .
.
The idea of statistical convergence was introduced by Fast [1] and studied by various authors (see [2–4]). The notion depends on the density of subsets of the set  of natural numbers. A subset
of natural numbers. A subset  of
of  is said to have density
is said to have density  if
if

where  is the characteristic function of
is the characteristic function of  .
.
A sequence  is said to be statistically convergent to the number
is said to be statistically convergent to the number  (i.e.,
(i.e.,  ) if for every
) if for every 

In this case, we write  or stat
or stat  lim
lim 
Let  be a mapping of the set of positive integers into itself. A continuous linear functional
be a mapping of the set of positive integers into itself. A continuous linear functional  on
on  , the space of real bounded sequences, is said to be an invariant mean or
, the space of real bounded sequences, is said to be an invariant mean or  -mean if and only if
-mean if and only if
(1) when the sequence
when the sequence  has
has  for all
for all  ,
,
(2) , where
, where 
(3) for all
for all 
The mappings  are one to one and such that
are one to one and such that  for all positive integers
for all positive integers  and
and  where
where  denotes the
denotes the  th iterate of the mapping
th iterate of the mapping  at
at  . Thus
. Thus  extends the limit functional on
extends the limit functional on  , the space of convergent sequences, in the sense that
, the space of convergent sequences, in the sense that  for all
for all  . In that case
. In that case  is translation mapping
is translation mapping  , a
, a  -mean is often called a Banach limit, and
-mean is often called a Banach limit, and  , the set of bounded sequences all of whose invariant means are equal, is the set of almost convergent sequences [5].
, the set of bounded sequences all of whose invariant means are equal, is the set of almost convergent sequences [5].
If  , set
, set  It can be shown [6] that
It can be shown [6] that

where 
Several authors including Schaefer [7], Mursaleen [6], Sava [8], and others have studied invariant convergent sequences.
[8], and others have studied invariant convergent sequences.
An Orlicz function is a function  , which is continuous, nondecreasing, and convex with
, which is continuous, nondecreasing, and convex with  for
for  and
and  as
as  . If the convexity of an Orlicz function
. If the convexity of an Orlicz function  is replaced by
is replaced by

then this function is called modulus function, introduced and investigated by Nakano [9] and followed by Ruckle [10], Maddox [11], and many others.
Lindenstrauss and Tzafriri [12] used the idea of Orlicz function to construct the sequence space

which is called an Orlicz sequence space.
The space  becomes a Banach space with the norm
becomes a Banach space with the norm

The space  is closely related to the space
is closely related to the space  which is an Orlicz sequence space with
which is an Orlicz sequence space with  for
for  . Orlicz sequence spaces were introduced and studied by Parashar and Choudhary [13], Bhardwaj and Singh [14], and many others.
. Orlicz sequence spaces were introduced and studied by Parashar and Choudhary [13], Bhardwaj and Singh [14], and many others.
It is well known that since  is a convex function and
is a convex function and  then
then  for all
for all  with
with  .
.
An Orlicz funtion  is said to satisfy
is said to satisfy  -condition for all values of
-condition for all values of  , if there exists constant
, if there exists constant  , such that
, such that  . The
. The  -condition is equivalent to the inequality
-condition is equivalent to the inequality  for all values of
for all values of  and for
and for  being satisfied [15].
being satisfied [15].
The notion of paranormed space was introduced by Nakano [16] and Simons [17]. Later on it was investigated by Maddox [18], Lascarides [19], Rath and Tripathy [20], Tripathy and Sen [21], Tripathy [22], and many others.
The following inequality will be used throughout this paper. Let  be a sequence of positive real numbers with
be a sequence of positive real numbers with  and let
and let  . Then for
. Then for  , the set of complex numbers for all
, the set of complex numbers for all  , we have [23]
, we have [23]

2. Definitions and Notations
A sequence space  is said to be solid (or normal) if
is said to be solid (or normal) if  , whenever
, whenever  and for all sequences
and for all sequences  of scalars with
of scalars with  for all
for all  .
.
A sequence space  is said to be symmetric if
is said to be symmetric if  implies
implies  , where
, where  is a permutation of
is a permutation of  .
.
A sequence space  is said to be monotone if it contains the canonical preimages of its step spaces.
is said to be monotone if it contains the canonical preimages of its step spaces.
Throughout the paper  will represent a sequence of positive real numbers and
will represent a sequence of positive real numbers and  a seminormed space over the field
a seminormed space over the field  of complex numbers with the seminorm
of complex numbers with the seminorm  . We define the following sequence spaces:
. We define the following sequence spaces:

We write

If  ,
,  for each
for each  and
and  then these spaces reduce to the spaces
then these spaces reduce to the spaces

defined by Tripathy and Sen [21].
Firstly, we give some results; those will help in establishing the results of this paper.
Lemma 2.1 ([21]).
For two sequences  and
and  one has
one has  if and only if
if and only if  , where
, where  such that
such that 
Lemma 2.2 ([21]).
Let  and
and  , then the followings are equivalent:
, then the followings are equivalent:
(i) and
and 
(ii)
Lemma 2.3 ([21]).
Let  be an infinite subset of
be an infinite subset of  such that
such that  Let
Let

Then  is uncountable.
is uncountable.
Lemma 2.4 ([24]).
If a sequence space  is solid then
is solid then  is monotone.
is monotone.
3. Main Results
Theorem 3.1.

,  ,
,  ,
,  are linear spaces.
are linear spaces.
Proof.
Let  . Then there exist
. Then there exist  ,
,  positive real numbers and
positive real numbers and  ,
,  such that
such that

Let  ,
,  be scalars and let
be scalars and let  . Then by (1.7) we have
. Then by (1.7) we have

Hence  is a linear space.
is a linear space.
The rest of the cases will follow similarly.
Theorem 3.2.
The spaces  and
and  are paranormed spaces, paranormed by
are paranormed spaces, paranormed by

where  .
.
Proof.
We prove the theorem for the space  . The proof for the other space can be proved by the same way. Clearly
. The proof for the other space can be proved by the same way. Clearly  for all
for all  and
and  . Let
. Let  Then we have
Then we have  ,
,  such that
such that

Let  . Then by the convexity of
. Then by the convexity of  , we have
, we have

Hence from above inequality, we have

For the continuity of scalar multiplication let  be any complex number. Then by the definition of
be any complex number. Then by the definition of  we have
we have

where  .
.
Since  we have
we have  Then
Then

and therefore  converges to zero when
converges to zero when  converges to zero or
converges to zero or  converges to zero.
converges to zero.
Hence the spaces  and
and  are paranormed by
are paranormed by  .
.
Theorem 3.3.
Let  be complete seminormed space, then the spaces
be complete seminormed space, then the spaces  and
and  are complete.
are complete.
Proof.
We prove it for the case  and the other case can be established similarly. Let
and the other case can be established similarly. Let  be a Cauchy sequence in
be a Cauchy sequence in  for all
for all  . Then
. Then  , as
, as  . For a given
. For a given  , let
, let  and
and  to be such that
to be such that  . Then there exists a positive integer
. Then there exists a positive integer  such that
such that

Using definition of paranorm we get

Hence  is a Cauchy sequence in
is a Cauchy sequence in  . Therefore for each
. Therefore for each  there exists a positive integer
there exists a positive integer  such that
such that

Using continuity of  , we find that
, we find that

Thus

Taking infimum of such  s we get
s we get

for all  and
and  . Since
. Since  and
and  is continuous, it follows that
is continuous, it follows that  . This completes the proof of the theorem.
. This completes the proof of the theorem.
Theorem 3.4.
Let  and
and  be two Orlicz functions satisfying
be two Orlicz functions satisfying  -condition. Then
-condition. Then
(i)
(ii)
where  ,
,  ,
,  and
and  .
.
Proof.
-
(i)
We prove this part for
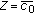 and the rest of the cases will follow similarly. Let
and the rest of the cases will follow similarly. Let  . Then for a given
. Then for a given  , there exists
, there exists 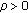 such that there exists a subset
such that there exists a subset 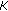 of
of  with
with  , where
, where  (3.15)
(3.15)
If we take  then
then  implies that
implies that  . Hence we have by convexity of
. Hence we have by convexity of 

Thus

Hence by (3.15) it follows that for a given  , there exists
, there exists  such that
such that

Therefore 
-
(ii)
We prove this part for the case
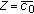 and the other cases will follow similarly.
and the other cases will follow similarly.
Let  . Then by using (1.7) it can be shown that
. Then by using (1.7) it can be shown that  . Hence
. Hence

This completes the proof.
Theorem 3.5.
For any sequence  of positive real numbers and for any two seminorms
of positive real numbers and for any two seminorms  and
and  on
on  one has
one has

where  ,
,  ,
,  and
and  .
.
Proof.
The proof follows from the fact that the zero sequence belongs to each of the classes the sequence spaces involved in the intersection.
The proof of the following result is easy, so omitted.
Proposition 3.6.
Let  be an Orlicz function which satisfies
be an Orlicz function which satisfies condition, and let
condition, and let  and
and  be two seminorms on
be two seminorms on  . Then
. Then
(i)
(ii)
(iii) where
where  ,
,  ,
,  , and
, and  ,
,
(iv)if  is stronger than
is stronger than  , then
, then

where  ,
,  ,
,  and
and  .
.
Theorem 3.7.
The spaces  are not solid, where
are not solid, where  and
and  .
.
Proof.
To show that the spaces are not solid in general, consider the following example. Let  ,
,  for all
for all  ,
,  , where
, where  and
and  for all
for all  . Then we have
. Then we have  for all
for all  . Consider the sequence
. Consider the sequence  , where
, where  is defined by
is defined by  and
and  for each fixed
for each fixed  . Hence
. Hence  for
for  and
and  . Let
. Let  if
if  is odd and
is odd and  , otherwise. Then
, otherwise. Then  for
for  and
and  . Thus
. Thus  is not solid for
is not solid for  and
and  .
.
The proof of the following result is obvious in view of Lemma 2.4.
Proposition 3.8.
The space  is solid as well as monotone for
is solid as well as monotone for  and
and  .
.
Theorem 3.9.
The spaces  are not symmetric, where
are not symmetric, where  ,
,  ,
,  and
and  .
.
Proof.
To show that the spaces are not symmetric, consider the following examples. Let  ,
,  for all
for all  ,
,  , where
, where  and
and  for all
for all  . Then we have
. Then we have  for all
for all  . We consider the sequence
. We consider the sequence  defined by
defined by  if
if  and
and  otherwise. Then
otherwise. Then  for
for  and
and  . Let
. Let  be a rearrangement of
be a rearrangement of  , which is defined as
, which is defined as  if
if  is odd and
is odd and  , otherwise. Then
, otherwise. Then  for
for  and
and  .
.
To show for  and
and  , let
, let  for all
for all  odd and
odd and  for all
for all  even. Let
even. Let  and
and  , where
, where  . Let
. Let  and
and  for all
for all  . Then we have
. Then we have  for all
for all  . We consider
. We consider

Then  for
for  and
and  . We consider the rearrengement
. We consider the rearrengement  of
of  as
as

Then  for
for  and
and  . Thus the spaces
. Thus the spaces  are not symmetric in general, where
are not symmetric in general, where  ,
,  ,
,  and
and  .
.
Proposition 3.10.
For two sequences  and
and  one has
one has  if and only if
if and only if  , where
, where  such that
such that  .
.
Proof.
The proof is obvious in view of Lemma 2.1.
The following result is a consequence of the above result.
Corollary 3.11.
For two sequences  and
and  one has
one has  if and only if
if and only if  and
and  , where
, where  such that
such that  .
.
The following result is obvious in view of Lemma 2.2.
Proposition 3.12.
Let  and
and  , then the followings are equivalent:
, then the followings are equivalent:
(i) and
and 
(ii)
Theorem 3.13.
Let  be a sequence of nonnegative bounded real numbers such that
be a sequence of nonnegative bounded real numbers such that  Then
Then

Proof.
Let  . Then for a given
. Then for a given  , we have
, we have

where the vertical bar indicates the number of elements in the enclosed set.
From the above inequality it follows that  .
.
Conversely let  . Let
. Let  such that
such that

For a given  , let
, let  .
.
Let  .
.
Since  , so
, so  , uniformly in
, uniformly in  , as
, as  . There exits a positive integer
. There exits a positive integer  such that
such that  for all
for all  . Then for all
. Then for all  , we have
, we have

Hence  .
.
This completes the proof of the theorem.
The following result is a consequence of the above theorem.
Corollary 3.14.
Let  and
and  be two bounded sequences of real numbers such that
be two bounded sequences of real numbers such that  and
and  Then
Then

Since the inclusion relations  and
and  are strict, we have the following result.
are strict, we have the following result.
Corollary 3.15.
The spaces  and
and  are nowhere dense subsets of
are nowhere dense subsets of 
The following result is obvious in view of Lemma 2.3.
Proposition 3.16.
The spaces  and
and  are not separable.
are not separable.
References
Fast H: Sur la convergence statistique. Colloquium Mathematicum 1951, 2: 241–244.
Connor JS: The statistical and strong
 -Cesàro convergence of sequences. Analysis 1988,8(1–2):47–63.
-Cesàro convergence of sequences. Analysis 1988,8(1–2):47–63.Fridy JA: On statistical convergence. Analysis 1985,5(4):301–313.
Šalát T: On statistically convergent sequences of real numbers. Mathematica Slovaca 1980,30(2):139–150.
Lorentz GG: A contribution to the theory of divergent sequences. Acta Mathematica 1948, 80: 167–190. 10.1007/BF02393648
Mursaleen : Invariant means and some matrix transformations. Tamkang Journal of Mathematics 1979,10(2):183–188.
Schaefer P: Infinite matrices and invariant means. Proceedings of the American Mathematical Society 1972, 36: 104–110. 10.1090/S0002-9939-1972-0306763-0
Savaş E: On lacunary strong
 -convergence. Indian Journal of Pure and Applied Mathematics 1990,21(4):359–365.
-convergence. Indian Journal of Pure and Applied Mathematics 1990,21(4):359–365.Nakano H: Concave modulars. Journal of the Mathematical Society of Japan 1953, 5: 29–49. 10.2969/jmsj/00510029
Ruckle WH:
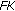 spaces in which the sequence of coordinate vectors is bounded. Canadian Journal of Mathematics 1973, 25: 973–978. 10.4153/CJM-1973-102-9
spaces in which the sequence of coordinate vectors is bounded. Canadian Journal of Mathematics 1973, 25: 973–978. 10.4153/CJM-1973-102-9Maddox IJ: Sequence spaces defined by a modulus. Mathematical Proceedings of the Cambridge Philosophical Society 1986,100(1):161–166. 10.1017/S0305004100065968
Lindenstrauss J, Tzafriri L: On Orlicz sequence spaces. Israel Journal of Mathematics 1971, 10: 379–390. 10.1007/BF02771656
Parashar SD, Choudhary B: Sequence spaces defined by Orlicz functions. Indian Journal of Pure and Applied Mathematics 1994,25(4):419–428.
Bhardwaj VK, Singh N: On some new spaces of lacunary strongly
 -convergent sequences defined by Orlicz functions. Indian Journal of Pure and Applied Mathematics 2000,31(11):1515–1526.
-convergent sequences defined by Orlicz functions. Indian Journal of Pure and Applied Mathematics 2000,31(11):1515–1526.Krasnoselskii MA, Rutitsky YB: Convex Functions and Orlicz Spaces. P. Noordhoff, Groningen, The Netherlands; 1961:xi+249.
Nakano H: Modulared sequence spaces. Proceedings of the Japan Academy 1951, 27: 508–512. 10.3792/pja/1195571225
Simons S: The sequence spaces
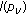 and
and 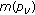 . Proceedings of the London Mathematical Society 1965, 15: 422–436. 10.1112/plms/s3-15.1.422
. Proceedings of the London Mathematical Society 1965, 15: 422–436. 10.1112/plms/s3-15.1.422Maddox IJ: Paranormed sequence spaces generated by infinite matrices. Mathematical Proceedings of the Cambridge Philosophical Society 1968, 64: 335–340. 10.1017/S0305004100042894
Lascarides CG: A study of certain sequence spaces of Maddox and a generalization of a theorem of Iyer. Pacific Journal of Mathematics 1971, 38: 487–500.
Rath D, Tripathy BC: Matrix maps on sequence spaces associated with sets of integers. Indian Journal of Pure and Applied Mathematics 1996,27(2):197–206.
Tripathy BC, Sen M: On generalized statistically convergent sequences. Indian Journal of Pure and Applied Mathematics 2001,32(11):1689–1694.
Tripathy BC: On generalized difference paranormed statistically convergent sequences. Indian Journal of Pure and Applied Mathematics 2004,35(5):655–663.
Maddox IJ: Spaces of strongly summable sequences. The Quarterly Journal of Mathematics 1967, 18: 345–355. 10.1093/qmath/18.1.345
Kampthan PK, Gupta M: Sequence Spaces and Series. Marcel Dekkar, New York, NY, USA; 1980.
Acknowledgment
The authors would like to express their gratitude to the reviewers for their careful reading and valuable suggestions which improved the presentation of the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Başarir, M., Altundağ, S. On Generalized Paranormed Statistically Convergent Sequence Spaces Defined by Orlicz Function. J Inequal Appl 2009, 729045 (2009). https://doi.org/10.1155/2009/729045
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/729045
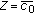 and the rest of the cases will follow similarly. Let
and the rest of the cases will follow similarly. Let  . Then for a given
. Then for a given  , there exists
, there exists 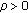 such that there exists a subset
such that there exists a subset 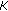 of
of  with
with  , where
, where 
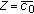 and the other cases will follow similarly.
and the other cases will follow similarly. -Cesàro convergence of sequences. Analysis 1988,8(1–2):47–63.
-Cesàro convergence of sequences. Analysis 1988,8(1–2):47–63. -convergence. Indian Journal of Pure and Applied Mathematics 1990,21(4):359–365.
-convergence. Indian Journal of Pure and Applied Mathematics 1990,21(4):359–365. spaces in which the sequence of coordinate vectors is bounded. Canadian Journal of Mathematics 1973, 25: 973–978. 10.4153/CJM-1973-102-9
spaces in which the sequence of coordinate vectors is bounded. Canadian Journal of Mathematics 1973, 25: 973–978. 10.4153/CJM-1973-102-9 -convergent sequences defined by Orlicz functions. Indian Journal of Pure and Applied Mathematics 2000,31(11):1515–1526.
-convergent sequences defined by Orlicz functions. Indian Journal of Pure and Applied Mathematics 2000,31(11):1515–1526.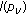 and
and 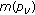 . Proceedings of the London Mathematical Society 1965, 15: 422–436. 10.1112/plms/s3-15.1.422
. Proceedings of the London Mathematical Society 1965, 15: 422–436. 10.1112/plms/s3-15.1.422