- Research Article
- Open access
- Published:
Monotonic and Logarithmically Convex Properties of a Function Involving Gamma Functions
Journal of Inequalities and Applications volume 2009, Article number: 728612 (2009)
Abstract
Using the series-expansion of digamma functions and other techniques, some monotonicity and logarithmical concavity involving the ratio of gamma function are obtained, which is to give a partially affirmative answer to an open problem posed by B.-N.Guo and F.Qi. Several inequalities for the geometric means of natural numbers are established.
1. Introduction
For real and positive values of  the Euler gamma function
the Euler gamma function  and its logarithmic derivative
and its logarithmic derivative  , the so-called digamma function, are defined as
, the so-called digamma function, are defined as

For extension of these functions to complex variables and for basic properties see [1].
In recent years, many monotonicity results and inequalities involving the Gamma and incomplete Gamma functions have been established. This article is stimulated by an open problem posed by Guo and Qi in [2]. The extensions and generalizations of this problem can be found in [3–5] and some references therein.
Using Stirling formula, for all nonnegative integers  , natural numbers
, natural numbers  and
and  , an upper bound of the quotient of two geometrical means of natural numbers was established in [4] as follows:
, an upper bound of the quotient of two geometrical means of natural numbers was established in [4] as follows:

and the following lower bound was appeared in [2, 5]:

Since  as a generalization of inequality (1.3), the following monotonicity result was obtained by Guo and Qi in [2]. The function
as a generalization of inequality (1.3), the following monotonicity result was obtained by Guo and Qi in [2]. The function

is decreasing with respect to  on
on  for fixed
for fixed  Hence, for positive real numbers
Hence, for positive real numbers  and
and  , we have
, we have

Recently, in [6], Qi and Sun proved that the function

is strictly increasing with respect to  for all
for all 
Now, we generalize the function in (1.4) as follows: for positive real numbers  and
and  ,
,  , let
, let

The aim of this paper is to discuss the monotonicity and logarithmical convexity of the function  with respect to parameter
with respect to parameter  .
.
For convenience of the readers, we recall the definitions and basic knowledge of convex function and logarithmically convex function.
Definition 1.1.
Let  be a convex set,
be a convex set,  is called a convex function on
is called a convex function on  if
if

for all  , and
, and  is called concave if
is called concave if  is convex.
is convex.
Definition 1.2.
Let  be a convex set,
be a convex set,  is called a logarithmically convex function on
is called a logarithmically convex function on  if
if  is convex on
is convex on  , and
, and  is called logarithmically concave if
is called logarithmically concave if  is concave.
is concave.
The following criterion for convexity of function was established by Fichtenholz in [7].
Proposition 1.3.
Let  be a convex set, if
be a convex set, if  have continuous second partial derivatives, then
have continuous second partial derivatives, then  is a convex (or concave) function on
is a convex (or concave) function on  if and only if
if and only if  is a positive (or negative) semidefinite matrix for all
is a positive (or negative) semidefinite matrix for all  , where
, where

and  for
for  ,
,  .
.
Notation.
In Definitions 1.1, 1.2 and Proposition 1.3, we denote  by the points (or vectors) of
by the points (or vectors) of  , and denote
, and denote  by the real variables in the later.
by the real variables in the later.
Our main results are Theorems 1.4 and 1.5.
Theorem 1.4.
-
(1)
For any fixed
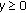 ,
, 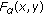 is strictly increasing (or decreasing, resp.) with respect to
is strictly increasing (or decreasing, resp.) with respect to  on
on 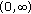 if and only if
if and only if  (or
(or 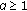 , resp.);
, resp.); -
(2)
For any fixed
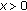 ,
, 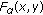 is strictly increasing with respect to
is strictly increasing with respect to 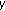 on
on 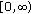 if and only if
if and only if  .
.
Theorem 1.5.
-
(1)
If
 , then
, then 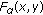 is logarithmically concave with respect to
is logarithmically concave with respect to  ;
; -
(2)
If
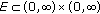 is a convex set with nonempty interior and
is a convex set with nonempty interior and 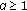 , then
, then  is neither logarithmically convex nor logarithmically concave with respect to
is neither logarithmically convex nor logarithmically concave with respect to 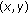 on
on 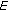 .
.
The following two corollaries can be derived from Theorems 1.4 and 1.5 immediately.
Corollary 1.6.
If  , then
, then

Remark 1.7.
Inequality (1.3) can be derived from Corollary 1.6 if we take  . Although we cannot get the inequality (1.2) exactly from Corollary 1.6, but we can get the following inequality which is close to inequality (1.2):
. Although we cannot get the inequality (1.2) exactly from Corollary 1.6, but we can get the following inequality which is close to inequality (1.2):

Corollary 1.8.
If  , then
, then

Remark 1.9.
We conjecture that the inequality (1.2) can be improved if we can choose two pairs of integers  and
and  properly.
properly.
2. Lemmas
It is well known that the Bernoulli numbers  is defined [8] in general by
is defined [8] in general by

In particular, we have

In [9], the following summation formula is given:

for nonnegative integer  , where
, where  denotes the Euler number, which implies
denotes the Euler number, which implies

Recently, the Bernoulli and Euler numbers and polynomials are generalized in [10–13]. The following two Lemmas were established by Qi and Guo in [3, 14].
Lemma 2.1 (see [3]).
For real number  and natural number
and natural number  , one has
, one has




Lemma 2.2 (see [14]).
Inequalities

,

hold in  for
for  .
.
Lemma 2.3.
Let  , then the following statements are true:
, then the following statements are true:
(1) if  , then
, then  for
for  ;
;
(2) if  , then
, then  for
for  .
.
Proof.
-
(1)
Making use of (2.6) we get
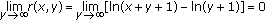 (2.11)
(2.11)
for any fixed  .
.
Since  and
and  , we have
, we have

for all  .
.
Therefore, Lemma 2.3(1) follows from (2.11) and (2.12).
-
(2)
If
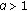 , then (2.12) leads to
, then (2.12) leads to 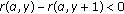 (2.13)
(2.13)
for  .
.
Therefore, Lemma 2.3(2) follows from (2.11) and (2.13).
Lemma 2.4.
If  , then
, then  for
for  .
.
Proof.
It is easy to see that

for all  .
.
Let  , then
, then



for  . On the other hand, from (2.10) we know that
. On the other hand, from (2.10) we know that  is strictly decreasing on
is strictly decreasing on  .
.
Therefore, Lemma 2.4 follows from (2.14)–(2.17).
Remark 2.5.
Let

Then simple computation shows that

Lemma 2.6.
Let  then the following statements are true:
then the following statements are true:
(1) if  , then
, then

for  ;
;
(2) if  then
then

for  .
.
Proof.
Let

Then it is not difficult to verify



-
(1)
If
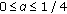 , then making use of Lemmas 2.2, 2.4 and (2.25) we get
, then making use of Lemmas 2.2, 2.4 and (2.25) we get 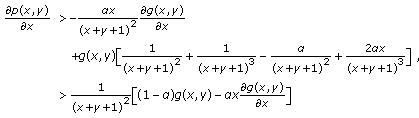 (2.26)
(2.26)
for  .
.
Let  ,
,  and
and  . Then simple computation leads to
. Then simple computation leads to




for all  .
.
It is well known that  , where
, where  is the Euler's constant. From this we get
is the Euler's constant. From this we get

From Lemma 2.2, (2.27)–(2.29), (2.31) and the assumption  , we conclude that
, we conclude that

Therefore, Lemma 2.6(1) follows from (2.23)–(2.26), (2.30), and (2.32).
-
(2)
If
 , then making use of (2.8), Lemma 2.4 and (2.25) we obtain
, then making use of (2.8), Lemma 2.4 and (2.25) we obtain 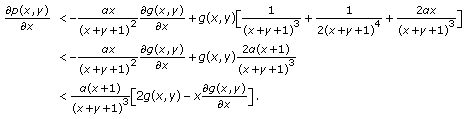 (2.33)
(2.33)
Let

Then

for  by Lemma 2.2, and
by Lemma 2.2, and

for  .
.
Therefore, Lemma 2.6(2) follows from (2.23)–(2.25) and (2.33)–(2.36).
3. Proofs of Theorems 1.4 and 1.5
Proof of Theorem 1.4.
-
(1)
Let
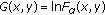 and
and 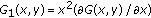 , then
, then  (3.1)
(3.1)
The following three cases will complete the proof of Theorem 1.4(1).
Case 1.
If  , then (3.1) and Lemma 2.2 imply
, then (3.1) and Lemma 2.2 imply

for  .
.
From (3.2) and the fact that  for all
for all  we know that
we know that  is strictly increasing with respect to
is strictly increasing with respect to  on
on  for any fixed
for any fixed  .
.
Case 2.
If  , then (3.1) and (2.7) imply
, then (3.1) and (2.7) imply

for  , where
, where  and
and  .
.
From (3.3) and the fact that  for all
for all  we know that
we know that  is strictly decreasing with respect to
is strictly decreasing with respect to  on
on  for any fixed
for any fixed  .
.
Case 3.
If  , let
, let

Then


for  .
.
It is obvious that (3.6) implies

The continuity of  with respect to
with respect to  for any fixed
for any fixed  and (3.7) imply that there exists
and (3.7) imply that there exists  such that
such that

for  .
.
From (3.5), (3.8) and  we know that
we know that  is strictly decreasing with respect to
is strictly decreasing with respect to  on
on  for
for  .
.
On the other hand, making use of (2.5) and (2.6) we have

where

for  and
and  .
.
Equation (3.9) implies that there exists  such that
such that

for  .
.
Hence, from (3.11) we know that  is strictly increasing with respect to
is strictly increasing with respect to  on
on  for
for  .
.
-
(2)
Since
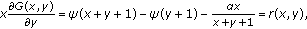 (3.12)
(3.12)
then, Theorem 1.4(2) follows from (3.12) and Lemma 2.3.
Proof of Theorem 1.5.
Let  and
and  , then simple calculation yields
, then simple calculation yields



where  , and
, and  are defined in Remark 2.5 and Lemma 2.6.
are defined in Remark 2.5 and Lemma 2.6.
According to the Definition 1.2 and Proposition 1.3, to prove Theorem 1.5 we need only to show that


for  and
and  , and
, and

for  and
and  .
.
Next, let  then
then


for  by Lemma 2.2 and
by Lemma 2.2 and  .
.
Therefore, (3.16) follows from (3.19) and (3.20), and (3.17) and (3.18) follow from Lemma 2.6. The proof of Theorem 1.5 is completed.
References
Whittaker ET, Watson GN: A Course of Modern Analysis, Cambridge Mathematical Library. Cambridge University Press, Cambridge, UK; 1996:vi+608.
Guo B-N, Qi F: Inequalities and monotonicity for the ratio of gamma functions. Taiwanese Journal of Mathematics 2003,7(2):239–247.
Qi F, Guo B-N: Monotonicity and convexity of ratio between gamma functions to different powers. Journal of the Indonesian Mathematical Society 2005,11(1):39–49.
Qi F: Inequalities and monotonicity of sequences involving
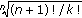 . Soochow Journal of Mathematics 2003,29(4):353–361.
. Soochow Journal of Mathematics 2003,29(4):353–361.Qi F, Luo Q-M: Generalization of H. Minc and L. Sathre's inequality. Tamkang Journal of Mathematics 2000,31(2):145–148.
Qi F, Sun J-S: A mononotonicity result of a function involving the gamma function. Analysis Mathematica 2006,32(4):279–282. 10.1007/s10476-006-0012-y
Fichtenholz GM: Differential- und Integralrechnung. II. VEB Deutscher Verlag der Wissenschaften, Berlin, Germany; 1966.
Abramowitz M, Stegun IA: Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, National Bureau of Standards Applied Mathematics Series. Volume 55. U.S.Government Printing Office, Washington, DC, USA; 1964:xiv+1046.
Wang Zh-X, Guo D-R: Introduction to Special Function, The Series of Advanced Physics of Peking University. Peking University Press, Beijing, China; 2000.
Guo B-N, Qi F: Generalization of Bernoulli polynomials. International Journal of Mathematical Education in Science and Technology 2002,33(3):428–431. 10.1080/002073902760047913
Luo Q-M, Guo B-N, Qi F, Debnath L: Generalizations of Bernoulli numbers and polynomials. International Journal of Mathematics and Mathematical Sciences 2003,2003(59):3769–3776. 10.1155/S0161171203112070
Luo Q-M, Qi F: Relationships between generalized Bernoulli numbers and polynomials and generalized Euler numbers and polynomials. Advanced Studies in Contemporary Mathematics (Kyungshang) 2003,7(1):11–18.
Luo Q-M, Qi F, Debnath L: Generalizations of Euler numbers and polynomials. International Journal of Mathematics and Mathematical Sciences 2003,2003(61):3893–3901. 10.1155/S016117120321108X
Qi F, Guo B-N: A new proof of complete monotonicity of a function involving psi function. RGMIA Research Report Collection 2008.,11(3, article 12):
Acknowledgments
This research is partly supported by 973 Project of China under grant 2006CB708304, N S Foundation of China under Grant 10771195, and N S Foundation Zhejiang Province under Grant Y607128.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhao, TH., Chu, YM. & Jiang, YP. Monotonic and Logarithmically Convex Properties of a Function Involving Gamma Functions. J Inequal Appl 2009, 728612 (2009). https://doi.org/10.1155/2009/728612
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/728612
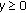 ,
, 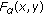 is strictly increasing (or decreasing, resp.) with respect to
is strictly increasing (or decreasing, resp.) with respect to  on
on 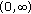 if and only if
if and only if  (or
(or 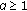 , resp.);
, resp.);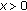 ,
, 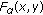 is strictly increasing with respect to
is strictly increasing with respect to 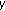 on
on 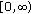 if and only if
if and only if  .
. , then
, then 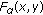 is logarithmically concave with respect to
is logarithmically concave with respect to  ;
;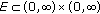 is a convex set with nonempty interior and
is a convex set with nonempty interior and 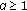 , then
, then  is neither logarithmically convex nor logarithmically concave with respect to
is neither logarithmically convex nor logarithmically concave with respect to 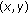 on
on 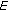 .
.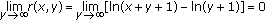
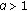 , then (2.12) leads to
, then (2.12) leads to 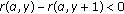
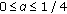 , then making use of Lemmas 2.2, 2.4 and (2.25) we get
, then making use of Lemmas 2.2, 2.4 and (2.25) we get 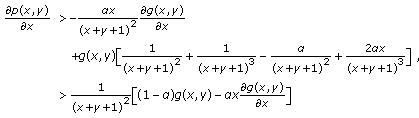
 , then making use of (2.8), Lemma 2.4 and (2.25) we obtain
, then making use of (2.8), Lemma 2.4 and (2.25) we obtain 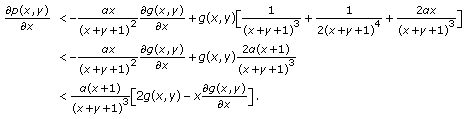
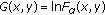 and
and 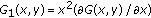 , then
, then 
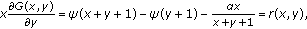
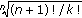 . Soochow Journal of Mathematics 2003,29(4):353–361.
. Soochow Journal of Mathematics 2003,29(4):353–361.