- Research Article
- Open access
- Published:
Admissible Estimators in the General Multivariate Linear Model with Respect to Inequality Restricted Parameter Set
Journal of Inequalities and Applications volume 2009, Article number: 718927 (2009)
Abstract
By using the methods of linear algebra and matrix inequality theory, we obtain the characterization of admissible estimators in the general multivariate linear model with respect to inequality restricted parameter set. In the classes of homogeneous and general linear estimators, the necessary and suffcient conditions that the estimators of regression coeffcient function are admissible are established.
1. Introduction
Throughout this paper,  , and
, and  denote the set of
denote the set of  real matrices, the subset of
real matrices, the subset of  consisting of symmetric matrices, and the subset of
consisting of symmetric matrices, and the subset of  consisting of nonnegative definite matrices, respectively. The symbols
consisting of nonnegative definite matrices, respectively. The symbols  , and
, and  stand for the transpose, the range, Moore-Penrose inverse, generalized inverse, and trace of
stand for the transpose, the range, Moore-Penrose inverse, generalized inverse, and trace of  , respectively. For any
, respectively. For any  ,
,  means
means  .
.
Consider the general multivariate linear model with respect to inequality restricted parameter set:

where  is an observable random matrix,
is an observable random matrix,  ,
,  ,
,  and
and  are known matrices, respectively.
are known matrices, respectively.  ,
,  (
( ) are unknown matrices.
) are unknown matrices.  is the error matrix.
is the error matrix.  denotes the vector made of the columns of
denotes the vector made of the columns of  and
and  denotes the Kronecker product.
denotes the Kronecker product.
Let  . For the linear function
. For the linear function  , we use the following matrix loss function:
, we use the following matrix loss function:

where  is a linear estimator of
is a linear estimator of  . The risk function is the expected value of loss function:
. The risk function is the expected value of loss function:

Suppose  and
and  are two estimators of
are two estimators of  , if for any
, if for any  , we have
, we have

and there exists  , such that
, such that  , then
, then  is said to be better than
is said to be better than  . If there does not exist any estimator in set
. If there does not exist any estimator in set  that is better than
that is better than  , where parameters
, where parameters  , then
, then  is called the admissible estimator of
is called the admissible estimator of  in the set
in the set  . We denote it by
. We denote it by  .
.
In the case of  , model (1.1) degenerates to the general multivariate linear model without restrictions. Under the quadratic loss function, many articles discussed the admissibility of linear estimators, such as Cohen [1], Rao [2], LaMotte [3], etc. Under the matrix loss function, Zhu and Lu [4] and Baksalary and Markiewicz [5] studied the admissibility of linear estimators when
, model (1.1) degenerates to the general multivariate linear model without restrictions. Under the quadratic loss function, many articles discussed the admissibility of linear estimators, such as Cohen [1], Rao [2], LaMotte [3], etc. Under the matrix loss function, Zhu and Lu [4] and Baksalary and Markiewicz [5] studied the admissibility of linear estimators when  respectively. Deng et al. [6] discussed the admissibility under the matrix loss in multivariate model. Markiewicz [7] discussed the admissibility in the general multivariate linear model. Marquardt [8] and Perlman [9] pointed out that the least square estimator is not still the admissible estimator if the parameters are restricted. Further, Groß and Markiewicz [10] pointed out that the admissible linear estimator has the form of ridge estimator if the parameters have no restrictions. Therefore, it is useful and important to discuss the admissibility of linear estimators when the parameters have some restrictions.
respectively. Deng et al. [6] discussed the admissibility under the matrix loss in multivariate model. Markiewicz [7] discussed the admissibility in the general multivariate linear model. Marquardt [8] and Perlman [9] pointed out that the least square estimator is not still the admissible estimator if the parameters are restricted. Further, Groß and Markiewicz [10] pointed out that the admissible linear estimator has the form of ridge estimator if the parameters have no restrictions. Therefore, it is useful and important to discuss the admissibility of linear estimators when the parameters have some restrictions.
Zhu and Zhang [11], Lu [12], Deng and Chen [13] studied the admissibility of linear estimators under the quadratic loss and matrix loss when  . Qin et al. [14] studied the admissibility of the estimators of estimable function under the loss function
. Qin et al. [14] studied the admissibility of the estimators of estimable function under the loss function  in multivariate linear model with respect to restricted parameter set when
in multivariate linear model with respect to restricted parameter set when  . In their case, whether an estimator is better than another or not does not depend on the regression parameters. It is easy to generalize the conclusions from univariate linear model to multivariate linear model. However under the matrix loss (1.2), it is more complicated. In this case, whether an estimator is better than another depends on the regression parameters.
. In their case, whether an estimator is better than another or not does not depend on the regression parameters. It is easy to generalize the conclusions from univariate linear model to multivariate linear model. However under the matrix loss (1.2), it is more complicated. In this case, whether an estimator is better than another depends on the regression parameters.
In this paper, using the methods of linear algebra and matrix theory, we discuss the admissibility of linear estimators in model (1.1) under the matrix loss (1.2). We prove that the admissibility of the estimators of estimable function under univariate linear model and multivariate linear model are equivalent in the class of homogeneous linear estimators, and some sufficient and necessary conditions that the estimators in the general multivariate linear model with respect to restricted parameter set are admissible are obtained whether the function of parameter is estimable or not, which enriches the theory of admissibility in multivariate linear model.
2. Main Results
Let  denote the class of homogeneous linear estimators, and let
denote the class of homogeneous linear estimators, and let  denote the class of general linear estimators.
denote the class of general linear estimators.
Lemma 2.1.
Under model (1.1) with the loss function (1.2), suppose  is an estimator of
is an estimator of  , one has
, one has

The equality holds if and only if

where  .
.
Proof.
Since

It is easy to verify that (2.1) holds, and the equality holds if and only if

Expanding it, we have

Thus  , that is
, that is  .
.
Lemma 2.2.
Under model (1.1) with the loss function (1.2), if  , suppose
, suppose  are estimators of
are estimators of  , then
, then  is better than
is better than  if and only if
if and only if


and the two equalities above cannot hold simultaneously.
Proof.
Since  ,
,  ,
,  , (2.3) implies the sufficiency is true. Suppose
, (2.3) implies the sufficiency is true. Suppose  is better than
is better than  , then for any
, then for any  , we have
, we have

and there exists some  such that the equality in (2.8) cannot hold. Taking
such that the equality in (2.8) cannot hold. Taking  in (2.8), (2.6) follows. Let
in (2.8), (2.6) follows. Let  ,
,  is the identity matrix, then for any
is the identity matrix, then for any  ,
,  , by (2.8), we have
, by (2.8), we have

Therefore, (2.7) holds. It is obvious that the two equalities in (2.6) and (2.7) cannot hold simultaneously.
Consider univariate linear model with respect to restricted parameter set:

and the loss function

where  ,
,  ,
,  and
and  are as defined in (1.1) and (1.2),
are as defined in (1.1) and (1.2),  and
and  are unknown parameters. Set
are unknown parameters. Set  . If
. If  is an admissible estimator of
is an admissible estimator of  , we denote it by
, we denote it by  .
.
Similarly to Lemma 2.2, we have the following lemma.
Lemma 2.3.
Under model (2.10) with the loss function (2.11), suppose  and
and  are estimators of
are estimators of  , then
, then  is better than
is better than  if and only if
if and only if


and the two equalities above cannot hold simultaneously.
Theorem 2.4.
Consider the model (1.1) with the loss function (1.2),  if and only if
if and only if  in model (2.10) with the loss function (2.11).
in model (2.10) with the loss function (2.11).
Proof.
From Lemmas 2.2 and 2.3, we need only to prove the equivalence of (2.7) and (2.13).
Suppose (2.7) is true, we can take  ,
,  , and plug it into (2.7). Then (2.13) follows.
, and plug it into (2.7). Then (2.13) follows.
For the inverse part, suppose (2.13) is true, let  , we have
, we have

The claim follows.
Remark 2.5.
From this Theorem, we can easily generalize the result under univariate linear model to the case under multivariate linear model in the class of homogeneous linear estimators.
Theorem 2.6.
Consider the model (1.1) with the loss function (1.2), if  is estimable, then
is estimable, then  if and only if:
if and only if:
(1) ,
,
(2)if there exists  , such that
, such that

then  ,
,  , where
, where  .
.
Proof.
From the corresponding theorem in article Deng and Chen [13], under the model (2.10) with the loss function (2.11), if  is estimable, then
is estimable, then  if and only if (1) and (2) in Theorem 2.6 are satisfied. Now Theorem 2.6 follows from Theorem 2.4.
if and only if (1) and (2) in Theorem 2.6 are satisfied. Now Theorem 2.6 follows from Theorem 2.4.
Lemma 2.7.
Consider the model (1.1) with the loss function (1.2), suppose  is an estimator of
is an estimator of  . One has
. One has

and the equality holds if and only if  .
.
Proof.
The proof follows from the following equalities:

Lemma 2.8.
Assume  , one has
, one has
(1)if  and
and  , then there exists
, then there exists  , for every
, for every  ,
,  and
and  .
.
(2) if and only if for any vector
if and only if for any vector  ,
,  implies
implies  .
.
Proof.
-
(1)
If
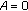 , the claim is trivial. If
, the claim is trivial. If 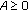 ,
,  , where
, where 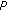 is an orthogonal matrix,
is an orthogonal matrix,  ,
,  . From
. From 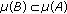 , we have
, we have 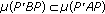 , notice that
, notice that  , we get
, we get  , where
, where  . Clearly, there exists
. Clearly, there exists  , such that
, such that  . Let
. Let  , then
, then  , and for every
, and for every 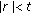 ,
,  , thus
, thus  and
and 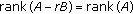 .
. -
(2)
The claim is easy to verify.
Theorem 2.9.
Consider the model (1.1) with the loss function (1.2), if  is estimable, then
is estimable, then  if and only if:
if and only if:
(1) ,
,
(2)if there exists  such that
such that

then  ,
,  and
and  , where
, where  .
.
Proof.
If  , by (2.17) we obtain
, by (2.17) we obtain  . Then
. Then  implies
implies  . The claim is true by Theorem 2.6. Now we assume
. The claim is true by Theorem 2.6. Now we assume  .
.
Necessity
Assume  , by Lemma 2.7, (1) is true. Now we will prove (2). Denote
, by Lemma 2.7, (1) is true. Now we will prove (2). Denote  ,
,  . Since
. Since  , rewrite (2.18) as the following
, rewrite (2.18) as the following

If there exists  such that (2.19) holds, for sufficient small
such that (2.19) holds, for sufficient small  , take
, take  . Since
. Since

Thus




In the above,  is sufficiently small,
is sufficiently small,  , thus (2.23) follows.
, thus (2.23) follows.  ,
,  ,
,  , thus (2.24) follows
, thus (2.24) follows

For any compatible vector  , assume
, assume

By (2.19) we obtain  , that is,
, that is,  , plug it into (2.26), then
, plug it into (2.26), then  ,
,  , thus
, thus

From Lemma 2.8, we have

Therefore, there exists  , for
, for  , the right side of (2.25) is nonnegative definite and its rank is
, the right side of (2.25) is nonnegative definite and its rank is  . If
. If  is small enough, for every
is small enough, for every  , we have
, we have  , and the equality cannot always hold if (2) does not hold. It contradicts
, and the equality cannot always hold if (2) does not hold. It contradicts  .
.
Sufficiency
Assume (1) and (2) are true. Since  , by Theorem 2.6,
, by Theorem 2.6,  . If there exists an estimator
. If there exists an estimator  that is better than
that is better than  , then for every
, then for every  ,
,

Note that for any  , if
, if  , then
, then  . Replace
. Replace  and
and  in (2.29) with
in (2.29) with  and
and  , respectively, divide by
, respectively, divide by  on both sides, and let
on both sides, and let  , we get
, we get

Since  , we have
, we have  and
and  (otherwise,
(otherwise,  is better than
is better than  ). Plug them into (2.29), for every
). Plug them into (2.29), for every  ,
,

Thus  and
and  .
.  implies
implies  , and the equality in (2.29) holds always. It contradicts that
, and the equality in (2.29) holds always. It contradicts that  is better than
is better than  .
.
Theorem 2.10.
Under model (1.1) and the loss function (1.2), if  is estimable, then
is estimable, then  if and only if
if and only if  .
.
Proof.
Denote  ,
,  , model (1.1) is transformed into
, model (1.1) is transformed into

Since

then (2.33) implies that  , which combining Theorem 2.4 and the fact that "if
, which combining Theorem 2.4 and the fact that "if  , then
, then  " yields
" yields  .
.
Corollary 2.11.
Under model (1.1) and the loss function (1.2), if  is estimable, then
is estimable, then  if and only if
if and only if  .
.
Lemma 2.12.
Consider model (1.1) with the loss function (1.2), suppose  , if
, if  , then
, then

Proof.

where  refers to the orthogonal projection onto
refers to the orthogonal projection onto  .
.
Lemma 2.13.
Suppose  and
and  are
are  and
and  real matrices, respectively, there exists a
real matrices, respectively, there exists a  matrix
matrix  such that
such that  if and only if
if and only if  and
and  .
.
Proof.
For the proof of sufficiency, we need only to prove that there exists a  such that
such that  is not an inverse symmetric matrix.
is not an inverse symmetric matrix.
Since  ,
,  .
.
(1)If there is  such that
such that  , take
, take  , then
, then

where  is the column vector whose only nonzero entry is a 1 in the
is the column vector whose only nonzero entry is a 1 in the  th position.
th position.
(2)If there does not exist  such that
such that  , then there must exist
, then there must exist  such that
such that  and
and  , take
, take  , then
, then

That is,  .
.
The proof is complete.
Theorem 2.14.
Consider the model (1.1) with the loss function (1.2), if  is inestimable, then
is inestimable, then  if and only if
if and only if  .
.
Proof.
Lemma 2.1 implies the necessity. For the proof of the inverse part, assume there exists  , for any
, for any  , we have
, we have

Since

where  , thus
, thus

where  is a known function. If there exists
is a known function. If there exists  such that
such that

note that  is inestimable, then
is inestimable, then  , by Lemma 2.13, there exists
, by Lemma 2.13, there exists  such that
such that

Take  ,
,  , since
, since  , so
, so  .
.
According to (2.40), we have for any real  ,
,

It is a contradiction. Therefore  . Since
. Since  , by Lemma 2.12, we obtain
, by Lemma 2.12, we obtain

Take  in (2.38), we have
in (2.38), we have

Thus  ,
,  . There is no estimator that is better than
. There is no estimator that is better than  in
in  .
.
Similarly to Theorem 2.14, we have the following theorem.
Theorem 2.15.
Under model (1.1) and the loss function (1.2), if  is inestimable, then
is inestimable, then  if and only if
if and only if  .
.
Remark 2.16.
This theorem indicates that if  is inestimable, then the admissibility of
is inestimable, then the admissibility of  has no relation with the choice of
has no relation with the choice of  owing to
owing to  .
.
References
Cohen A: All admissible linear estimates of the mean vector. Annals of Mathematical Statistics 1966, 37: 458–463. 10.1214/aoms/1177699528
Rao CR: Estimation of parameters in a linear model. The Annals of Statistics 1976,4(6):1023–1037. 10.1214/aos/1176343639
LaMotte LR: Admissibility in linear estimation. The Annals of Statistics 1982,10(1):245–255. 10.1214/aos/1176345707
Zhu XH, Lu CY: Admissibility of linear estimates of parameters in a linear model. Chinese Annals of Mathematics 1987,8(2):220–226.
Baksalary JK, Markiewicz A: A matrix inequality and admissibility of linear estimators with respect to the mean square error matrix criterion. Linear Algebra and Its Applications 1989, 112: 9–18. 10.1016/0024-3795(89)90584-3
Deng QR, Chen JB, Chen XZ: All admissible linear estimators of functions of the mean matrix in multivariate linear models. Acta Mathematica Scientia 1998,18(supplement):16–24.
Markiewicz A: Estimation and experiments comparison with respect to the matrix risk. Linear Algebra and Its Applications 2002, 354: 213–222. 10.1016/S0024-3795(01)00375-5
Marquardt DW: Generalized inverses, ridge regression, biased linear estimation and nonlinear estimation. Technometrics 1970, 12: 591–612. 10.2307/1267205
Perlman MD: Reduced mean square error estimation for several parameters. Sankhyā B 1972, 34: 89–92.
Groß J, Markiewicz A: Characterizations of admissible linear estimators in the linear model. Linear Algebra and Its Applications 2004, 388: 239–248.
Zhu XH, Zhang SL: Admissible linear estimators in linear models with constraints. Kexue Tongbao 1989,34(11):805–808.
Lu CY: Admissibility of inhomogeneous linear estimators in linear models with respect to incomplete ellipsoidal restrictions. Communications in Statistics. A 1995,24(7):1737–1742. 10.1080/03610929508831582
Deng QR, Chen JB: Admissibility of general linear estimators for incomplete restricted elliptic models under matrix loss. Chinese Annals of Mathematics 1997,18(1):33–40.
Qin H, Wu M, Peng JH: Universal admissibility of linear estimators in multivariate linear models with respect to a restricted parameter set. Acta Mathematica Scientia 2002,22(3):427–432.
Acknowledgments
The authors would like to thank the Editor Dr. Kunquan Lan and the anonymous referees whose work and comments made the paper more readable. The research was supported by National Science Foundation (60736047, 60772036, 10671007) and Foundation of BJTU (2006XM037), China.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, S., Liu, G. & Gui, W. Admissible Estimators in the General Multivariate Linear Model with Respect to Inequality Restricted Parameter Set. J Inequal Appl 2009, 718927 (2009). https://doi.org/10.1155/2009/718927
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/718927
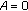 , the claim is trivial. If
, the claim is trivial. If 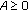 ,
,  , where
, where 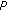 is an orthogonal matrix,
is an orthogonal matrix,  ,
,  . From
. From 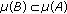 , we have
, we have 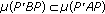 , notice that
, notice that  , we get
, we get  , where
, where  . Clearly, there exists
. Clearly, there exists  , such that
, such that  . Let
. Let  , then
, then  , and for every
, and for every 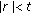 ,
,  , thus
, thus  and
and 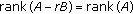 .
.