- Research Article
- Open access
- Published:
Superstability for Generalized Module Left Derivations and Generalized Module Derivations on a Banach Module (I)
Journal of Inequalities and Applications volume 2009, Article number: 718020 (2009)
Abstract
We discuss the superstability of generalized module left derivations and generalized module derivations on a Banach module. Let  be a Banach algebra and
be a Banach algebra and  a Banach
a Banach  -module,
-module,  and
and  . The mappings
. The mappings  , and
, and  are defined and it is proved that if
are defined and it is proved that if  (resp.,
(resp.,  is dominated by
is dominated by  then
then  is a generalized (resp., linear) module-
is a generalized (resp., linear) module- left derivation and
left derivation and  is a (resp., linear) module-
is a (resp., linear) module- left derivation. It is also shown that if
left derivation. It is also shown that if  (resp.,
(resp.,  is dominated by
is dominated by  then
then  is a generalized (resp., linear) module-
is a generalized (resp., linear) module- derivation and
derivation and  is a (resp., linear) module-
is a (resp., linear) module- derivation.
derivation.
1. Introduction
The study of stability problems had been formulated by Ulam in [1] during a talk in 1940: under what condition does there exist a homomorphism near an approximate homomorphism? In the following year 1941, Hyers in [2] has answered affirmatively the question of Ulam for Banach spaces, which states that if  and
and  is a map with
is a map with  , a normed space,
, a normed space,  , a Banach space, such that
, a Banach space, such that

for all  in
in  , then there exists a unique additive mapping
, then there exists a unique additive mapping  such that
such that

for all  in
in  . In addition, if the mapping
. In addition, if the mapping  is continuous in
is continuous in  for each fixed
for each fixed  in
in  , then the mapping
, then the mapping  is real linear. This stability phenomenon is called the Hyers-Ulam stability of the additive functional equation
is real linear. This stability phenomenon is called the Hyers-Ulam stability of the additive functional equation  . A generalized version of the theorem of Hyers for approximately additive mappings was given by Aoki in [3] and for approximate linear mappings was presented by Rassias in [4] by considering the case when the left-hand side of (1.1) is controlled by a sum of powers of norms. The stability result concerning derivations between operator algebras was first obtained by Šemrl in [5], Badora in [6] gave a generalization of Bourgin's result [7]. He also discussed the Hyers-Ulam stability and the Bourgin-type superstability of derivations in [8].
. A generalized version of the theorem of Hyers for approximately additive mappings was given by Aoki in [3] and for approximate linear mappings was presented by Rassias in [4] by considering the case when the left-hand side of (1.1) is controlled by a sum of powers of norms. The stability result concerning derivations between operator algebras was first obtained by Šemrl in [5], Badora in [6] gave a generalization of Bourgin's result [7]. He also discussed the Hyers-Ulam stability and the Bourgin-type superstability of derivations in [8].
Singer and Wermer in [9] obtained a fundamental result which started investigation into the ranges of linear derivations on Banach algebras. The result, which is called the Singer-Wermer theorem, states that any continuous linear derivation on a commutative Banach algebra maps into the Jacobson radical. They also made a very insightful conjecture, namely, that the assumption of continuity is unnecessary. This was known as the Singer- Wermer conjecture and was proved in 1988 by Thomas in [10]. The Singer-Wermer conjecture implies that any linear derivation on a commutative semisimple Banach algebra is identically zero [11]. After then, Hatori and Wada in [12] proved that the zero operator is the only derivation on a commutative semisimple Banach algebra with the maximal ideal space without isolated points. Based on these facts and a private communication with Watanabe [13], Miura et al. proved the Hyers-Ulam-Rassias stability and Bourgin-type superstability of derivations on Banach algebras in [13]. Various stability results on derivations and left derivations can be found in [14–20]. More results on stability and superstability of homomorphisms, special functionals, and equations can be found in [21–30].
Recently, Kang and Chang in [31] discussed the superstability of generalized left derivations and generalized derivations. Indeed, these superstabilities are the so-called "Hyers-Ulam superstabilities." In the present paper, we will discuss the superstability of generalized module left derivations and generalized module derivations on a Banach module.
To give our results, let us give some notations. Let  be an algebra over the real or complex field
be an algebra over the real or complex field  and
and  an
an  -bimodule.
-bimodule.
Definition 1.1.
A mapping  is said to be module-
is said to be module- additive if
additive if

A module- additive mapping
additive mapping  is said to be a module-
is said to be a module- left derivation (resp., module-
left derivation (resp., module- derivation) if the functional equation
derivation) if the functional equation

respectively,

holds.
Definition 1.2.
A mapping  is said to be module-
is said to be module- additive if
additive if

A module- additive mapping
additive mapping  is called a generalized module-
is called a generalized module- left derivation (resp., generalized module-
left derivation (resp., generalized module- derivation) if there exists a module-
derivation) if there exists a module- left derivation (resp., module-
left derivation (resp., module- derivation)
derivation)  such that
such that

respectively,

In addition, if the mappings  and
and  are all linear, then the mapping
are all linear, then the mapping  is called a linear generalized module-
is called a linear generalized module- left derivation (resp., linear generalized module-
left derivation (resp., linear generalized module- derivation).
derivation).
Remark 1.3.
Let  and
and  be one of the following cases: (a) a unital algebra; (b) a Banach algebra with an approximate unit; (c) a
be one of the following cases: (a) a unital algebra; (b) a Banach algebra with an approximate unit; (c) a  -algebra. Then module-
-algebra. Then module- left derivations, module-
left derivations, module- derivations, generalized module-
derivations, generalized module- left derivations, and generalized module-
left derivations, and generalized module- derivations on
derivations on  become left derivations, derivations, generalized left derivations, and generalized derivations on
become left derivations, derivations, generalized left derivations, and generalized derivations on  discussed in [31].
discussed in [31].
2. Main Results
Theorem 2.1.
Let  be a Banach algebra,
be a Banach algebra,  a Banach
a Banach  -bimodule,
-bimodule,  and
and  integers greater than 1, and
integers greater than 1, and  satisfy the following conditions:
satisfy the following conditions:
(a)
(b)
(c)
Suppose that  and
and  are mappings such that
are mappings such that  ,
,  exists for all
exists for all  and
and

for all  and
and  where
where

Then  is a generalized module-
is a generalized module- left derivation and
left derivation and  is a module-
is a module- left derivation.
left derivation.
Proof.
By taking  , we see from (2.1) that
, we see from (2.1) that

for all  . Letting
. Letting  and replacing
and replacing  by
by  in (2.3) yield that
in (2.3) yield that

for all  . From [32, Theorem 1] (analogously as in [33, the proof of Theorem 1] or [34]), one can easily deduce that the limit
. From [32, Theorem 1] (analogously as in [33, the proof of Theorem 1] or [34]), one can easily deduce that the limit  exists for every
exists for every  ,
,  and
and

Next, we show that the mapping  is additive. To do this, let us replace
is additive. To do this, let us replace  by
by  in (2.3), respectively. Then
in (2.3), respectively. Then

for all  . If we let
. If we let  in the above inequality, then the condition (a) yields that
in the above inequality, then the condition (a) yields that

for all  . Since
. Since  , taking
, taking  and
and  , respectively, we see that
, respectively, we see that  and
and  for all
for all  . Now, for all
. Now, for all  , put
, put  . Then by (2.7), we get that
. Then by (2.7), we get that

This shows that  is additive.
is additive.
Now, we are going to prove that  is a generalized module-
is a generalized module- left derivation. Letting
left derivation. Letting  in (2.1) gives that
in (2.1) gives that

that is,

for all  and
and  . By replacing
. By replacing  with
with  in (2.10), respectively, we deduce that
in (2.10), respectively, we deduce that

for all  and
and  . Letting
. Letting  , the condition (b) yields that
, the condition (b) yields that

for all  and
and  . Since
. Since  is additive,
is additive,  is module-
is module- additive. Put
additive. Put  . Then by (2.10) we see from the condition (a) that
. Then by (2.10) we see from the condition (a) that

for all  and
and  . Hence
. Hence

for all  and
and  . It follows from (2.12) that
. It follows from (2.12) that  for all
for all  and
and  , and then
, and then  for all
for all  . Since
. Since  is additive,
is additive,  is module-
is module- additive. So, for all
additive. So, for all  and
and  by (2.12)
by (2.12)

This shows that  is a module-
is a module- left derivation on
left derivation on  and then
and then  is a generalized module-
is a generalized module- left derivation on
left derivation on  .
.
Lastly, we prove that  is a module-
is a module- left derivation on
left derivation on  . To do this, we compute from (2.10) that
. To do this, we compute from (2.10) that

for all  . By letting
. By letting  , we get from the condition (a) that
, we get from the condition (a) that

for all  . Now, (2.12) implies that
. Now, (2.12) implies that  for all
for all  and all
and all  . Hence,
. Hence,  is a module-
is a module- left derivation on
left derivation on  . This completes the proof.
. This completes the proof.
Remark 2.2.
It is easy to check that the functional  satisfies the conditions (a), (b), and (c) in Theorem 2.1, where
satisfies the conditions (a), (b), and (c) in Theorem 2.1, where  ,
,  . Especially, if
. Especially, if  has a unit and
has a unit and  are mappings with
are mappings with  such that
such that  for all
for all  , then
, then  is a generalized left derivation and
is a generalized left derivation and  is a left derivation.
is a left derivation.
Remark 2.3.
In Theorem 2.1, if the condition (2.1) is replaced with

for all  and
and  where
where

then  is a generalized module-
is a generalized module- derivation and
derivation and  is a module-
is a module- derivation. Especially, if
derivation. Especially, if  has a unit and
has a unit and  are mappings with
are mappings with  such that
such that  for all
for all  and some constants
and some constants  , then
, then  is a generalized derivation and
is a generalized derivation and  is a derivation.
is a derivation.
Lemma 2.4.
Let  be complex vector spaces. Then a mapping
be complex vector spaces. Then a mapping  is linear if and only if
is linear if and only if

for all  and all
and all  .
.
Proof.
It suffices to prove the sufficiency. Suppose that  for all
for all  and all
and all  . Then
. Then  is additive and
is additive and  for all
for all  and all
and all  Let
Let  be any nonzero complex number. Take a positive integer
be any nonzero complex number. Take a positive integer  such that
such that  . Take a real number
. Take a real number  such that
such that  . Put
. Put  . Then
. Then  and, therefore,
and, therefore,

for all  . This shows that
. This shows that  is linear. The proof is completed.
is linear. The proof is completed.
Theorem 2.5.
Let  be a Banach algebra,
be a Banach algebra,  a Banach
a Banach  -bimodule,
-bimodule,  and
and  integers greater than
integers greater than  , and
, and  satisfy the following conditions:
satisfy the following conditions:
(a)
(b)
(c) .
.
Suppose that  and
and  are mappings such that
are mappings such that  ,
,  exists for all
exists for all  and
and

for all  ,
,  and all
and all  , where
, where  stands for
stands for

Then  is a linear generalized module-
is a linear generalized module- left derivation and
left derivation and  is a linear module-
is a linear module- left derivation.
left derivation.
Proof.
Clearly, the inequality (2.1) is satisfied. Hence, Theorem 2.1 and its proof show that  is a generalized left derivation and
is a generalized left derivation and  is a left derivation on
is a left derivation on  with
with

for every  . Taking
. Taking  in (2.22) yields that
in (2.22) yields that

for all  and all
and all  . If we replace
. If we replace  and
and  with
with  and
and  in (2.25), respectively, then we see that
in (2.25), respectively, then we see that

as  for all
for all  and all
and all  . Hence,
. Hence,

for all  and all
and all  . Since
. Since  is additive, taking
is additive, taking  in (2.27) implies that
in (2.27) implies that

for all  and all
and all  . Lemma 2.4 yields that
. Lemma 2.4 yields that  is linear and so is
is linear and so is  . This completes the proof.
. This completes the proof.
Remark 2.6.
It is easy to check that the functional  satisfies the conditions (a), (b), and (c) in Theorem 2.5, where
satisfies the conditions (a), (b), and (c) in Theorem 2.5, where  ,
,  are constants. Especially, if
are constants. Especially, if  is a complex semiprime Banach algebra with unit and
is a complex semiprime Banach algebra with unit and  are mappings with
are mappings with  such that
such that

for all  . Then
. Then  is a linear generalized left derivation and
is a linear generalized left derivation and  is a linear derivation which maps
is a linear derivation which maps  into the intersection of the center
into the intersection of the center  and the Jacobson radical
and the Jacobson radical  of
of  .
.
Remark 2.7.
In Theorem 2.5, if the condition (2.22) is replaced with

for all  ,
,  and
and  where
where  stands for
stands for

then  is a linear generalized module-
is a linear generalized module- derivation on
derivation on  and
and  is a linear module-
is a linear module- derivation on
derivation on  . Especially, if
. Especially, if  is a unital commutative Banach algebra and
is a unital commutative Banach algebra and  are mappings with
are mappings with  such that
such that  for all
for all  , all
, all  and some constants
and some constants  , then
, then  is a linear generalized derivation and
is a linear generalized derivation and  is a linear derivation which maps
is a linear derivation which maps  into the Jacobson radical rad
into the Jacobson radical rad of
of  .
.
Remark 2.8.
The controlling function

consists of the "mixed sum-product of powers of norms," introduced by Rassias (in 2007) [28] and applied afterwards by Ravi et al. (2007-2008). Moreover, it is easy to check that the functional

satisfies theconditions (a), (b), and (c) in Theorems 2.1 and 2.5, where  and
and  are all constants.
are all constants.
References
Ulam SM: Problems in Modern Mathematics. John Wiley & Sons, New York, NY, USA; 1964:xvii+150.
Hyers DH: On the stability of the linear functional equation. Proceedings of the National Academy of Sciences 1941, 27: 222–224. 10.1073/pnas.27.4.222
Aoki T: On the stability of the linear transformation in Banach spaces. Journal of the Mathematical Society of Japan 1950, 2: 64–66. 10.2969/jmsj/00210064
Rassias TM: On the stability of the linear mapping in Banach spaces. Proceedings of the American Mathematical Society 1978,72(2):297–300. 10.1090/S0002-9939-1978-0507327-1
Šemrl P: The functional equation of multiplicative derivation is superstable on standard operator algebras. Integral Equations and Operator Theory 1994,18(1):118–122. 10.1007/BF01225216
Badora R: On approximate ring homomorphisms. Journal of Mathematical Analysis and Applications 2002,276(2):589–597. 10.1016/S0022-247X(02)00293-7
Bourgin DG: Approximately isometric and multiplicative transformations on continuous function rings. Duke Mathematical Journal 1949, 16: 385–397. 10.1215/S0012-7094-49-01639-7
Badora R: On approximate derivations. Mathematical Inequalities & Applications 2006,9(1):167–173.
Singer IM, Wermer J: Derivations on commutative normed algebras. Mathematische Annalen 1955, 129: 260–264. 10.1007/BF01362370
Thomas MP: The image of a derivation is contained in the radical. Annals of Mathematics 1988,128(3):435–460. 10.2307/1971432
Johnson BE: Continuity of derivations on commutative algebras. American Journal of Mathematics 1969, 91: 1–10. 10.2307/2373262
Hatori O, Wada J: Ring derivations on semi-simple commutative Banach algebras. Tokyo Journal of Mathematics 1992,15(1):223–229. 10.3836/tjm/1270130262
Miura T, Hirasawa G, Takahasi S-E: A perturbation of ring derivations on Banach algebras. Journal of Mathematical Analysis and Applications 2006,319(2):522–530. 10.1016/j.jmaa.2005.06.060
Amyari M, Baak C, Moslehian MS: Nearly ternary derivations. Taiwanese Journal of Mathematics 2007,11(5):1417–1424.
Moslehian MS: Ternary derivations, stability and physical aspects. Acta Applicandae Mathematicae 2008,100(2):187–199. 10.1007/s10440-007-9179-x
Moslehian MS: Hyers-Ulam-Rassias stability of generalized derivations. International Journal of Mathematics and Mathematical Sciences 2006, 2006:-8.
Park C-G: Homomorphisms between
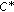 -algebras,
-algebras, 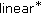 -derivations on a
-derivations on a 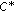 -algebra and the Cauchy-Rassias stability. Nonlinear Functional Analysis and Applications 2005,10(5):751–776.
-algebra and the Cauchy-Rassias stability. Nonlinear Functional Analysis and Applications 2005,10(5):751–776.Park C-G: Linear derivations on Banach algebras. Nonlinear Functional Analysis and Applications 2004,9(3):359–368.
Amyari M, Rahbarnia F, Sadeghi Gh: Some results on stability of extended derivations. Journal of Mathematical Analysis and Applications 2007,329(2):753–758. 10.1016/j.jmaa.2006.07.027
Brešar M, Vukman J: On left derivations and related mappings. Proceedings of the American Mathematical Society 1990,110(1):7–16.
Găvruţa P: A generalization of the Hyers-Ulam-Rassias stability of approximately additive mappings. Journal of Mathematical Analysis and Applications 1994,184(3):431–436. 10.1006/jmaa.1994.1211
Ulam SM: Problems in Modern Mathematics. John Wiley & Sons, New York, NY, USA; 1960:xiii+150.
Baker JA: The stability of the cosine equation. Proceedings of the American Mathematical Society 1980,80(3):411–416. 10.1090/S0002-9939-1980-0580995-3
Hyers DH, Rassias TM: Approximate homomorphisms. Aequationes Mathematicae 1992,44(2–3):125–153. 10.1007/BF01830975
Rassias TM, Tabo J (Eds): Stability of Mappings of Hyers-Ulam Type, Hadronic Press Collection of Original Articles. Hadronic Press, Palm Harbor, Fla, USA; 1994:vi+173.
Hyers DH, Isac G, Rassias TM: Stability of Functional Equations in Several Variables, Progress in Nonlinear Differential Equations and Their Applications, 34. Birkhäuser, Boston, Mass, USA; 1998:vi+313.
Isac G, Rassias TM: On the Hyers-Ulam stability of
 -additive mappings. Journal of Approximation Theory 1993,72(2):131–137. 10.1006/jath.1993.1010
-additive mappings. Journal of Approximation Theory 1993,72(2):131–137. 10.1006/jath.1993.1010Rassias JM, Rassias MJ: Refined Ulam stability for Euler-Lagrange type mappings in Hilbert spaces. International Journal of Applied Mathematics & Statistics 2007, 7: 126–132.
Rassias JM, Rassias MJ: The Ulam problem for 3-dimensional quadratic mappings. Tatra Mountains Mathematical Publications 2006, 34, part 2: 333–337.
Rassias JM, Rassias MJ: On the Hyers-Ulam stability of quadratic mappings. The Journal of the Indian Mathematical Society 2000,67(1–4):133–136.
Kang S-Y, Chang I-S: Approximation of generalized left derivations. Abstract and Applied Analysis 2008, -8.
Forti GL: Comments on the core of the direct method for proving Hyers-Ulam stability of functional equations. Journal of Mathematical Analysis and Applications 2004,295(1):127–133. 10.1016/j.jmaa.2004.03.011
Brzdęk J, Pietrzyk A: A note on stability of the general linear equation. Aequationes Mathematicae 2008,75(3):267–270. 10.1007/s00010-007-2894-6
Pietrzyk A: Stability of the Euler-Lagrange-Rassias functional equation. Demonstratio Mathematica 2006,39(3):523–530.
Acknowledgment
This subject is supported by the NNSFs of China (no: 10571113,10871224).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cao, HX., Lv, JR. & Rassias, J.M. Superstability for Generalized Module Left Derivations and Generalized Module Derivations on a Banach Module (I). J Inequal Appl 2009, 718020 (2009). https://doi.org/10.1155/2009/718020
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/718020
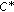 -algebras,
-algebras, 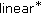 -derivations on a
-derivations on a 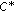 -algebra and the Cauchy-Rassias stability. Nonlinear Functional Analysis and Applications 2005,10(5):751–776.
-algebra and the Cauchy-Rassias stability. Nonlinear Functional Analysis and Applications 2005,10(5):751–776. -additive mappings. Journal of Approximation Theory 1993,72(2):131–137. 10.1006/jath.1993.1010
-additive mappings. Journal of Approximation Theory 1993,72(2):131–137. 10.1006/jath.1993.1010