- Research Article
- Open access
- Published:
A Generalized Wirtinger's Inequality with Applications to a Class of Ordinary Differential Equations
Journal of Inequalities and Applications volume 2009, Article number: 710475 (2009)
Abstract
We first prove a generalized Wirtinger's inequality. Then, applying the inequality, we study estimates for lower bounds of periods of periodic solutions for a class of delay differential equations  , and
, and  , where
, where  ,
,  , and
, and  and
and  ,
,  are two given constants. Under some suitable conditions on
are two given constants. Under some suitable conditions on  and
and  , lower bounds of periods of periodic solutions for the equations aforementioned are obtained.
, lower bounds of periods of periodic solutions for the equations aforementioned are obtained.
1. Introduction and Statement of Main Results
In the present paper, we are concerned with a generalized Wirtinger's inequality and estimates for lower bounds of periods of periodic solutions for the following autonomous delay differential equation:

and the following nonautonomous delay differential equation

where  ,
,  , and
, and  , and
, and  are two given constants.
are two given constants.
For the special case that  and
and  , various problems on the solutions of (1.1), such as the existence of periodic solutions, bifurcations of periodic solutions, and stability of solutions, have been studied by many authors since 1970s of the last century, and a lot of remarkable results have been achieved. We refer to [1–6] for reference.
, various problems on the solutions of (1.1), such as the existence of periodic solutions, bifurcations of periodic solutions, and stability of solutions, have been studied by many authors since 1970s of the last century, and a lot of remarkable results have been achieved. We refer to [1–6] for reference.
The delay equation (1.1) with more than one delay and  is also considered by a lot of researchers (see [7–13]). Most of the work contained in literature on (1.1) is the existence and multiplicity of periodic solutions. However, except the questions of the existence of periodic solutions with prescribed periods, little information was given on the periods of periodic solutions. Moreover, few work on the nonautonomous delay differential equation (1.2) has been done to the best of the author knowledge. Motivated by these cases, as a part of this paper, we study the estimates of periods of periodic solutions for the differential delay equation (1.1) and the nonautonomous equation (1.2). We first give a generalized Wirtinger's inequality. Then we turn to consider the problems on (1.1) and (1.2) by using the inequality.
is also considered by a lot of researchers (see [7–13]). Most of the work contained in literature on (1.1) is the existence and multiplicity of periodic solutions. However, except the questions of the existence of periodic solutions with prescribed periods, little information was given on the periods of periodic solutions. Moreover, few work on the nonautonomous delay differential equation (1.2) has been done to the best of the author knowledge. Motivated by these cases, as a part of this paper, we study the estimates of periods of periodic solutions for the differential delay equation (1.1) and the nonautonomous equation (1.2). We first give a generalized Wirtinger's inequality. Then we turn to consider the problems on (1.1) and (1.2) by using the inequality.
In order to state our main results, we make the following definitions.
Definition 1.1.
For a positive constant  ,
,  is called
is called  -Lipschitz continuous, if for all
-Lipschitz continuous, if for all  ,
,

where  denotes the norm in
denotes the norm in  .
.
Definition 1.2.
For a positive constant  ,
,  is called
is called  -Lipschitz continuous uniformly in
-Lipschitz continuous uniformly in  , if for all
, if for all  , and any
, and any  ,
,

Then our main results read as follows.
Theorem 1.3.
Let  be a nontrivial
be a nontrivial  -periodic solution of the autonomous delay differential equation (1.1) with the second derivative. Suppose that the function
-periodic solution of the autonomous delay differential equation (1.1) with the second derivative. Suppose that the function  is
is  -Lipschitz continuous. Then one has
-Lipschitz continuous. Then one has  .
.
Theorem 1.4.
Let  be a nontrivial
be a nontrivial  -periodic solution of the nonautonomous delay differential equation (1.2) with the second derivative. Suppose that the function
-periodic solution of the nonautonomous delay differential equation (1.2) with the second derivative. Suppose that the function  is
is  -periodic with respect to
-periodic with respect to  and
and  -Lipschitz continuous uniformly in
-Lipschitz continuous uniformly in  . If the following limit
. If the following limit

exists for all  and
and  and
and  is uniformly bounded, then one has
is uniformly bounded, then one has  .
.
2. Proof of the Main Results
We will apply Wirtinger's inequality to prove the two theorems. Firstly, let us recall some notation concerning the Sobolev space. It is well known that  is a Hilbert space consisting of the
is a Hilbert space consisting of the  -periodic functions
-periodic functions  on
on  which together with weak derivatives belong to
which together with weak derivatives belong to  . For all
. For all  , let
, let  and
and  denote the inner product and the norm in
denote the inner product and the norm in  , respectively, where
, respectively, where  is the inner product in
is the inner product in  . Then according to [14], we give Wirtinger's inequality and its proof.
. Then according to [14], we give Wirtinger's inequality and its proof.
Lemma 2.1.
If  and
and  , then
, then

Proof.
By the assumptions,  has the following Fourier expansion:
has the following Fourier expansion:

Then Parseval equality yields that

This completes the proof.
Now, we generalize Wirtinger's inequality to a more general form which includes (2.1) as a special case. We prove the following lemma.
Lemma 2.2.
Suppose that  and
and  with
with  . Then
. Then

Proof.
Since  , by Lemma 2.1, we have
, by Lemma 2.1, we have

that is,

Let  denote the average of
denote the average of  , that is,
, that is,  . This means that
. This means that  . Hence, Schwarz inequality, together with (2.6) and
. Hence, Schwarz inequality, together with (2.6) and  implies that
implies that

Then the proof is complete.
Corollary 2.3.
Under the conditions of Lemma 2.1, the inequality (2.4) implies Wirtinger's inequality (2.1).
Proof.
If  and
and  , then (2.1) follows (2.4) on taking
, then (2.1) follows (2.4) on taking  .
.
We call (2.4) a generalized Wirtinger's inequality. For other study of Wirtinger's inequality, one may see [15] and the references therein. Now, we are ready to prove our main results. We first give the proof of Theorem 1.3.
Proof of Theorem 1.3.
From (1.1) and Definition 1.1, for all  , one has
, one has

Hence, since  has the second derivative,
has the second derivative,

Noting that  is also
is also  -periodic,
-periodic,  =
=  , for
, for  . Hence, by Hölder inequality, one has
. Hence, by Hölder inequality, one has

that is,

From (2.1) and  , we have
, we have

Combining (2.11) and (2.12), one has 
Now, we prove Theorem 1.4.
Proof.
From (1.2), Definition 1.2 and the assumptions of Theorem 1.4, for all  , one has
, one has

Since  is nonnegative and uniformly bounded (for all
is nonnegative and uniformly bounded (for all  and
and  ), there is
), there is  such that
such that  . Together with the fact that
. Together with the fact that  has the second derivative, our estimates imply that
has the second derivative, our estimates imply that

As in the proof of Theorem 1.3, we get

that is,

Thus, (2.1) together with (2.16) yields that

By an argument of Viete theorem with respect to the quadratic function  , we have that
, we have that

Remark 2.4.
Roughly speaking, the period  can reach the lower bound
can reach the lower bound  . Let us take an example for (1.1). Take
. Let us take an example for (1.1). Take  and
and  . For each
. For each  , we define a function
, we define a function  by
by

Then one can check easily that  is
is  -Lipschitz continuous with
-Lipschitz continuous with  . Let
. Let  . One has
. One has

This means that  is a periodic solution of (1.2) with period
is a periodic solution of (1.2) with period  .
.
References
Han M: Bifurcations of periodic solutions of delay differential equations. Journal of Differential Equations 2003,189(2):396–411. 10.1016/S0022-0396(02)00106-7
Nussbaum RD: A Hopf global bifurcation theorem for retarded functional differential equations. Transactions of the American Mathematical Society 1978, 238: 139–164.
Kaplan JL, Yorke JA: Ordinary differential equations which yield periodic solutions of differential delay equations. Journal of Mathematical Analysis and Applications 1974,48(2):317–324. 10.1016/0022-247X(74)90162-0
Nussbaum RD: Uniqueness and nonuniqueness for periodic solutions of
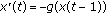 . Journal of Differential Equations 1979,34(1):25–54. 10.1016/0022-0396(79)90016-0
. Journal of Differential Equations 1979,34(1):25–54. 10.1016/0022-0396(79)90016-0Dormayer P: The stability of special symmetric solutions of
 with small amplitudes. Nonlinear Analysis: Theory, Methods & Applications 1990,14(8):701–715. 10.1016/0362-546X(90)90045-I
with small amplitudes. Nonlinear Analysis: Theory, Methods & Applications 1990,14(8):701–715. 10.1016/0362-546X(90)90045-IFurumochi T: Existence of periodic solutions of one-dimensional differential-delay equations. Tohoku Mathematical Journal 1978,30(1):13–35. 10.2748/tmj/1178230094
Chapin S: Periodic solutions of differential-delay equations with more than one delay. The Rocky Mountain Journal of Mathematics 1987,17(3):555–572. 10.1216/RMJ-1987-17-3-555
Li J, He X-Z, Liu Z: Hamiltonian symmetric groups and multiple periodic solutions of differential delay equations. Nonlinear Analysis: Theory, Methods & Applications 1999,35(4):457–474. 10.1016/S0362-546X(97)00623-8
Li J, He X-Z: Multiple periodic solutions of differential delay equations created by asymptotically linear Hamiltonian systems. Nonlinear Analysis: Theory, Methods & Applications 1998,31(1–2):45–54. 10.1016/S0362-546X(96)00058-2
Llibre J, Tarţa A-A: Periodic solutions of delay equations with three delays via bi-Hamiltonian systems. Nonlinear Analysis: Theory, Methods & Applications 2006,64(11):2433–2441. 10.1016/j.na.2005.08.023
Jekel S, Johnston C: A Hamiltonian with periodic orbits having several delays. Journal of Differential Equations 2006,222(2):425–438. 10.1016/j.jde.2005.08.013
Fei G: Multiple periodic solutions of differential delay equations via Hamiltonian systems—I. Nonlinear Analysis: Theory, Methods & Applications 2006,65(1):25–39. 10.1016/j.na.2005.06.011
Fei G: Multiple periodic solutions of differential delay equations via Hamiltonian systems—II. Nonlinear Analysis: Theory, Methods & Applications 2006,65(1):40–58. 10.1016/j.na.2005.06.012
Mawhin J, Willem M: Critical Point Theory and Hamiltonian Systems, Applied Mathematical Sciences. Volume 74. Springer, New York, NY, USA; 1989:xiv+277.
Milovanović GV, Milovanović IŽ: Discrete inequalities of Wirtinger's type for higher differences. Journal of Inequalities and Applications 1997,1(4):301–310. 10.1155/S1025583497000209
Acknowledgments
The authors would like to thank the referee for careful reading of the paper and many valuable suggestions. Supported by the specialized Research Fund for the Doctoral Program of Higher Education for New Teachers, the National Natural Science Foundation of China (10826035) and the Science Research Foundation of Nanjing University of Information Science and Technology (20070049).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cheng, R., Zhang, D. A Generalized Wirtinger's Inequality with Applications to a Class of Ordinary Differential Equations. J Inequal Appl 2009, 710475 (2009). https://doi.org/10.1155/2009/710475
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/710475
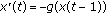 . Journal of Differential Equations 1979,34(1):25–54. 10.1016/0022-0396(79)90016-0
. Journal of Differential Equations 1979,34(1):25–54. 10.1016/0022-0396(79)90016-0 with small amplitudes. Nonlinear Analysis: Theory, Methods & Applications 1990,14(8):701–715. 10.1016/0362-546X(90)90045-I
with small amplitudes. Nonlinear Analysis: Theory, Methods & Applications 1990,14(8):701–715. 10.1016/0362-546X(90)90045-I