- Research Article
- Open access
- Published:
New Trace Bounds for the Product of Two Matrices and Their Applications in the Algebraic Riccati Equation
Journal of Inequalities and Applications volume 2009, Article number: 620758 (2009)
Abstract
By using singular value decomposition and majorization inequalities, we propose new inequalities for the trace of the product of two arbitrary real square matrices. These bounds improve and extend the recent results. Further, we give their application in the algebraic Riccati equation. Finally, numerical examples have illustrated that our results are effective and superior.
1. Introduction
In the analysis and design of controllers and filters for linear dynamical systems, the Riccati equation is of great importance in both theory and practice (see [1–5]). Consider the following linear system (see [4]):

with the cost

Moreover, the optimal control rate  and the optimal cost
and the optimal cost  of (1.1) and (1.2) are
of (1.1) and (1.2) are

where  is the initial state of the systems (1.1) and (1.2),
is the initial state of the systems (1.1) and (1.2),  is the positive definite solution of the following algebraic Riccati equation (ARE):
is the positive definite solution of the following algebraic Riccati equation (ARE):

with  and
and  are symmetric positive definite matrices. To guarantee the existence of the positive definite solution to (1.4), we shall make the following assumptions: the pair (
are symmetric positive definite matrices. To guarantee the existence of the positive definite solution to (1.4), we shall make the following assumptions: the pair ( ) is stabilizable, and the pair (
) is stabilizable, and the pair ( ) is observable.
) is observable.
In practice, it is hard to solve the (ARE), and there is no general method unless the system matrices are special and there are some methods and algorithms to solve (1.4), however, the solution can be time-consuming and computationally difficult, particularly as the dimensions of the system matrices increase. Thus, a number of works have been presented by researchers to evaluate the bounds and trace bounds for the solution of the (ARE) [6–12]. In addition, from [2, 6], we know that an interpretation of  is that
is that  is the average value of the optimal cost
is the average value of the optimal cost  as
as  varies over the surface of a unit sphere. Therefore, consider its applications, it is important to discuss trace bounds for the product of two matrices. Most available results are based on the assumption that at least one matrix is symmetric [7, 8, 11, 12]. However, it is important and difficult to get an estimate of the trace bounds when any matrix in the product is nonsymmetric in theory and practice. There are some results in [13–15].
varies over the surface of a unit sphere. Therefore, consider its applications, it is important to discuss trace bounds for the product of two matrices. Most available results are based on the assumption that at least one matrix is symmetric [7, 8, 11, 12]. However, it is important and difficult to get an estimate of the trace bounds when any matrix in the product is nonsymmetric in theory and practice. There are some results in [13–15].
In this paper, we propose new trace bounds for the product of two general matrices. The new trace bounds improve the recent results. Then, for their application in the algebraic Riccati equation, we get some upper and lower bounds.
In the following, let  denote the set of
denote the set of  real matrices. Let
real matrices. Let  be a real
be a real  -element array which is reordered, and its elements are arranged in nonincreasing order. That is,
-element array which is reordered, and its elements are arranged in nonincreasing order. That is,  . Let
. Let  . For
. For  , let
, let  ,
,  ,
,  denote the diagonal elements, the eigenvalues, the singular values of
denote the diagonal elements, the eigenvalues, the singular values of  , respectively, Let
, respectively, Let  denote the trace, the transpose of
denote the trace, the transpose of  , respectively. We define
, respectively. We define  ,
,  The notation
The notation  (
( ) is used to denote that
) is used to denote that  is a symmetric positive definite (semidefinite) matrix.
is a symmetric positive definite (semidefinite) matrix.
Let  be two real
be two real  -element arrays. If they satisfy
-element arrays. If they satisfy

then it is said that  is controlled weakly by
is controlled weakly by  , which is signed by
, which is signed by  .
.
If  and
and

then it is said that  is controlled by
is controlled by  , which is signed by
, which is signed by  .
.
Therefore, considering the application of the trace bounds, many scholars pay much attention to estimate the trace bounds for the product of two matrices.
Marshall and Olkin in [16] have showed that for any  then
then

Xing et al. in [13] have observed another result. Let  be arbitrary matrices with the following singular value decomposition:
be arbitrary matrices with the following singular value decomposition:

where  are orthogonal. Then
are orthogonal. Then

where  is orthogonal.
is orthogonal.
Liu and He in [14] have obtained the following: let  be arbitrary matrices with the following singular value decomposition:
be arbitrary matrices with the following singular value decomposition:

where  are orthogonal. Then
are orthogonal. Then

-
F.
Zhang and Q. Zhang in [15] have obtained the following: let
 be arbitrary matrices with the following singular value decomposition:
be arbitrary matrices with the following singular value decomposition: 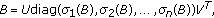 (1.12)
(1.12)
where  are orthogonal. Then
are orthogonal. Then

where  is orthogonal. They show that (1.13) has improved (1.9).
is orthogonal. They show that (1.13) has improved (1.9).
2. Main Results
The following lemmas are used to prove the main results.
Lemma 2.1 (see [16, page 92, H.2.c] ).
If  and
and  , then for any real array
, then for any real array  ,
,

Lemma 2.2 (see [16, page 95, H.3.b] ).
If  and
and  , then for any real array
, then for any real array  ,
,

Remark 2.3.
Note that if  , then for
, then for  ,
,  . Thus from Lemma 2.2, we have
. Thus from Lemma 2.2, we have

Lemma 2.4 (see [16, page 218, B.1] ).
Let  , then
, then

Lemma 2.5 (see [16, page 240, F.4.a] ).
Let  , then
, then

Lemma 2.6 (see [17] ).
Let  . Then
. Then

where

Note that if  or
or  , obviously, (2.6) holds. If
, obviously, (2.6) holds. If  , choose
, choose  , then (2.6) also holds.
, then (2.6) also holds.
Remark 2.7.
If  , then we obtain Cauchy-Schwartz inequality
, then we obtain Cauchy-Schwartz inequality

where

Remark 2.8.
Note that

Let  in (2.6), then we obtain
in (2.6), then we obtain

Lemma 2.9.
If  ,
,  , then
, then

Proof.
-
(1)
Note that
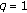 , or
, or  ,
,  (2.13)
(2.13)
-
(2)
If
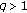 ,
, 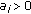 , for
, for 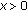 , choose
, choose 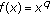 , then
, then 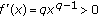 and
and 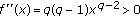 . Thus,
. Thus, 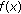 is a convex function. As
is a convex function. As 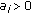 and
and  , from the property of the convex function, we have
, from the property of the convex function, we have  (2.14)
(2.14)
-
(3)
If
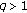 , without loss of generality, we may assume
, without loss of generality, we may assume 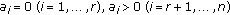 . Then from (2), we have
. Then from (2), we have 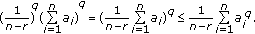 (2.15)
(2.15)
Since  , thus
, thus

This completes the proof.
Theorem 2.10.
Let  be arbitrary matrices with the following singular value decomposition:
be arbitrary matrices with the following singular value decomposition:

where  are orthogonal. Then
are orthogonal. Then

Proof.
By the matrix theory we have

Since  , without loss of generality, we may assume
, without loss of generality, we may assume  . Next, we will prove the left-hand side of (2.18):
. Next, we will prove the left-hand side of (2.18):

If

we obtain the conclusion. Now assume that there exists  such that
such that  then
then

We use  to denote the vector of
to denote the vector of  after changing
after changing  and
and  , then
, then

After limited steps, we obtain the the left-hand side of (2.18). For the right-hand side of (2.18),

If

we obtain the conclusion. Now assume that there exists  such that
such that  then
then

We use  to denote the vector of
to denote the vector of  after changing
after changing  and
and  , then
, then

After limited steps, we obtain the right-hand side of (2.18). Therefore,

This completes the proof.
Since  applying (2.18) with
applying (2.18) with  in lieu of
in lieu of  we immediately have the following corollary.
we immediately have the following corollary.
Corollary 2.11.
Let  be arbitrary matrices with the following singular value decomposition:
be arbitrary matrices with the following singular value decomposition:

where  are orthogonal. Then
are orthogonal. Then

Now using (2.18) and (2.30), one finally has the following theorem.
Theorem 2.12.
Let  be arbitrary matrices with the following singular value decompositions, respectively:
be arbitrary matrices with the following singular value decompositions, respectively:

where  are orthogonal. Then
are orthogonal. Then

Remark 2.13.
We point out that (2.18) improves (1.11). In fact, it is obvious that

This implies that (2.18) improves (1.11).
Remark 2.14.
We point out that (2.18) improves (1.13). Since for  ,
,  and
and  , from Lemmas 2.1 and 2.4, then (2.18) implies
, from Lemmas 2.1 and 2.4, then (2.18) implies

In fact, for  , we have
, we have

Then (2.34) can be rewritten as

This implies that (2.18) improves (1.13).
Remark 2.15.
We point out that (1.13) improves (1.7). In fact, from Lemma 2.5, we have

Since  is orthogonal,
is orthogonal,  . Then (2.37) is rewritten as follows:
. Then (2.37) is rewritten as follows:  By using
By using  and Lemma 2.2, we obtain
and Lemma 2.2, we obtain

Note that  , from Lemma 2.2 and (2.38), we have
, from Lemma 2.2 and (2.38), we have

Thus, we obtain

Both (2.38) and (2.40) show that (1.13) is tighter than (1.7).
3. Applications of the Results
Wang et al. in [6] have obtained the following: let  be the positive semidefinite solution of the ARE (1.4). Then the trace of matrix
be the positive semidefinite solution of the ARE (1.4). Then the trace of matrix  has the lower and upper bounds given by
has the lower and upper bounds given by

In this section, we obtain the application in the algebraic Riccati equation of our results including (3.1). Some of our results and (3.1) cannot contain each other.
Theorem 3.1.
If  and
and  is the positive semidefinite solution of the ARE (1.4), then
is the positive semidefinite solution of the ARE (1.4), then
-
(1)
the trace of matrix
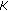 has the lower and upper bounds given by
has the lower and upper bounds given by 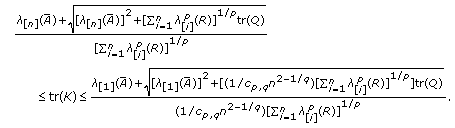 (3.2)
(3.2)
-
(2)
If
 , then the trace of matrix
, then the trace of matrix 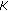 has the lower and upper bounds given by
has the lower and upper bounds given by 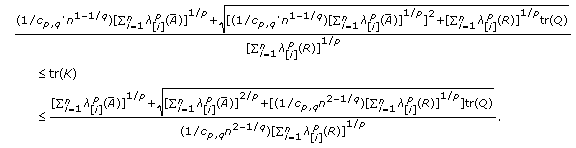 (3.3)
(3.3)
-
(3)
If
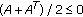 , then the trace of matrix
, then the trace of matrix  has the lower and upper bounds given by
has the lower and upper bounds given by 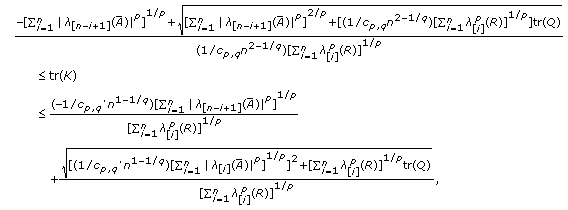 (3.4)
(3.4)
where

Proof.
-
(1)
Take the trace in both sides of the matrix ARE (1.4) to get
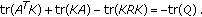 (3.6)
(3.6)
Since  is symmetric positive definite matrix,
is symmetric positive definite matrix,  ,
,  and from Lemma 2.9, we have
and from Lemma 2.9, we have


By the Cauchy-Schwartz inequality (2.8), it can be shown that

Note that


,  then by (2.34), use (2.6), considering (3.7) and (3.9), we have
then by (2.34), use (2.6), considering (3.7) and (3.9), we have

From (2.34), note that  and
and  then we obtain
then we obtain

It is easy to see that

Combine (3.11) and (3.13), we obtain

Solving (3.14) for  yields the right-hand side of the inequality (3.2). Similarly, we can obtain the left-hand side of the inequality (3.2).
yields the right-hand side of the inequality (3.2). Similarly, we can obtain the left-hand side of the inequality (3.2).
-
(2)
Note that when
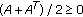 ,
, 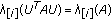 and
and  by (2.34), (2.6) and (3.7), we have
by (2.34), (2.6) and (3.7), we have  (3.15)
(3.15)
Thus,

From (3.11) and (3.16), with similar argument to (1), we can obtain (3.3) easily.
-
(3)
Note that when
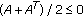 , by (3.3), we obtain (3.4) immediately. This completes the proof.
, by (3.3), we obtain (3.4) immediately. This completes the proof.
Remark 3.2.
From Remark 2.7 and Theorem 3.1, let  in (3.2), then we obtain
in (3.2), then we obtain

where 
Remark 3.3.
From Remark 2.7 and Theorem 3.1, let  in (3.2), then we obtain (3.1) immediately.
in (3.2), then we obtain (3.1) immediately.
4. Numerical Examples
In this section, firstly, we will give two examples to illustrate that our new trace bounds are better than the recent results. Then, to illustrate the application in the algebraic Riccati equation of our results will have different superiority if we choose different  and
and  , we will give two examples when
, we will give two examples when  and
and  .
.
Example 4.1 (see [13] ).
Now let

Neither  nor
nor  is symmetric. In this case, the results of [6–12] are not valid.
is symmetric. In this case, the results of [6–12] are not valid.
Using (1.9) we obtain

Using (1.11) yields

By (2.18), we obtain

where both lower and upper bounds are better than those of (4.2) and (4.3).
Example 4.2.
Let

Neither  nor
nor  is symmetric. In this case, the results of [6–12] are not valid.
is symmetric. In this case, the results of [6–12] are not valid.
Using (1.7) yields

From (1.9) we have

Using (1.11) yields

By (1.13), we obtain

The bound in (2.18) yields

Obviously, (4.10) is tighter than (4.6), (4.7), (4.8) and (4.9).
Example 4.3.
Consider the systems (1.1), (1.2) with

Moreover, the corresponding ARE (1.4) with  ,
,  is stabilizable and
is stabilizable and  is observable.
is observable.
Using (3.17) yields

Using (3.1) we obtain

where both lower and upper bounds are better than those of (4.12).
Example 4.4.
Consider the systems (1.1), (1.2) with

Moreover, the corresponding ARE (1.4) with  ,
,  is stabilizable and
is stabilizable and  is observable.
is observable.
Using (3.1) we obtain

Using (3.17) yields

where both lower and upper bounds are better than those of (4.15).
5. Conclusion
In this paper, we have proposed lower and upper bounds for the trace of the product of two arbitrary real matrices. We have showed that our bounds for the trace are the tightest among the parallel trace bounds in nonsymmetric case. Then, we have obtained the application in the algebraic Riccati equation of our results. Finally, numerical examples have illustrated that our bounds are better than the recent results.
References
Kwakernaak K, Sivan R: Linear Optimal Control Systems. John Wiley & Sons, New York, NY, USA; 1972.
Kleinman DL, Athans M: The design of suboptimal linear time-varying systems. IEEE Transactions on Automatic Control 1968,13(2):150–159. 10.1109/TAC.1968.1098852
Davies R, Shi P, Wiltshire R: New upper solution bounds for perturbed continuous algebraic Riccati equations applied to automatic control. Chaos, Solitons & Fractals 2007,32(2):487–495. 10.1016/j.chaos.2006.06.096
Ni M-L: Existence condition on solutions to the algebraic Riccati equation. Acta Automatica Sinica 2008,34(1):85–87.
Ogata K: Modern Control Engineering. 3rd edition. Prentice-Hall, Upper Saddle River, NJ, USA; 1997.
Wang S-D, Kuo T-S, Hsu C-F: Trace bounds on the solution of the algebraic matrix Riccati and Lyapunov equation. IEEE Transactions on Automatic Control 1986,31(7):654–656. 10.1109/TAC.1986.1104370
Lasserre JB: Tight bounds for the trace of a matrix product. IEEE Transactions on Automatic Control 1997,42(4):578–581. 10.1109/9.566673
Fang Y, Loparo KA, Feng X: Inequalities for the trace of matrix product. IEEE Transactions on Automatic Control 1994,39(12):2489–2490. 10.1109/9.362841
Saniuk J, Rhodes I: A matrix inequality associated with bounds on solutions of algebraic Riccati and Lyapunov equations. IEEE Transactions on Automatic Control 1987,32(8):739–740. 10.1109/TAC.1987.1104700
Mori T: Comments on "A matrix inequality associated with bounds on solutions of algebraic Riccati and Lyapunov equation". IEEE Transactions on Automatic Control 1988,33(11):1088–1091. 10.1109/9.14428
Lasserre JB: A trace inequality for matrix product. IEEE Transactions on Automatic Control 1995,40(8):1500–1501. 10.1109/9.402252
Park P: On the trace bound of a matrix product. IEEE Transactions on Automatic Control 1996,41(12):1799–1802. 10.1109/9.545717
Xing W, Zhang Q, Wang Q: A trace bound for a general square matrix product. IEEE Transactions on Automatic Control 2000,45(8):1563–1565. 10.1109/9.871773
Liu J, He L: A new trace bound for a general square matrix product. IEEE Transactions on Automatic Control 2007,52(2):349–352.
Zhang F, Zhang Q: Eigenvalue inequalities for matrix product. IEEE Transactions on Automatic Control 2006,51(9):1506–1509. 10.1109/TAC.2006.880787
Marshall AW, Olkin I: Inequalities: Theory of Majorization and Its Applications, Mathematics in Science and Engineering. Volume 143. Academic Press, New York, NY, USA; 1979:xx+569.
Wang C-L: On development of inverses of the Cauchy and Hölder inequalities. SIAM Review 1979,21(4):550–557. 10.1137/1021096
Acknowledgments
The author thanks the referee for the very helpful comments and suggestions. The work was supported in part by National Natural Science Foundation of China (10671164), Science and Research Fund of Hunan Provincial Education Department (06A070).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liu, J., Zhang, J. New Trace Bounds for the Product of Two Matrices and Their Applications in the Algebraic Riccati Equation. J Inequal Appl 2009, 620758 (2009). https://doi.org/10.1155/2009/620758
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/620758
 be arbitrary matrices with the following singular value decomposition:
be arbitrary matrices with the following singular value decomposition: 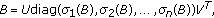
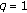 , or
, or  ,
, 
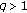 ,
, 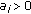 , for
, for 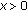 , choose
, choose 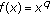 , then
, then 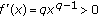 and
and 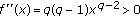 . Thus,
. Thus, 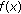 is a convex function. As
is a convex function. As 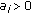 and
and  , from the property of the convex function, we have
, from the property of the convex function, we have 
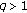 , without loss of generality, we may assume
, without loss of generality, we may assume 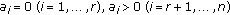 . Then from (2), we have
. Then from (2), we have 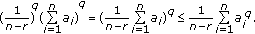
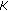 has the lower and upper bounds given by
has the lower and upper bounds given by 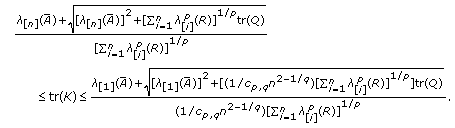
 , then the trace of matrix
, then the trace of matrix 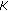 has the lower and upper bounds given by
has the lower and upper bounds given by 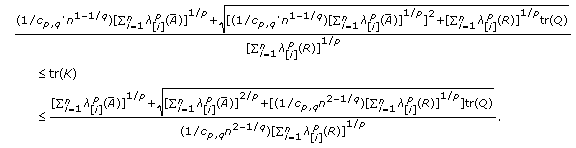
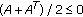 , then the trace of matrix
, then the trace of matrix  has the lower and upper bounds given by
has the lower and upper bounds given by 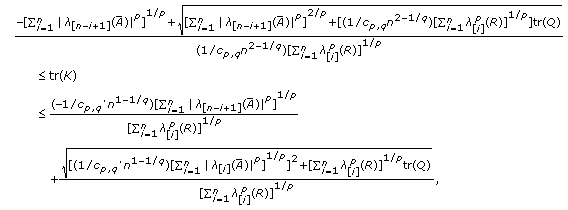
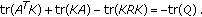
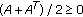 ,
, 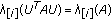 and
and  by (2.34), (2.6) and (3.7), we have
by (2.34), (2.6) and (3.7), we have 
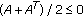 , by (3.3), we obtain (3.4) immediately. This completes the proof.
, by (3.3), we obtain (3.4) immediately. This completes the proof.