- Research Article
- Open access
- Published:
An Improved Hardy-Rellich Inequality with Optimal Constant
Journal of Inequalities and Applications volume 2009, Article number: 610530 (2009)
Abstract
We show that a Hardy-Rellich inequality with optimal constants on a bounded domain can be refined by adding remainder terms. The procedure is based on decomposition into spherical harmonics.
1. Introduction
Hardy inequality in  reads, for all
reads, for all  and
and  ,
,

and  is the best constant in (1.1) and is never achieved. A similar inequality with the same best constant holds if
is the best constant in (1.1) and is never achieved. A similar inequality with the same best constant holds if  is replaced by an arbitrary domain
is replaced by an arbitrary domain  and
and  contains the origin. Moreover, Brezis and Vázquez [1] have improved it by establishing that for
contains the origin. Moreover, Brezis and Vázquez [1] have improved it by establishing that for  ,
,

where  and
and  denote the volume of the unit ball
denote the volume of the unit ball  and
and  , respectively, and
, respectively, and  is the first eigenvalue of the Dirichlet Laplacian of the unit disc in
is the first eigenvalue of the Dirichlet Laplacian of the unit disc in  . In case
. In case  is a ball centered at zero, the constant
is a ball centered at zero, the constant  in (1.2) is sharp.
in (1.2) is sharp.
Similar improved inequalities have been recently proved if instead of (1.1) one considers the corresponding  Hardy inequalities. In all these cases a correction term is added on the right-hand side (see, e.g., [2–4]).
Hardy inequalities. In all these cases a correction term is added on the right-hand side (see, e.g., [2–4]).
On the other hand, the classical Rellich inequality states that, for  ,
,

and  is the best constant in (1.3) and is never achieved (see [5]). And, more recently, Tertikas and Zographopoulos [6] obtained a stronger version of Rellich's inequality. That is, for all
is the best constant in (1.3) and is never achieved (see [5]). And, more recently, Tertikas and Zographopoulos [6] obtained a stronger version of Rellich's inequality. That is, for all  ,
,

Both inequalities are valid when  is replaced by a bounded domain
is replaced by a bounded domain  containing the origin and the corresponding constants are known to be optimal. Recently, Gazzola et al. [4] have improved (1.3) by establishing that for
containing the origin and the corresponding constants are known to be optimal. Recently, Gazzola et al. [4] have improved (1.3) by establishing that for  and
and  ,
,

where

and  is the unit ball in
is the unit ball in  . Our main concern in this note is to improve (1.4). In fact we have the following theorem.
. Our main concern in this note is to improve (1.4). In fact we have the following theorem.
Theorem 1.1.
There holds, for  and
and  ,
,

Inequality (1.7) is optimal in case  is a ball centered at zero.
is a ball centered at zero.
Combining Theorem 1.1 with (1.2), we have the following.
Corollary 1.2.
There holds, for  and
and  ,
,

Next we consider analogous inequality (1.5). The main result is the following theorem.
Theorem 1.3.
Let  and let
and let  be such that
be such that  . Then for every
. Then for every  one has
one has

Remark 1.4.
Since

inequality (1.5) is implied by (1.9) in case of  .
.
2. The Proofs
To prove the main results, we first need the following preliminary result.
Lemma 2.1.
Let  and
and  . Set
. Set  . If
. If  is a radial function, that is,
is a radial function, that is,  , then
, then

Proof.
Observe that if  , then
, then

Therefore, we have

Though integration by parts, when  ,
,

and hence

By Lemma 2.1 and inequality (1.2), we have, when restricted to radial functions,

Our next step is to prove the following. If  is not a radial function, inequality (2.6) also holds.
is not a radial function, inequality (2.6) also holds.
Let  . If we extend
. If we extend  as zero outside
as zero outside  , we may consider
, we may consider  . Decomposing
. Decomposing  into spherical harmonics we get
into spherical harmonics we get

where  are the orthonormal eigenfunctions of the Laplace-Beltrami operator with responding eigenvalues
are the orthonormal eigenfunctions of the Laplace-Beltrami operator with responding eigenvalues

The functions  belong to
belong to  , satisfying
, satisfying  and
and  as
as  . In particular,
. In particular,  and
and  , for any
, for any  . Then, for any
. Then, for any  , we have
, we have

So

In addition,

Using equality (2.10), we have that (see, e.g., [6, page 452])

Therefore, we have that, by (2.12),

Lemma 2.2.
There holds, for  and
and  ,
,

Proof.
Set  . Then
. Then  satisfies
satisfies  and
and  as
as  . Moreover, since
. Moreover, since  belong to
belong to  , we have that
, we have that

Here we use the fact when  and
and  ,
,

Using inequalities (1.2) and (2.15), we have that, for  and
and  ,
,

An immediate consequence of the inequalities (2.13) and Lemma 2.2 is the following result. For  ,
,

Using inequalities (2.18) and Lemma 2.1, we have that, since  , for
, for  ,
,

Inequality (2.19) implies that, if  is not a radial function, then
is not a radial function, then

Proof of Theorem 1.1.
Using inequality (2.6) and (2.20), we have that, for  and
and  ,
,

In case  is a ball centered at zero, a simple scaling allows to consider the case
is a ball centered at zero, a simple scaling allows to consider the case  . Set
. Set

Using Lemma 2.1 and inequality (1.2), we have that  . On the other hand, we have, by inequality (2.21),
. On the other hand, we have, by inequality (2.21),  . Thus
. Thus  . The proof is complete.
. The proof is complete.
Proof of Theorem 1.3.
A scaling argument shows that we may assume  and
and  .
.
Step 1.
Assume  is radial,
is radial,  and
and  , then (see [6, Lemma
, then (see [6, Lemma  ])
])

and (see [6, (6.4)])

Therefore

Since  is radial,
is radial,

where  denote the surface area of the unit sphere in
denote the surface area of the unit sphere in  ,
,  is the unit ball in
is the unit ball in  , and
, and

is the radial Laplacian in  .
.
Therefore, for  ,
,

Step 2.
For  , set
, set

We get, by (2.18),

In getting the last equality, we used Lemma 2.1.
Using inequality (1.9) for radial functions from step 1,

one obtains, by (2.11),

which demonstrates inequality (1.9).
References
Brezis H, Vázquez JL: Blow-up solutions of some nonlinear elliptic problems. Revista Matemática de la Universidad Complutense de Madrid 1997,10(2):443–469.
Adimurthi , Chaudhuri N, Ramaswamy M: An improved Hardy-Sobolev inequality and its application. Proceedings of the American Mathematical Society 2002,130(2):489–505. 10.1090/S0002-9939-01-06132-9
Filippas S, Tertikas A: Optimizing improved Hardy inequalities. Journal of Functional Analysis 2002,192(1):186–233. 10.1006/jfan.2001.3900
Gazzola F, Grunau H-C, Mitidieri E: Hardy inequalities with optimal constants and remainder terms. Transactions of the American Mathematical Society 2004,356(6):2149–2168. 10.1090/S0002-9947-03-03395-6
Davies EB, Hinz AM: Explicit constants for Rellich inequalities in
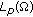 . Mathematische Zeitschrift 1998,227(3):511–523. 10.1007/PL00004389
. Mathematische Zeitschrift 1998,227(3):511–523. 10.1007/PL00004389Tertikas A, Zographopoulos NB: Best constants in the Hardy-Rellich inequalities and related improvements. Advances in Mathematics 2007,209(2):407–459. 10.1016/j.aim.2006.05.011
Acknowledgment
This work was supported by National Science Foundation of China under Grant no. 10571044.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xiao, YX., Yang, QH. An Improved Hardy-Rellich Inequality with Optimal Constant. J Inequal Appl 2009, 610530 (2009). https://doi.org/10.1155/2009/610530
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/610530
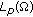 . Mathematische Zeitschrift 1998,227(3):511–523. 10.1007/PL00004389
. Mathematische Zeitschrift 1998,227(3):511–523. 10.1007/PL00004389