- Research Article
- Open access
- Published:
On a Hilbert-Type Operator with a Class of Homogeneous Kernels
Journal of Inequalities and Applications volume 2009, Article number: 572176 (2009)
Abstract
By using the way of weight coefficient and the theory of operators, we define a Hilbert-type operator with a class of homogeneous kernels and obtain its norm. As applications, an extended basic theorem on Hilbert-type inequalities with the decreasing homogeneous kernels of  -degree is established, and some particular cases are considered.
-degree is established, and some particular cases are considered.
1. Introduction
In 1908, Weyl published the well-known Hilbert's inequality as the following. If  are real sequences,
are real sequences,  and
and  then [1]
then [1]

where the constant factor  is the best possible. In 1925, Hardy gave an extension of (1.1) by introducing one pair of conjugate exponents
is the best possible. In 1925, Hardy gave an extension of (1.1) by introducing one pair of conjugate exponents  as [2]. If
as [2]. If  ,
,  , and
, and  then
then

where the constant factor  is the best possible. We named (1.2) Hardy-Hilbert's inequality. In 1934, Hardy et al. [3] gave some applications of (1.1)-(1.2) and a basic theorem with the general kernel (see [3, Theorem 318]).
is the best possible. We named (1.2) Hardy-Hilbert's inequality. In 1934, Hardy et al. [3] gave some applications of (1.1)-(1.2) and a basic theorem with the general kernel (see [3, Theorem 318]).
Theorem 1.
Suppose that  is a homogeneous function of
is a homogeneous function of  -degree, and
-degree, and  is a positive number. If both
is a positive number. If both  and
and  are strictly decreasing functions for
are strictly decreasing functions for  ,
,  , and
, and  then one has the following equivalent inequalities:
then one has the following equivalent inequalities:


where the constant factors  and
and  are the best possible.
are the best possible.
Note.
Hardy did not prove this theorem in [3]. In particular, we find some classical Hilbert-type inequalities as,
(i)for  in (1.3), it reduces (1.2),
in (1.3), it reduces (1.2),
(ii)for  in (1.3), it reduces to (see [3, Theorem 341])
in (1.3), it reduces to (see [3, Theorem 341])

(iii)for  in (1.3), it reduces to (see [3, Theorem 342])
in (1.3), it reduces to (see [3, Theorem 342])

Hardy also gave some multiple extensions of (1.3) (see [3, Theorem 322]). About introducing one pair of nonconjugate exponents  in (1.1), Hardy et al. [3] gave that if
in (1.1), Hardy et al. [3] gave that if  then
then

In 1951, Bonsall [4] considered (1.7) in the case of general kernel; in 1991, Mitrinović et al. [5] summarized the above results.
In 2001, Yang [6] gave an extension of (1.1) as for 

where the constant  is the best possible (
is the best possible ( is the Beta function). For
is the Beta function). For  (1.8) reduces to (1.1). And Yang [7] also gave an extension of (1.2) as
(1.8) reduces to (1.1). And Yang [7] also gave an extension of (1.2) as

where the constant factor  is the best possible.
is the best possible.
In 2004, Yang [8] published the dual form of (1.2) as follows:

where  is the best possible. For
is the best possible. For  both (1.10) and (1.2) reduce to (1.1). It means that there are more than two different best extensions of (1.1). In 2005, Yang [9] gave an extension of (1.8)–(1.10) with two pairs of conjugate exponents
both (1.10) and (1.2) reduce to (1.1). It means that there are more than two different best extensions of (1.1). In 2005, Yang [9] gave an extension of (1.8)–(1.10) with two pairs of conjugate exponents  , and two parameters
, and two parameters  as
as

where the constant factor  is the best possible; Krnić and Pečarić [10] also considered (1.11) in the general homogeneous kernel, but the best possible property of the constant factor was not proved by [10].
is the best possible; Krnić and Pečarić [10] also considered (1.11) in the general homogeneous kernel, but the best possible property of the constant factor was not proved by [10].
Note.
For  in [10, inequality (37)], it reduces to the equivalent result of (3.1) in this paper.
in [10, inequality (37)], it reduces to the equivalent result of (3.1) in this paper.
In 2006-2007, some authors also studied the operator expressing of (1.3) and (1.4).
Suppose that  is a symmetric function with
is a symmetric function with  and
and  is a positive number independent of
is a positive number independent of  Define an operator
Define an operator  as follows. For
as follows. For  there exists only
there exists only  satisfying
satisfying

Then the formal inner product of  and
and  are defined as follows:
are defined as follows:

In 2007, Yang [11] proved that if for  small enough,
small enough,  is strictly decreasing for
is strictly decreasing for  the integral
the integral  is also a positive number independent of
is also a positive number independent of  and
and

then  in this case, if
in this case, if  then we have two equivalent inequalities as
then we have two equivalent inequalities as

where the constant factor  is the best possible. In particular, for
is the best possible. In particular, for  being
being  -degree homogeneous, inequalities (1.15) reduce to (1.3)-(1.4) (in the symmetric kernel). Yang [12] also considered (1.15) in the real space
-degree homogeneous, inequalities (1.15) reduce to (1.3)-(1.4) (in the symmetric kernel). Yang [12] also considered (1.15) in the real space  .
.
In this paper, by using the way of weight coefficient and the theory of operators, we define a new Hilbert-type operator and obtain its norm. As applications, an extended basic theorem on Hilbert-type inequalities with the decreasing homogeneous kernel of  -degree is established; some particular cases are considered.
-degree is established; some particular cases are considered.
2. On a New Hilbert-Type Operator and the Norm
If  is a measurable function, satisfying for
is a measurable function, satisfying for  then we call
then we call  the homogeneous function of
the homogeneous function of  -degree.
-degree.
For  setting
setting  we find
we find  Hence, the following two words are equivalent: (a)
Hence, the following two words are equivalent: (a)  is decreasing in
is decreasing in  and strictly decreasing in a subinterval of
and strictly decreasing in a subinterval of  ; (b) for any
; (b) for any  ,
,  is decreasing in
is decreasing in  and strictly decreasing in a subinterval of
and strictly decreasing in a subinterval of  . The following two words are also equivalent:
. The following two words are also equivalent:  is decreasing in
is decreasing in  and strictly decreasing in a subinterval of
and strictly decreasing in a subinterval of  ;
;  for any
for any  ,
,  is decreasing in
is decreasing in  and strictly decreasing in a subinterval of
and strictly decreasing in a subinterval of  .
.
Lemma 2.1.
If  is decreasing in
is decreasing in  and strictly decreasing in a subinterval of
and strictly decreasing in a subinterval of  , and
, and  then
then

Proof.
By the assumption, we find  and there exists
and there exists  such that
such that  Hence,
Hence,

Lemma 2.2.
If  is a homogeneous function of
is a homogeneous function of  -degree, and
-degree, and  is a positive number, then (i)
is a positive number, then (i) (ii) for
(ii) for  setting the weight functions as
setting the weight functions as

then  .
.
Proof.
-
(i)
Setting
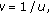 by the assumption, we obtain
by the assumption, we obtain 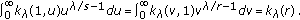 (ii) Setting
(ii) Setting 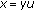 and
and 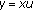 in the integrals
in the integrals 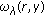 and
and 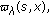 respectively, in view of (i), we still find that
respectively, in view of (i), we still find that 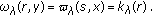
For  we set
we set  and
and  Define the real space as
Define the real space as  and then we may also define the spaces
and then we may also define the spaces  and
and 
Lemma 2.3.
As the assumption of Lemma 2.2, for  setting
setting  , if
, if  and
and  are decreasing in
are decreasing in  and strictly decreasing in a subinterval of
and strictly decreasing in a subinterval of  , then
, then 
Proof.
By Hölder's inequality [13] and Lemmas 2.1-2.2, we obtain

Therefore,  .
.
For  define a Hilbert-type operator
define a Hilbert-type operator  as
as  satisfying
satisfying 

In view of Lemma 2.3,  and then
and then  exists. If there exists
exists. If there exists  such that for any
such that for any  then
then  is bounded and
is bounded and  Hence by (2.4), we find
Hence by (2.4), we find  and
and  is bounded.
is bounded.
Theorem 2.4.
As the assumption of Lemma 2.3, it follows 
Proof.
For  by Hölder's inequality [12], we find
by Hölder's inequality [12], we find

Then by (2.4), we obtain

For  setting
setting  ,
,  as
as  for
for  if there exists a constant
if there exists a constant  such that (2.7) is still valid when we replace
such that (2.7) is still valid when we replace  by
by  then by Lemma 2.1,
then by Lemma 2.1,


In view of (2.8) and (2.9), setting  , by Fubini's theorem [13], it follows
, by Fubini's theorem [13], it follows

Setting  in the above inequality, by Fatou's lemma [14], we find
in the above inequality, by Fatou's lemma [14], we find

Hence  is the best value of (2.7). We conform that
is the best value of (2.7). We conform that  is the best value of (2.4). Otherwise, we can get a contradiction by (2.6) that the constant factor in (2.7) is not the best possible. It follows that
is the best value of (2.4). Otherwise, we can get a contradiction by (2.6) that the constant factor in (2.7) is not the best possible. It follows that 
3. An Extended Basic Theorem on Hilbert-Type Inequalities
Still setting  , and
, and 
 we have the following theorem.
we have the following theorem.
Theorem 3.1.
Suppose that  is a homogeneous function of
is a homogeneous function of  -degree,
-degree,  is a positive number, both
is a positive number, both  and
and  are decreasing in
are decreasing in  and strictly decreasing in a subinterval of
and strictly decreasing in a subinterval of  . If
. If  ,
,  then one has the equivalent inequalities as
then one has the equivalent inequalities as


where the constant factors  and
and  are the best possible.
are the best possible.
Proof.
In view of (2.7) and (2.4), we have (3.1) and (3.2). Based on Theorem 2.4, it follows that the constant factors in (3.1) and (3.2) are the best possible.
If (3.2) is valid, then by (2.6), we have (3.1). Suppose that (3.1) is valid. By (2.4),  If
If  then (3.2) is naturally valid; if
then (3.2) is naturally valid; if  setting
setting  then
then  By (3.1), we obtain
By (3.1), we obtain

and we have (3.2). Hence (3.1) and (3.2) are equivalent.
Remark 3.2.
-
(a)
For
 (3.1) and (3.2) reduce, respectively, to (1.6) and (1.7). Hence, Theorem 3.1 is an extension of Theorem A.
(3.1) and (3.2) reduce, respectively, to (1.6) and (1.7). Hence, Theorem 3.1 is an extension of Theorem A. -
(b)
Replacing the condition "
 and
and 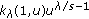 are decreasing in
are decreasing in 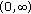 and strictly decreasing in a subinterval of
and strictly decreasing in a subinterval of 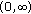 " by "for
" by "for 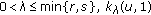 and
and  are decreasing in
are decreasing in  and strictly decreasing in a subinterval of
and strictly decreasing in a subinterval of 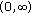 ," the theorem is still valid. Then in particular,
," the theorem is still valid. Then in particular,
(i)for  (
( ) in (3.1), we find
) in (3.1), we find

and then it deduces to (1.11);
(ii)for  in (3.1), we find
in (3.1), we find

and then it deduces to the best extension of (1.5) as

(iii)for  in (3.1), we find [3]
in (3.1), we find [3]

and  , and then it deduces to the best extension of (1.6) as
, and then it deduces to the best extension of (1.6) as

References
Weyl H: Singulare Integralgleichungen mit besonderer Beriicksichtigung des Fourierschen Integraltheorems, Inaugeral dissertation. University of Göttingen, Göttingen, Germany; 1908.
Hardy GH: Note on a theorem of Hilbert concerning series of positive terms. Proceedings of the London Mathematical Society 1925,23(2):45–46.
Hardy GH, Littlewood JE, Pólya G: Inequalities. Cambridge University Press, Cambridge, UK; 1934.
Bonsall FF: Inequalities with non-conjugate parameters. The Quarterly Journal of Mathematics 1951,2(1):135–150. 10.1093/qmath/2.1.135
Mitrinović DS, Pečarić JE, Fink AM: Inequalities Involving Functions and Their Integrals and Derivatives, Mathematics and Its Applications (East European Series). Volume 53. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1991:xvi+587.
Yang B: A generalization of the Hilbert double series theorem. Journal of Nanjing University Mathematical Biquarterly 2001,18(1):145–152.
Yang B: An extension of Hardy-Hilbert's inequality. Chinese Annals of Mathematics. Series A 2002,23(2):247–254.
Yang B: On new extensions of Hilbert's inequality. Acta Mathematica Hungarica 2004,104(4):291–299.
Yang B: On best extensions of Hardy-Hilbert's inequality with two parameters. Journal of Inequalities in Pure and Applied Mathematics 2005,6(3, article 81):1–15.
Krnić M, Pečarić J: General Hilbert's and Hardy's inequalities. Mathematical Inequalities & Applications 2005,8(1):28–51.
Yang B: On the norm of a Hilbert's type linear operator and applications. Journal of Mathematical Analysis and Applications 2007,325(1):529–541. 10.1016/j.jmaa.2006.02.006
Yang B: On the norm of a self-adjoint operator and applications to the Hilbert's type inequalities. Bulletin of the Belgian Mathematical Society 2006,13(4):577–584.
Kuang J: Applied Inequalities. Shandong Science and Technology Press, Jinan, China; 2004.
Kuang J: Introduction to Real Analysis. Hunan Education Press, Changsha, China; 1996.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yang, B. On a Hilbert-Type Operator with a Class of Homogeneous Kernels. J Inequal Appl 2009, 572176 (2009). https://doi.org/10.1155/2009/572176
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/572176
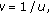 by the assumption, we obtain
by the assumption, we obtain 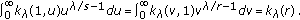 (ii) Setting
(ii) Setting 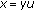 and
and 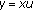 in the integrals
in the integrals 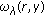 and
and 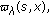 respectively, in view of (i), we still find that
respectively, in view of (i), we still find that 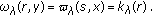
 (3.1) and (3.2) reduce, respectively, to (1.6) and (1.7). Hence, Theorem 3.1 is an extension of Theorem A.
(3.1) and (3.2) reduce, respectively, to (1.6) and (1.7). Hence, Theorem 3.1 is an extension of Theorem A. and
and 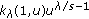 are decreasing in
are decreasing in 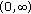 and strictly decreasing in a subinterval of
and strictly decreasing in a subinterval of 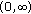 " by "for
" by "for 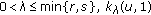 and
and  are decreasing in
are decreasing in  and strictly decreasing in a subinterval of
and strictly decreasing in a subinterval of 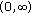 ," the theorem is still valid. Then in particular,
," the theorem is still valid. Then in particular,