- Research Article
- Open access
- Published:
Numerical Radius and Operator Norm Inequalities
Journal of Inequalities and Applications volume 2009, Article number: 492154 (2009)
Abstract
A general inequality involving powers of the numerical radius for sums and products of Hilbert space operators is given. This inequality generalizes several recent inequalities for the numerical radius, and includes that if  and
and  are operators on a complex Hilbert space
are operators on a complex Hilbert space  , then
, then  for
for  . It is also shown that if
. It is also shown that if  is normal
is normal  , then
, then  . Related numerical radius and usual operator norm inequalities for sums and products of operators are also presented.
. Related numerical radius and usual operator norm inequalities for sums and products of operators are also presented.
1. Introduction
Let  be a complex Hilbert space with inner product
be a complex Hilbert space with inner product  , and let
, and let  denote the
denote the  - algebra of all bounded linear operators on
- algebra of all bounded linear operators on  . For
. For  , the usual operator norm of an operator
, the usual operator norm of an operator  is defined by
is defined by

where  .
.
The numerical range of  , known also as the field of values of
, known also as the field of values of  , is defined as the set of complex numbers given by
, is defined as the set of complex numbers given by

The most important properties of the numerical range are that it is convex and its closure contains the spectrum of the operator.
A unitarily invariant norm  on
on  is a norm on the ideal
is a norm on the ideal  of
of  , satisfying
, satisfying  for all
for all  and all unitary operators
and all unitary operators  and
and  in
in  . It is called weakly unitarily invariant norm (or invariant under similarities) if
. It is called weakly unitarily invariant norm (or invariant under similarities) if  for all
for all  and all unitary operators
and all unitary operators  .
.
The most familiar example of weakly unitarily invariant norm is the numerical radius  defined by
defined by

It is well known that  defines a norm on
defines a norm on  and for every
and for every  , we have
, we have

Thus, the usual operator norm and the numerical radius norm are equivalent. The inequalities in (1.4) are sharp: if  , then the first inequality becomes an equality, while the second inequality becomes an equality if
, then the first inequality becomes an equality, while the second inequality becomes an equality if  is normal. In fact, for a nilpotant operator
is normal. In fact, for a nilpotant operator  with
with  , Haagerup and Harpe [1] show that
, Haagerup and Harpe [1] show that  . In particular, when
. In particular, when  , we get the reverse inequality of the first inequality in (1.4). For a comprehensive account on the theory of the numerical range and numerical radius, the reader is referred to [2, 3]. A detailed study for the field of values of a matrix is given in [4].
, we get the reverse inequality of the first inequality in (1.4). For a comprehensive account on the theory of the numerical range and numerical radius, the reader is referred to [2, 3]. A detailed study for the field of values of a matrix is given in [4].
The inequalities in (1.4) have been improved considerably by Kittaneh in [5, 6]. It has been shown that if  , then
, then


where  is the absolute value of
is the absolute value of  . The second inequality in (1.5) refines the second inequality in (1.4). For diverse applications of these inequalities we refer to [5, 7].
. The second inequality in (1.5) refines the second inequality in (1.4). For diverse applications of these inequalities we refer to [5, 7].
Considerable generalizations of the first inequality in (1.5) and the second inequality in (1.6) have been established in [8] for the numerical radius of one operator and for the sum of two operators. It has been shown that if  ,
, , then
, then


for  and
and  . Other recent inequalities have been obtained in [9, 10], which are related to the Euclidean radius of two Hilbert space operators and
. Other recent inequalities have been obtained in [9, 10], which are related to the Euclidean radius of two Hilbert space operators and  -normal operators in Hilbert spaces, respectively.
-normal operators in Hilbert spaces, respectively.
A general numerical radius inequality has been proved by Kittaneh, it has been shown in [6] that if  , then
, then

for all  . In particular,
. In particular,

Usual operator norm inequalities for sums of operators have attracted the attention of several mathematicians. Some of these inequalities have been introduced in [3, 11]. It has been shown in [6] that if  and
and  are normal and
are normal and  , then
, then

Another important norm inequalities for unitarily invariant norms, which are related to (1.11) assert that if  are positive and
are positive and  , then
, then


(see, e.g., [12]).
In Section 2 of this paper, we establish a general numerical radius inequality that generalizes (1.6), (1.7), (1.8), and (1.9), from which numerical radius inequalities for sums, products, and commutators of operators are obtained. Usual operator norm inequalities that generalize (1.11) and related to (1.13) are presented in Section 3.
2. A General Numerical Radius Inequality
In this section, we establish a general numerical radius inequality for Hilbert space operators which yields well known and new numerical radius inequalities as special cases. To prove our generalized inequality, we need the following basic lemmas. The first lemma is a generalized form of the mixed Schwarz inequality, which has been proved by Kittaneh [13].
Lemma 2.1.
Let  be an operator in
be an operator in  , and let
, and let  and
and  be nonnegative functions on
be nonnegative functions on  which are continuous and satisfy the relation
which are continuous and satisfy the relation  for all
for all  Then
Then

for all  and
and  in
in  .
.
The second lemma, which is called Hölder-McCarthy inequality, is a well-known result that follows from the spectral theorem for positive operators and Jensen's inequality (see [13]).
Lemma 2.2.
Let  be a positive operator in
be a positive operator in  and let
and let  be any unit vector. Then
be any unit vector. Then

The third lemma concerned with positive real numbers, and it is a consequence of the convexity of the function  ,
,  .
.
Lemma 2.3.
Let  be a positive real number
be a positive real number  Then
Then

The fourth lemma is a norm inequality for the sum of two operators, which can be found in [14].
Lemma 2.4.
If  and
and  are positive operators in
are positive operators in  , then
, then

Another important usual operator norm inequality which will be used in this section says that for any positive operators  ,
, we have (see [11])
we have (see [11])

Our main result of this paper, which leads to a generalization of (1.6), (1.7), (1.8), and (1.9), can be stated as follows.
Theorem 2.5.
Let  ,
, ,
, , and let
, and let  and
and  be nonnegative functions on
be nonnegative functions on  which are continuous and satisfy the relation
which are continuous and satisfy the relation  for all
for all  . Then
. Then

for all  .
.
Proof.
For every unit vector  , we have
, we have

Now the result follows by taking the supremum over all unit vectors in  .
.
Inequality (2.6) includes several numerical radius inequalities as special cases. Samples of inequalities are demonstrated in what follows.
For  and
and  ,
,  , in inequality (2.6), we get the following inequality that generalizes (1.9).
, in inequality (2.6), we get the following inequality that generalizes (1.9).
Corollary 2.6.
Let  ,
, ,
, ,
,  , and
, and  . Then
. Then

In particular,

For  in inequality (2.6), we get the following numerical radius inequalities for sums of operators that generalizes (1.8).
in inequality (2.6), we get the following numerical radius inequalities for sums of operators that generalizes (1.8).
Corollary 2.7.
Let  , and let
, and let  and
and  be as in Lemma 2.1. Then
be as in Lemma 2.1. Then

In particular,

It should be mentioned here that the inequality in (2.11) generalizes (1.7) in the case  .
.
Remark 2.8.
The case  in (2.11) gives
in (2.11) gives

which generalizes the second inequality in (1.6), while the choice  will give a generalization of the first inequality in (1.5) and can be stated as
will give a generalization of the first inequality in (1.5) and can be stated as

Note that using (2.4) and (2.5), a related inequality can be derived from (2.13). Indeed,

The above inequality generalizes the second inequality in (1.5). In fact, for  , we have
, we have

The last equality can be proved using the polar decomposition. In fact, if  and
and  are the polar decompositions of
are the polar decompositions of  and
and  , respectively, then
, respectively, then  .
.
It is known that  . However, the numerical radius is not submultiplicative, even for commuting operators. On the other hand, we have the power inequality, which asserts that if
. However, the numerical radius is not submultiplicative, even for commuting operators. On the other hand, we have the power inequality, which asserts that if  , then
, then

It is evident from the first inequality in (1.4) that if  , then
, then

Moreover, if  , then
, then

These inequalities, among other related ones, can be found in [2].
For  in inequality (2.6), we get the following numerical radius inequalities for products of operators that are related to the above inequalities.
in inequality (2.6), we get the following numerical radius inequalities for products of operators that are related to the above inequalities.
Corollary 2.9.
Let  ,
, and
and  . Then
. Then

In particular,

Remark 2.10.
The case  in (2.19), provides the following inequality
in (2.19), provides the following inequality

which is a numerical radius inequality for the product of operators and is related to the arithmetic-geometric mean inequality for operators. Note that a more general inequality can be obtained by letting  and
and  in (2.8). In fact, we have
in (2.8). In fact, we have

For  in (2.22), we obtain the inequality
in (2.22), we obtain the inequality

as well as

which follows from the the arithmetic-geometric mean inequality for operators (see [15]). Inequalities (2.23) and (2.24) are not equivalent. This can be seen from the example  ,
,  ,
,  .
.
The inequality in (2.22) can be used to give an upper bound for the numerical radius of  and
and  . In fact, we have
. In fact, we have


The commutator of  and
and  is the operator
is the operator  . Commutators play an important role in operator theory. It follows by the triangle inequality that if
. Commutators play an important role in operator theory. It follows by the triangle inequality that if  , then
, then  .
.
For  in inequality (2.6), we get the following numerical radius inequalities that generalize (1.9), and give an estimate for the numerical radius of commutators.
in inequality (2.6), we get the following numerical radius inequalities that generalize (1.9), and give an estimate for the numerical radius of commutators.
Corollary 2.11.
Let  , and let
, and let  and
and  be as in Theorem 2.5. Then
be as in Theorem 2.5. Then

for  . In particular,
. In particular,

We end this section by the following remark.
Remark 2.12.
Inequality (2.28) gives a numerical radius inequality for commutators of operators that generalizes (1.10). If  ,
,  , and
, and  , then
, then

In particular,

In fact, by letting  in (2.29) and (2.30), respectively, we get the following inequalities for the generalized commutator and the self commutator
in (2.29) and (2.30), respectively, we get the following inequalities for the generalized commutator and the self commutator


3. A General Norm Inequality
In this section, we introduce a general norm inequality for Hilbert space operators, from which new inequalities for operators and generalizations of earlier results can be derived. The proof of this general inequality is similar to that of Theorem 2.5 under slight modification.
Theorem 3.1.
Let  ,
, ,
, , and let
, and let  and
and  be as in Theorem 2.5. Then
be as in Theorem 2.5. Then

for 
Inequality (3.1) yields several norm inequalities as special cases. Samples of these inequalities are demonstrated below.
Corollary 3.2.
Let  ,
, ,
, ,
,  , and
, and  . Then
. Then

In particular,

For  in inequality (3.2), we get the following operator inequalities for sums of operators.
in inequality (3.2), we get the following operator inequalities for sums of operators.
Corollary 3.3.
Let  ,
,  , and
, and  . Then
. Then

In particular, if  is normal
is normal  , then
, then

Remark 3.4.
The inequality (3.5) is a generalized form of (1.11). The normality of  is necessary, this inequality is not true for arbitrary operators
is necessary, this inequality is not true for arbitrary operators  , as may be seen for
, as may be seen for  and
and  .
.
For  in inequality (3.2), we get norm inequalities for products of operators.
in inequality (3.2), we get norm inequalities for products of operators.
Corollary 3.5.
Let  and
and  . Then
. Then

In particular,

For  in inequality (3.2), we get the following norm inequalities that give an estimate for the usual norm of commutators.
in inequality (3.2), we get the following norm inequalities that give an estimate for the usual norm of commutators.
Corollary 3.6.
Let  , and let
, and let  . Then
. Then

Finally, we end this paper by the following remark.
Remark 3.7.
Inequality (3.8) gives a norm inequality for commutators of operators. If  ,
,  , and
, and  , then we get
, then we get

In particular,

In fact, by letting  in (3.10), we get the following inequality for self commutator
in (3.10), we get the following inequality for self commutator

Moreover a related inequality to (3.11) can be derived from (1.12) and (1.13). Indeed,

References
Haagerup U, de la Harpe P: The numerical radius of a nilpotent operator on a Hilbert space. Proceedings of the American Mathematical Society 1992,115(2):371–379. 10.1090/S0002-9939-1992-1072339-6
Gustafson KE, Rao DKM: Numerical Range: The Field of Values of Linear Operators and Matrices, Universitext. Springer, New York, NY, USA; 1997:xiv+189.
Zhan X: Matrix Inequalities, Lecture Notes in Mathematics. Volume 1790. Springer, Berlin, Germany; 2002:viii+116.
Horn RA, Johnson CR: Topics in Matrix Analysis. Cambridge University Press, Cambridge, UK; 1991:viii+607.
Kittaneh F: A numerical radius inequality and an estimate for the numerical radius of the Frobenius companion matrix. Studia Mathematica 2003,158(1):11–17. 10.4064/sm158-1-2
Kittaneh F: Numerical radius inequalities for Hilbert space operators. Studia Mathematica 2005,168(1):73–80. 10.4064/sm168-1-5
Kittaneh F: Bounds for the zeros of polynomials from matrix inequalities. Archiv der Mathematik 2003,81(5):601–608. 10.1007/s00013-003-0525-6
El-Haddad M, Kittaneh F: Numerical radius inequalities for Hilbert space operators. II. Studia Mathematica 2007,182(2):133–140. 10.4064/sm182-2-3
Dragomir SS: Some inequalities for the Euclidean operator radius of two operators in Hilbert spaces. Linear Algebra and Its Applications 2006,419(1):256–264. 10.1016/j.laa.2006.04.017
Dragomir SS, Moslehian MS: Some inequalities for
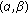 -normal operators in Hilbert spaces Facta Universitatis. Series: Mathematics and Informatics 2008, 23: 39–47.
-normal operators in Hilbert spaces Facta Universitatis. Series: Mathematics and Informatics 2008, 23: 39–47.Bhatia R: Matrix Analysis, Graduate Texts in Mathematics. Volume 169. Springer, Berlin, Germany; 1997:xii+347.
Shebrawi K, Albadawi H: Operator norm inequalities of Minkowski type. Journal of Inequalities in Pure and Applied Mathematics 2008,9(1, article 26):1–10.
Kittaneh F: Notes on some inequalities for Hilbert space operators. Publications of the Research Institute for Mathematical Sciences 1988,24(2):283–293. 10.2977/prims/1195175202
Kittaneh F: Norm inequalities for certain operator sums. Journal of Functional Analysis 1997,143(2):337–348. 10.1006/jfan.1996.2957
Kittaneh F: A note on the arithmetic-geometric-mean inequality for matrices. Linear Algebra and Its Applications 1992, 171: 1–8.
Acknowledgment
The authors thank the anonymous referee for his valuable comments and suggestions for improving this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Shebrawi, K., Albadawi, H. Numerical Radius and Operator Norm Inequalities. J Inequal Appl 2009, 492154 (2009). https://doi.org/10.1155/2009/492154
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/492154
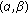 -normal operators in Hilbert spaces Facta Universitatis. Series: Mathematics and Informatics 2008, 23: 39–47.
-normal operators in Hilbert spaces Facta Universitatis. Series: Mathematics and Informatics 2008, 23: 39–47.