- Research Article
- Open access
- Published:
On an Extension of Shapiro's Cyclic Inequality
Journal of Inequalities and Applications volume 2009, Article number: 491576 (2009)
Abstract
We prove an interesting extension of the Shapiro's cyclic inequality for four and five variables and formulate a generalization of the well-known Shapiro's cyclic inequality. The method used in the proofs of the theorems in the paper concerns the positive quadratic forms.
1. Introduction
In 1954, Harold Seymour Shapiro proposed the inequality for a cyclic sum in  variables as follows:
variables as follows:

where  ,
,  and
and  for
for  . Although (1.1) was settled in 1989 by Troesch [1], the history of long year proofs of this inequality was interesting, and the certain problems remain (see [1–8]). Motivated by the directions of generalizations and proofs of (1.1), we consider the following inequality:
. Although (1.1) was settled in 1989 by Troesch [1], the history of long year proofs of this inequality was interesting, and the certain problems remain (see [1–8]). Motivated by the directions of generalizations and proofs of (1.1), we consider the following inequality:

where  and
and  . It is clear that (1.2) is true for
. It is clear that (1.2) is true for  . Indeed, by the Cauchy inequality, we have
. Indeed, by the Cauchy inequality, we have

It follows that

Obviously, (1.2) is true for every  if
if  or
or  .
.
In this note, by studying (1.2) in the case  , we show that it is true when
, we show that it is true when  , and false when
, and false when  . Moreover, we give a sufficient condition of
. Moreover, we give a sufficient condition of  ,
,  under which (1.2) is true in the case
under which (1.2) is true in the case  . It is worth saying that if
. It is worth saying that if  , then (1.2) is false for every even
, then (1.2) is false for every even  . Two open questions are discussed at the end of this paper.
. Two open questions are discussed at the end of this paper.
2. Main Result
Without loss generality of (1.2), we assume that  . However, (1.2) for
. However, (1.2) for  now is of the form
now is of the form

Theorem 2.1.
It holds that (2.1) is true for  , and it is false for
, and it is false for  .
.
Proof.
By the Cauchy inequality, we have

Hence

It is an equality if and only if

Consider the following quadratic form:

By a simple calculation we obtain the canonical quadratic form  as follows:
as follows:

where

It is easily seen that if  , that is,
, that is,  , then
, then  for all
for all  . This implies that
. This implies that  is positive. We thus have
is positive. We thus have  .
.
Now let us consider the cases when  vanishes. This depends considerably on the comparison of
vanishes. This depends considerably on the comparison of  with
with  . If
. If  , that is,
, that is,  , then the quadratic form
, then the quadratic form  attains
attains  at
at  and
and  . By (2.4) we assert that
. By (2.4) we assert that  whenever
whenever  and
and  . Also, if
. Also, if  , then
, then  vanishes if and only if
vanishes if and only if

Combining these facts with (2.4) we conclude that  when
when  .
.
Now we give a counter-example to (2.1) in the case  , that is,
, that is,  . Let
. Let  ,
,  , and
, and  . We will prove that
. We will prove that

It is obvious that

The last inequality is evident as  and
and  , so (2.9) follows.
, so (2.9) follows.
The theorem is proved.
Remark 2.2.
Let  denote the matrix of the quadratic form
denote the matrix of the quadratic form  in the canonical base of the real vector space
in the canonical base of the real vector space  . Namely,
. Namely,

Let  ,
,  ,
,  and
and  be the principal minors of orders
be the principal minors of orders  ,
,  ,
,  and
and  respectively, of
respectively, of  . By direct calculation we obtain
. By direct calculation we obtain

Then  is positive if and only if
is positive if and only if  for every
for every  . We find the first part of Theorem 2.1.
. We find the first part of Theorem 2.1.
Thanks to the idea of using positive quadratic form we now study (1.2) in the case  . It is sufficient to consider the case
. It is sufficient to consider the case  . By the Cauchy inequality, we reduce our work to the following inequality
. By the Cauchy inequality, we reduce our work to the following inequality

The matrix of  in an appropriate system of basic vectors is of the form
in an appropriate system of basic vectors is of the form

which has the principal minors

This implies that the necessary and sufficient condition for the positivity of the quadratic form  is
is

We thus obtain a sufficient condition under which (1.2) holds for  .
.
Theorem 2.3.
If  , then (1.2) is true for
, then (1.2) is true for  .
.
Remark 2.4.
Consider (1.2) in the case  ,
,  is even, and
is even, and  . According to the proof of the second part of Theorem 2.1, this inequality is false. Indeed, we choose
. According to the proof of the second part of Theorem 2.1, this inequality is false. Indeed, we choose  ,
,  . By the above counter-example, we conclude
. By the above counter-example, we conclude  .
.
Open Question 2 s.
-
(a)
Find pairs of nonnegative numbers
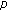 ,
, 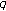 so that (1.2) is true for every
so that (1.2) is true for every 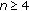 .
. -
(b)
For certain
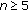 , which is sufficient condition of the pair
, which is sufficient condition of the pair  ,
, 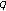 so that (1.2) is true.
so that (1.2) is true.
References
Troesch BA: The validity of Shapiro's cyclic inequality. Mathematics of Computation 1989,53(188):657–664.
Bushell PJ: Shapiro's cyclic sum. The Bulletin of the London Mathematical Society 1994,26(6):564–574. 10.1112/blms/26.6.564
Bushell PJ, McLeod JB: Shapiro's cyclic inequality for even . Journal of Inequalities and Applications 2002,7(3):331–348. 10.1155/S1025583402000164
Diananda PH: On a cyclic sum. Proceedings of the Glasgow Mathematical Association 1963, 6: 11–13. 10.1017/S2040618500034626
Drinfeld VG: A certain cyclic inequality. Mathematical Notes 1971, 9: 68–71. 10.1007/BF01316982
Fink AM: Shapiro's inequality. In Recent Progress in Inequalities, Mathematics and Its Applications, Part 13. Volume 430. 1st edition. Edited by: Milovanovic GV. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1997:241–248.
Mordell LJ: On the inequality
 and some others Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 1958, 22: 229–241. 10.1007/BF02941955
and some others Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 1958, 22: 229–241. 10.1007/BF02941955Mordell LJ: Note on the inequality
 and some others Journal of the London Mathematical Society 1962, 37: 176–178. 10.1112/jlms/s1-37.1.176
and some others Journal of the London Mathematical Society 1962, 37: 176–178. 10.1112/jlms/s1-37.1.176
Acknowledgment
This work is supported partially by Vietnam National Foundation for Science and Technology Development.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Tuan, N.M., Thuong, L.Q. On an Extension of Shapiro's Cyclic Inequality. J Inequal Appl 2009, 491576 (2009). https://doi.org/10.1155/2009/491576
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/491576
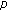 ,
, 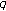 so that (1.2) is true for every
so that (1.2) is true for every 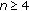 .
.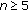 , which is sufficient condition of the pair
, which is sufficient condition of the pair  ,
, 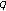 so that (1.2) is true.
so that (1.2) is true. and some others Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 1958, 22: 229–241. 10.1007/BF02941955
and some others Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 1958, 22: 229–241. 10.1007/BF02941955 and some others Journal of the London Mathematical Society 1962, 37: 176–178. 10.1112/jlms/s1-37.1.176
and some others Journal of the London Mathematical Society 1962, 37: 176–178. 10.1112/jlms/s1-37.1.176