- Research Article
- Open access
- Published:
On Solvability of a Generalized Nonlinear Variational-Like Inequality
Journal of Inequalities and Applications volume 2009, Article number: 467512 (2009)
Abstract
A new generalized nonlinear variational-like inequality is introduced and studied. By applying the auxiliary principle technique and KKM theory, we construct a new iterative algorithm for solving the generalized nonlinear variational-like inequality. By means of the Banach fixed-point theorem, we establish the existence and uniqueness of solution for the generalized nonlinear variational-like inequality. The convergence of the sequence generated by the iterative algorithm is also discussed.
1. Introduction
It is well known that variational inequality theory has become a very effective and powerful tool for studying a wide range of problems arising in many diverse fields. One of the most interesting and important problems in the variational inequality theory is the development of an efficient iterative algorithm to compute approximate solutions. The researchers in [1–10] suggested a lot of iterative algorithms for solving various variational inequalities and variational-like inequalities. By using the auxiliary principle technique, Ding and Yao [3], Ding et al. [4], Huang and Deng [5], Liu et al. [8, 9], and others studied several classes of nonlinear variational inequalities and variational-like inequalities in reflexive Banach and Hilbert spaces, respectively, suggested some iterative algorithms to compute approximate solutions for these nonlinear variational inequalities and variational-like inequalities, and proved the existence of solutions for the nonlinear variational inequalities and variational-like inequalities involving different monotone mappings.
Motivated and inspired by the research work in [1–10], we introduce and study a generalized nonlinear variational-like inequality. By using the auxiliary principle technique and KKM theorem due to Zhang and Xiang [2], we suggest a new iterative scheme for solving the generalized nonlinear variational-like inequality. Utilizing the Banach fixed-point theorem, we prove the existence and uniqueness of solution for the generalized nonlinear variational-like inequality. Under certain conditions, we discuss the convergence of the iterative sequence generalized by the iterative algorithm.
2. Preliminaries
Throughout this paper, let  be a real Hilbert space endowed with an inner product
be a real Hilbert space endowed with an inner product  and a norm
and a norm  , respectively, and
, respectively, and  . Let
. Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Assume that
. Assume that  is a coercive continuous bilinear form, that is, there exist positive constants
is a coercive continuous bilinear form, that is, there exist positive constants  such that
such that
(a1)
(a2) .
.
Remark 2.1.
It follows from (a1) and (a2) that 
Let  be nondifferentiable and satisfy the following conditions:
be nondifferentiable and satisfy the following conditions:
(b1) is linear in the first argument,
is linear in the first argument,
(b2) is convex in the second argument,
is convex in the second argument,
(b3) is bounded, that is, there exists a constant
is bounded, that is, there exists a constant  satisfying
satisfying

(b4)
Remark 2.2.
It follows that

which implies that  is continuous in the second argument.
is continuous in the second argument.
Let 
 be mappings and
be mappings and  . Now we consider the following generalized nonlinear variational-like inequality.
. Now we consider the following generalized nonlinear variational-like inequality.
Find  such that
such that

It is clear that for appropriate and suitable choices of the mappings  and
and  , the generalized nonlinear variational-like inequality (2.3) includes some variational inequalities and variational-like inequalities in [1–10] as special cases.
, the generalized nonlinear variational-like inequality (2.3) includes some variational inequalities and variational-like inequalities in [1–10] as special cases.
Recall the following concepts and results.
Definition 2.3.
Let 
 and
and  be mappings.
be mappings.
-
(1)

is said to beLipschitz continuous if there exists a constant
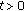 such that
such that

-
(2)
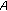
is said to be
 -relaxed Lipschitz if there exists a constant
-relaxed Lipschitz if there exists a constant 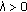 such that
such that

-
(3)
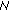
is said to be
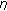 -strongly monotone with respect to
-strongly monotone with respect to 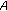 in the first argument if there exists a constant
in the first argument if there exists a constant  such that
such that

-
(4)
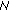
is said to be
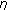 -monotone with respect to
-monotone with respect to 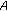 in the second argument if
in the second argument if

-
(5)
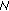
is said to be
 -relaxed cocoercive with respect to
-relaxed cocoercive with respect to 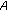 in the second argument if there exists a constant
in the second argument if there exists a constant  such that
such that

-
(6)
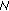
is said to beLipschitz continuous in the second argument if there exists a constant
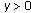 such that
such that

-
(7)

is said to beLipschitz continuous if there exists a constant
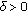 such that
such that

-
(8)

and
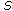 are said to be
are said to be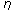 -hemicontinuous with respect to
-hemicontinuous with respect to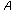 and
and in
in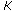 if for any
if for any , the mapping
, the mapping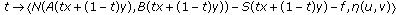 is continuous on
is continuous on
Lemma 2.4 (see [2]).
Let  be a nonempty closed convex subset of a Hausdorff linear topological space
be a nonempty closed convex subset of a Hausdorff linear topological space  , and let
, and let  be mappings satisfying the following conditions:
be mappings satisfying the following conditions:
(a) and
and 
(b)for each 
 is upper semicontinuous on
is upper semicontinuous on 
(c)for each  the set
the set  is a convex set;
is a convex set;
(d)there exists a nonempty compact set  and
and  such that
such that 
Then there exists  such that
such that 
Lemma 2.5 (see [11]).
Let 
 and
and  be nonnegative sequences satisfying
be nonnegative sequences satisfying

where

Then  .
.
Assumption 2.6.
Let  satisfy that
satisfy that
(1)
(2)for any  the mapping
the mapping  is convex and lower semicontinuous in
is convex and lower semicontinuous in 
3. Auxiliary Problem and Algorithm
Now we consider the following auxiliary problem with respect to the generalized nonlinear variational-like inequality (2.3). For each  find
find  such that
such that

where  is a constant.
is a constant.
Theorem 3.1.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  ,
, , and let
, and let  be Lipschitz continuous with constant
be Lipschitz continuous with constant  . Assume that
. Assume that  is a coercive continuous bilinear form satisfying (a1) and (a2),
is a coercive continuous bilinear form satisfying (a1) and (a2),  satisfies (b1)–(b4). Let
satisfies (b1)–(b4). Let  and
and  be mappings such that
be mappings such that  is Lipschitz continuous with constant
is Lipschitz continuous with constant  ,
,  is
is  -strongly monotone with respect to
-strongly monotone with respect to  in the first argument with constant
in the first argument with constant  ,
,  -relaxed cocoercive with respect to
-relaxed cocoercive with respect to  and Lipschitz continuous in the second argument with constants
and Lipschitz continuous in the second argument with constants  and
and  , respectively,
, respectively,  is
is  -relaxed Lipschitz with constant
-relaxed Lipschitz with constant  , and
, and  and
and  are
are  -hemicontinuous with respect to
-hemicontinuous with respect to  and
and  in
in  . Assume that Assumption 2.6 holds and there exists a positive constant
. Assume that Assumption 2.6 holds and there exists a positive constant  satisfying
satisfying

Then for each  , the auxiliary problem (3.1) has a unique solution in
, the auxiliary problem (3.1) has a unique solution in 
Proof.
Let  be in
be in  Define two functionals
Define two functionals  and
and  by
by

for all  .
.
Now we prove that the functionals  and
and  satisfy all the conditions of Lemma 2.4 in the weak topology. It is easy to see for all
satisfy all the conditions of Lemma 2.4 in the weak topology. It is easy to see for all 

which imply that  and
and  satisfy condition (a) of Lemma 2.4. Since
satisfy condition (a) of Lemma 2.4. Since  is a coercive continuous bilinear form,
is a coercive continuous bilinear form,  is convex and continuous in the second argument, and for given
is convex and continuous in the second argument, and for given  the mapping
the mapping  is convex and lower semicontinuous in
is convex and lower semicontinuous in  , it follows that for each
, it follows that for each  is weakly upper semicontinuous in the second argument and the set
is weakly upper semicontinuous in the second argument and the set  is convex for each
is convex for each  That is, the conditions (b) and (c) of Lemma 2.4 hold. Let
That is, the conditions (b) and (c) of Lemma 2.4 hold. Let 

Clearly,  is a weakly compact subset of
is a weakly compact subset of  . For each
. For each  we infer that
we infer that

which means that the condition (d) of Lemma 2.4 holds. Thus Lemma 2.4 ensures that there exists  such that
such that  for all
for all  that is,
that is,

Put  for
for  and
and  Replacing
Replacing  by
by  in (3.7), we obtain that
in (3.7), we obtain that

Notice that  is convex in the second argument. It follows from Assumption 2.6 and (3.8) that
is convex in the second argument. It follows from Assumption 2.6 and (3.8) that

which implies that

Letting  in (3.10), we conclude that
in (3.10), we conclude that

That is,  is a solution of the auxiliary problem (3.1).
is a solution of the auxiliary problem (3.1).
Now we prove the uniqueness of solution for the auxiliary problem (3.1). Suppose that  are two solutions of the auxiliary problem (3.1) with respect to
are two solutions of the auxiliary problem (3.1) with respect to  . It follows that
. It follows that


Taking  in (3.12) and
in (3.12) and  in (3.13), we get that
in (3.13), we get that


Adding (3.14) and (3.15), we deduce that

which yields that  by (3.2). That is,
by (3.2). That is,  is the unique solution of the auxiliary problem (3.1). This completes the proof.
is the unique solution of the auxiliary problem (3.1). This completes the proof.
The proof of the below result is similar to that of Theorem 3.1 and is omitted.
Theorem 3.2.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  ,
,  and
and  Lipschitz continuous with constant
Lipschitz continuous with constant  . Assume that
. Assume that  is a coercive continuous bilinear form satisfying (a1) and (a2),
is a coercive continuous bilinear form satisfying (a1) and (a2),  satisfies (b1)–(b4). Let
satisfies (b1)–(b4). Let  and
and  be mappings such that
be mappings such that  is
is  -strongly monotone with respect to
-strongly monotone with respect to  in the first argument with constant
in the first argument with constant  ,
,  -monotone with respect to
-monotone with respect to  in the second argument,
in the second argument,  is Lipschitz continuous with constant
is Lipschitz continuous with constant  and
and  and
and  are
are  -hemicontinuous with respect to
-hemicontinuous with respect to  and
and  in
in  . Assume that Assumption 2.6 holds and there exists a positive constant
. Assume that Assumption 2.6 holds and there exists a positive constant  satisfying
satisfying

Then for each  , the auxiliary problem (3.1) has a unique solution in
, the auxiliary problem (3.1) has a unique solution in 
Based on Theorems 3.1 and 3.2, we suggest the following iterative algorithm with errors for solving the generalized nonlinear variational-like inequality (2.3).
Algorithm 3.3.
For given  compute sequence
compute sequence  by the following iterative scheme:
by the following iterative scheme:

where  is a constant and
is a constant and  is a sequence in
is a sequence in  introduced to take into account possible inexact computation and satisfies that
introduced to take into account possible inexact computation and satisfies that

4. Existence and Convergence
In this section, we prove the existence of solution for the generalized nonlinear variational-like inequality (2.3) and discuss the convergence of the sequence generated by Algorithm 3.3.
Theorem 4.1.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  ,
, and
and  Lipschitz continuous with constant
Lipschitz continuous with constant  . Assume that
. Assume that  is a coercive continuous bilinear form satisfying (a1) and (a2),
is a coercive continuous bilinear form satisfying (a1) and (a2),  satisfies (b1)–(b4). Let
satisfies (b1)–(b4). Let  and
and  be mappings such that
be mappings such that  is Lipschitz continuous with constant
is Lipschitz continuous with constant  ,
,  is
is  -strongly monotone with respect to
-strongly monotone with respect to  in the first argument with constant
in the first argument with constant  ,
,  -relaxed cocoercive with respect to
-relaxed cocoercive with respect to  and Lipschitz continuous in the second argument with constants
and Lipschitz continuous in the second argument with constants  and
and  , respectively,
, respectively,  is
is  -relaxed Lipschitz with constant
-relaxed Lipschitz with constant  , and
, and  and
and  are
are  -hemicontinuous with respect to
-hemicontinuous with respect to  and
and  in
in  . Assume that Assumption 2.6 holds and
. Assume that Assumption 2.6 holds and

Then the generalized nonlinear variational-like inequality (2.3) possesses a unique solution  and the iterative sequence
and the iterative sequence  generated by Algorithm 3.3 converges strongly to
generated by Algorithm 3.3 converges strongly to 
Proof.
Note that (4.1) implies that (3.2) holds. It follows from Theorem 3.1 that there exists a mapping  such that for each
such that for each  is the unique solution of the auxiliary problem (3.1). Next we show that
is the unique solution of the auxiliary problem (3.1). Next we show that  is a contraction mapping in
is a contraction mapping in  . Let
. Let  and
and  be arbitrary elements in
be arbitrary elements in  and
and  a constant. Using (3.1), we deduce that
a constant. Using (3.1), we deduce that


Letting  in (4.2) and
in (4.2) and  in (4.3), and adding these inequalities, we arrive at
in (4.3), and adding these inequalities, we arrive at

that is,

where

by (4.1). Therefore,  is a contraction mapping. It follows from the Banach fixed-point theorem that
is a contraction mapping. It follows from the Banach fixed-point theorem that  has a unique fixed point
has a unique fixed point  In light of (3.1), we get that
In light of (3.1), we get that

which implies that

that is,  is a solution of the generalized nonlinear variational-like inequality (2.3).
is a solution of the generalized nonlinear variational-like inequality (2.3).
Now we prove the uniqueness. Suppose that the generalized nonlinear variational-like inequality (2.3) has two solutions  . It follows that
. It follows that


for all  Taking
Taking  in (4.9) and
in (4.9) and  in (4.10), we obtain that
in (4.10), we obtain that

Adding (4.11), we deduce that

which together with (4.1) implies that  That is, the generalized nonlinear variational-like inequality (2.3) has a unique solution in
That is, the generalized nonlinear variational-like inequality (2.3) has a unique solution in  .
.
Next we discuss the convergence of the iterative sequence generated by Algorithm 3.3. Taking  in (4.7) and
in (4.7) and  in (3.18), and adding these inequalities, we infer that
in (3.18), and adding these inequalities, we infer that

That is,

where  is defined by (4.6). It follows from (3.19), (4.1), (4.14), and Lemma 2.5 that the iterative sequence
is defined by (4.6). It follows from (3.19), (4.1), (4.14), and Lemma 2.5 that the iterative sequence  generated by Algorithm 3.3 converges strongly to
generated by Algorithm 3.3 converges strongly to  This completes the proof.
This completes the proof.
As in the proof of Theorem 4.1, we have the following theorem.
Theorem 4.2.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  ,
, and
and  Lipschitz continuous with constant
Lipschitz continuous with constant  . Assume that
. Assume that  is a coercive continuous bilinear form satisfying (a1) and (a2),
is a coercive continuous bilinear form satisfying (a1) and (a2),  satisfies (b1)–(b4). Let
satisfies (b1)–(b4). Let  and
and  be mappings such that
be mappings such that  is
is  -strongly monotone with respect to
-strongly monotone with respect to  in the first argument with constant
in the first argument with constant  ,
,  -monotone with respect to
-monotone with respect to  in the second argument,
in the second argument,  is Lipschitz continuous with constant
is Lipschitz continuous with constant  and
and  and
and  are
are  -hemicontinuous with respect to
-hemicontinuous with respect to  and
and  in
in  . Assume that Assumption 2.6 holds and
. Assume that Assumption 2.6 holds and

Then the generalized nonlinear variational-like inequality (2.3) possesses a unique solution  and the iterative sequence
and the iterative sequence  generated by Algorithm 3.3 converges strongly to
generated by Algorithm 3.3 converges strongly to 
Remark 4.3.
The conditions of Theorems 3.1, 3.2, 4.1, and 4.2 are different from the conditions of the results in [1–10]. In particular, the mappings  and
and  with respect to the second argument in Theorems 3.2 and 4.2 are Lipschitz continuous, but other mappings in Theorems 3.2 and 4.2 are not Lipschitz continuous.
with respect to the second argument in Theorems 3.2 and 4.2 are Lipschitz continuous, but other mappings in Theorems 3.2 and 4.2 are not Lipschitz continuous.
References
Ansari QH, Yao JC: Iterative schemes for solving mixed variational-like inequalities. Journal of Optimization Theory and Applications 2001,108(3):527–541. 10.1023/A:1017531323904
Zhang SS, Xiang SW: Existence of solutions for a class of quasibilinear variational inequalities. Journal of Systems Science and Mathematical Sciences 1996,16(2):136–140.
Ding XP, Yao J-C: Existence and algorithm of solutions for mixed quasi-variational-like inclusions in Banach spaces. Computers & Mathematics with Applications 2005,49(5–6):857–869. 10.1016/j.camwa.2004.05.013
Ding XP, Yao J-C, Zeng L-C: Existence and algorithm of solutions for generalized strongly nonlinear mixed variational-like inequalities in Banach spaces. Computers & Mathematics with Applications 2008,55(4):669–679. 10.1016/j.camwa.2007.06.004
Huang N, Deng C: Auxiliary principle and iterative algorithms for generalized set-valued strongly nonlinear mixed variational-like inequalities. Journal of Mathematical Analysis and Applications 2001,256(2):345–359. 10.1006/jmaa.2000.6988
Huang N-J, Fang Y-P: Auxiliary principle technique for solving generalized set-valued nonlinear quasi-variational-like inequalities. Mathematical Inequalities & Applications 2003,6(2):339–350.
Liu Z, Chen Z, Kang SM, Ume JS: Existence and iterative approximations of solutions for mixed quasi-variational-like inequalities in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2008,69(10):3259–3272. 10.1016/j.na.2007.09.015
Liu Z, Ume JS, Kang SM: General strongly nonlinear quasivariational inequalities with relaxed Lipschitz and relaxed monotone mappings. Journal of Optimization Theory and Applications 2002,114(3):639–656. 10.1023/A:1016079130417
Liu Z, Ume JS, Kang SM: Generalized nonlinear variational-like inequalities in reflexive Banach spaces. Journal of Optimization Theory and Applications 2005,126(1):157–174. 10.1007/s10957-005-2666-1
Yao JC: The generalized quasi-variational inequality problem with applications. Journal of Mathematical Analysis and Applications 1991,158(1):139–160. 10.1016/0022-247X(91)90273-3
Liu LS: Ishikawa and Mann iterative process with errors for nonlinear strongly accretive mappings in Banach spaces. Journal of Mathematical Analysis and Applications 1995,194(1):114–125. 10.1006/jmaa.1995.1289
Acknowledgments
This work was supported by the Science Research Foundation of Educational Department of Liaoning Province (2009A419) and the Korea Research Foundation(KRF) Grant funded by the Korea government (MEST) (2009-0073655).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liu, Z., Zheng, P., Ume, J.S. et al. On Solvability of a Generalized Nonlinear Variational-Like Inequality. J Inequal Appl 2009, 467512 (2009). https://doi.org/10.1155/2009/467512
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/467512

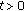 such that
such that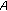
 -relaxed Lipschitz if there exists a constant
-relaxed Lipschitz if there exists a constant 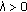 such that
such that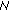
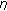 -strongly monotone with respect to
-strongly monotone with respect to 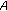 in the first argument if there exists a constant
in the first argument if there exists a constant  such that
such that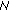
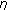 -monotone with respect to
-monotone with respect to 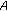 in the second argument if
in the second argument if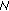
 -relaxed cocoercive with respect to
-relaxed cocoercive with respect to 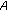 in the second argument if there exists a constant
in the second argument if there exists a constant  such that
such that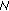
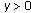 such that
such that
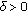 such that
such that
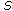 are said to be
are said to be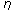 -hemicontinuous with respect to
-hemicontinuous with respect to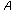 and
and in
in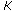 if for any
if for any , the mapping
, the mapping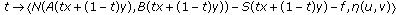 is continuous on
is continuous on