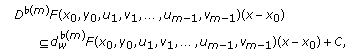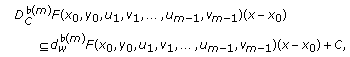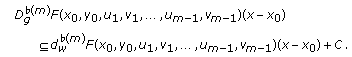- Research Article
- Open access
- Published:
Higher-Order Weakly Generalized Adjacent Epiderivatives and Applications to Duality of Set-Valued Optimization
Journal of Inequalities and Applications volume 2009, Article number: 462637 (2009)
Abstract
A new notion of higher-order weakly generalized adjacent epiderivative for a set-valued map is introduced. By virtue of the epiderivative and weak minimality, a higher-order Mond-Weir type dual problem and a higher-order Wolfe type dual problem are introduced for a constrained set-valued optimization problem, respectively. Then, corresponding weak duality, strong duality, and converse duality theorems are established.
1. Introduction
In the last several decades, several notions of derivatives of set-valued maps have been proposed and used for the formulation of optimality conditions and duality in set-valued optimization problems. By using a contingent epiderivative of a set-valued map, Jahn and Rauh [1] obtained a unified necessary and sufficient optimality condition. Chen and Jahn [2] introduced a notion of a generalized contingent epiderivative of a set-valued map and obtained a unified necessary and sufficient conditions for a set-valued optimization problem. Lalitha and Arora [3] introduced a notion of a weak Clarke epiderivative and use it to establish optimality criteria for a constrained set-valued optimization problem. On the other hand, various kinds of differentiable type dual problems for set-valued optimization problems, such as Mond-Weir type and Wolfe type dual problems, have been investigated. By virtue of the tangent derivative of a set-valued map introduced in [4], Sach and Craven [5] discussed Wolfe type duality and Mond-Weir type duality problems for a set-valued optimization problem. By virtue of the codifferential of a set-valued map introduced in [6], Sach et al. [7] obtained Mond-Weir type and Wolfe type weak duality and strong duality theorems of set-valued optimization problems. As to other concepts of derivatives (epiderivatives) of set-valued maps and their applications, one can refer to [8–15]. Recently, Second-order derivatives have also been proposed, for example, see [16, 17] and so on.
Since higher-order tangent sets introduced in [4], in general, are not cones and convex sets, there are some difficulties in studying higher-order optimality conditions and duality for general set-valued optimization problems. Until now, there are only a few papers to deal with higher-order optimality conditions and duality of set-valued optimization problems by virtue of the higher-order derivatives or epiderivatives introduced by the higher-order tangent sets. Li et al. [18] studied some properties of higher-order tangent sets and higher-order derivatives introduced in [4], and then obtained higher-order necessary and sufficient optimality conditions for set-valued optimization problems under cone-concavity assumptions. By using these higher-order derivatives, they also discussed a higher-order Mond-Weir duality for a set-valued optimization problem in [19]. Li and Chen [20] introduced higher-order generalized contingent(adjacent) epiderivatives of set-valued maps, and obtained higher-order Fritz John type necessary and sufficient conditions for Henig efficient solutions to a constrained set-valued optimization problem.
Motivated by the work reported in [3, 5, 18–20], we introduce a notion of higher-order weakly generalized adjacent epiderivative for a set-valued map. Then, by virtue of the epiderivative, we discuss a higher-order Mond-Weir type duality problem and a higher-order Wolfe type duality problem to a constrained set-valued optimization problem, respectively.
The rest of the paper is organized as follows. In Section 2, we collect some of the concepts and some of their properties required for the paper. In Section 3, we introduce a generalized higher-order adjacent set of a set and a higher-order weakly generalized adjacent epiderivative of a set-valued map, and study some of their properties. In Sections 4 and 5, we introduce a higher-order Mond-Weir type dual problem and a higher-order Wolfe type dual problem to a constrained set-valued optimization problem and establish corresponding weak duality, strong duality and converse duality theorems, respectively.
2. Preliminaries and Notations
Throughout this paper, let  , and
, and  be three real normed spaces, where the spaces
be three real normed spaces, where the spaces  and
and  are partially ordered by nontrivial pointed closed convex cones
are partially ordered by nontrivial pointed closed convex cones  and
and  with
with  and
and  , respectively. We assume that
, respectively. We assume that  denote the origins of
denote the origins of  , respectively,
, respectively,  denotes the topological dual space of
denotes the topological dual space of  and
and  denotes the dual cone of
denotes the dual cone of  , defined by
, defined by  . Let
. Let  be a nonempty set in
be a nonempty set in  . The cone hull of
. The cone hull of  is defined by
is defined by  . Let
. Let  be a nonempty subset of
be a nonempty subset of  ,
,  and
and  be two given nonempty set-valued maps. The effective domain, the graph and the epigraph of
be two given nonempty set-valued maps. The effective domain, the graph and the epigraph of  are defined respectively by
are defined respectively by 
 , and
, and  The profile map
The profile map  is defined by
is defined by  , for every
, for every  . Let
. Let  ,
, 
Definition 2.1.
An element  is said to be a minimal point
is said to be a minimal point  resp., weakly minimal point
resp., weakly minimal point of
of  if
if 
 resp.,
resp.,  . The set of all minimal point (resp., weakly minimal point) of
. The set of all minimal point (resp., weakly minimal point) of  is denoted by
is denoted by  (resp.,
(resp.,  .
.
Definition 2.2.
Let  be a set-valued map.
be a set-valued map.
(i) is said to be
is said to be  -convex on a convex set
-convex on a convex set  , if for any
, if for any  and
and  ,
,

(ii) is said to be
is said to be  -convex like on a nonempty subset
-convex like on a nonempty subset  , if for any
, if for any  and
and  , there exists
, there exists  such that
such that 
Remark 2.3.
(i)??If  is
is  -convex on a convex set
-convex on a convex set  , then
, then  is
is  -convex like on
-convex like on  . But the converse does not hold.
. But the converse does not hold.
(ii)?? If  is
is  -convex like on a nonempty subset
-convex like on a nonempty subset  , then
, then  is convex.
is convex.
Suppose that  is a positive integer,
is a positive integer,  is a normed space supplied with a distance
is a normed space supplied with a distance  and
and  is a subset of
is a subset of  . We denote by
. We denote by  the distance from
the distance from  to
to  , where we set
, where we set  .
.
Definition 2.4 (see [4]).
Let  belong to a subset K of a normed space
belong to a subset K of a normed space  and let
and let  be elements of
be elements of  . We say that the subset
. We say that the subset

is the  th-order adjacent set of
th-order adjacent set of  at
at 
From [18, Propositions ?3.2], we have the following result.
Proposition 2.5.
If  is convex,
is convex,  , and
, and  , then
, then 
 is convex.
is convex.
3. Higher-Order Weakly Generalized Adjacent Epiderivatives
Definition 3.1.
Let  belong to a subset K of
belong to a subset K of  and let
and let  be elements of
be elements of  . The subset
. The subset

is said to be the  th-order generalized adjacent set of
th-order generalized adjacent set of  at
at 
Definition 3.2.
The  th-order weakly generalized adjacent epiderivative
th-order weakly generalized adjacent epiderivative 
 of
of  at
at  with respect to
with respect to  vectors
vectors 
 is the set-valued map from
is the set-valued map from  to
to  defined by
defined by

The weak domination property  resp., domination property
resp., domination property is said to hold for a subset
is said to hold for a subset  of
of  if
if 
 resp.,
resp.,  .
.
To compare our derivative with well-known derivatives, we recall some notions.
Definition 3.4 (see [4]).
The  th-order adjacent derivative
th-order adjacent derivative 

 of
of  at
at  with respect to vectors
with respect to vectors  is the set-valued map from
is the set-valued map from  to
to  defined by
defined by

Definition 3.5 (see [19]).
The  -directed
-directed  th-order adjacent derivative
th-order adjacent derivative 
 of
of  at
at  with respect to vectors
with respect to vectors  is the
is the  th-order adjacent derivative of set-valued mapping
th-order adjacent derivative of set-valued mapping  at
at  with respect to
with respect to 
 .
.
Definition 3.6 (See [20]).
The  th-order generalized adjacent epiderivative
th-order generalized adjacent epiderivative 
 of
of  at
at  with respect to vectors
with respect to vectors  is the set-valued map from
is the set-valued map from  to
to  defined by
defined by

Using properties of higher-order adjacent sets [4], we have the following result.
Proposition 3.7.
Let  . If
. If  and the set
and the set  -
- fulfills the weak domination property for all
fulfills the weak domination property for all  , then for any
, then for any  ,
,
-
(i)
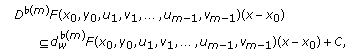 (3.5)
(3.5)
-
(ii)
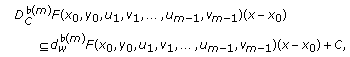 (3.6)
(3.6)
-
(iii)
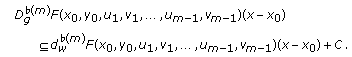 (3.7)
(3.7)
Remark 3.8.
The reverse inclusions in Proposition 3.7 may not hold. The following examples explain the case, where we only take  .
.
Example 3.9.
Let  ,
,  ,
,  and
and  . Then for any
. Then for any  ,
,  and
and  -
- Therefore, for any
Therefore, for any  ,
,  ,
,  and
and  do not exist, but
do not exist, but

Example 3.10.
Let  ,
,  ,
,  and
and  . Then,
. Then,  ,
,  -
- . Hence, for any
. Hence, for any  ,
,  ,
,  and
and 
 do not exist. But
do not exist. But

Example 3.11.
Suppose that  . Let
. Let  be a set-valued map with
be a set-valued map with 
 and
and  . Then
. Then  ,
,  -
- Therefore for any
Therefore for any  ,
,

Now we discuss some crucial propositions of the  th-order weakly generalized adjacent epiderivative.
th-order weakly generalized adjacent epiderivative.
Proposition 3.12.
Let  ,
,  ,
,  . If the set
. If the set  -
- fulfills the weak domination property for all
fulfills the weak domination property for all  , then for all
, then for all  ,
,

Proof.
Take any  and an arbitrary sequence
and an arbitrary sequence  with
with  . Since
. Since  ,
,

It follows from  , and
, and  is a convex cone that
is a convex cone that

We get

which implies that

that is,  . By the definition of
. By the definition of  th-order weakly generalized adjacent epiderivative and the weak domination property, we have
th-order weakly generalized adjacent epiderivative and the weak domination property, we have

Thus  .
.
Remark 3.13.
Since the cone-convexity and cone-concavity assumptions are omitted, Proposition 3.12 improves [18, Theorem  ] and [20, Proposition
] and [20, Proposition  ].
].
Proposition 3.14.
Let  be a nonempty convex subset of
be a nonempty convex subset of  ,
,  ,
,  . Let
. Let  be
be  -convex like on
-convex like on  ,
,  . If the set
. If the set  -
- fulfills the weak domination property for all
fulfills the weak domination property for all  , then
, then

Proof.
Take any  ,
,  and an arbitrary sequence
and an arbitrary sequence  with
with  . Since
. Since  is convex and
is convex and  be
be  -convex like on
-convex like on  , we get that
, we get that  is a convex subset and
is a convex subset and  is a convex cone. Therefore
is a convex cone. Therefore

It follows from  ,
,  is convex and
is convex and  is a convex cone that
is a convex cone that

We obtain that

which implies that

that is,  . By the definition of
. By the definition of  th-order weakly generalized adjacent epiderivative and the weak domination property, we have
th-order weakly generalized adjacent epiderivative and the weak domination property, we have

Thus  and the proof is complete.
and the proof is complete.
Remark 3.15.
Since the cone-convexity assumptions are replaced by cone-convex likeness assumptions, Proposition 3.14 improves [20, Proposition  ].
].
4. Higher-Order Mond-Weir Type Duality
In this section, we introduce a higher-order Mond-Weir type dual problem for a constrained set-valued optimization problem by virtue of the higher-order weakly generalized adjacent epiderivative and discuss its weak duality, strong duality and converse duality properties. The notation  is used to denote
is used to denote  . Firstly, we recall the definition of interior tangent cone of a set and state a result regarding it from [16].
. Firstly, we recall the definition of interior tangent cone of a set and state a result regarding it from [16].
The interior tangent cone of  at
at  is defined as
is defined as

where  stands for the closed ball centered at
stands for the closed ball centered at  and of radius
and of radius  .
.
Lemma 4.1 (see [16]).
If  is convex,
is convex,  and
and  , then
, then

Consider the following set-valued optimization problem:

Set  . A point
. A point  is said to be a feasible solution of
is said to be a feasible solution of  if
if  and
and  .
.
Definition 4.2.
A point  is said to be a weakly minimal solution of
is said to be a weakly minimal solution of  if
if  satisfying
satisfying  and
and  .
.
Suppose that  ,
,  ,
,  , and
, and  . We introduce a higher-order Mond-Weir type dual problem
. We introduce a higher-order Mond-Weir type dual problem of
of  as follows:
as follows:




Let  satisfy conditions
satisfy conditions (4.4)–(4.7)
(4.4)–(4.7) . A point
. A point 
 satisfying (4.4)–(4.7) is called a feasible solution of
satisfying (4.4)–(4.7) is called a feasible solution of  . A feasible solution
. A feasible solution 
 is called a weakly maximal solution of
is called a weakly maximal solution of  if
if  .
.
Theorem 4.3 (weak duality).
Let 
 and
and 
 . Let the set
. Let the set  -
-

 fulfill the weak domination property for all
fulfill the weak domination property for all  . If
. If  is a feasible solution of
is a feasible solution of  and
and  is a feasible solution of
is a feasible solution of  , then
, then

Proof.
It follows from Proposition 3.12 that

Since  is a feasible solution of
is a feasible solution of  ,
,  . Take
. Take  . Then, it follows from (4.5) and (4.7) that
. Then, it follows from (4.5) and (4.7) that

By (4.4), (4.6), (4.7), (4.9) and (4.10), we get

Thus, the proof is complete.
Remark 4.4.
In Theorem 4.3, cone-convexity assumptions of [19, Theorem ?4.1] are omitted.
By the similiar proof method of Theorem 4.3, it follows from Proposition 3.14 that the following theorem holds.
Theorem 4.5 (weak duality).
Let  ,
,  and
and  . Suppose that
. Suppose that  is
is  -convex like on a nonempty convext subset
-convex like on a nonempty convext subset  . Let the set
. Let the set  -
-

 fulfill the weak domination property for all
fulfill the weak domination property for all  . If
. If  is a feasible solution of
is a feasible solution of  and
and  is a feasible solution of
is a feasible solution of  , then
, then

Lemma 4.6.
Let  ,
,  ,
,  . Let the set
. Let the set  -
-


 fulfill the weak domination property for all
fulfill the weak domination property for all  . If
. If  is a weakly minimal solution of
is a weakly minimal solution of  , then
, then

for all 
Proof.
Since  is a weakly minimal solution of
is a weakly minimal solution of  ,
,  . Then,
. Then,

Assume that the result (4.13) does not hold. Then there exist  ,
,  and
and  with
with  such that
such that


It follows from (4.15) and the definition of  th-order weakly generalized adjacent epiderivative that
th-order weakly generalized adjacent epiderivative that

Thus, for an arbitrary sequence  with
with  , there exists a sequence
, there exists a sequence  such that
such that

From (4.16) and (4.18), there exists a sufficiently large  such that
such that


Since  ,
,  and
and  is a convex cone,
is a convex cone,

It follows from (4.19) and (4.21) that

By (4.20) and Lemma 4.1, we have  . Then, it follows from the definition of
. Then, it follows from the definition of  that
that  Since
Since  , there exists a sufficiently large
, there exists a sufficiently large  such that
such that

Then, from (4.20), we have

It follows from  , and
, and  is a convex cone that
is a convex cone that

Since  , there exist
, there exist  such that
such that  It follows from (4.25) that
It follows from (4.25) that  , for
, for  , and then
, and then

It follows from (4.22) that

which contradicts (4.14). Thus (4.13) holds and the proof is complete.
Theorem 4.7 (strong duality).
Suppose that  ,
,  and the following conditions are satisfied:
and the following conditions are satisfied:
(i) ,
,  ;
;
(ii) is
is  -convex like on a nonempty convex subset
-convex like on a nonempty convex subset  ;
;
(iii) is a weakly minimal solution of
is a weakly minimal solution of  ;
;
(iv) -
-
 fulfills the weak domination property for all
fulfills the weak domination property for all  and
and  ;
;
(v)There exists an  such that
such that  .
.
Then there exist  and
and  such that
such that  is a weakly maximal solution of
is a weakly maximal solution of  .
.
Proof.
Define

By the similar proof method for the convexity of  in [20, Theorem ?5.1], just replacing
in [20, Theorem ?5.1], just replacing  -order generalized adjacent epiderivative by
-order generalized adjacent epiderivative by  -order weakly generalized adjacent epiderivative, we have that
-order weakly generalized adjacent epiderivative, we have that  is a convex set. It follows from Lemma 4.6 that
is a convex set. It follows from Lemma 4.6 that

By the separation theorem of convex sets, there exist  and
and  , not both zero functionals, such that
, not both zero functionals, such that

It follows from (4.30) that


From (4.31), we obtain that  is bounded below on the
is bounded below on the  . Then,
. Then,  , for all
, for all  . Naturally,
. Naturally,  . By the similar proof method for
. By the similar proof method for  , we get
, we get  .
.
Now we show that  . Suppose that
. Suppose that  . Then
. Then  . By Proposition 3.14 and condition (v), there exists a point
. By Proposition 3.14 and condition (v), there exists a point  such that
such that  and
and

Thus it follows from (4.32) that  . Since
. Since  and
and  , we have
, we have  , which leads to a contradiction. So
, which leads to a contradiction. So  .
.
From (4.32) and assumption (iv), we have  . Since
. Since  and
and  ,
,  . Therefore
. Therefore

It follows from (4.32), (4.34),  and
and  that
that  , for all
, for all  So
So  is a feasible solution of
is a feasible solution of  .
.
Finally, we prove that  is a weakly maximal solution of
is a weakly maximal solution of  .
.
Suppose that  is not a weakly maximal solution of
is not a weakly maximal solution of  . Then there exists a feasible solution
. Then there exists a feasible solution  of
of  such that
such that

According to  , we get
, we get

Since  is a weakly minimal solution of
is a weakly minimal solution of  , it follows from Theorem 4.5 that
, it follows from Theorem 4.5 that

which contradicts (4.36). Thus the conclusion holds and the proof is complete.
Now we give an example to illustrate the Strong Duality. we only take  .
.
Example 4.8.
Let 
 . Let
. Let  be a set-valued map with
be a set-valued map with

and  be a set-valued map with
be a set-valued map with

Naturally,  is a
is a  -convex like map on the convex set
-convex like map on the convex set  .
.
Let  . Then
. Then  is a weakly minimal solution of
is a weakly minimal solution of  . Take
. Take  ,
,  . Then
. Then  ,
, 
 , for
, for  . The dual problem
. The dual problem  becomes
becomes

Therefore the conditions of Theorem 4.7 are satisfied. Simultaneous, take  and
and  . Obviously,
. Obviously,  is a feasible solution of
is a feasible solution of  . It follows from Theorem 4.5 that
. It follows from Theorem 4.5 that  is a weakly maximal solution of
is a weakly maximal solution of  .
.
Since neither of  and
and  is
is  -convex map on the
-convex map on the  , the assumptions of [19, Theorem ?4.3] are not satisfied. Therefore, [19, Theorem ?4.3] is unusable here.
, the assumptions of [19, Theorem ?4.3] are not satisfied. Therefore, [19, Theorem ?4.3] is unusable here.
Theorem 4.9 (converse duality).
Suppose that  ,
,  , and the following conditions are satisfied:
, and the following conditions are satisfied:
(i) ;
;
(ii)the set  -
-
 fulfills the weak domination property for all
fulfills the weak domination property for all  ;
;
(iii)there exist  and
and  such that
such that  is a weakly maximal solution of
is a weakly maximal solution of  .
.
Then  is a weakly minimal solution of
is a weakly minimal solution of  .
.
Proof.
It follows from Proposition 3.12 that

for all  Then,
Then,

It follows from  that there exists
that there exists  such that
such that  . So
. So  . Then, from (4.5) and (4.42), we get
. Then, from (4.5) and (4.42), we get

We now show that  is a weakly minimal solution of
is a weakly minimal solution of  . Assume that
. Assume that  is not a weakly minimal solution of
is not a weakly minimal solution of  . Then there exists
. Then there exists  such that
such that  . It follows from
. It follows from  that
that  , which contradicts (4.43). Thus
, which contradicts (4.43). Thus  is a weakly minimal solution of
is a weakly minimal solution of  and the proof is complete.
and the proof is complete.
Theorem 4.10 (converse duality).
Suppose that  ,
,  , and the following conditions are satisfied:
, and the following conditions are satisfied:
(i) ;
;
(ii)the set  -
-
 fulfills the weak domination property for all
fulfills the weak domination property for all  ;
;
(iii)there exist  and
and  such that
such that  is a weakly maximal solution of
is a weakly maximal solution of  .
.
Then  is a weakly minimal solution of
is a weakly minimal solution of  .
.
Proof.
By the similar proof method for Theorem 4.9, it follows from Proposition 3.14 that the conclusion holds.
5. Higher-Order Wolfe Type Duality
In this section, we introduce a kind of higher-order Wolf type dual problem for a constrained set-valued optimization problem by virtue of the higher-order weakly generalized adjacent epiderivative and discuss its weak duality, strong duality and converse duality properties.
Suppose that  ,
,  ,
,  , and
, and  ?
?  . We introduce a higher-order Wolfe type dual problem
. We introduce a higher-order Wolfe type dual problem of
of  as follows:
as follows:



A point 
 satisfying (5.1)–(5.3) is called a feasible solution of
satisfying (5.1)–(5.3) is called a feasible solution of  . A feasible solution
. A feasible solution 
 is called an optimal solution of
is called an optimal solution of  if, for any feasible solution
if, for any feasible solution  ,
,  .
.
Theorem 5.1 (weak duality).
Let  ,
,  ,
,  . Let the set
. Let the set  -
-

 fulfill the weak domination property for all
fulfill the weak domination property for all  . If
. If  is a feasible solution of
is a feasible solution of  and
and  is a feasible solution of
is a feasible solution of  , then
, then

Proof.
It follows from Proposition 3.12 that

Since  is a feasible solution of
is a feasible solution of  ,
,  . Take
. Take  . Then it follows from (5.3) that
. Then it follows from (5.3) that

From (5.1)–(5.6), we get

and the proof is complete.
Theorem 5.2 (weak duality).
Let  ,
,  , and
, and 
 and the set
and the set  -
-

 fulfill the weak domination property for all
fulfill the weak domination property for all  . Suppose that
. Suppose that  is
is  -convex like on a nonempty convext subset
-convex like on a nonempty convext subset  . If
. If  is a feasible solution of
is a feasible solution of  and
and  is a feasible solution of
is a feasible solution of  , then
, then

Proof.
By using similar proof method of Theorem 5.1 and Proposition 3.14, we have that the conclusion holds.
Theorem 5.3 (strong duality).
If the assumptions in Theorem 4.7 are satisfied and  , then there exist
, then there exist  and
and  such that
such that  is an optimal solution of
is an optimal solution of  .
.
Proof.
It follows from the proof of Theorem 4.7 that there exist  and
and  such that
such that  is a feasible solution of
is a feasible solution of  and
and  .
.
We now prove that  is an optimal solution of
is an optimal solution of  .
.
Suppose that  is not an optimal solution of
is not an optimal solution of  . Then there exists a feasible solution
. Then there exists a feasible solution  such that
such that

Therefore, it follows from  that
that

Since  is a weakly minimal solution of
is a weakly minimal solution of  , it follows from Theorem 5.2 that
, it follows from Theorem 5.2 that  . From (5.10), we get
. From (5.10), we get  , this is impossible since
, this is impossible since  . So
. So  is an optimal solution of
is an optimal solution of  .
.
By using similar proof methods for Theorems 4.9 and 4.10, we get the following results.
Theorem 5.4 (converse duality).
Suppose that there exists a  such that
such that  is an optimal solution of
is an optimal solution of  and
and  . Moreover, the assumptions
. Moreover, the assumptions  and
and  in Theorem 4.9 are satisfied. Then
in Theorem 4.9 are satisfied. Then  is a weakly minimal solution of
is a weakly minimal solution of  .
.
Theorem 5.5 (converse duality).
Suppose that there exists a  such that
such that  is an optimal solution of
is an optimal solution of  and
and  . Moreover, the assumptions
. Moreover, the assumptions  and
and  in Theorem 4.10 are satisfied. Then
in Theorem 4.10 are satisfied. Then  is a weakly minimal solution of
is a weakly minimal solution of  .
.
References
Jahn J, Rauh R: Contingent epiderivatives and set-valued optimization. Mathematical Methods of Operations Research 1997,46(2):193–211. 10.1007/BF01217690
Chen GY, Jahn J: Optimality conditions for set-valued optimization problems. Mathematical Methods of Operations Research 1998,48(2):187–200. 10.1007/s001860050021
Lalitha CS, Arora R: Weak Clarke epiderivative in set-valued optimization. Journal of Mathematical Analysis and Applications 2008,342(1):704–714. 10.1016/j.jmaa.2007.11.057
Aubin J-P, Frankowska H: Set-Valued Analysis, Systems & Control: Foundations & Applications. Volume 2. Birkhäuser, Boston, Mass, USA; 1990:xx+461.
Sach PH, Craven BD: Invex multifunctions and duality. Numerical Functional Analysis and Optimization 1991,12(5–6):575–591. 10.1080/01630569108816453
Aubin J-P, Ekeland I: Applied Nonlinear Analysis, Pure and Applied Mathematics. John Wiley & Sons, New York, NY, USA; 1984:xi+518.
Sach PH, Yen ND, Craven BD: Generalized invexity and duality theories with multifunctions. Numerical Functional Analysis and Optimization 1994,15(1–2):131–153. 10.1080/01630569408816555
Aubin J-P: Contingent derivatives of set-valued maps and existence of solutions to nonlinear inclusions and differential inclusions. In Mathematical Analysis and Applications, Part A, Advances in Mathematics. Supplementary Studies. Volume 7. Edited by: Nachbin L. Academic Press, New York, NY, USA; 1981:159–229.
Penot J-P: Differentiability of relations and differential stability of perturbed optimization problems. SIAM Journal on Control and Optimization 1984,22(4):529–551. 10.1137/0322033
Ioffe AD: Calculus of dini subdifferentials of functions and contingent coderivatives of set-valued maps. Nonlinear Analysis: Theory, Methods & Applications 1984,8(5):517–539. 10.1016/0362-546X(84)90091-9
Liu Z-B, Kim JK, Huang N-J: Existence of solutions for nonconvex and nonsmooth vector optimization problems. Journal of Inequalities and Applications 2008, 2008:-7.
Shi DS: Contingent derivative of the perturbation map in multiobjective optimization. Journal of Optimization Theory and Applications 1991,70(2):385–396. 10.1007/BF00940634
Yang XQ: Directional derivatives for set-valued mappings and applications. Mathematical Methods of Operations Research 1998,48(2):273–285. 10.1007/s001860050028
Gong X-H, Dong H-B, Wang S-Y: Optimality conditions for proper efficient solutions of vector set-valued optimization. Journal of Mathematical Analysis and Applications 2003,284(1):332–350. 10.1016/S0022-247X(03)00360-3
Taa A: Set-valued derivatives of multifunctions and optimality conditions. Numerical Functional Analysis and Optimization 1998,19(1–2):121–140. 10.1080/01630569808816819
Jiménez B, Novo V: Second order necessary conditions in set constrained differentiable vector optimization. Mathematical Methods of Operations Research 2003,58(2):299–317. 10.1007/s001860300283
Jahn J, Khan AA, Zeilinger P: Second-order optimality conditions in set optimization. Journal of Optimization Theory and Applications 2005,125(2):331–347. 10.1007/s10957-004-1841-0
Li SJ, Teo KL, Yang XQ: Higher-order optimality conditions for set-valued optimization. Journal of Optimization Theory and Applications 2008,137(3):533–553. 10.1007/s10957-007-9345-3
Li SJ, Teo KL, Yang XQ: Higher-order Mond-Weir duality for set-valued optimization. Journal of Computational and Applied Mathematics 2008,217(2):339–349. 10.1016/j.cam.2007.02.011
Li SJ, Chen CR: Higher order optimality conditions for Henig efficient solutions in set-valued optimization. Journal of Mathematical Analysis and Applications 2006,323(2):1184–1200. 10.1016/j.jmaa.2005.11.035
Luc DT: Theory of Vector Optimization, Lecture Notes in Economics and Mathematical Systems. Volume 319. Springer, Berlin, Germany; 1989:viii+173.
Acknowledgments
The authors thank anonymous referees for their valuable comments and suggestions, which helped them to improve the paper. This research was partially supported by the National Natural Science Foundation of China (10871216), Natural Science Foundation Project of CQ CSTC(2008BB0346) and the Excellent Young Teachers Program (2008EYT-016) of Chongqing Jiaotong University, China.
Author information
Authors and Affiliations
Corresponding author
Additional information
An erratum to this article is available at http://dx.doi.org/10.1155/2011/817965.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, Q.L., Li, S.J. Higher-Order Weakly Generalized Adjacent Epiderivatives and Applications to Duality of Set-Valued Optimization. J Inequal Appl 2009, 462637 (2009). https://doi.org/10.1155/2009/462637
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/462637