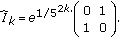- Research Article
- Open access
- Published:
A New Singular Impulsive Delay Differential Inequality and Its Application
Journal of Inequalities and Applications volume 2009, Article number: 461757 (2009)
Abstract
A new singular impulsive delay differential inequality is established. Using this inequality, the invariant and attracting sets for impulsive neutral neural networks with delays are obtained. Our results can extend and improve earlier publications.
1. Introduction
It is well known that inequality technique is an important tool for investigating dynamical behavior of differential equation. The significance of differential and integral inequalities in the qualitative investigation of various classes of functional equations has been fully illustrated during the last 40 years [1–3]. Various inequalities have been established such as the delay integral inequality in [4], the differential inequalities in [5, 6], the impulsive differential inequalities in [7–10], Halanay inequalities in [11–13], and generalized Halanay inequalities in [14–17]. By using the technique of inequality, the invariant and attracting sets for differential systems have been studied by many authors [9, 18–21].
However, the inequalities mentioned above are ineffective for studying the invariant and attracting sets of impulsive nonautonomous neutral neural networks with time-varying delays. On the basis of this, this article is devoted to the discussion of this problem.
Motivated by the above discussions, in this paper, a new singular impulsive delay differential inequality is established. Applying this equality and using the methods in [10, 22], some sufficient conditions ensuring the invariant set and the global attracting set for a class of neutral neural networks system with impulsive effects are obtained.
2. Preliminaries
Throughout the paper,  means
means  -dimensional unit matrix,
-dimensional unit matrix,  the set of real numbers,
the set of real numbers,  the set of positive integers, and
the set of positive integers, and  .
.  means that each pair of corresponding elements of
means that each pair of corresponding elements of  and
and  satisfies the inequality "
satisfies the inequality " (
( )". Especially,
)". Especially,  is called a nonnegative matrix if
is called a nonnegative matrix if  .
.

denotes the space of continuous mappings from the topological space  to the topological space
to the topological space  . In particular, let
. In particular, let  , where
, where  is a constant.
is a constant.

denotes the space of piecewise continuous functions  with at most countable discontinuous points and at this points
with at most countable discontinuous points and at this points  are right continuous. Especially, let
are right continuous. Especially, let  . Furthermore, put
. Furthermore, put  .
.

, where  denotes the derivative of
denotes the derivative of  . In particular, let
. In particular, let  .
.

is a positive integrable function and satisfies  and
and  .
.
For  ,
,  or
or  , we define
, we define  And we introduce the following norm, respectively,
And we introduce the following norm, respectively,

For any  , we define the following norm:
, we define the following norm:

For an  -matrix
-matrix  defined in [23], we denote
defined in [23], we denote

It is a cone without conical surface in  . We call it an "
. We call it an " -cone".
-cone".
3. Singular Impulsive Delay Differential Inequality
For convenience, we introduce the following conditions.
Let the  -dimensional diagonal matrix
-dimensional diagonal matrix  satisfy
satisfy

Let  be an
be an  -matrix, where
-matrix, where  and
and  satisfies
satisfies

Theorem 3.1.
Assume the conditions  and
and  hold. Let
hold. Let  and
and  be a solution of the following singular delay differential inequality with the initial conditions
be a solution of the following singular delay differential inequality with the initial conditions  :
:

where  , and
, and  ,
,  ,
,  . Then
. Then

provided that the initial conditions satisfy

where  ,
,  and the positive number
and the positive number  satisfies the following inequality:
satisfies the following inequality:

Proof.
By the conditions ( ) and the definition of
) and the definition of  -matrix, there is a constant vector
-matrix, there is a constant vector  such that
such that  ,
,  exists and
exists and  .
.
By using continuity, we obtain that there must exist a positive constant  satisfying the inequality (3.6), that is,
satisfying the inequality (3.6), that is,

Denote by

It follows from (3.3) and (3.5) that

In the following, we will prove that for any positive constant  ,
,

Let

If inequality (3.10) is not true, then  is a nonempty set and there must exist some integer
is a nonempty set and there must exist some integer  such that
such that  .
.
If  , by
, by  and the inequality (3.5), we can get
and the inequality (3.5), we can get


By using  , (3.3), (3.7), (3.12), (3.13), and
, (3.3), (3.7), (3.12), (3.13), and  , we obtain that
, we obtain that

Since  , we have
, we have  by
by  . Then (3.14) becomes
. Then (3.14) becomes

which contradicts the second inequality in (3.12).
If  , then
, then  by
by  and
and  . From the inequality (3.5), we can get
. From the inequality (3.5), we can get

By using  , (3.3), (3.7), (3.16), and
, (3.3), (3.7), (3.16), and  , we obtain that
, we obtain that

This is a contradiction. Thus the inequality (3.10) holds. Therefore, letting  in (3.10), we have
in (3.10), we have

The proof is complete.
Remark 3.2.
In order to overcome the difficulty that  in (3.3) may be discontinuous, we introduce the notation
in (3.3) may be discontinuous, we introduce the notation  which is different from the notation
which is different from the notation  in [7]. However, when
in [7]. However, when  is continuous in
is continuous in  , we have
, we have

So we can get [7, Lemma 1] when we choose  ,
,  ,
,  in Theorem 3.1.
in Theorem 3.1.
Remark 3.3.
Suppose that  and
and  in Theorem 3.1, then we can get [10, Theorem 3.1].
in Theorem 3.1, then we can get [10, Theorem 3.1].
4. Applications
The singular impulsive delay differential inequality obtained in Section 3 can be widely applied to study the dynamics of impulsive neutral differential equations. To illustrate the theory, we consider the following nonautonomous impulsive neutral neural networks with delays

where  is the neural state vector;
is the neural state vector;  ,
,  ,
,  are the interconnection matrices representing the weighting coefficients of the neurons;
are the interconnection matrices representing the weighting coefficients of the neurons;  are activation functions;
are activation functions;  are transmission delays;
are transmission delays;  denotes the external inputs at time
denotes the external inputs at time  .
.  represents impulsive perturbations; the fixed moments of time
represents impulsive perturbations; the fixed moments of time  satisfy
satisfy  .
.
The initial condition for (4.1) is given by

We always assume that for any  , (4.1) has at least one solution through (
, (4.1) has at least one solution through ( ), denoted by
), denoted by  or
or  (simply
(simply  or
or  if no confusion should occur).
if no confusion should occur).
Definition 4.1.
The set  is called a positive invariant set of (4.1), if for any initial value
is called a positive invariant set of (4.1), if for any initial value  , we have the solution
, we have the solution  for
for  .
.
Definition 4.2.
The set  is called a global attracting set of (4.1), if for any initial value
is called a global attracting set of (4.1), if for any initial value  , the solution
, the solution  converges to
converges to  as
as  . That is,
. That is,

where  ,
,  for
for  .
.
Throughout this section, we suppose the following.

 are continuous. Moreover,
are continuous. Moreover,  and
and  .
.
There exist nonnegative matrices  ,
,  ,
,  ,
,  and a constant
and a constant  such that
such that

There exist nonnegative matrices  such that
such that

There exist nonnegative matrices  ,
,  ,
,  such that for all
such that for all  the activating functions
the activating functions  and
and  satisfy
satisfy

There exists nonnegative matrix  , such that for all
, such that for all  ,
,  and
and 

.
Denote by

and let  be an
be an  -matrix, and
-matrix, and  .
.
There exists a constant  such that
such that

where  , and the scalar
, and the scalar  is determined by the inequality
is determined by the inequality

where  , and
, and

Theorem 4.3.
Assume that  hold. Then
hold. Then  is a global attracting set of (4.1).
is a global attracting set of (4.1).
Proof.
Denote  . Let
. Let  be the sign function. For
be the sign function. For  , define
, define 
Calculating the upper right derivative  along system (4.1). From (4.1),
along system (4.1). From (4.1),  and
and  we have
we have

On the other hand, from (4.1) and  , we have
, we have

Let

then from (4.12)–(4.14) and  , we have
, we have

By the conditions  and the definition of
and the definition of  -matrix, we may choose a vector
-matrix, we may choose a vector  such that
such that

By using continuity, we obtain that there must be a positive constant  satisfying the inequality (4.10). Let
satisfying the inequality (4.10). Let  and
and  , then
, then  . Since
. Since  , denote
, denote

then  . From the property of
. From the property of  -cone, we have,
-cone, we have,  .
.
For the initial conditions  ,
,  , where
, where  and
and  (no loss of generality, we assume
(no loss of generality, we assume  , and
, and  , we can get
, we can get

Then (4.18) yield

Let  ,
,  and
and  . Thus, all conditions of Theorem 3.1 are satisfied. By Theorem 3.1, we have
. Thus, all conditions of Theorem 3.1 are satisfied. By Theorem 3.1, we have

Suppose that for all  , the inequalities
, the inequalities

hold, where  .
.
From (4.21),  , and
, and  , we can get
, we can get

Since  , we have
, we have

On the other hand, it follows from  that
that

Then from (4.21)–(4.24), we have

which together with (4.22) yields that

Then, it follows from (4.21) and (4.26) that

Using Theorem 3.1 again, we have

By mathematical induction, we can conclude that

Noticing that  , by
, by  , we can use (4.29) to conclude that
, we can use (4.29) to conclude that

This implies that the conclusion of the theorem holds.
By using Theorem 4.3 with  , we can obtain a positive invariant set of (4.1), and the proof is similar to that of Theorem 4.3.
, we can obtain a positive invariant set of (4.1), and the proof is similar to that of Theorem 4.3.
Theorem 4.4.
Assume that  with
with  hold. Then
hold. Then  is a positive invariant set and also a global attracting set of (4.1).
is a positive invariant set and also a global attracting set of (4.1).
Remark 4.5.
Suppose that  in
in  , and
, and  , then we can get Theorems 1 and 2 in [9].
, then we can get Theorems 1 and 2 in [9].
Remark 4.6.
If  then (4.1) becomes the nonautonomous neutral neural networks without impulses, we can get Theorem 4.1 in [22].
then (4.1) becomes the nonautonomous neutral neural networks without impulses, we can get Theorem 4.1 in [22].
5. Illustrative Example
The following illustrative example will demonstrate the effectiveness of our results.
Example 5.1.
Consider nonlinear impulsive neutral neural networks:

with

where  ,
,  ,
,  ,
,  .
.
The parameters of conditions  are as follows:
are as follows:

It is easy to prove that  is an
is an  -matrix and
-matrix and

Let  , then
, then  and
and  . Let
. Let  which satisfies the inequality
which satisfies the inequality

Now, we discuss the asymptotical behavior of the system (5.1) as follows.
-
(i)
If
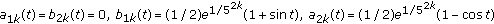 , then
, then 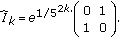 (5.6)
(5.6)
Thus  ,
,  ,
,  , and
, and  . Clearly, all conditions of Theorem 4.3 are satisfied, by Theorem 4.3,
. Clearly, all conditions of Theorem 4.3 are satisfied, by Theorem 4.3,  is a global attracting set of (5.1).
is a global attracting set of (5.1).
(ii)If  , then
, then  . By Theorem 4.4,
. By Theorem 4.4,  is a positive invariant set of (5.1).
is a positive invariant set of (5.1).
References
Walter W: Differential and Integral Inequalities. Springer, New York, NY, USA; 1970:x+352.
Lakshmikantham V, Leela S: Differential and Integral Inequalities: Theory and Applications. Vol. I: Ordinary Differential Equations, Mathematics in Science and Engineering. Volume 55. Academic Press, New York, NY, USA; 1969:ix+390.
Lakshmikantham V, Leela S: Differential and Integral Inequalities: Theory and Applications. Vol. II: Functional, Partial, Abstract, and Complex Differential Equations, Mathematics in Science and Engineering. Volume 55. Academic Press, New York, NY, USA; 1969:ix+319.
Xu DY: Integro-differential equations and delay integral inequalities. Tohoku Mathematical Journal 1992,44(3):365–378. 10.2748/tmj/1178227303
Wang L, Xu DY: Global exponential stability of Hopfield reaction-diffusion neural networks with time-varying delays. Science in China. Series F 2003,46(6):466–474. 10.1360/02yf0146
Huang YM, Xu DY, Yang ZG: Dissipativity and periodic attractor for non-autonomous neural networks with time-varying delays. Neurocomputing 2007,70(16–18):2953–2958.
Xu DY, Yang Z: Impulsive delay differential inequality and stability of neural networks. Journal of Mathematical Analysis and Applications 2005,305(1):107–120. 10.1016/j.jmaa.2004.10.040
Xu DY, Zhu W, Long S: Global exponential stability of impulsive integro-differential equation. Nonlinear Analysis: Theory, Methods & Applications 2006,64(12):2805–2816. 10.1016/j.na.2005.09.020
Xu DY, Yang Z: Attracting and invariant sets for a class of impulsive functional differential equations. Journal of Mathematical Analysis and Applications 2007,329(2):1036–1044. 10.1016/j.jmaa.2006.05.072
Xu DY, Yang Z, Yang Z: Exponential stability of nonlinear impulsive neutral differential equations with delays. Nonlinear Analysis: Theory, Methods & Applications 2007,67(5):1426–1439. 10.1016/j.na.2006.07.043
Driver RD: Ordinary and Delay Differential Equations, Applied Mathematical Sciences. Volume 20. Springer, New York, NY, USA; 1977:ix+501.
Gopalsamy K: Stability and Oscillations in Delay Differential Equations of Population Dynamics, Mathematics and Its Applications. Volume 74. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1992:xii+501.
Halanay A: Differential Equations: Stability, Oscillations, Time Lags. Academic Press, New York, NY, USA; 1966:xii+528.
Amemiya T: Delay-independent stabilization of linear systems. International Journal of Control 1983,37(5):1071–1079. 10.1080/00207178308933029
Liz E, Trofimchuk S: Existence and stability of almost periodic solutions for quasilinear delay systems and the Halanay inequality. Journal of Mathematical Analysis and Applications 2000,248(2):625–644. 10.1006/jmaa.2000.6947
Ivanov A, Liz E, Trofimchuk S: Halanay inequality, Yorke 3/2 stability criterion, and differential equations with maxima. Tohoku Mathematical Journal 2002,54(2):277–295. 10.2748/tmj/1113247567
Tian H: The exponential asymptotic stability of singularly perturbed delay differential equations with a bounded lag. Journal of Mathematical Analysis and Applications 2002,270(1):143–149. 10.1016/S0022-247X(02)00056-2
Lu KN, Xu DY, Yang ZC: Global attraction and stability for Cohen-Grossberg neural networks with delays. Neural Networks 2006,19(10):1538–1549. 10.1016/j.neunet.2006.07.006
Xu DY, Li S, Zhou X, Pu Z: Invariant set and stable region of a class of partial differential equations with time delays. Nonlinear Analysis: Real World Applications 2001,2(2):161–169. 10.1016/S0362-546X(00)00111-5
Xu DY, Zhao H-Y: Invariant and attracting sets of Hopfield neural networks with delay. International Journal of Systems Science 2001,32(7):863–866.
Zhao H: Invariant set and attractor of nonautonomous functional differential systems. Journal of Mathematical Analysis and Applications 2003,282(2):437–443. 10.1016/S0022-247X(02)00370-0
Guo Q, Wang X, Ma Z: Dissipativity of non-autonomous neutral neural networks with time-varying delays. Far East Journal of Mathematical Sciences 2008,29(1):89–100.
Berman A, Plemmons RJ: Nonnegative Matrices in the Mathematical Sciences, Computer Science and Applied Mathematic. Academic Press, New York, NY, USA; 1979:xviii+316.
Acknowledgments
This work was supported by the National Natural Science Foundation of China under Grant no. 10671133 and the Scientific Research Fund of Sichuan Provincial Education Department (08ZA044).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ma, Z., Wang, X. A New Singular Impulsive Delay Differential Inequality and Its Application. J Inequal Appl 2009, 461757 (2009). https://doi.org/10.1155/2009/461757
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/461757
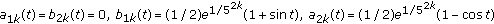 , then
, then