- Research Article
- Open access
- Published:
On Double Statistical 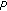 -Convergence of Fuzzy Numbers
-Convergence of Fuzzy Numbers
Journal of Inequalities and Applications volume 2009, Article number: 423792 (2009)
Abstract
Savas and Mursaleen defined the notions of statistically convergent and statistically Cauchy for double sequences of fuzzy numbers. In this paper, we continue the study of statistical convergence by proving some theorems.
1. Introduction
For sequences of fuzzy numbers, Nanda [1] studied the sequences of fuzzy numbers and showed that the set of all convergent sequences of fuzzy numbers forms a complete metric space. Kwon [2] introduced the definition of strongly p-Cesàro summability of sequences of fuzzy numbers. Savas [3] introduced and discussed double convergent sequences of fuzzy numbers and showed that the set of all double convergent sequences of fuzzy numbers is complete. Savas [4] studied some equivalent alternative conditions for a sequence of fuzzy numbers to be statistically Cauchy and he continue to study in [5, 6]. Recently Mursaleen and Basarir [7] introduced and studied some new sequence spaces of fuzzy numbers generated by nonnegative regular matrix. Quite recently, Savas and Mursaleen [8] defined statistically convergent and statistically Cauchy for double sequences of fuzzy numbers. In this paper, we continue the study of double statistical convergence and introduce the definition of double strongly  -Cesàro summabilty of sequences of fuzzy numbers.
-Cesàro summabilty of sequences of fuzzy numbers.
2. Definitions and Preliminary Results
Since the theory of fuzzy numbers has been widely studied, it is impossible to find either a commonly accepted definition or a fixed notation. We therefore being by introducing some notations and definitions which will be used throughout.
Let  . The spaces
. The spaces  has a linear structure induced by the operations
has a linear structure induced by the operations

for  and
and  . The Hausdorff distance between
. The Hausdorff distance between  and
and  of
of  is defined as
is defined as

It is well known that  is a complete (not separable) metric space.
is a complete (not separable) metric space.
A fuzzy number is a function  from
from  to
to  satisfying
satisfying
(1) is normal, that is, there exists an
is normal, that is, there exists an  such that
such that  ;
;
(2) is fuzzy convex, that is, for any
is fuzzy convex, that is, for any  and
and  ,
,

(3) is upper semicontinuous;
is upper semicontinuous;
(4)the closure of  ; denoted by
; denoted by  , is compact.
, is compact.
These properties imply that for each  , the
, the  -level set
-level set

is a nonempty compact convex, subset of  , as is the support
, as is the support  . Let
. Let  denote the set of all fuzzy numbers. The linear structure of
denote the set of all fuzzy numbers. The linear structure of  induces the addition
induces the addition  and scalar multiplication
and scalar multiplication  ,
,  , in terms of
, in terms of  -level sets, by
-level sets, by

for each  .
.
Define for each  ,
,

and  clearly
clearly  with
with  if
if  . Moreover
. Moreover  is a complete, separable, and locally compact metric space [9].
is a complete, separable, and locally compact metric space [9].
Throughout this paper,  will denote
will denote  with
with  . We will need the following definitions (see [8]).
. We will need the following definitions (see [8]).
Definition 2.1.
A double sequence  of fuzzy numbers is said to be convergent in Pringsheim's sense or
of fuzzy numbers is said to be convergent in Pringsheim's sense or  -convergent to a fuzzy number
-convergent to a fuzzy number  , if for every
, if for every  there exists
there exists  such that
such that

and we denote by  . The number
. The number  is called the Pringsheim limit of
is called the Pringsheim limit of  .
.
More exactly we say that a double sequence  converges to a finite number
converges to a finite number  if
if  tend to
tend to  as both
as both  and
and  tend to
tend to  independently of one another.
independently of one another.
Let  denote the set of all double convergent sequences of fuzzy numbers.
denote the set of all double convergent sequences of fuzzy numbers.
Definition 2.2.
A double sequence  of fuzzy numbers is said to be
of fuzzy numbers is said to be  -Cauchy sequence if for every
-Cauchy sequence if for every  there exists
there exists  such that
such that

Let  denote the set of all double Cauchy sequences of fuzzy numbers.
denote the set of all double Cauchy sequences of fuzzy numbers.
Definition 2.3.
A double sequence  of fuzzy numbers is bounded if there exists a positive number
of fuzzy numbers is bounded if there exists a positive number  such that
such that  for all
for all  and
and  ,
,

We will denote the set of all bounded double sequences by  .
.
Let  be a two-dimensional set of positive integers and let
be a two-dimensional set of positive integers and let  be the numbers of
be the numbers of  in
in  such that
such that  and
and  . Then the lower asymptotic density of
. Then the lower asymptotic density of  is defined as
is defined as

In the case when the sequence  has a limit, then we say that
has a limit, then we say that  has a natural density and is defined as
has a natural density and is defined as

For example, let  , where
, where  is the set of natural numbers. Then
is the set of natural numbers. Then

(i.e., the set  has double natural density zero).
has double natural density zero).
Definition 2.4.
A double sequence  of fuzzy numbers is said to be statistically convergent to
of fuzzy numbers is said to be statistically convergent to  provided that for each
provided that for each  ,
,

In this case we write  and we denote the set of all double statistically convergent sequences of fuzzy numbers by
and we denote the set of all double statistically convergent sequences of fuzzy numbers by  .
.
Definition 2.5.
A double sequence  of fuzzy numbers is said to be statistically
of fuzzy numbers is said to be statistically  -Cauchy if for every
-Cauchy if for every  there exist
there exist  and
and  such that
such that

That is,  , a.a.(
, a.a.( ).
).
Let  denote the set of all double Cauchy sequences of fuzzy numbers.
denote the set of all double Cauchy sequences of fuzzy numbers.
Definition 2.6.
A double sequence  of fuzzy and let
of fuzzy and let  be a positive real numbers. The sequence
be a positive real numbers. The sequence  is said to be strongly double
is said to be strongly double  -Cesaro summable if there is a fuzzy number
-Cesaro summable if there is a fuzzy number  such that
such that

In which case we say that  is strongly
is strongly  -Cesaro summable to
-Cesaro summable to  .
.
It is quite clear that if a sequence  is statistically
is statistically  -convergent, then it is a statistically
-convergent, then it is a statistically  -Cauchy sequence [8]. It is also easy to see that if there is a convergent sequence
-Cauchy sequence [8]. It is also easy to see that if there is a convergent sequence  such that
such that  a.a.(
a.a.( ), then
), then  is statistically convergent.
is statistically convergent.
3. Main Result
Theorem 3.1.
A double sequence  of fuzzy numbers is statistically
of fuzzy numbers is statistically  -Cauchy then there is a
-Cauchy then there is a  -convergent double sequence
-convergent double sequence  such that
such that  a.a.(
a.a.( ).
).
Proof.
Let us begin with the assumption that  is statistically
is statistically  -Cauchy this grant us a closed ball
-Cauchy this grant us a closed ball  that contains
that contains  a.a.(
a.a.( ) for some positive numbers
) for some positive numbers  and
and  . Clearly we can choose
. Clearly we can choose  and
and  such that
such that  contains
contains  a.a.(
a.a.( ). It is also clear that
). It is also clear that  a.a.(
a.a.( ); for
); for

we have

Thus  is a closed ball of diameter less than or equal to 1 that contains
is a closed ball of diameter less than or equal to 1 that contains  a.a.(
a.a.( ). Now we let us consider the second stage to this end we choose
). Now we let us consider the second stage to this end we choose  and
and  such that
such that  In a manner similar to the first stage we have
In a manner similar to the first stage we have  , a.a.(
, a.a.( ). Note the diameter of
). Note the diameter of  is less than or equal
is less than or equal  . If we now consider the (
. If we now consider the ( )th general stage we obtain the following. First a sequence
)th general stage we obtain the following. First a sequence  of closed balls such that for each (
of closed balls such that for each ( ),
),  , the diameter of
, the diameter of  is not greater than
is not greater than  with
with  , a.a.(
, a.a.( ). By the nested closed set theorem of a complete metric space we have
). By the nested closed set theorem of a complete metric space we have  . So there exists a fuzzy number
. So there exists a fuzzy number  . Using the fact that
. Using the fact that  , a.a.(
, a.a.( ), we can choose an increasing sequence
), we can choose an increasing sequence  of positive integers such that
of positive integers such that

Now define a double subsequence  of
of  consisting of all terms
consisting of all terms  such that
such that  and if
and if

Next we define the sequence ( ) by
) by

Then  indeed if
indeed if  and
and  then either
then either  is a term of
is a term of  . Which means
. Which means  or
or  and
and  diameter of
diameter of  . We will now show that
. We will now show that  a.a.(
a.a.( ). Note that if
). Note that if  then
then

and by (3.3)

Hence the limit as  is 0 and
is 0 and  a.a.(
a.a.( ). This completes the proof.
). This completes the proof.
Theorem 3.2.
If  is strongly
is strongly  -Cesaro summable or statistically
-Cesaro summable or statistically  -convergent to
-convergent to  then there is a
then there is a  -convergent double sequences
-convergent double sequences  and a statistically
and a statistically  -null sequence
-null sequence  such that
such that  and
and  .
.
Proof.
Note that if  is strongly
is strongly  -Cesaro summable to
-Cesaro summable to  then
then  is statistically
is statistically  -convergent to
-convergent to  . Let
. Let  and
and  and select two increasing index sequences of positive integers
and select two increasing index sequences of positive integers  and
and  such that
such that  and
and  , we have
, we have

Define  and
and  as follows: if
as follows: if  and
and  , set
, set  and
and  . Suppose that
. Suppose that  and
and  ,
,  then
then

We now show that  . Let
. Let  be given, pick
be given, pick  be given, and pick
be given, and pick  and
and  such that
such that  , thus for
, thus for  , since
, since  if
if  and
and  if
if  we have
we have  .
.
Next we show that  is a statistically
is a statistically  -null double sequence, that is, we need to show that
-null double sequence, that is, we need to show that  . Let
. Let  if
if  such that
such that  then
then  for all
for all  . From the construction of
. From the construction of  , if
, if  and
and  then
then  only if
only if  . It follows that if
. It follows that if  and
and  then
then

Thus for  and
and  and
and  then
then

this completes the proof.
Corollary 3.3.
If  is a strongly
is a strongly  -Cesaro summable to
-Cesaro summable to  or statistically
or statistically  -convergent to
-convergent to  then
then  has a double subsequence which is
has a double subsequence which is  -converges to
-converges to  .
.
4. Conclusion
In recent years the statistical convergence has been adapted to the sequences of fuzzy numbers. Double statistical convergence of sequences of fuzzy numbers was first deduced in similar form by Savas and Mursaleen as we explain now: a double sequences  is said to be
is said to be  -statistically convergent to
-statistically convergent to  provided that for each
provided that for each  ,
,

Since the set of real numbers can be embedded in the set of fuzzy numbers, statistical convergence in reals can be considered as a special case of those fuzzy numbers. However, since the set of fuzzy numbers is partially ordered and does not carry a group structure, most of the results known for the sequences of real numbers may not be valid in fuzzy setting. Therefore, this theory should not be considered as a trivial extension of what has been known in real case. In this paper, we continue the study of double statistical convergence and also some important theorems are proved.
References
Nanda S: On sequences of fuzzy numbers. Fuzzy Sets and Systems 1989,33(1):123–126. 10.1016/0165-0114(89)90222-4
Kwon J-S: On statistical and -Cesaro convergence of fuzzy numbers. Journal of Applied Mathematics and Computing 2000,7(1):195–203.
Savas E: A note on double sequences of fuzzy numbers. Turkish Journal of Mathematics 1996,20(2):175–178.
Savas E: On statistically convergent sequences of fuzzy numbers. Information Sciences 2001,137(1–4):277–282.
Savas E: A note on sequence of fuzzy numbers. Information Sciences 2000,124(1–4):297–300.
Savas E: On lacunary statistically convergent double sequences of fuzzy numbers. Applied Mathematics Letters 2008,21(2):134–141. 10.1016/j.aml.2007.01.008
Mursaleen M, Basarir M: On some new sequence spaces of fuzzy numbers. Indian Journal of Pure and Applied Mathematics 2003,34(9):1351–1357.
Savas E, Mursaleen : On statistically convergent double sequences of fuzzy numbers. Information Sciences 2004,162(3–4):183–192. 10.1016/j.ins.2003.09.005
Diamond P, Kloeden P: Metric spaces of fuzzy sets. Fuzzy Sets and Systems 1990,35(2):241–249. 10.1016/0165-0114(90)90197-E
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Savas, E., Patterson, R.F. On Double Statistical 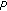 -Convergence of Fuzzy Numbers.
J Inequal Appl 2009, 423792 (2009). https://doi.org/10.1155/2009/423792
-Convergence of Fuzzy Numbers.
J Inequal Appl 2009, 423792 (2009). https://doi.org/10.1155/2009/423792
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/423792