- Research Article
- Open access
- Published:
Subnormal Solutions of Second-Order Nonhomogeneous Linear Differential Equations with Periodic Coefficients
Journal of Inequalities and Applications volume 2009, Article number: 416273 (2009)
Abstract
We obtain the representations of the subnormal solutions of nonhomogeneous linear differential equation  , where
, where  and
and  are polynomials in
are polynomials in  such that
such that  and
and  are not all constants,
are not all constants,  . We partly resolve the question raised by G. G. Gundersen and E. M. Steinbart in 1994.
. We partly resolve the question raised by G. G. Gundersen and E. M. Steinbart in 1994.
1. Introduction
We use the standard notations from Nevanlinna theory in this paper (see [1–3]).
The study of the properties of the solutions of a linear differential equation with periodic coefficients is one of the difficult aspects in the complex oscillation theory of differential equations. However, it is also one of the important aspects since it relates to many special functions. Some important researches were done by different authors; see, for instance, [4–9].
Now, we firstly consider the second-order homogeneous linear differential equations

where  and
and  are polynomials in
are polynomials in  and are not both constants. It is well known that every solution
and are not both constants. It is well known that every solution  of (1.1) is an entire function.
of (1.1) is an entire function.
Let  be an entire function. We define
be an entire function. We define

to be the  -type order of
-type order of  .
.
If  is a solution of (1.1) and if
is a solution of (1.1) and if  satisfies
satisfies  , then we say that
, then we say that  is a subnormal solution of (1.1). For convenience, we also say that
is a subnormal solution of (1.1). For convenience, we also say that  is a subnormal solution of (1.1).
is a subnormal solution of (1.1).
-
H.
Wittich has given the general forms of all subnormal solutions of (1.1) that are shown in the following theorem.
Theorem 1 A (see [9]).
If  is a subnormal solution of (1.1), where
is a subnormal solution of (1.1), where  and
and  are polynomials in
are polynomials in  and are not both constants, then
and are not both constants, then  must have the form
must have the form

where  is an integer and
is an integer and  are constants with
are constants with  .
.
-
G.
G. Gundersen and E. M. Steinbart refined Theorem A and obtained the exact forms of subnormal solutions of (1.1) as follows.
Theorem 1 B (see [6]).
In addition to the statement of Theorem A, the following statements hold with regard to the subnormal solutions  of (1.1).
of (1.1).
(i)If  and
and  then any subnormal solution
then any subnormal solution  of (1.1) must have the form
of (1.1) must have the form

where  is an integer and
is an integer and  are constants with
are constants with 
(ii)If  and
and  , then any subnormal solution
, then any subnormal solution  of (1.1) must be a constant.
of (1.1) must be a constant.
(iii)If  , then the only subnormal solution
, then the only subnormal solution  of (1.1) is
of (1.1) is  .
.
Whether the conclusions of Theorem A and Theorem B can be generalized or not, Gundersen and Steinbart considered the second-order nonhomogeneous linear differential equations

where  , and
, and  are polynomials in
are polynomials in  such that
such that  are not both constants. They found the exact forms of all subnormal solutions of (1.5), that is, what is mentioned in [6, Theorem ?2.2, Theorem ?2.3 and Theorem ?2.4].
are not both constants. They found the exact forms of all subnormal solutions of (1.5), that is, what is mentioned in [6, Theorem ?2.2, Theorem ?2.3 and Theorem ?2.4].
In [6], they also have raised the following problem, that is, what about the forms of the subnormal solutions of the equation

where  , and
, and  are polynomials in
are polynomials in  such that
such that  ,
,  ,
,  , and
, and  are not all constants?
are not all constants?
In [7], we have obtained the exact forms of all subnormal solutions of homogeneous equation

where  , and
, and  are polynomials in
are polynomials in  and are not all constants.
and are not all constants.
In this paper, we obtain the forms of subnormal solutions of nonhomogeneous linear differential equation (1.6) when  . We have the following theorem.
. We have the following theorem.
Theorem 1.1.
Suppose that  is a subnormal solution of (1.6), where
is a subnormal solution of (1.6), where  ,
,  , and
, and  are polynomials in
are polynomials in  such that
such that  and
and  are not all constants.
are not all constants.
(i)If  and
and  , then
, then  must have the form
must have the form

where  is a constant,
is a constant,  and
and  are polynomials in
are polynomials in  .
.
(ii)If  and
and  , then
, then  must have the form
must have the form

where  is a constant,
is a constant,  and
and  are constants that may or may not be equal to zero,
are constants that may or may not be equal to zero,  may be equal to zero or may be a polynomial in
may be equal to zero or may be a polynomial in  ,
,  , and
, and  are polynomials in
are polynomials in  with
with  .
.
2. Lemmas for the Proof
In order to prove Theorem 1.1, we need some lemmas.
Lemma 2.1 (see [7]).
Suppose that  is a subnormal solution of (1.7), where
is a subnormal solution of (1.7), where  ,
,  ,
,  and
and  are polynomials in
are polynomials in  and are not all constants.
and are not all constants.
(i)If  and
and  then any subnormal solution
then any subnormal solution  must be a constant.
must be a constant.
(ii)If  and
and  then
then  must have the form
must have the form

where  is a polynomial in
is a polynomial in  with
with  .
.
Lemma 2.2 (see [10]).
Let  be a transcendental meromorphic function, let
be a transcendental meromorphic function, let  be a given real constant, and let
be a given real constant, and let  . Then there exists a constant
. Then there exists a constant  such that the following two statements hold (where
such that the following two statements hold (where  ).
).
(i)There exists a set  that has linear measure zero such that if
that has linear measure zero such that if  , then there is a constant
, then there is a constant  such that for all
such that for all  satisfying
satisfying  and
and  one has
one has

(ii)There exists a set  that has finite logarithmic measure such that (2.2) holds for all
that has finite logarithmic measure such that (2.2) holds for all  satisfying
satisfying  .
.
Lemma 2.3 (see [6]).
Let  with
with  as
as  and let
and let  Let
Let

and set

Let  be analytic on the set
be analytic on the set  . Suppose that
. Suppose that  is unbounded on the set
is unbounded on the set  . Then there exists an infinite sequence of points
. Then there exists an infinite sequence of points  with
with  as
as  such that
such that

Lemma 2.4 (see [8]).
Consider the nth- order differential equation of the form

where  are polynomials in
are polynomials in  and
and  with
with  . Suppose that
. Suppose that  is an entire and subnormal solution of (2.6) and that
is an entire and subnormal solution of (2.6) and that  can be expressed as
can be expressed as  , where
, where  is a constant and
is a constant and  is analytic on
is analytic on  . Then
. Then  has the form
has the form

where  is a constant and
is a constant and  and
and  are polynomials in
are polynomials in  .
.
As an application of Lemma 2.4, one has the following lemma.
Lemma 2.5.
Suppose that  is an entire subnormal solution of (2.6), where
is an entire subnormal solution of (2.6), where  are polynomials in
are polynomials in  and
and  with
with  , and that
, and that  and
and  are linearly dependent. Then
are linearly dependent. Then  has the form
has the form

where  is a constant and
is a constant and  and
and  are polynomials in
are polynomials in  .
.
Proof.
Since  is entire and is linearly dependent with
is entire and is linearly dependent with  ,
,  can be written as
can be written as  (see [11, page 382]), where
(see [11, page 382]), where  is a constant and
is a constant and  is analytic on
is analytic on  . Then we have the representation from Lemma 2.4.
. Then we have the representation from Lemma 2.4.
Lemma 2.6.
Suppose that  is a solution of (1.6), where
is a solution of (1.6), where  ,
,  ,
,  ,
,  ,
,  , and
, and  are polynomials in
are polynomials in  such that
such that  ,
,  ,
,  and
and  are not all constants. If
are not all constants. If

then there exists a polynomial  such that
such that

where  is a solution of
is a solution of

where  and
and  are polynomials in
are polynomials in  with
with 
Proof.
Let  and set
and set

where  is the constant such that
is the constant such that

It follows from (1.6) and (2.12) that

where

So  and
and  are polynomials in
are polynomials in  and
and  , respectively, and
, respectively, and  by (2.13), but
by (2.13), but  and
and  have the exact representations that depend on the relations of
have the exact representations that depend on the relations of  , and
, and  . If
. If  , then (2.14) is of the form (2.11), and (2.12) gives (2.10). If
, then (2.14) is of the form (2.11), and (2.12) gives (2.10). If  , then we repeat the above process finite times until we obtain (2.10) and (2.11). This completes the proof of Lemma 2.6.
, then we repeat the above process finite times until we obtain (2.10) and (2.11). This completes the proof of Lemma 2.6.
3. Proof of Theorem
In this section, we will prove Theorem 1.1.
Proof.
-
(i)
Suppose that
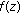 is a subnormal solution of (1.6) with
is a subnormal solution of (1.6) with  and
and  . If
. If 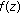 is a polynomial solution of (1.6), then
is a polynomial solution of (1.6), then  must be a constant, which is of the form (1.8). Thus we suppose that
must be a constant, which is of the form (1.8). Thus we suppose that  is transcendental. It follows from Lemma 2.2(i) that there exists a set
is transcendental. It follows from Lemma 2.2(i) that there exists a set  that has linear measure zero such that if
that has linear measure zero such that if  , then there is a constant
, then there is a constant 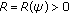 such that for all
such that for all  satisfying
satisfying 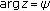 and
and 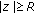 , we have
, we have 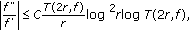 (3.1)
(3.1)
where  is a constant and
is a constant and  . It also follows from Lemma 2.2(ii) that there exists a set
. It also follows from Lemma 2.2(ii) that there exists a set  that has finite logarithmic measure such that (3.1) holds for all
that has finite logarithmic measure such that (3.1) holds for all  satisfying
satisfying  .
.
Now let  be an infinite sequence satisfying
be an infinite sequence satisfying  such that
such that  for all
for all  and
and  as
as  Let
Let  be a small constant such that
be a small constant such that  and
and  . Set
. Set

and set

From above, we have that (3.1) holds on the set 
We now assert that  is bounded on the set
is bounded on the set  . On the contrary, it follows from Lemma 2.3 that there exists a sequence of points
. On the contrary, it follows from Lemma 2.3 that there exists a sequence of points  with
with  as
as  such that
such that


By (1.6), we have for all  ,
,

It follows from (3.4)–(3.6) and  that (3.6) yields
that (3.6) yields  as
as  on the set
on the set  This is a contradiction.
This is a contradiction.
By the maximum modulus principle,  is bounded in the angular domain
is bounded in the angular domain

However, we know

where the integral of  is defined on the simple contour
is defined on the simple contour  , extending from a point
, extending from a point  to a point
to a point  in the complex domain.
in the complex domain.
So we obtain

as  in the angular domain
in the angular domain  .
.
Thus , from the Cauchy integral formula, we obtain

as  in the angular domain
in the angular domain  . By (1.6), (3.8), and (3.9), we have for some constant
. By (1.6), (3.8), and (3.9), we have for some constant 

as  in the angular domain
in the angular domain  . Together with (3.8) and (3.11),
. Together with (3.8) and (3.11),  is bounded in the angular domain
is bounded in the angular domain  .
.
If  , it follows from Lemma 2.5 that
, it follows from Lemma 2.5 that  must have the form (1.8).
must have the form (1.8).
If  , since
, since  is a subnormal solution of (1.6), so is
is a subnormal solution of (1.6), so is  . Thus,
. Thus,

will be a subnormal solution of (1.7). Since we suppose that  , we will discuss the following two cases.
, we will discuss the following two cases.
Case 1.
If  we have, by Lemma 2.1(i),
we have, by Lemma 2.1(i),

where  is a constant. Hence
is a constant. Hence  , that is,
, that is,

From this,  can be written as
can be written as  (see [11, page 382]), where
(see [11, page 382]), where  is a constant and
is a constant and  is analytic on
is analytic on  . Thus,
. Thus,  can be written as
can be written as  , where
, where  is a constant and
is a constant and  is analytic on
is analytic on  . It follows from Lemma 2.4 that
. It follows from Lemma 2.4 that

where  is a constant,
is a constant,  and
and  are polynomials in
are polynomials in  . Thus,
. Thus,  has the form of (1.8).
has the form of (1.8).
Case 2.
If  we obtain from Lemma 2.1(ii) that
we obtain from Lemma 2.1(ii) that

where  is a polynomial in
is a polynomial in  with
with  .
.
However, we can assert that  in (3.16). Otherwise, there exists
in (3.16). Otherwise, there exists  such that
such that

By (3.16), we have

Thus from (3.16) and (3.18), we have

By repeating this process finite times, we obtain that for any integer  ,
,

We have, by (3.17) and (3.20),

as  This is a contradiction to the fact that
This is a contradiction to the fact that  is bounded in the angular domain
is bounded in the angular domain  . This shows that
. This shows that  is not possible when
is not possible when  under the hypotheses. This completes the proof of part (i).
under the hypotheses. This completes the proof of part (i).
-
(ii)
We firstly suppose that
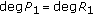 . Since
. Since 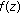 is a subnormal solution of (1.6), so is
is a subnormal solution of (1.6), so is 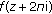 . Set
. Set 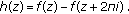 (3.22)
(3.22)
Then  is a subnormal solution of (1.7). Now if
is a subnormal solution of (1.7). Now if  , this shows that
, this shows that  and
and  has the form of (1.9) by Lemma 2.5. Thus, we suppose that
has the form of (1.9) by Lemma 2.5. Thus, we suppose that  in the following.
in the following.
Now, assume that  .
.
If  it follows from the proof of Case 1 of Theorem 1.1(i) that
it follows from the proof of Case 1 of Theorem 1.1(i) that  has the form of (1.9).
has the form of (1.9).
If  we obtain from Lemma 2.1(ii) that
we obtain from Lemma 2.1(ii) that

where  is a polynomial in
is a polynomial in  with
with  .
.
Set

where  is an integer and
is an integer and  are constants with
are constants with 
Let  and set
and set

where 
Now, we will discuss the following two cases.
Case A.
We consider  in (3.24). Let
in (3.24). Let  be a constant defined by
be a constant defined by

and set

Since  is a subnormal solution of (1.7), it follows from (3.27) that
is a subnormal solution of (1.7), it follows from (3.27) that  satisfies
satisfies

We obtain from (3.23)–(3.28) that

where  and
and  are polynomials in
are polynomials in  with
with 
Set

It follows from (1.6), (3.25), (3.29) and (3.30) that 
Set

So  , and
, and  satisfies
satisfies

We have by (3.27) that  is a subnormal solution of (1.7),
is a subnormal solution of (1.7),  is a subnormal solution of (3.29). Moreover,
is a subnormal solution of (3.29). Moreover,  is also a subnormal solution of (3.32) by (3.30) and
is also a subnormal solution of (3.32) by (3.30) and  is a subnormal solution of (1.6). Thus, we deduce from Theorem 1.1(i) and (3.32) with
is a subnormal solution of (1.6). Thus, we deduce from Theorem 1.1(i) and (3.32) with  that
that  has the form
has the form

where  is a constant,
is a constant,  and
and  are polynomials in
are polynomials in  . Hence (3.23), (3.24), (3.27), (3.30), and (3.33) yield
. Hence (3.23), (3.24), (3.27), (3.30), and (3.33) yield

where  and
and  are constants,
are constants,  , and
, and  are polynomials in
are polynomials in  with
with  . This is the form of (1.9).
. This is the form of (1.9).
Case B.
We consider  in (3.24). Let
in (3.24). Let  be a constant defined by
be a constant defined by

where  is a number such that
is a number such that  is the first coefficient
is the first coefficient  in (3.24) which is not equal to zero. Set
in (3.24) which is not equal to zero. Set

Similar to the proof of Case A of Theorem 1.1(ii), we have

where  and
and  are constants,
are constants,  and,
and,  are polynomials in
are polynomials in  with
with  . Set
. Set  . Then
. Then  is a polynomial in
is a polynomial in  by the hypotheses of
by the hypotheses of  in (3.36). This is the form of (1.9). We have proved Theorem 1.1(ii) when
in (3.36). This is the form of (1.9). We have proved Theorem 1.1(ii) when 
Now we suppose that  . By Lemma 2.6, there exists a polynomial
. By Lemma 2.6, there exists a polynomial  in
in  , satisfies (2.10) and (2.11).
, satisfies (2.10) and (2.11).
Since  and since we have proved Theorem 1.1 holds in the cases when
and since we have proved Theorem 1.1 holds in the cases when  holds, we can apply this result to (2.11).
holds, we can apply this result to (2.11).
If  , it follows from Theorem 1.1(i) that
, it follows from Theorem 1.1(i) that

where  is a constant,
is a constant,  and
and  are polynomials in
are polynomials in  . By (2.10) and (3.38), we obtain that
. By (2.10) and (3.38), we obtain that

where  is a constant,
is a constant,  and
and  are polynomials in
are polynomials in  . This is a form of (1.9).
. This is a form of (1.9).
If  , it follows from the proof of Theorem 1.1(ii) when
, it follows from the proof of Theorem 1.1(ii) when  that
that

where  and
and  are polynomials in
are polynomials in  with
with  ,
,  and
and  are constants that may or may not be equal to zero. By (2.10) and (3.40), we obtain that
are constants that may or may not be equal to zero. By (2.10) and (3.40), we obtain that  has the form of (1.9). Theorem 1.1(ii) is completed.
has the form of (1.9). Theorem 1.1(ii) is completed.
Now, we give some examples to show that Theorem 1.1 is correct.
Example 3.1.
Let  , then
, then  satisfies
satisfies

This is an example of Theorem 1.1(i).
Example 3.2.
Let  , then
, then  satisfies
satisfies

This is an example of Theorem 1.1(ii) with  and
and  .
.
Example 3.3.
Let  , then
, then  satisfies
satisfies

This is an example of Theorem 1.1 (ii) with  and
and  .
.
References
Gao SA, Chen ZX, Chen TW: Oscillation Theory of Linear Differential Equation. Huazhong University of Science and Technology Press; 1998.
Hayman WK: Meromorphic Functions, Oxford Mathematical Monographs. Clarendon Press, Oxford, UK; 1964:xiv+191.
Yang L: Value Distribution Theory and Its New Researches. Science Press, Beijing, China; 1992.
Chen ZX, Shon KH: On subnormal solutions of second order linear periodic differential equations. Science in China. Series A 2007,50(6):786–800. 10.1007/s11425-007-0050-3
Chen ZX, Gao SA, Shon KH: On the dependent property of solutions for higher order periodic differential equations. Acta Mathematica Scientia. Series B 2007,27(4):743–752. 10.1016/S0252-9602(07)60072-1
Gundersen GG, Steinbart EM: Subnormal solutions of second order linear differential equations with periodic coefficients. Results in Mathematics 1994,25(3–4):270–289.
Huang ZB, Chen ZX: Subnormal solutions of second order homogeneous linear differential equations with periodic coefficients. Acta Mathematica Sinica, Series A 2009,52(1):9–16.
Urabe H, Yang CC: On factorization of entire functions satisfying differential equations. Kodai Mathematical Journal 1991,14(1):123–133. 10.2996/kmj/1138039342
Wittich H: Subnormale Lösungen Differentialgleichung:
 Nagoya Mathematical Journal 1967, 30: 29–37.
Nagoya Mathematical Journal 1967, 30: 29–37.Gundersen GG: Estimates for the logarithmic derivative of a meromorphic function, plus similar estimates. Journal of the London Mathematical Society 1988,37(1):88–104.
Ince E: Ordinary Differential Equations. Dover, New York, NY, USA; 1926.
Acknowledgements
The authors are very grateful to the referee for his (her) many valuable comments and suggestions which greatly improved the presentation of this paper. The project was supposed by the National Natural Science Foundation of China (no. 10871076), and also partly supposed by the School of Mathematical Sciences Foundation of SCNU, China.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Huang, ZB., Chen, ZX. & Li, Q. Subnormal Solutions of Second-Order Nonhomogeneous Linear Differential Equations with Periodic Coefficients. J Inequal Appl 2009, 416273 (2009). https://doi.org/10.1155/2009/416273
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/416273
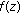 is a subnormal solution of (1.6) with
is a subnormal solution of (1.6) with  and
and  . If
. If 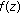 is a polynomial solution of (1.6), then
is a polynomial solution of (1.6), then  must be a constant, which is of the form (1.8). Thus we suppose that
must be a constant, which is of the form (1.8). Thus we suppose that  is transcendental. It follows from Lemma 2.2(i) that there exists a set
is transcendental. It follows from Lemma 2.2(i) that there exists a set  that has linear measure zero such that if
that has linear measure zero such that if  , then there is a constant
, then there is a constant 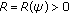 such that for all
such that for all  satisfying
satisfying 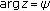 and
and 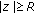 , we have
, we have 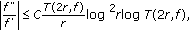
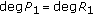 . Since
. Since 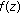 is a subnormal solution of (1.6), so is
is a subnormal solution of (1.6), so is 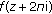 . Set
. Set 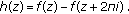
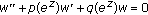 Nagoya Mathematical Journal 1967, 30: 29–37.
Nagoya Mathematical Journal 1967, 30: 29–37.