- Research Article
- Open access
- Published:
Generalized Bihari Type Integral Inequalities and the Corresponding Integral Equations
Journal of Inequalities and Applications volume 2009, Article number: 409809 (2009)
Abstract
We study some special nonlinear integral inequalities and the corresponding integral equations in measure spaces. They are significant generalizations of Bihari type integral inequalities and Volterra and Fredholm type integral equations. The kernels of the integral operators are determined by concave functions. Explicit upper bounds are given for the solutions of the integral inequalities. The integral equations are investigated with regard to the existence of a minimal and a maximal solution, extension of the solutions, and the generation of the solutions by successive approximations.
1. Introduction and the Main Results
In this paper we study integral inequalities of the form

and the corresponding integral equations

where
 is a measure space;
is a measure space;
 is a function from
is a function from  into
into  such that the following properties hold:
such that the following properties hold:
 for every
for every  ,
,
if  , then
, then  ,
,
 is
is  -measurable;
-measurable;
 is a function from
is a function from  into
into  with the following conditions:
with the following conditions:
 is concave,
is concave,
 ;
;
the functions  and
and  belong to
belong to

It may be noted that under the condition ( ) the function
) the function  is increasing (see Lemma 2.1 for the justification).
is increasing (see Lemma 2.1 for the justification).

always represents a  -algebra in
-algebra in  . The
. The  -integrable functions over a measurable set
-integrable functions over a measurable set  are considered to be
are considered to be  -almost measurable on
-almost measurable on  . The product of the measure space
. The product of the measure space  with itself is understood as in [1], and it is denoted by
with itself is understood as in [1], and it is denoted by  .
.
By  we designate the set of nonnegative integers.
we designate the set of nonnegative integers.
Special cases of (1.1) seem first to have been investigated by Lasalle [2] and Bihari [3]. Bihari's classical result gives an explicit upper bound for the solutions of the integral inequality

where  ,
,  and
and  are nonnegative continuous functions on
are nonnegative continuous functions on  , and
, and  is a positive continuous and increasing function on
is a positive continuous and increasing function on  . A group of inequalities is now associated with Bihari's name. Results for the various forms of such inequalities and references to different works in this topic can be found in [4–6]. Bihari type inequalities have been widely studied because they can be applied in the theory of difference, differential and integral equations. Riemann or classical Lebesgue integral is used in most of the theorems in this area. There are relatively few papers using other types of integral. For generalizations to abstract Lebesgue integral; see [7–9]. The linear version of (1.1) is given in [7]. The special case
. A group of inequalities is now associated with Bihari's name. Results for the various forms of such inequalities and references to different works in this topic can be found in [4–6]. Bihari type inequalities have been widely studied because they can be applied in the theory of difference, differential and integral equations. Riemann or classical Lebesgue integral is used in most of the theorems in this area. There are relatively few papers using other types of integral. For generalizations to abstract Lebesgue integral; see [7–9]. The linear version of (1.1) is given in [7]. The special case  ,
,  ,
,  of (1.1) is considered in [8], while the special case
of (1.1) is considered in [8], while the special case  ,
,  ,
,  of (1.1) is discussed in [9]. It turns out to be useful to study Bihari type inequalities with abstract Lebesgue integral. It is motivated proceeding in this direction as follows. We can get new facts about the nature of Bihari type inequalities even in the finite dimensional environment; the results can be applied in the study of certain new classes of differential and integral equations (see [7–11]).
of (1.1) is discussed in [9]. It turns out to be useful to study Bihari type inequalities with abstract Lebesgue integral. It is motivated proceeding in this direction as follows. We can get new facts about the nature of Bihari type inequalities even in the finite dimensional environment; the results can be applied in the study of certain new classes of differential and integral equations (see [7–11]).
The traditional treatment assumes not only that  , but also that the sets
, but also that the sets  ,
,  are intervals, while the present treatment (it should be emphasized that the methods employed to establish our results are not usual in this topic) makes it possible to consider more general sets (examples for functions satisfying (A
are intervals, while the present treatment (it should be emphasized that the methods employed to establish our results are not usual in this topic) makes it possible to consider more general sets (examples for functions satisfying (A ) and (A
) and (A ) can be found in [11]). Such results are not quite so easy to find in literature, although they can be used as powerful tools in many fields of mathematics.
) can be found in [11]). Such results are not quite so easy to find in literature, although they can be used as powerful tools in many fields of mathematics.
Besides  , the following function spaces will play an important role.
, the following function spaces will play an important role.
Definition 1.1.
If  is a nonempty subset of
is a nonempty subset of  such that
such that  for every
for every  , then let
, then let

Next, the basic concepts of the solutions of the inequalities (1.1) and

and the equation (1.2) are defined.
Definition 1.2.
We say that a function  is a solution of (1.1), (1.6), or (1.2) if
is a solution of (1.1), (1.6), or (1.2) if
(i) is a nonempty subset of
is a nonempty subset of  such that
such that  for every
for every  ,
,
(ii) ,
,
(iii) satisfies (1.1), (1.6), or (1.2) for each
satisfies (1.1), (1.6), or (1.2) for each  .
.
It is easily verified (see Lemma 2.5) that if  is a solution of (1.1), (1.6), or (1.2), then
is a solution of (1.1), (1.6), or (1.2), then  is
is  -integrable over
-integrable over  for all
for all  .
.
After these preparations we set ourselves the task of obtaining an upper bound for the solutions of (1.1). The following definition will be useful.
Definition 1.3.
-
(a)
For every
 with
with  , let
, let

Let

By ( ),
),  is a nonnegative real number for every
is a nonnegative real number for every  .
.
Now we are in a position to formulate the first main result.
Theorem 1.4.
Assume the conditions ( )–(
)–( ).
).
(a)Every solution  of (1.1) satisfies
of (1.1) satisfies

(b)The function  defined on
defined on  by
by

belongs to  .
.
In the second main result we test the scope of the previous theorem by applying it to prove the existence of a maximal and a minimal solution of the integral equation (1.2). At the same time, we show that every solution has maximal domain of existence  , and we apply the method of successive approximations to (1.2). Moreover, the behavior of the solutions is studied in a special case. The considered integral equations are in a very general form, there are classical Volterra and Fredholm type integral equations among them.
, and we apply the method of successive approximations to (1.2). Moreover, the behavior of the solutions is studied in a special case. The considered integral equations are in a very general form, there are classical Volterra and Fredholm type integral equations among them.
Theorem 1.5.
Suppose the conditions ( )–(
)–( ).
).
There exists a solution  of (1.2), which is minimal in the sense that
of (1.2), which is minimal in the sense that  ,
,  whenever
whenever  is a solution of (1.6).
is a solution of (1.6).
There exists a solution  of (1.2), which is maximal in the sense that
of (1.2), which is maximal in the sense that  ,
,  whenever
whenever  is a solution of (1.1).
is a solution of (1.1).
If  is a solution of (1.2), then
is a solution of (1.2), then  has an extension
has an extension  to
to  that is a solution of (1.2) on
that is a solution of (1.2) on  .
.
(c)Let  be a solution of (1.1). Then the successive approximations determined by
be a solution of (1.1). Then the successive approximations determined by 

are well defined,  ,
,  ; the sequence
; the sequence  is increasing and converges pointwise on
is increasing and converges pointwise on  to a solution of (1.2).
to a solution of (1.2).
(d)Let  be a solution of (1.6). Then the successive approximations (1.11) determined by
be a solution of (1.6). Then the successive approximations (1.11) determined by  are well defined,
are well defined,  ,
,  , and the sequence
, and the sequence  is decreasing. Moreover, if either
is decreasing. Moreover, if either  is continuous (at
is continuous (at  ) or
) or  , then they converge pointwise on
, then they converge pointwise on  to a solution of (1.2).
to a solution of (1.2).
(e)If in addition  and
and  are bounded on
are bounded on  for all
for all  , then every solution
, then every solution  of (1.2) is bounded on
of (1.2) is bounded on  for all
for all  .
.
We conclude this section with some remarks.
Remark 1.6.
The next example shows that the concavity of  alone does not imply neither the existence of an upper bound for the solutions of the integral inequality (1.1) nor the existence of a solution of the integral equation (1.2). Consider the integral inequality
alone does not imply neither the existence of an upper bound for the solutions of the integral inequality (1.1) nor the existence of a solution of the integral equation (1.2). Consider the integral inequality

and the corresponding integral equation

where  is the unit mass at
is the unit mass at  defined on the
defined on the  -algebra of Borel subsets of
-algebra of Borel subsets of  , and
, and

Then the conditions ( )–(
)–( ) are satisfied without (
) are satisfied without ( ). It is obvious that the functions
). It is obvious that the functions

are solutions of (1.12), showing that there are no either global or local upper bounds for the solutions of (1.12). It is easy to check that (1.13) has no solution.
Remark 1.7.
It is illustrated by an example that under the conditions ( )–(
)–( ) the maximal domain of existence of a solution of (1.1) may be a proper subset of
) the maximal domain of existence of a solution of (1.1) may be a proper subset of  . Let
. Let  , let
, let  be the Lebesgue measurable subsets of
be the Lebesgue measurable subsets of  , and let
, and let  be the Lebesgue measure on
be the Lebesgue measure on  . The function
. The function  is defined on
is defined on  by
by

The functions  and
and  are defined on
are defined on  by
by  . Suppose
. Suppose  ,
,  . Then (
. Then ( )–(
)–( ) are satisfied. Let
) are satisfied. Let  be a non (Lebesgue) measurable function. Then
be a non (Lebesgue) measurable function. Then  is a solution of (1.1) which has no extension to
is a solution of (1.1) which has no extension to  .
.
Remark.
The following example makes it clear that some extra conditions for  are necessary in Theorem 1.5(d). Let
are necessary in Theorem 1.5(d). Let

let  be the power set of
be the power set of  , and let the measure
, and let the measure  be defined on
be defined on  by
by

where the measure 
 is the unit mass at
is the unit mass at  defined on
defined on  . We consider the integral equation
. We consider the integral equation

where  ,
,  , and
, and

The conditions ( )–(
)–( ) can be immediately verified. Define the function
) can be immediately verified. Define the function  by
by  . Noting that
. Noting that  leads to the inequality
leads to the inequality

A few easy calculations imply that, for every 

and therefore

Since (1.19) has the unique solution  ,
,  , then the successive approximations
, then the successive approximations  do not converge to the solution of (1.19).
do not converge to the solution of (1.19).
2. Preliminaries
This section is devoted to some preparatory results. In the following three lemmas we establish some useful properties of concave functions.
Lemma 2.1.
If the function  is concave, then
is concave, then  is increasing.
is increasing.
Proof.
Suppose that there exist  for which
for which  . By the concavity of
. By the concavity of  , the points of the graph of
, the points of the graph of  are below or on the ray from
are below or on the ray from  through
through  for all
for all  , and therefore
, and therefore

Since

it follows from (2.1) that  if
if  is large enough. This contradicts the range of
is large enough. This contradicts the range of  .
.
Lemma 2.2.
Suppose the function  is concave,
is concave,  , and
, and  . Associate to
. Associate to  the nonnegative real number
the nonnegative real number

Then
(a) is strictly decreasing on
is strictly decreasing on  ;
;
(b) for all
for all  ;
;
(c)If  , and there is a
, and there is a  such that
such that  , then
, then  for all
for all  .
.
Proof.
The hypotheses on  (since
(since  is concave,
is concave,  is continuous on
is continuous on  ) guarantee that exactly one of the following three cases holds:
) guarantee that exactly one of the following three cases holds:
(i) and
and  for all
for all  ;
;
(ii)there exists a  such that
such that  for all
for all  and
and  for all
for all  ;
;
(iii)there is a unique  such that
such that  ,
,  for all
for all  and
and  for all
for all  .
.
It follows that  if (i) is satisfied, and
if (i) is satisfied, and  otherwise. At the same time (b) and (c) are proved.
otherwise. At the same time (b) and (c) are proved.
It remains to show (a). If  , then (i)–(iii) show that
, then (i)–(iii) show that  . Assume
. Assume  . By the concavity of
. By the concavity of  ,
,

and hence

The proof is complete.
Lemma 2.3.
Suppose the function  is concave, and
is concave, and  . Associate to
. Associate to  and to each of the nonnegative real numbers
and to each of the nonnegative real numbers  ,
,  the function
the function

Then
(a) is concave, and
is concave, and  ;
;
(b)If  ,
,  , then
, then  , where
, where

(c)If  and
and  , then
, then  uniformly on
uniformly on  as
as  in
in  ;
;
(d)the function  defined on
defined on  is upper semicontinuous.
is upper semicontinuous.
Proof.
-
(a)
It is obvious.
By (a), Lemma 2.2(b) and (a) give the result.
The triangle inequality insures that

Then from Lemma 2.1

and this gives the result.
To prove this, choose  , and
, and  . The definition of
. The definition of  and Lemma 2.2(a) imply that
and Lemma 2.2(a) imply that

By (b),  uniformly on
uniformly on  as
as  in
in  , and hence there exists a neighborhood
, and hence there exists a neighborhood  of
of  in
in  such that
such that

It now follows from Lemma 2.2 (a) that

and the proof is complete.
The next result was proved in [8, Lemma  (b)].
(b)].
Lemma 2.4.
Suppose that ( ) and (
) and ( ) hold. Let
) hold. Let  such that
such that  for every
for every  . Suppose
. Suppose  is
is  -integrable over
-integrable over  ,
,  is
is  -almost measurable on
-almost measurable on  , and there exists a measurable subset
, and there exists a measurable subset  of
of  such that
such that  is
is  -finite and
-finite and  for all
for all  . Then the function
. Then the function

is  -almost measurable on
-almost measurable on  .
.
Lemma 2.5.
Assume the conditions ( )–(
)–( ). If
). If  is a nonempty subset of
is a nonempty subset of  such that
such that  for every
for every  and
and  , then
, then  .
.
Proof.
Let  be fixed. Since
be fixed. Since  is increasing it is Borel measurable. Consequently, since
is increasing it is Borel measurable. Consequently, since  is
is  -almost measurable on
-almost measurable on  ,
,  is
is  -almost measurable on
-almost measurable on  . By (A
. By (A ), we can find
), we can find  such that
such that  for all
for all  . Hence, note that
. Hence, note that  is increasing:
is increasing:

It now follows from the definition of  and from (
and from ( ) that
) that  is
is  -integrable over
-integrable over  . The proof is complete.
. The proof is complete.
A consequence of the previous results that will be important later on is follows.
Lemma 2.6.
Suppose that ( )–(
)–( ) hold. If
) hold. If  is a nonempty subset of
is a nonempty subset of  such that
such that  for every
for every  and
and  , then the function
, then the function

belongs to  .
.
Proof.
Let  .
.
By Lemma 2.4, the function

is  -almost measurable on
-almost measurable on  . Hence it follows from the
. Hence it follows from the  -integrability of
-integrability of  and
and  over
over  (the latter can be seen from Lemma 2.5), combined with the inequality
(the latter can be seen from Lemma 2.5), combined with the inequality

that the function (2.16) is  -integrable over
-integrable over  . We conclude that the function (2.15) is
. We conclude that the function (2.15) is  -integrable over
-integrable over  .
.
The proof is complete.
We need the concept of AL-space, which is of fundamental significance in the proof of Theorem 1.5.
Definition 2.7.
Suppose ( ), and let
), and let  be a nonempty set from
be a nonempty set from  .
.
(a)Let

For a given  , the symbol
, the symbol  is defined by
is defined by  .
.
(b)Let  , and let
, and let  . For every
. For every  , let
, let  be the equivalence class containing
be the equivalence class containing 
 , and we set
, and we set  .
.
(c)We introduce the canonical ordering on  : for
: for  ,
,  , and
, and  means that
means that  -almost everywhere on
-almost everywhere on  .
.
Remark 2.8.
-
(a)

is a complete pseudometric space.
 is an
is an  -normed Banach lattice, briefly,
-normed Banach lattice, briefly,  -space (see [12]).
-space (see [12]).
If  is a function and
is a function and  is a subset of the domain of
is a subset of the domain of  , then the restriction of
, then the restriction of  to
to  is denoted by
is denoted by  .
.
Lemma 2.9.
Suppose ( ), and let
), and let  and
and  be nonempty sets from
be nonempty sets from  such that
such that  . If
. If  and
and  are nonempty majorized subsets of
are nonempty majorized subsets of  such that
such that  , then
, then

Proof.
Since  is an
is an  -space, it is order complete (see [12]), and hence
-space, it is order complete (see [12]), and hence  and
and  exist. Let
exist. Let  and
and  . Then
. Then  -almost everywhere on
-almost everywhere on  , thus the function
, thus the function

is an upper bound of  . It follows that
. It follows that  , that is
, that is  -almost everywhere on
-almost everywhere on  . An argument entirely similar to the preceding part gives that
. An argument entirely similar to the preceding part gives that  , where
, where

and therefore  -almost everywhere on
-almost everywhere on  .
.
The proof is now complete.
The next result can be found in [11, Lemma  ].
].
Lemma 2.10.
Assume that the hypotheses ( ), (
), ( ), (
), ( ), and (
), and ( ) are satisfied. Let
) are satisfied. Let  . Suppose we are given solutions
. Suppose we are given solutions  ,
,  of (1.2) such that
of (1.2) such that  for each
for each  ,
,  with
with  . Then there exists exactly one solution
. Then there exists exactly one solution  of (1.2) for which
of (1.2) for which  ,
,  .
.
3. Proofs of the Main Results
Consider now the proof of Theorem 1.4.
Proof.
-
(a)
If
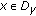 such that
such that 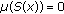 , then (1.9) follows directly from (1.1).
, then (1.9) follows directly from (1.1).
Now, fix a point  with
with  . To estimate the second term on the right of (1.1), we can apply Jensen's inequality (see [13]), by (
. To estimate the second term on the right of (1.1), we can apply Jensen's inequality (see [13]), by ( ):
):

and therefore

This inequality, together with Definition 1.3(a), implies that the expression

satisfies the inequality

By Lemma 2.3 (b) and Definition 1.3 (b),  , and hence (1.9) can be deduced from
, and hence (1.9) can be deduced from


The properties defining  are trivial if
are trivial if  with
with  . So assume
. So assume  such that
such that  .
.
First, we show that the function  is
is  -almost measurable on
-almost measurable on  . It is an easy consequence of (
. It is an easy consequence of ( ) and Lemma 2.4 that the functions
) and Lemma 2.4 that the functions


are  -almost measurable on
-almost measurable on  . This means that there exists a measurable subset
. This means that there exists a measurable subset  of
of  such that
such that  and (3.6), (3.7) are measurable on
and (3.6), (3.7) are measurable on  . Further, since
. Further, since  is
is  -almost measurable on
-almost measurable on  , it can be supposed that
, it can be supposed that  is measurable on
is measurable on  . Thus we need to show that the function
. Thus we need to show that the function

is measurable on  . To prove this let
. To prove this let

The measurability of (3.6) on  implies that
implies that  . Since
. Since

it is enough to show that (3.8) is measurable on  . It follows from the definitions of
. It follows from the definitions of  and
and  that the function
that the function

is measurable. Hence, by Lemma 2.3 (d), (3.8) is measurable on  .
.
It is now clear that  is
is  -almost measurable on
-almost measurable on  .
.
Next, we prove that  is
is  -integrable over
-integrable over  .
.
To prove this, it is enough to show that the function

is bounded on  . Since
. Since

we need to verify that (3.12) is bounded on  . By (
. By ( ), we can find a
), we can find a  such that
such that

It therefore follows from

that

for all  , and hence
, and hence

Thus

and therefore another application of (3.14) gives

and from this the claim follows. Consequently,  is
is  -integrable over
-integrable over  , as required.
, as required.
The result is completely proved.
Now we are in a position to prove Theorem 1.5.
Proof.
We begin with the proof of (c) and (d).
-
(c)
To prove that
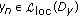 we use induction on
we use induction on  . Clearly
. Clearly 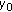 belongs to
belongs to 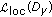 . Let
. Let 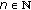 such that the assertion holds. Then Lemma 2.6 yields that
such that the assertion holds. Then Lemma 2.6 yields that 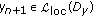 . We show now that the sequence
. We show now that the sequence 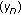 is increasing. By our hypotheses on
is increasing. By our hypotheses on 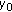 , it follows that
, it follows that 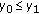 , and we again complete the proof by induction. Suppose
, and we again complete the proof by induction. Suppose 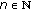 such that
such that 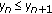 . Then, by Lemma 2.1 and the induction hypothesis
. Then, by Lemma 2.1 and the induction hypothesis

Since

Theorem 1.4(a) implies that

Because of (3.22) and the fact that  is increasing, there exists a function
is increasing, there exists a function  such that
such that  converges pointwise on
converges pointwise on  to
to  . Then
. Then  is a consequence of
is a consequence of  together with (3.22), Lemma 2.1(a) and, Theorem 1.4(b). If
together with (3.22), Lemma 2.1(a) and, Theorem 1.4(b). If  with
with  , then according to the continuity of
, then according to the continuity of  on
on  ,
,  converges to
converges to  . Let
. Let  with
with  . As we have seen
. As we have seen  is increasing, and therefore
is increasing, and therefore  for all
for all  . Consequently
. Consequently

Now (1.11) and the monotone convergence theorem give that  is a solution of (1.2).
is a solution of (1.2).
-
(d)
We can see exactly as in the proof of (c) that
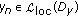 ,
, 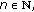 and the sequence
and the sequence  is decreasing. It follows from an easy induction argument that
is decreasing. It follows from an easy induction argument that  is nonnegative for all
is nonnegative for all 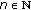 . Linking up with the foregoing, there exists a function
. Linking up with the foregoing, there exists a function  such that
such that  converges pointwise on
converges pointwise on 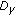 to
to 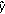 .
. 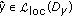 can be shown as in the proof of (c).
can be shown as in the proof of (c).
The continuity of  on
on  implies that
implies that  converges to
converges to  for every
for every  .
.
Assume now that  . If
. If  such that
such that  for every large enough
for every large enough  , then
, then

If  such that
such that  for every
for every  , then
, then

which leads to  . In both cases
. In both cases  converges to
converges to  for every
for every  .
.
According to (1.11) and the monotone convergence theorem  is a solution of (1.2).
is a solution of (1.2).
( ) For convergence of the successive approximations
) For convergence of the successive approximations

to a solution  of (1.2) it suffices, in view of (c), to show that
of (1.2) it suffices, in view of (c), to show that  is a solution of (1.1), which is evident. It remains to prove that if
is a solution of (1.1), which is evident. It remains to prove that if  is a solution of (1.6), then
is a solution of (1.6), then  for every
for every  . To this end, it is enough to show that
. To this end, it is enough to show that

This is true for  , since the functions
, since the functions  and
and  are nonnegative. Let
are nonnegative. Let  for which the result holds. Then, because of the nonnegativity of
for which the result holds. Then, because of the nonnegativity of  and the fact that
and the fact that  is increasing,
is increasing,

and the proof of the induction step is complete.
( ) Let
) Let

Choose  . The set of the upper bounds from
. The set of the upper bounds from  for the solutions of (1.1) on
for the solutions of (1.1) on  is denoted by
is denoted by  . By Theorem 1.4,
. By Theorem 1.4,  is not empty. Let
is not empty. Let

Then  is a minorized subset of
is a minorized subset of  (the elements of
(the elements of  are nonnegative). Since this space is order complete (see [12]),
are nonnegative). Since this space is order complete (see [12]),

exists. Let  , and let
, and let  be a solution of (1.1) such that
be a solution of (1.1) such that  .
.  ,
,  gives that
gives that

It follows that

because  is increasing. Since
is increasing. Since  the proof of Lemma 2.5 shows that
the proof of Lemma 2.5 shows that  , and hence by (
, and hence by ( ), the function
), the function  defined by
defined by

belongs to  , and therefore
, and therefore  . It now comes from (3.33) and the definition of
. It now comes from (3.33) and the definition of  that
that

Since  is increasing,
is increasing,

and thus

We can see that

If we set

then (3.38) shows that  is a solution of (1.2). (3.33) gives that
is a solution of (1.2). (3.33) gives that

for every solutions  of (1.1) for which
of (1.1) for which  .
.
Repeat the preceding construction for every  . We thus obtain a set of functions
. We thus obtain a set of functions  , each a solution of (1.2) on its domain. Moreover, if
, each a solution of (1.2) on its domain. Moreover, if  is a solution of (1.1), then for every
is a solution of (1.1), then for every  we have
we have

Introduce the next functions: for every  with
with  let the function
let the function  be defined on
be defined on  by
by

Obviously, these functions are also solutions of (1.2) on their domains.
Now let  ,
,  such that
such that  and
and  . Using (3.41), it is easy to verify that
. Using (3.41), it is easy to verify that

and therefore Lemma 2.10 is applicable to the solutions  . This gives a unique solution
. This gives a unique solution  of (1.2) for which
of (1.2) for which

It remains to prove that  is maximal. Let
is maximal. Let  be a solution of (1.1), and let
be a solution of (1.1), and let  . If
. If  , then
, then

while if  , then by (3.41)
, then by (3.41)

so that Lemma 2.1 implies that


We first show that every solution  of (1.2) with
of (1.2) with  has an extension
has an extension  that is a solution of (1.2) such that
that is a solution of (1.2) such that  is a proper subset of
is a proper subset of  . This follows from (c) as soon as it is realized that every solution
. This follows from (c) as soon as it is realized that every solution  of (1.2) with
of (1.2) with  has an extension
has an extension  that is a solution of (1.1) such that
that is a solution of (1.1) such that  is a proper subset of
is a proper subset of  . Really, in this case the successive approximations determined by
. Really, in this case the successive approximations determined by  converge to a solution
converge to a solution  of (1.2), which is obviously an extension of
of (1.2), which is obviously an extension of  .
.
That realization can be reached in finitely many steps.
Let  be a solution of (1.2) with
be a solution of (1.2) with  , and let
, and let  .
.
-
(i)
Suppose
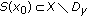 .
.
If  , then
, then

is an appropriate solution.
If  , then
, then

is a solution of (1.1) that agrees with  on
on  .
.
-
(ii)
Suppose
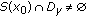 and
and  . Let
. Let

If  , then the function
, then the function

is a solution of (1.1) ( ,
,  , thus
, thus  ) that agrees with
) that agrees with  on
on  .
.
If  , then we introduce the functions
, then we introduce the functions  ,
,  ,
,

which all lie in  , and they are all solutions of (1.1). By Theorem 1.4 (b),
, and they are all solutions of (1.1). By Theorem 1.4 (b),  is a majorized subset of
is a majorized subset of  . Since this space is order complete (see [12]),
. Since this space is order complete (see [12]),

exists. Choose  . Then
. Then  -almost everywhere on
-almost everywhere on  for every
for every  , and therefore Lemma 2.1 yields that
, and therefore Lemma 2.1 yields that

Since  the proof of Lemma 2.5 shows that
the proof of Lemma 2.5 shows that  , and hence by (A
, and hence by (A ), the function
), the function

belongs to  too. It now follows from
too. It now follows from  and (3.54) that
and (3.54) that

We set

By (3.56)

Fix  . From Lemma 2.9 (with
. From Lemma 2.9 (with  and
and  there being
there being  and
and  resp.) we get that
resp.) we get that  -almost everywhere on
-almost everywhere on  , and hence
, and hence

Consequently,  ,
,  . If
. If  with
with  , then
, then  . We can see that
. We can see that

By what we have already proved that

is a solution of (1.1) that agrees with  on
on  .
.
-
(iii)
Suppose
 and
and 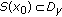 . By an argument entirely similar to that for the case (ii), we can get a solution
. By an argument entirely similar to that for the case (ii), we can get a solution 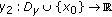 of (1.1) that agrees with
of (1.1) that agrees with 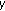 on
on 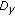 .
.
After these preparations, the proof can be concluded quickly. Let  be a solution of (1.2), and let
be a solution of (1.2), and let  be the set of all solutions of (1.2) which agree with
be the set of all solutions of (1.2) which agree with  on
on  . Since
. Since  ,
,  is not empty. Partially order
is not empty. Partially order  by declaring
by declaring  to mean that the restriction of
to mean that the restriction of  to the domain of
to the domain of  agrees with
agrees with  . By Hausdorff's maximality theorem, there exists a maximal totally ordered subcollection
. By Hausdorff's maximality theorem, there exists a maximal totally ordered subcollection  of
of  . Let
. Let  be the union of the domains of all members of
be the union of the domains of all members of  , and define
, and define  by
by  , where
, where  occurs in
occurs in  . It is easy to check that
. It is easy to check that  is well defined, and it is a solution of (1.2). If
is well defined, and it is a solution of (1.2). If  were a proper subset of
were a proper subset of  , then the first part of the proof would give a further extension of
, then the first part of the proof would give a further extension of  , and this would contradict the maximality of
, and this would contradict the maximality of  .
.
-
(e)
Let
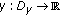 be a solution of (1.2), and let
be a solution of (1.2), and let 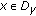 .
.
If  , then
, then  , so that
, so that  is bounded on
is bounded on  .
.
Suppose  . Since
. Since  and
and  are bounded on
are bounded on  and
and  is finite, Theorem 1.4 (a) implies that it is enough to prove the boundedness of the function
is finite, Theorem 1.4 (a) implies that it is enough to prove the boundedness of the function

on  . Moreover, we have only to observe that the function
. Moreover, we have only to observe that the function

is bounded on  . To prove this, let
. To prove this, let

If  and
and  ,
,  , then
, then  and
and  for every
for every  , and therefore by Lemma 2.3(d), the function (3.63) is bounded on
, and therefore by Lemma 2.3(d), the function (3.63) is bounded on  . If
. If  , then the definition of the function
, then the definition of the function  gives that
gives that  . The claim about
. The claim about  is therewith confirmed.
is therewith confirmed.
The proof of the theorem is now complete.
References
Horváth L: On the associativity of the product of measure spaces. Acta Mathematica Hungarica 2003,98(4):301–310. 10.1023/A:1022886211723
LaSalle J: Uniqueness theorems and successive approximations. Annals of Mathematics 1949, 50: 722–730. 10.2307/1969559
Bihari I: A generalization of a lemma of Bellman and its application to uniqueness problems of differential equations. Acta Mathematica Academiae Scientiarum Hungaricae 1956, 7: 81–94. 10.1007/BF02022967
Bainov D, Simeonov P: Integral Inequalities and Applications, Mathematics and Its Applications (East European Series). Volume 57. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1992:xii+245.
Mitrinovic DS, Pecaric JE, Fink AM: Inequalities Involving Functions and Their Integrals and Derivatives, Mathematics and Its Applications (East European Series). Volume 53. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1991:xvi+587.
Pachpatte BG: Integral and Finite Difference Inequalities and Applications, North-Holland Mathematics Studies. Volume 205. Elsevier Science, Amsterdam, The Netherlands; 2006:x+309.
Horváth L: Integral inequalities in measure spaces. Journal of Mathematical Analysis and Applications 1999,231(1):278–300. 10.1006/jmaa.1998.6251
Horváth L: Generalizations of special Bihari type integral inequalities. Mathematical Inequalities & Applications 2005,8(3):441–449.
Horváth L: Generalization of a Bihari type integral inequality for abstract Lebesgue integral. Journal of Mathematical Inequalities 2008,2(1):115–128.
Horváth L: Integral equations in measure spaces. Integral Equations and Operator Theory 2003,45(2):155–176. 10.1007/s000200300001
Horváth L: Nonlinear integral equations with increasing operators in measure spaces. Journal of Integral Equations and Applications 2005,17(4):413–437. 10.1216/jiea/1181075352
Schaefer HH: Banach Lattices and Positive Operators, Die Grundlehren der Mathematischen Wissenschaften, Band 21. Springer, New York, NY, USA; 1974:xi+376.
Hewitt E, Stromberg KR: Real and Abstract Analysis, Graduate Texts in Mathematics. Volume 25. Springer, Berlin, Germany; 1965.
Acknowledgment
This work was supported by Hungarian Foundation for Scientific Research Grant no. K73274.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Horváth, L. Generalized Bihari Type Integral Inequalities and the Corresponding Integral Equations. J Inequal Appl 2009, 409809 (2009). https://doi.org/10.1155/2009/409809
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/409809
 with
with  , let
, let
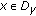 such that
such that 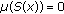 , then (1.9) follows directly from (1.1).
, then (1.9) follows directly from (1.1).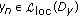 we use induction on
we use induction on  . Clearly
. Clearly 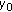 belongs to
belongs to 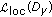 . Let
. Let 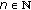 such that the assertion holds. Then Lemma 2.6 yields that
such that the assertion holds. Then Lemma 2.6 yields that 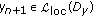 . We show now that the sequence
. We show now that the sequence 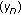 is increasing. By our hypotheses on
is increasing. By our hypotheses on 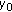 , it follows that
, it follows that 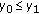 , and we again complete the proof by induction. Suppose
, and we again complete the proof by induction. Suppose 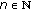 such that
such that 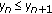 . Then, by Lemma 2.1 and the induction hypothesis
. Then, by Lemma 2.1 and the induction hypothesis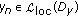 ,
, 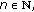 and the sequence
and the sequence  is decreasing. It follows from an easy induction argument that
is decreasing. It follows from an easy induction argument that  is nonnegative for all
is nonnegative for all 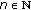 . Linking up with the foregoing, there exists a function
. Linking up with the foregoing, there exists a function  such that
such that  converges pointwise on
converges pointwise on 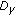 to
to 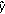 .
. 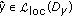 can be shown as in the proof of (c).
can be shown as in the proof of (c).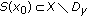 .
.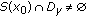 and
and  . Let
. Let and
and 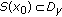 . By an argument entirely similar to that for the case (ii), we can get a solution
. By an argument entirely similar to that for the case (ii), we can get a solution 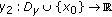 of (1.1) that agrees with
of (1.1) that agrees with 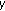 on
on 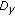 .
.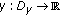 be a solution of (1.2), and let
be a solution of (1.2), and let 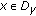 .
.