- Research Article
- Open access
- Published:
Weak Contractions, Common Fixed Points, and Invariant Approximations
Journal of Inequalities and Applications volume 2009, Article number: 390634 (2009)
Abstract
The existence of common fixed points is established for the mappings, where  is
is  -weak contraction on a nonempty subset of a Banach space. As application, some results on the invariant best approximation are proved. Our results unify and substantially improve several recent results given by some authors.
-weak contraction on a nonempty subset of a Banach space. As application, some results on the invariant best approximation are proved. Our results unify and substantially improve several recent results given by some authors.
1. Introduction and Preliminaries
Let  be a subset of a normed space
be a subset of a normed space  . The set
. The set

is called the set of best approximants to  out of
out of  where
where

We denote  and
and  (resp.,
(resp.,  ) by the set of positive integers and the closure (resp., weak closure) of a set
) by the set of positive integers and the closure (resp., weak closure) of a set  in
in  , respectively. Let
, respectively. Let  be mappings. The set of fixed points of
be mappings. The set of fixed points of  is denoted by
is denoted by  . A point
. A point  is a coincidence point (resp., common fixed point) of
is a coincidence point (resp., common fixed point) of  and
and  if
if  (resp.,
(resp.,  ). The set of coincidence points of
). The set of coincidence points of  and
and  is denoted by
is denoted by 
The pair  is said to be
is said to be
(1)commuting [1] if  for all
for all 
(2)compatible [2, 3] if  whenever
whenever  is a sequence such that
is a sequence such that  for some
for some  in
in  ,
,
(3)weakly compatible if they commute at their coincidence points, that is, if  whenever
whenever  ,
,
(4)a Banach operator pair if the set  is
is  -invariant, namely,
-invariant, namely,  .
.
Obviously, the commuting pair  is a Banach operator pair, but converse is not true in general (see [4, 5].) If
is a Banach operator pair, but converse is not true in general (see [4, 5].) If  is a Banach operator pair, then
is a Banach operator pair, then  needs not be a Banach operator pair (see [4, Example 1]).
needs not be a Banach operator pair (see [4, Example 1]).
The set  is said to be
is said to be  -starshaped with
-starshaped with  if the segment
if the segment  joining
joining  to
to  is contained in
is contained in  for all
for all  The mapping
The mapping  defined on a
defined on a  -starshaped set
-starshaped set  is said to be affine if
is said to be affine if

Suppose that the set  is
is  -starshaped with
-starshaped with  and is both
and is both  - and
- and  -invariant. Then
-invariant. Then  and
and  are said to be
are said to be
(5) -commuting [3, 6] if
-commuting [3, 6] if  for all
for all  , where
, where  where
where  ,
,
(6)pointwise  -subweakly commuting [7] if, for given
-subweakly commuting [7] if, for given  there exists a real number
there exists a real number  such that
such that  ,
,
(7) -subweakly commuting on
-subweakly commuting on  [8] if, for all
[8] if, for all  there exists a real number
there exists a real number  such that
such that  .
.
In 1963, Meinardus [9] employed Schauder's fixed point theorem to prove a result regarding invariant approximation. Further, some generalizations of the result of Meinardus were obtained by Habiniak [10], Jungck and Sessa [11], and Singh [12].
Since then, Al-Thagafi [13] extended these works and proved some results on invariant approximations for commuting mappings. Hussain and Jungck [8], Hussain [5], Jungck and Hussain [3], O'Regan and Hussain [7], Pathak and Hussain [14], and Pathak et al. [15] extended the work of Al-Thagafi [13] for more general noncommuting mappings.
Recently, Chen and Li [4] introduced the class of Banach operator pairs as a new class of noncommuting mappings and it has been further studied by Hussain [5], Khan and Akbar [16], and Pathak and Hussain [14].
In this paper, we extend and improve the recent common fixed point and invariant approximation results of Al-Thagafi [13], Al-Thagafi and Shahzad [17], Berinde [18], Chen and Li [4], Habiniak [10], Jungck and Sessa [11], Pathak and Hussain [14], and Singh [12] to the class of  -weak contractions. The applications of the fixed point theorems are remarkable in diverse disciplines of mathematics, statistics, engineering, and economics in dealing with the problems arising in approximation theory, potential theory, game theory, theory of differential equations, theory of integral equations, and others (see [14, 15, 19, 20]).
-weak contractions. The applications of the fixed point theorems are remarkable in diverse disciplines of mathematics, statistics, engineering, and economics in dealing with the problems arising in approximation theory, potential theory, game theory, theory of differential equations, theory of integral equations, and others (see [14, 15, 19, 20]).
2. Main Results
Let  be a metric space. A mapping
be a metric space. A mapping  is called a weak contraction if there exist two constants
is called a weak contraction if there exist two constants  and
and  such that
such that

Remark 2.1.
Due to the symmetry of the distance, the weak contraction condition (2.1) includes the following:

which is obtained from (2.1) by formally replacing  ,
,  by
by  ,
,  , respectively, and then interchanging
, respectively, and then interchanging  and
and  .
.
Consequently, in order to check the weak contraction of  , it is necessary to check both (2.1) and (2.2). Obviously, a Banach contraction satisfies (2.1) and hence is a weak contraction. Some examples of weak contractions are given in [18, 21, 22]. The next example shows that a weak contraction needs not to be continuous.
, it is necessary to check both (2.1) and (2.2). Obviously, a Banach contraction satisfies (2.1) and hence is a weak contraction. Some examples of weak contractions are given in [18, 21, 22]. The next example shows that a weak contraction needs not to be continuous.
Let  be the unit interval with the usual norm and let
be the unit interval with the usual norm and let  be given by
be given by  for all
for all  and
and  . Then
. Then  satisfies the inequality (2.1) with
satisfies the inequality (2.1) with  and
and  and
and  has a unique fixed point
has a unique fixed point  , but
, but  is not continuous.
is not continuous.
Let  be a self-mapping on
be a self-mapping on  . A mapping
. A mapping  is said to be
is said to be  -weak contraction or
-weak contraction or  -weak contraction if there exist two constants
-weak contraction if there exist two constants  and
and  such that
such that

Berinde [18] introduced the notion of a  -weak contraction and proved that a lot of the well-known contractive conditions do imply the
-weak contraction and proved that a lot of the well-known contractive conditions do imply the  -weak contraction. The concept of
-weak contraction. The concept of  -weak contraction does not ask
-weak contraction does not ask  to be less than
to be less than  as happens in many kinds of fixed point theorems for the contractive conditions that involve one or more of the displacements
as happens in many kinds of fixed point theorems for the contractive conditions that involve one or more of the displacements  . For more details, we refer to [18, 21] and references cited in these papers.
. For more details, we refer to [18, 21] and references cited in these papers.
The following result is a consequence of the main theorem of Berinde [18].
Lemma 2.3.
Let  be a nonempty subset of a metric space
be a nonempty subset of a metric space  and let
and let  be a self-mapping of
be a self-mapping of  . Assume that
. Assume that  ,
,  is complete, and
is complete, and  is a
is a  -weak contraction. Then
-weak contraction. Then  is nonempty.
is nonempty.
Theorem 2.4.
Let  be a nonempty subset of a metric space
be a nonempty subset of a metric space  and let
and let  be self-mappings of
be self-mappings of  Assume that
Assume that  is nonempty,
is nonempty,  ,
,  is complete, and
is complete, and  is an
is an  -weak contraction. Then
-weak contraction. Then  .
.
Proof.
Since  is a closed subset of
is a closed subset of  ,
,  is complete. Further, by the
is complete. Further, by the  -weak contraction of
-weak contraction of  , for all
, for all  , we have
, we have

Hence  is a
is a  -weak contraction on
-weak contraction on  and
and  . Therefore, by Lemma 2.3,
. Therefore, by Lemma 2.3,  has a fixed point
has a fixed point  in
in  and so
and so  .
.
Corollary 2.5.
Let  be a nonempty subset of a metric space
be a nonempty subset of a metric space  and let
and let  be a Banach operator pair on
be a Banach operator pair on  . Assume that
. Assume that  is complete,
is complete,  is
is  -weak contraction, and
-weak contraction, and  is nonempty and closed. Then
is nonempty and closed. Then  .
.
In Theorem 2.4 and Corollary 2.5, if  , then we easily obtain the following result, which improves Lemma 3.1 of Chen and Li [4].
, then we easily obtain the following result, which improves Lemma 3.1 of Chen and Li [4].
Corollary 2.6 (see [17, Theorem 2.2]).
Let  be a nonempty subset of a metric space
be a nonempty subset of a metric space  and let
and let  be self-mappings of
be self-mappings of  Assume that
Assume that  is nonempty,
is nonempty,  ,
,  is complete, and
is complete, and  is an
is an  -contraction. Then
-contraction. Then  is a singleton.
is a singleton.
The following result properly contains [4, Theorems 3.2-3.3] and improves [13, Theorem 2.2], [10, Theorem 4], and [11, Theorem 6].
Theorem 2.7.
Let  be a nonempty subset of a normed (resp., Banach) space
be a nonempty subset of a normed (resp., Banach) space  and let
and let  be self-mappings of
be self-mappings of  Suppose that
Suppose that  is
is  -starshaped,
-starshaped,  (resp.,
(resp.,  ),
),  is compact (resp.,
is compact (resp.,  is weakly compact, and either
is weakly compact, and either  is demiclosed at
is demiclosed at  or
or  satisfies Opial's condition, where
satisfies Opial's condition, where  stands for the identity mapping), and there exists a constant
stands for the identity mapping), and there exists a constant  such that
such that

Then  .
.
Proof.
For each  , define
, define  by
by  for all
for all  and a fixed sequence
and a fixed sequence  of real numbers
of real numbers  converging to
converging to  . Since
. Since  is
is  -starshaped and
-starshaped and  (resp.,
(resp.,  ), we have
), we have  (resp.,
(resp.,  ) for each
) for each  . Also, by the inequality (2.5),
. Also, by the inequality (2.5),

for all  ,
,  , and
, and  Thus, for
Thus, for  ,
,  is a
is a  -weak contraction, where
-weak contraction, where  .
.
If  is compact, then, for each
is compact, then, for each  ,
,  is compact and hence complete. By Theorem 2.4, for each
is compact and hence complete. By Theorem 2.4, for each  , there exists
, there exists  such that
such that  The compactness of
The compactness of  implies that there exists a subsequence
implies that there exists a subsequence  of
of  such that
such that  as
as  . Since
. Since  is a sequence in
is a sequence in  and
and  , we have
, we have  . Further, it follows that
. Further, it follows that

Moreover, we have

Taking the limit as  we get
we get  and so
and so  .
.
Next, the weak compactness of  implies that
implies that  is weakly compact and hence complete due to completeness of
is weakly compact and hence complete due to completeness of  (see [3]). From Theorem 2.4, for each
(see [3]). From Theorem 2.4, for each  , there exists
, there exists  such that
such that  The weak compactness of
The weak compactness of  implies that there is a subsequence
implies that there is a subsequence  of
of  converging weakly to
converging weakly to  as
as  . Since
. Since  is a sequence in
is a sequence in  , we have
, we have  . Also, we have
. Also, we have  as
as  . If
. If  is demiclosed at
is demiclosed at  , then
, then  and so
and so 
If  then we have
then we have

which is a contradiction. Thus  and hence
and hence  This completes the proof.
This completes the proof.
Obviously,  -nonexpansive mappings satisfy the inequality (2.5) and so we obtain the following.
-nonexpansive mappings satisfy the inequality (2.5) and so we obtain the following.
Corollary 2.8 (see [17, Theorem 2.4]).
Let  be a nonempty subset of a normed (resp., Banach) space
be a nonempty subset of a normed (resp., Banach) space  and let
and let  ,
,  be self-mappings of
be self-mappings of  Suppose that
Suppose that  is
is  -starshaped,
-starshaped,  (resp.,
(resp.,  ),
),  is compact, (resp.,
is compact, (resp.,  is weakly compact, and either
is weakly compact, and either  is demiclosed at
is demiclosed at  or
or  satisfies Opial's condition), and
satisfies Opial's condition), and  is
is  -nonexpansive on
-nonexpansive on  . Then
. Then  .
.
Corollary 2.9 (see [4, Theorems 3.2-3.3]).
Let  be a nonempty subset of a normed (resp., Banach) space
be a nonempty subset of a normed (resp., Banach) space  and let
and let  be self-mappings of
be self-mappings of  Suppose that
Suppose that  is
is  -starshaped and closed (resp., weakly closed),
-starshaped and closed (resp., weakly closed),  is compact (resp.,
is compact (resp.,  is weakly compact, and either
is weakly compact, and either  is demiclosed at
is demiclosed at  or
or  satisfies Opial's condition),
satisfies Opial's condition),  is a Banach operator pair, and
is a Banach operator pair, and  is
is  -nonexpansive on
-nonexpansive on  . Then
. Then  .
.
Corollary 2.10 (see [13, Theorem 2.1]).
Let  be a nonempty closed and
be a nonempty closed and  -starshaped subset of a normed space
-starshaped subset of a normed space  and let
and let  ,
,  be self-mappings of
be self-mappings of  such that
such that  . Suppose that
. Suppose that  commutes with
commutes with  and
and  . If
. If  is compact,
is compact,  is continuous, linear, and
is continuous, linear, and  is
is  -nonexpansive on
-nonexpansive on  , then
, then  .
.
Let  where
where 
Corollary 2.11.
Let  be a normed (resp., Banach) space
be a normed (resp., Banach) space  and let
and let  be self-mappings of
be self-mappings of  If
If  ,
,  ,
,  is
is  -starshaped,
-starshaped,  (resp.,
(resp.,  ),
),  is compact, (resp.,
is compact, (resp.,  is weakly compact, and
is weakly compact, and  is demiclosed at
is demiclosed at  ). If the inequality (2.5) holds for all
). If the inequality (2.5) holds for all  then
then  .
.
Corollary 2.12.
Let  be a normed (resp., Banach) space
be a normed (resp., Banach) space  and let
and let  be self-mappings of
be self-mappings of  If
If  ,
,  ,
,  is
is  -starshaped,
-starshaped,  (resp.,
(resp.,  ),
),  is compact, (resp.,
is compact, (resp.,  is weakly compact, and
is weakly compact, and  is demiclosed at
is demiclosed at  ). If the inequality (2.5) holds for all
). If the inequality (2.5) holds for all  then
then  .
.
Corollary 2.13 (see [11, Theorem 7]).
Let  ,
,  be self-mappings of a Banach space
be self-mappings of a Banach space  with
with  and
and  with
with  . Suppose that
. Suppose that  is q-starshaped with
is q-starshaped with  ,
,  , and
, and  is affine, continuous in the weak and strong topology on
is affine, continuous in the weak and strong topology on  . If
. If  and
and  are commuting on
are commuting on  and
and  is
is  -nonexpansive on
-nonexpansive on  , then
, then  provided either (i)
provided either (i)  is weakly compact and
is weakly compact and  is demiclosed or (ii)
is demiclosed or (ii)  is weakly compact and
is weakly compact and  satisfies Opial's condition.
satisfies Opial's condition.
Remark 2.14.
Corollary 2.5 in [17] and Theorems 4.1-4.2 of Chen and Li [4] are special cases of Corollaries 2.11-2.12
We denote  by the class of closed convex subsets of
by the class of closed convex subsets of  containing
containing  . For any
. For any  , we define
, we define  It is clear that
It is clear that  (see [8, 13]).
(see [8, 13]).
Theorem 2.15.
Let  be self-mappings of a normed (resp., Banach) space
be self-mappings of a normed (resp., Banach) space  . If
. If  and
and  such that
such that  ,
,  is compact (resp.,
is compact (resp.,  is weakly compact), and
is weakly compact), and  for all
for all  , then
, then  is nonempty closed and convex with
is nonempty closed and convex with  . If, in addition,
. If, in addition,  ,
,  is
is  -starshaped,
-starshaped,  (resp.,
(resp.,  , and
, and  is demiclosed at
is demiclosed at  ), and the inequality (2.5) holds for all
), and the inequality (2.5) holds for all  then
then  .
.
Proof.
We may assume that  . If
. If  then
then  . Note that
. Note that

Thus  If
If  is compact, then, by the continuity of the norm, we get
is compact, then, by the continuity of the norm, we get  for some
for some  If we assume that
If we assume that  is weakly compact, then, using [23,Lemma 5.5, page 192], we can show the existence of a
is weakly compact, then, using [23,Lemma 5.5, page 192], we can show the existence of a  such that
such that  . Thus, in both cases, we have
. Thus, in both cases, we have

for all  Hence
Hence  and so
and so  is nonempty closed and convex with
is nonempty closed and convex with  . The compactness of
. The compactness of  (resp., the weak compactness of
(resp., the weak compactness of  ) implies that
) implies that  is compact (resp.,
is compact (resp.,  is weakly compact). Therefore, the result now follows from Corollary 2.12. This completes the proof.
is weakly compact). Therefore, the result now follows from Corollary 2.12. This completes the proof.
Corollary 2.16.
Let  be self-mappings of a normed (resp., Banach) space
be self-mappings of a normed (resp., Banach) space  . If
. If  and
and  such that
such that  ,
,  is compact (resp.,
is compact (resp.,  is weakly compact), and
is weakly compact), and  for all
for all  , then
, then  is nonempty closed and convex with
is nonempty closed and convex with  . If, in addition,
. If, in addition,  ,
,  is
is  -starshaped and closed (resp., weakly closed and
-starshaped and closed (resp., weakly closed and  is demiclosed at
is demiclosed at  ),
),  is a Banach operator pair on
is a Banach operator pair on  , and the inequality (2.5) holds for all
, and the inequality (2.5) holds for all  then
then  .
.
Remark 2.17.
Theorem 2.15 and Corollary 2.16 extend [13, Theorems 4.1 and 4.2], [17, Theorem 2.6], and [10, Theorem 8].
Banach's Fixed Point Theorem states that if  is a complete metric space,
is a complete metric space,  is a nonempty closed subset of
is a nonempty closed subset of  , and
, and  is a self-mapping satisfying the following condition: there exists
is a self-mapping satisfying the following condition: there exists  such that
such that

then  has a unique fixed point, say
has a unique fixed point, say  in
in  and the Picard iterative sequence
and the Picard iterative sequence  converges to the point
converges to the point  for all
for all  Since then, Ćirić [24] introduced and studied self-mappings on
Since then, Ćirić [24] introduced and studied self-mappings on  satisfying the following condition: there exists
satisfying the following condition: there exists  such that
such that

where

Further, many investigations were developed by Berinde [19], Jungck [1, 2], Hussain and Jungck [8], Hussain and Rhoades [6], O'Regan and Hussain [7], and many other mathematicians (see [14, 25] and references therein). Recently, Jungck and Hussain [3] proved the following extension of the result of Ćirić [24].
Theorem 2.18 (see [3, Theorem 2.1]).
Let  be a nonempty subset of a metric space
be a nonempty subset of a metric space  and let
and let  be self-mappings of
be self-mappings of  . Assume that
. Assume that  ,
,  is complete, and
is complete, and  ,
,  satisfy the following condition: there exists
satisfy the following condition: there exists  such that
such that

for all  . Then
. Then  .
.
The following result (Theorem 2.19) properly contains [17, Theorem 3.3], [4, Theorems 3.2-3.3], [5, Theorem 2.11], and [14, Theorem 2.2]. The proof is analogous to the proof of Theorem 2.7. In fact, instead of applying Theorem 2.4, we apply Theorem 2.18 to get the conclusion.
Theorem 2.19.
Let  be a nonempty subset of a normed (resp., Banach) space
be a nonempty subset of a normed (resp., Banach) space  and let
and let  be self-mappings of
be self-mappings of  Suppose that
Suppose that  is
is  -starshaped,
-starshaped,  (resp.,
(resp.,  ),
),  is compact (resp.,
is compact (resp.,  is weakly compact), and
is weakly compact), and  is continuous on
is continuous on  (resp.,
(resp.,  is demiclosed at
is demiclosed at  ). If the following condition holds:
). If the following condition holds:

for all  then
then  .
.
Theorem 2.20.
Let  ,
,  ,
,  be self-mappings of a Banach space
be self-mappings of a Banach space  with
with  and
and  such that
such that  . Suppose that
. Suppose that  ,
,  ,
,  for all
for all  , and
, and  is compact. Then one has the following:
is compact. Then one has the following:
(1) is nonempty closed and convex,
is nonempty closed and convex,
(2) ,
,
(3) provided
provided  is continuous,
is continuous,  is
is  -starshaped,
-starshaped,  , and the pair
, and the pair  satisfies the inequality (2.5) for all
satisfies the inequality (2.5) for all  is
is  -starshaped with
-starshaped with  ,
,  , and the inequality (2.16) holds for all
, and the inequality (2.16) holds for all  and
and  .
.
Proof.
-
(1)
and (2) follow from [5, 8]. By (2), the compactness of
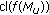 implies that
implies that 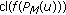 and
and 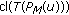 is compact. Theorem 2.7 implies that
is compact. Theorem 2.7 implies that  . Further,
. Further,  is
is 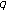 -starshaped with
-starshaped with 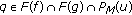 . Therefore, the conclusion now follows from Theorem 2.19 applied to
. Therefore, the conclusion now follows from Theorem 2.19 applied to  .
.
Remark 2.21.
-
(1)
Theorem 2.20 extends [13, Theorem 4.1], [10, Theorem 8], [5, Theorem 2.13], [8, Theorem 2.14], and [14, Theorem 2.11].
-
(2)
Theorems 2.7–2.16 represent very strong variants of the results in [3, 8, 11, 13] in the sense that the commutativity or compatibility of the mappings
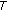 and
and 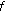 is replaced by the hypothesis that
is replaced by the hypothesis that 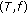 is a Banach operator pair,
is a Banach operator pair,  needs not be linear or affine, and
needs not be linear or affine, and 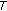 needs not be
needs not be 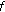 -nonexpansive.
-nonexpansive. -
(3)
The Banach operator pairs are different from those of weakly compatible,
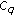 -commuting and
-commuting and 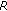 -subweakly commuting mappings and so our results are different from those in [3, 7, 8, 17]. Consider
-subweakly commuting mappings and so our results are different from those in [3, 7, 8, 17]. Consider  with the norm
with the norm 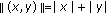 for all
for all  . Define two self-mappings
. Define two self-mappings 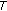 and
and 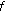 on
on 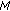 as follows:
as follows:  (2.17)
(2.17)
Then we have the following:

Thus  is a Banach operator pair. It is easy to see that
is a Banach operator pair. It is easy to see that  is
is  -weak contraction and
-weak contraction and  ,
,  do not commute on the set
do not commute on the set  , and so are not weakly compatible. Clearly,
, and so are not weakly compatible. Clearly,  is not affine or linear,
is not affine or linear,  is convex and
is convex and  is a common fixed point of
is a common fixed point of  and
and  .
.
References
Jungck G: Commuting mappings and fixed points. The American Mathematical Monthly 1976,83(4):261–263. 10.2307/2318216
Jungck G: Common fixed points for commuting and compatible maps on compacta. Proceedings of the American Mathematical Society 1988,103(3):977–983. 10.1090/S0002-9939-1988-0947693-2
Jungck G, Hussain N: Compatible maps and invariant approximations. Journal of Mathematical Analysis and Applications 2007,325(2):1003–1012. 10.1016/j.jmaa.2006.02.058
Chen J, Li Z: Common fixed-points for Banach operator pairs in best approximation. Journal of Mathematical Analysis and Applications 2007,336(2):1466–1475. 10.1016/j.jmaa.2007.01.064
Hussain N: Common fixed points in best approximation for Banach operator pairs with Ćirić type -contractions. Journal of Mathematical Analysis and Applications 2008,338(2):1351–1363. 10.1016/j.jmaa.2007.06.008
Hussain N, Rhoades BE: -commuting maps and invariant approximations. Fixed Point Theory and Applications 2006, 2006:-9.
O'Regan D, Hussain N: Generalized -contractions and pointwise -subweakly commuting maps. Acta Mathematica Sinica 2007,23(8):1505–1508. 10.1007/s10114-007-0935-7
Hussain N, Jungck G: Common fixed point and invariant approximation results for noncommuting generalized -nonexpansive maps. Journal of Mathematical Analysis and Applications 2006,321(2):851–861. 10.1016/j.jmaa.2005.08.045
Meinardus G: Invarianz bei linearen approximationen. Archive for Rational Mechanics and Analysis 1963, 14: 301–303.
Habiniak L: Fixed point theorems and invariant approximations. Journal of Approximation Theory 1989,56(3):241–244. 10.1016/0021-9045(89)90113-5
Jungck G, Sessa S: Fixed point theorems in best approximation theory. Mathematica Japonica 1995,42(2):249–252.
Singh SP: An application of a fixed-point theorem to approximation theory. Journal of Approximation Theory 1979,25(1):89–90. 10.1016/0021-9045(79)90036-4
Al-Thagafi MA: Common fixed points and best approximation. Journal of Approximation Theory 1996,85(3):318–323. 10.1006/jath.1996.0045
Pathak HK, Hussain N: Common fixed points for Banach operator pairs with applications. Nonlinear Analysis: Theory, Methods & Applications 2008,69(9):2788–2802. 10.1016/j.na.2007.08.051
Pathak HK, Cho YJ, Kang SM: An application of fixed point theorems in best approximation theory. International Journal of Mathematics and Mathematical Sciences 1998,21(3):467–470. 10.1155/S0161171298000659
Khan AR, Akbar F: Common fixed points from best simultaneous approximations. Taiwanese Journal of Mathematics 2009., 13:
Al-Thagafi MA, Shahzad N: Banach operator pairs, common fixed-points, invariant approximations, and -nonexpansive multimaps. Nonlinear Analysis: Theory, Methods & Applications 2008,69(8):2733–2739. 10.1016/j.na.2007.08.047
Berinde V: On the approximation of fixed points of weak contractive mappings. Carpathian Journal of Mathematics 2003,19(1):7–22.
Berinde V: Iterative Approximation of Fixed Points, Lecture Notes in Mathematics. Volume 1912. 2nd edition. Springer, Berlin, Germany; 2007:xvi+322.
Khamsi MA, Kirk WA: An Introduction to Metric Spaces and Fixed Point Theory, Pure and Applied Mathematics. Wiley-Interscience, New York, NY, USA; 2001:x+302.
Berinde V: Approximating fixed points of weak contractions using the Picard iteration. Nonlinear Analysis Forum 2004,9(1):43–53.
Berinde V, Păcurar M: Fixed points and continuity of almost contractions. Fixed Point Theory 2008,9(1):23–34.
Singh SP, Watson B, Srivastava P: Fixed Point Theory and Best Approximation: The KKM-Map Principle, Mathematics and Its Applications. Volume 424. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1997.
Ćirić LB: A generalization of Banach's contraction principle. Proceedings of the American Mathematical Society 1974,45(2):267–273.
Ćirić LB: Contractive type non-self mappings on metric spaces of hyperbolic type. Journal of Mathematical Analysis and Applications 2006,317(1):28–42. 10.1016/j.jmaa.2005.11.025
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hussain, N., Cho, Y.J. Weak Contractions, Common Fixed Points, and Invariant Approximations. J Inequal Appl 2009, 390634 (2009). https://doi.org/10.1155/2009/390634
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/390634
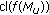 implies that
implies that 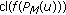 and
and 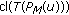 is compact. Theorem 2.7 implies that
is compact. Theorem 2.7 implies that  . Further,
. Further,  is
is 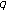 -starshaped with
-starshaped with 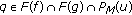 . Therefore, the conclusion now follows from Theorem 2.19 applied to
. Therefore, the conclusion now follows from Theorem 2.19 applied to  .
.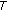 and
and 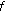 is replaced by the hypothesis that
is replaced by the hypothesis that 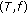 is a Banach operator pair,
is a Banach operator pair,  needs not be linear or affine, and
needs not be linear or affine, and 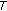 needs not be
needs not be 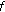 -nonexpansive.
-nonexpansive.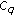 -commuting and
-commuting and 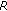 -subweakly commuting mappings and so our results are different from those in [
-subweakly commuting mappings and so our results are different from those in [ with the norm
with the norm 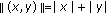 for all
for all  . Define two self-mappings
. Define two self-mappings 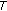 and
and 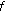 on
on 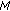 as follows:
as follows: 