- Research Article
- Open access
- Published:
On the Generalized 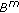 -Riesz Difference Sequence Space and
-Riesz Difference Sequence Space and  -Property
-Property
Journal of Inequalities and Applications volume 2009, Article number: 385029 (2009)
Abstract
We introduce the generalized Riesz difference sequence space  which is defined by
which is defined by  where
where  is the Riesz sequence space defined by Altay and Başar. We give some topological properties, compute the
is the Riesz sequence space defined by Altay and Başar. We give some topological properties, compute the  duals, and determine the Schauder basis of this space. Finally; we study the characterization of some matrix mappings on this sequence space. At the end of the paper, we investigate some geometric properties of
duals, and determine the Schauder basis of this space. Finally; we study the characterization of some matrix mappings on this sequence space. At the end of the paper, we investigate some geometric properties of  and we have proved that this sequence space has property
and we have proved that this sequence space has property  for
for  .
.
1. Introduction
Let  be the space of all real valued sequences. We write
be the space of all real valued sequences. We write  for the sequence spaces of all bounded, convergent, and null sequences, respectively. Also by
for the sequence spaces of all bounded, convergent, and null sequences, respectively. Also by  ,
,  , and
, and  , we denote the sequence spaces of all convergent, absolutely and
, we denote the sequence spaces of all convergent, absolutely and  -absolutely, convergent series, respectively; where
-absolutely, convergent series, respectively; where 
Let  be a sequence of positive numbers and
be a sequence of positive numbers and

Then the matrix  of the Riesz mean
of the Riesz mean  , which is triangle limitation matrix, is given by
, which is triangle limitation matrix, is given by

It is well known that the matrix  is regular if and only if
is regular if and only if  as
as 
Altay and Başar [1, 2] introduced the Riesz sequence space  , and
, and  of nonabsolute type which is the set of all sequences whose
of nonabsolute type which is the set of all sequences whose  -transforms are in the space
-transforms are in the space  , and
, and  respectively. Here and afterwards,
respectively. Here and afterwards,  will be used as a bounded sequence of strictly positive real numbers with
will be used as a bounded sequence of strictly positive real numbers with  and
and  and
and  denotes the collection of all finite subsets of
denotes the collection of all finite subsets of  where
where  . The Riesz sequence space introduced in [1] by Altay and Başar is
. The Riesz sequence space introduced in [1] by Altay and Başar is

The difference sequence spaces  , and
, and  were first defined and studied by Kızmaz in [3] and studied by several authors, [4–9]. Başar and Altay [10] have studied the sequence space
were first defined and studied by Kızmaz in [3] and studied by several authors, [4–9]. Başar and Altay [10] have studied the sequence space  as the set of all sequences such that their
as the set of all sequences such that their  -transforms are in the space
-transforms are in the space  ; that is,
; that is,

where  denotes the matrix
denotes the matrix  defined by
defined by

The idea of difference sequences is generalized by Çolak and Et [11]. They defined the sequence spaces:

where  , and
, and  , where
, where  denotes the matrix
denotes the matrix  defined by
defined by

for all  and for any fixed
and for any fixed  .
.
Recently, Başarir and Öztürk [12] introduced the Riesz difference sequence space as follows:

Başar and Altay defined the matrix  which generalizes the matrix
which generalizes the matrix  . Now we define the matrix
. Now we define the matrix  and if we take
and if we take  , then it corresponds to the matrix
, then it corresponds to the matrix  . We define
. We define

The results related to the matrix domain of the matrix  are more general and more comprehensive than the corresponding consequences of matrix domain of
are more general and more comprehensive than the corresponding consequences of matrix domain of 
Our main subject in the present paper is to introduce the generalized Riesz difference sequence space  which consists of all the sequences such that their
which consists of all the sequences such that their  -transforms are in the space
-transforms are in the space  and to investigate some topological and geometric properties with respect to paranorm on this space.
and to investigate some topological and geometric properties with respect to paranorm on this space.
2. Basic Facts and Definitions
In this section we give some definitions and lemmas which will be frequently used.
Definition 2.1.
Let  and
and  be two sequence spaces and let
be two sequence spaces and let  be an infinite matrix of real numbers
be an infinite matrix of real numbers  where
where  . Then, we say that
. Then, we say that  defines a matrix mapping from
defines a matrix mapping from  into
into  and we denote it by writing
and we denote it by writing  if for every sequence
if for every sequence  the sequence
the sequence  the
the  -transform of
-transform of  is in
is in  where
where

By  we denote the class of all matrices
we denote the class of all matrices  such that
such that  Thus,
Thus,  if and only if the series on the right side of (2.1) converges for each
if and only if the series on the right side of (2.1) converges for each  and every
and every  and we have
and we have  for all
for all  A sequence
A sequence  is said to be
is said to be  -summable to
-summable to  if
if  converges to
converges to  which is called as the
which is called as the  -limit of
-limit of 
Definition 2.2.
For any sequence space  the matrix domain
the matrix domain  of an infinite matrix
of an infinite matrix  is defined by
is defined by

Definition 2.3.
If a sequence space  paranormed by
paranormed by  contains a sequence
contains a sequence  with the property that for every
with the property that for every  there is a unique sequence of scalars
there is a unique sequence of scalars  such that
such that

then  is called a Schauder basis (or briefly basis) for
is called a Schauder basis (or briefly basis) for  . The series
. The series  which has the sum
which has the sum  is then called the expansion of
is then called the expansion of  with respect to
with respect to  and is written as
and is written as 
Definition 2.4.
For the sequence spaces  and
and  , define the set
, define the set  by
by

With the notation of (2.2), the  -
- -
- -duals of a sequence space
-duals of a sequence space  which are, respectively, denoted by
which are, respectively, denoted by  are defined by
are defined by

Now we give some lemmas which we need to prove our theorems.
Lemma 2.5 (see [13]).
( i) Let  for every
for every  Then
Then  if and only if there exists an integer
if and only if there exists an integer  such that
such that

( ii) Let  for every
for every  Then
Then  if and only if
if and only if

Lemma 2.6 (see [14]).
( i) Let  for every
for every  Then
Then  if and only if there exists an integer
if and only if there exists an integer  such that
such that

( ii) Let  for every
for every  Then
Then  if and only if
if and only if

Lemma 2.7 (see [14]).
Let  for every
for every  Then
Then  if and only if (2.8), (2.9) hold, and
if and only if (2.8), (2.9) hold, and

also holds.
3. Some Topological Properties of Generalized  -RieszDifference Sequence Space
-RieszDifference Sequence Space
Let us define the sequence  which will be used for the
which will be used for the  -transform of a sequence
-transform of a sequence  , that is,
, that is,

After this, by  we denote the matrix
we denote the matrix  defined by
defined by

for all  Then we define
Then we define

If we take  then we have
then we have

Here are some topological properties of the generalized Riesz difference sequence space.
Theorem 3.1.
The sequence space  is a complete linear metric space paranormed by
is a complete linear metric space paranormed by

where  and
and 
Proof.
The linearity of  with respect to the co-ordinatewise addition and scalar multiplication follows from the inequalites which are satisfied for
with respect to the co-ordinatewise addition and scalar multiplication follows from the inequalites which are satisfied for  [15]:
[15]:

and for any  [16], we have
[16], we have

It is obvious that  and
and  for all
for all  . Let
. Let  :
:


Again the inequalities (3.7) and (3.9) yield the subadditivity of  and
and

Let  be any sequence of the elements of the space
be any sequence of the elements of the space  such that
such that

and  also be any sequence of scalars such that
also be any sequence of scalars such that  Then, since the inequality
Then, since the inequality

holds by subadditivity of  is bounded, and thus we have
is bounded, and thus we have

which tends to zero as  Hence the continuity of the scalar multiplication has shown. Finally; it is clear to say that
Hence the continuity of the scalar multiplication has shown. Finally; it is clear to say that  is a paranorm on the space
is a paranorm on the space 
Moreover; we will prove the completeness of the space  Let
Let  be any Cauchy sequence in the space
be any Cauchy sequence in the space  where
where  Then, for a given
Then, for a given  there exists a positive integer
there exists a positive integer  such that
such that

for all  If we use the definition of
If we use the definition of  , we obtain for each fixed
, we obtain for each fixed  that
that

for  which leads us to the fact that
which leads us to the fact that

is a Cauchy sequence of real numbers for every fixed  Since
Since  is complete, it converges, so we write
is complete, it converges, so we write  as
as  Hence by using these infinitely many limits
Hence by using these infinitely many limits  , we define the sequence
, we define the sequence  . Since (3.14) holds for each
. Since (3.14) holds for each  and
and 

Take any  first let
first let  in (3.17) and then
in (3.17) and then  to obtain
to obtain  Finally, taking
Finally, taking  in (3.17) and letting
in (3.17) and letting  we have Minkowski's inequality for each
we have Minkowski's inequality for each  , that is,
, that is,

which implies that  . Since
. Since  for all
for all  it follows that
it follows that  as
as  so
so  is complete.
is complete.
Theorem 3.2.
Let  for each
for each  Then the difference sequence space
Then the difference sequence space  is linearly isomorphic to the space
is linearly isomorphic to the space  where
where 
Proof.
For the proof of the theorem, we should show the existence of a linear bijection between the spaces  and
and  for
for  With the notation of
With the notation of

define the transformation  from
from  to
to  by
by  . However,
. However,  is a linear transformation, moreover; it is obviuos that
is a linear transformation, moreover; it is obviuos that  whenever
whenever  and hence
and hence  is injective.
is injective.
Let  and define the sequence
and define the sequence  by
by

Then,

where

and  is a paranorm on
is a paranorm on  . Thus, we have that
. Thus, we have that  Consequently;
Consequently;  is surjective and is paranorm preserving. Hence,
is surjective and is paranorm preserving. Hence,  is a linear bijection and this explains that the spaces
is a linear bijection and this explains that the spaces  and
and  are linearly isomorphic.
are linearly isomorphic.
Now, the Schauder basis for the space  will be given in the following theorem.
will be given in the following theorem.
Theorem 3.3.
Define the sequence  of the elements of the space
of the elements of the space  for every fixed
for every fixed  by
by

Then; the sequence  is a basis for the space
is a basis for the space  and any
and any  has a unique representation of the form
has a unique representation of the form

where  for all
for all  and
and 
Proof.
This can be easily obtained by [12, Theorem 5] so we omit the proof.
Theorem 3.4.
( i) Let  for every
for every  Define the set
Define the set  as follows:
as follows:

Then; 
( ii) Let  for every
for every  Define the set
Define the set  by
by

Then; 
Proof.

Let  We easily derive with the notation
We easily derive with the notation

and the matrix  which is defined by
which is defined by

for all  , thus, by using the method in [1], [12] we deduce that
, thus, by using the method in [1], [12] we deduce that  whenever
whenever  if and only if
if and only if  whenever
whenever  From Lemma 2.5(i), we obtain the desired result that
From Lemma 2.5(i), we obtain the desired result that


This is easily obtained by proceeding as in the proof of (i), above by using the second part of Lemma 2.5. So we omit the detail.
Theorem 3.5.
( i) Let  for every
for every  Define the set
Define the set  as follow:
as follow:

Then; 
( ii) Let  for every
for every  Define the set
Define the set  by
by

Then; 
Proof.

If we take the matrix  by
by

for  and if we carry out the method which is used in [1, 12], we get that
and if we carry out the method which is used in [1, 12], we get that  whenever
whenever  if and only if
if and only if  whenever
whenever  Hence we deduce from Lemma 2.7 that
Hence we deduce from Lemma 2.7 that

and  exists
exists which is shown that
which is shown that


This may be obtained in the similar way as in the proof of (i) above by using the second part of Lemmas 2.6 and 2.7. So we omit the detail.
Now we will characterize the matrix mappings from the space  to the space
to the space  . It can be proved by applying the method in [1, 12]. So we omit the proof.
. It can be proved by applying the method in [1, 12]. So we omit the proof.
Theorem 3.6.
( i) Let  for every
for every  Then
Then  if and only if there exists an integer
if and only if there exists an integer  such that
such that

for each 
( ii) Let  for every
for every  Then
Then  if and only if
if and only if

for each 
4.  -Property of Generalized Riesz Difference Sequence Space
-Property of Generalized Riesz Difference Sequence Space
In the previous section; we show that the sequence space  which is the space of all real sequences
which is the space of all real sequences  such that
such that  is a complete paranormed space. It is paranormed by
is a complete paranormed space. It is paranormed by  for all
for all  where
where  We recall that a paranormed space is total if
We recall that a paranormed space is total if  implies
implies  Every total paranormed space becomes a linear metric space with the metric given by
Every total paranormed space becomes a linear metric space with the metric given by  It is clear that
It is clear that  is a total paranormed space.
is a total paranormed space.
In this section, we investigate some geometric properties of  . First we give the definition of the property
. First we give the definition of the property  in a paranormed space and we will use the method in [17] to prove the property
in a paranormed space and we will use the method in [17] to prove the property  Consequently, we obtain that
Consequently, we obtain that  has property
has property  for
for 
From here, for a sequence  and for
and for  , we use the notation
, we use the notation  and
and  .
.
Now we give the definition of the property  in a linear metric space.
in a linear metric space.
Definition 4.1.
A linear metric space  is said to have the property
is said to have the property  if for each
if for each  and
and  there exists
there exists  such that for each element
such that for each element  and each sequence
and each sequence  in
in  with
with  for all
for all  there is an index
there is an index  for which
for which 
Lemma 4.2.
If  then for any
then for any  and
and  and for any
and for any  there exists
there exists  such that
such that

whenever  and
and 
Proof.
Let  and
and  be given. Let
be given. Let  and
and  , there exists
, there exists  such that
such that  for all
for all  Let
Let  Thus
Thus  for all
for all  . There exists
. There exists  such that
such that

for all  Set
Set  There exists
There exists  such that
such that

for all  Set
Set  Assume that
Assume that  and
and  We recall that
We recall that  and
and  . With these notations, let
. With these notations, let  and
and  By using convexity of the function
By using convexity of the function  for all
for all  and the fact that
and the fact that  for
for  and
and  where
where  and
and  , we have
, we have

Lemma 4.3.
If  then for any
then for any  there exists
there exists  and
and  such that
such that

for all  with
with 
Proof.
Let  be a real number such that
be a real number such that  Then there exists
Then there exists  such that
such that  for all
for all  Let
Let  be a real number such that
be a real number such that  Then for each
Then for each  and
and  we have
we have

Theorem 4.4.
If  then
then  has property
has property 
Proof.
Let  and
and  with
with  for
for  Take
Take  There exists
There exists  such that
such that  Let
Let  Since for each
Since for each  is bounded, by using the diagonal method, we have that for each
is bounded, by using the diagonal method, we have that for each  , we can find a subsequence
, we can find a subsequence  of
of  such that
such that  converges for all
converges for all  with
with  Since
Since  is Cauchy sequence for all
is Cauchy sequence for all  there exists
there exists  such that
such that

for all  Then we see that
Then we see that

Therefore, for each  there exists
there exists  such that
such that

for all  Hence, there is a sequence of positive integers
Hence, there is a sequence of positive integers  with
with  such that
such that

for all  By Lemma 4.3, there exists
By Lemma 4.3, there exists  and
and  such that
such that

for all  and
and  Let
Let  be a real number corresponding to Lemma 4.2 with
be a real number corresponding to Lemma 4.2 with

and  that is
that is

whenever  and
and  Since
Since  we have that
we have that  . Let
. Let  be such that
be such that

Put  and
and  Then
Then

Hence;


By using (4.17) and convexity of the function  , we have
, we have

Hence  So this implies that
So this implies that

for some  Finally; we can say that the sequence space
Finally; we can say that the sequence space  has property
has property 
References
Altay B, Başar F: On the paranormed Riesz sequence spaces of non-absolute type. Southeast Asian Bulletin of Mathematics 2003,26(5):701–715.
Altay B, Başar F: Some Euler sequence spaces of nonabsolute type. Ukrainian Mathematical Journal 2005,57(1):1–17. 10.1007/s11253-005-0168-9
Kızmaz H: On certain sequence spaces. Canadian Mathematical Bulletin 1981,24(2):169–176. 10.4153/CMB-1981-027-5
Altay B, Polat H: On some new Euler difference sequence spaces. Southeast Asian Bulletin of Mathematics 2006,30(2):209–220.
Polat H, Başar F: Some Euler spaces of difference sequences of order . Acta Mathematica Scientia. Series B 2007,27(2):254–266. 10.1016/S0252-9602(07)60024-1
Malkowsky E, Parashar SD: Matrix transformations in spaces of bounded and convergent difference sequences of order . Analysis 1997,17(1):87–97.
Et M, Başarir M: On some new generalized difference sequence spaces. Periodica Mathematica Hungarica 1997,35(3):169–175. 10.1023/A:1004597132128
Başarir M, Nuray F: Paranormed difference sequence spaces generated by infinite matrices. Pure and Applied Mathematika Sciences 1991,34(1–2):87–90.
Polat H, Başarir M: New Taylor difference sequence spaces of order . International Mathematical Journal 2004,5(3):211–223.
Başar F, Altay B: On the space of sequences of -bounded variation and related matrix mappings. Ukrainian Mathematical Journal 2003,55(1):136–147. 10.1023/A:1025080820961
Çolak R, Et M: On some generalized difference sequence spaces and related matrix transformations. Hokkaido Mathematical Journal 1997,26(3):483–492.
Başarir M, Öztürk M: On the Riesz difference sequence space. Rendiconti del Circolo Matematico di Palermo 2008,57(3):377–389. 10.1007/s12215-008-0027-2
Grosse-Erdmann K-G: Matrix transformations between the sequence spaces of Maddox. Journal of Mathematical Analysis and Applications 1993,180(1):223–238. 10.1006/jmaa.1993.1398
Lascarides CG, Maddox IJ: Matrix transformations between some classes of sequences. Proceedings of the Cambridge Philosophical Society 1970, 68: 99–104. 10.1017/S0305004100001109
Maddox IJ: Elements of Functional Analysis. Cambridge University Press, Cambridge, UK; 1970:x+208.
Maddox IJ: Paranormed sequence spaces generated by infinite matrices. Proceedings of the Cambridge Philosophical Society 1968, 64: 335–340. 10.1017/S0305004100042894
Khompurngson K: Geometric properties of some paranormed sequence spaces, M.S. thesis. Chiang Mai University, Chiang Mai, Thailand; 2004.
Acknowledgment
We would like to express our gratitude to the reviewer for his/her careful reading and valuable suggestions which improved the presentation of the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Başarir, M., Kayikçi, M. On the Generalized 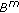 -Riesz Difference Sequence Space and
-Riesz Difference Sequence Space and  -Property.
J Inequal Appl 2009, 385029 (2009). https://doi.org/10.1155/2009/385029
-Property.
J Inequal Appl 2009, 385029 (2009). https://doi.org/10.1155/2009/385029
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/385029
 -RieszDifference Sequence Space
-RieszDifference Sequence Space -Property of Generalized Riesz Difference Sequence Space
-Property of Generalized Riesz Difference Sequence Space