- Research Article
- Open access
- Published:
Moment Inequality for  -Mixing Sequences and Its Applications
-Mixing Sequences and Its Applications
Journal of Inequalities and Applications volume 2009, Article number: 379743 (2009)
Abstract
Firstly, the maximal inequality for  -mixing sequences is given. By using the maximal inequality, we study the convergence properties for
-mixing sequences is given. By using the maximal inequality, we study the convergence properties for  -mixing sequences. The Hájek-Rényi-type inequality, strong law of large numbers, strong growth rate and the integrability of supremum for
-mixing sequences. The Hájek-Rényi-type inequality, strong law of large numbers, strong growth rate and the integrability of supremum for  -mixing sequences are obtained.
-mixing sequences are obtained.
1. Introduction
Let  be a random variable sequence defined on a fixed probability space
be a random variable sequence defined on a fixed probability space  and
and  for each
for each  . Let
. Let  and
and  be positive integers. Write
be positive integers. Write  . Given
. Given  -algebras
-algebras  ,
,  in
in  , let
, let

Define the  -mixing coefficients by
-mixing coefficients by

Definition 1.1.
A random variable sequence  is said to be a
is said to be a  -mixing random variable sequence if
-mixing random variable sequence if  as
as  .
.
The concept of  -mixing random variables was introduced by Dobrushin [1] and many applications have been found. See, for example, Dobrushin [1], Utev [2], and Chen [3] for central limit theorem, Herrndorf [4] and Peligrad [5] for weak invariance principle, Sen [6, 7] for weak convergence of empirical processes, Iosifescu [8] for limit theorem, Peligrad [9] for Ibragimov-Iosifescu conjecture, Shao [10] for almost sure invariance principles, Hu and Wang [11] for large deviations, and so forth. When these are compared with the corresponding results of independent random variable sequences, there still remains much to be desired. The main purpose of this paper is to study the maximal inequality for
-mixing random variables was introduced by Dobrushin [1] and many applications have been found. See, for example, Dobrushin [1], Utev [2], and Chen [3] for central limit theorem, Herrndorf [4] and Peligrad [5] for weak invariance principle, Sen [6, 7] for weak convergence of empirical processes, Iosifescu [8] for limit theorem, Peligrad [9] for Ibragimov-Iosifescu conjecture, Shao [10] for almost sure invariance principles, Hu and Wang [11] for large deviations, and so forth. When these are compared with the corresponding results of independent random variable sequences, there still remains much to be desired. The main purpose of this paper is to study the maximal inequality for  -mixing sequences, by which we can get the Hájek-Rényi-type inequality, strong law of large numbers, strong growth rate, and the integrability of supremum for
-mixing sequences, by which we can get the Hájek-Rényi-type inequality, strong law of large numbers, strong growth rate, and the integrability of supremum for  -mixing sequences.
-mixing sequences.
Throughout the paper,  denotes a positive constant which may be different in various places. The main results of this paper depend on the following lemmas.
denotes a positive constant which may be different in various places. The main results of this paper depend on the following lemmas.
Lemma 1.2 (see Lu and Lin [12]).
Let  be a sequence of
be a sequence of  -mixing random variables. Let
-mixing random variables. Let  ,
,  ,
,  ,
,  and
and  . Then
. Then

Lemma 1.3 (see Shao [10]).
Let  be a
be a  -mixing sequence. Put
-mixing sequence. Put  . Suppose that there exists an array
. Suppose that there exists an array  of positive numbers such that
of positive numbers such that

Then for every  , there exists a constant
, there exists a constant  depending only on
depending only on  and
and  such that
such that

for every  and
and  .
.
Lemma 1.4 (see Hu et al. [13]).
Let  be a nondecreasing unbounded sequence of positive numbers and let
be a nondecreasing unbounded sequence of positive numbers and let  be nonnegative numbers. Let
be nonnegative numbers. Let  and
and  be fixed positive numbers. Assume that for each
be fixed positive numbers. Assume that for each  ,
,


then

and with the growth rate

where

If further we assume that  for infinitely many
for infinitely many  , then
, then

Lemma 1.5 (see Fazekas and Klesov [14] and Hu [15]).
Let  be a nondecreasing unbounded sequence of positive numbers and let
be a nondecreasing unbounded sequence of positive numbers and let  be nonnegative numbers. Denote
be nonnegative numbers. Denote  for
for  . Let
. Let  be a fixed positive number satisfying (1.6). If
be a fixed positive number satisfying (1.6). If


then (1.8)–(1.11) hold.
2. Maximal Inequality for 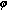 -Mixing Sequences
-Mixing Sequences
Theorem 2.1.
Let  be a sequence of
be a sequence of  -mixing random variables satisfying
-mixing random variables satisfying  . Assume that
. Assume that  and
and  for each
for each  . Then there exists a constant
. Then there exists a constant  depending only on
depending only on  such that for any
such that for any  and
and 


In particular,


where  may be different in various places.
may be different in various places.
Proof.
By Lemma 1.2 for  , we can see that
, we can see that

which implies (2.1). By (2.1) and Lemma 1.3 (take  ), we can get
), we can get

The proof is completed.
3. Hájek-Rényi-Type Inequality for  -Mixing Sequences
-Mixing Sequences
In this section, we will give the Hájek-Rényi-type inequality for  -mixing sequences, which can be applied to obtain the strong law of large numbers and the integrability of supremum.
-mixing sequences, which can be applied to obtain the strong law of large numbers and the integrability of supremum.
Theorem 3.1.
Let  be a sequence of
be a sequence of  -mixing random variables satisfying
-mixing random variables satisfying  and let
and let  be a nondecreasing sequence of positive numbers. Then for any
be a nondecreasing sequence of positive numbers. Then for any  and any integer
and any integer  ,
,

where  is defined in (2.4) in Theorem 2.1.
is defined in (2.4) in Theorem 2.1.
Proof.
Without loss of generality, we assume that  for all
for all  . Let
. Let  . For
. For  , define
, define

For  , we let
, we let  and
and  be the index of the last nonempty set
be the index of the last nonempty set  . Obviously,
. Obviously,  if
if  and
and  . It is easily seen that
. It is easily seen that  if
if  and
and  is also a sequence of
is also a sequence of  -mixing random variables. By Markov's inequality and (2.4), we have
-mixing random variables. By Markov's inequality and (2.4), we have

Now we estimate  . Let
. Let  . Then
. Then  follows from the definition of
follows from the definition of  . Therefore,
. Therefore,

Thus, (3.1) follows from (3.3) and (3.4) immediately.
Theorem 3.2.
Let  be a sequence of
be a sequence of  -mixing random variables satisfying
-mixing random variables satisfying  and let
and let  be a nondecreasing sequence of positive numbers. Then for any
be a nondecreasing sequence of positive numbers. Then for any  and any positive integers
and any positive integers  ,
,

where  is defined in (3.1).
is defined in (3.1).
Proof.
Observe that

thus

For  , by Markov's inequality and (2.3), we have
, by Markov's inequality and (2.3), we have

For  , we will apply Theorem 3.1 to
, we will apply Theorem 3.1 to  and
and  . Noting that
. Noting that

thus, by Theorem 3.1, we get

Therefore, the desired result (3.5) follows from (3.7)–(3.10) immediately.
Theorem 3.3.
Let  be a sequence of
be a sequence of  -mixing random variables satisfying
-mixing random variables satisfying  and let
and let  be a nondecreasing sequence of positive numbers. Denote
be a nondecreasing sequence of positive numbers. Denote  for
for  . Assume that
. Assume that

then for any  ,
,

where  is defined in (3.1). Furthermore, if
is defined in (3.1). Furthermore, if  , then
, then

Proof.
By the continuity of probability and Theorem 3.1, we get

Observe that

By Theorem 3.2, we have that

Hence, by (3.11) and Kronecker's Lemma, it follows that

which is equivalent to

So the desired results are proved.
4. Strong Law of Large Numbers and Growth Rate for  -Mixing Sequences
-Mixing Sequences
Theorem 4.1.
Let  be a sequence of mean zero
be a sequence of mean zero  -mixing random variables satisfying
-mixing random variables satisfying  and let
and let  be a nondecreasing unbounded sequence of positive numbers. Assume that
be a nondecreasing unbounded sequence of positive numbers. Assume that

then

and with the growth rate

where


If further we assume that  for infinitely many
for infinitely many  , then
, then

Proof.
By (2.4) in Theorem 2.1, we have

It follows by (4.1) that

Thus, (4.2)–(4.6) follow from (4.7), (4.8), and Lemma 1.4 immediately. We complete the proof of the theorem.
Theorem 4.2.
Let  be a sequence of
be a sequence of  -mixing random variables with
-mixing random variables with  .
.  . Denote
. Denote 
 for
for  and
and  . Assume that
. Assume that

then

and with the growth rate

where



If further we assume that  for infinitely many
for infinitely many  , then
, then

In addition, for any  ,
,

Proof.
Assume that  ,
,  and
and  ,
,  . By (2.4) in Theorem 2.1, we can see that
. By (2.4) in Theorem 2.1, we can see that

It is a simple fact that  for all
for all  . It follows by (4.9) that
. It follows by (4.9) that

That is to say (1.12) holds. By Remark  in Fazekas and Klesov [14], (1.12) implies (1.13). By Lemma 1.5, we can obtain (4.10)–(4.15) immetiately. By (4.14), it follows that
in Fazekas and Klesov [14], (1.12) implies (1.13). By Lemma 1.5, we can obtain (4.10)–(4.15) immetiately. By (4.14), it follows that

The proof is completed.
Remark 4.3.
By using the maximal inequality, we get the Hájek-Rényi-type inequality, the strong law of large numbers and the strong growth rate for  -mixing sequences. In addition, we get some new bounds of probability inequalities for
-mixing sequences. In addition, we get some new bounds of probability inequalities for  -mixing sequences, such as (3.1), (3.5), (3.12), (4.5)–(4.6), and (4.13)–(4.16).
-mixing sequences, such as (3.1), (3.5), (3.12), (4.5)–(4.6), and (4.13)–(4.16).
References
Dobrushin RL: The central limit theorem for non-stationary Markov chain. Theory of Probability and Its Applications 1956,1(4):72–88.
Utev SA: On the central limit theorem for -mixing arrays of random variables. Theory of Probability and Its Applications 1990,35(1):131–139. 10.1137/1135013
Chen DC: A uniform central limit theorem for nonuniform -mixing random fields. The Annals of Probability 1991,19(2):636–649. 10.1214/aop/1176990445
Herrndorf N: The invariance principle for -mixing sequences. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete 1983,63(1):97–108. 10.1007/BF00534180
Peligrad M: An invariance principle for -mixing sequences. The Annals of Probability 1985,13(4):1304–1313. 10.1214/aop/1176992814
Sen PK: A note on weak convergence of empirical processes for sequences of -mixing random variables. Annals of Mathematical Statistics 1971,42(6):2131–2133. 10.1214/aoms/1177693079
Sen PK: Weak convergence of multidimensional empirical processes for stationary -mixing processes. The Annals of Probability 1974,2(1):147–154. 10.1214/aop/1176996760
Iosifescu J: Limit theorem for -mixing sequences. Proceedings of the 5th Conference on Probability Theory, September 1977 1–6.
Peligrad M: On Ibragimov-Iosifescu conjecture for -mixing sequences. Stochastic Processes and Their Applications 1990,35(2):293–308. 10.1016/0304-4149(90)90008-G
Shao QM: Almost sure invariance principles for mixing sequences of random variables. Stochastic Processes and Their Applications 1993,48(2):319–334. 10.1016/0304-4149(93)90051-5
Hu S, Wang X: Large deviations for some dependent sequences. Acta Mathematica Scientia. Series B 2008,28(2):295–300. 10.1016/S0252-9602(08)60030-2
Lu CR, Lin ZY: Limit Theory for Mixing Dependent Sequences. Science Press, Beijing, China; 1997.
Hu S, Chen G, Wang X: On extending the Brunk-Prokhorov strong law of large numbers for martingale differences. Statistics & Probability Letters 2008,78(18):3187–3194. 10.1016/j.spl.2008.06.017
Fazekas I, Klesov O: A general approach to the strong law of large numbers. Theory of Probability and Its Applications 2001,45(3):436–449. 10.1137/S0040585X97978385
Hu S: Some new results for the strong law of large numbers. Acta Mathematica Sinica 2003,46(6):1123–1134.
Acknowledgments
The authors are most grateful to the Editor Sever Silvestru Dragomir, the referee Professor Mihaly Bencze and an anonymous referee for careful reading of the manuscript and valuable suggestions and comments which helped to significantly improve an earlier version of this paper. This work was supported by the National Natural Science Foundation of China (Grant nos. 10871001, 60803059) and the Innovation Group Foundation of Anhui University.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xuejun, W., Shuhe, H., Yan, S. et al. Moment Inequality for  -Mixing Sequences and Its Applications.
J Inequal Appl 2009, 379743 (2009). https://doi.org/10.1155/2009/379743
-Mixing Sequences and Its Applications.
J Inequal Appl 2009, 379743 (2009). https://doi.org/10.1155/2009/379743
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/379743
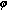 -Mixing Sequences
-Mixing Sequences -Mixing Sequences
-Mixing Sequences -Mixing Sequences
-Mixing Sequences