- Research Article
- Open access
- Published:
Generalized Lazarevic's Inequality and Its Applications—Part II
Journal of Inequalities and Applications volume 2009, Article number: 379142 (2009)
Abstract
A generalized Lazarevic's inequality is established. The applications of this generalized Lazarevic's inequality give some new lower bounds for logarithmic mean.
1. Introduction
Lazarević [1] (or see Mitrinović [2]) gives us the following result.
Theorem 1.1.
Let  . Then
. Then

holds if and only if  .
.
Recently, the author of this paper gives a new proof of the inequality (1.1) in [3] and extends the inequality (1.1) to the following result in [4].
Theorem 1.2.
Let  , and
, and  . Then
. Then

holds if and only if  .
.
Moreover, the inequality (1.1) can be extended as follows.
Theorem 1.3.
Let  or
or  , and
, and  . Then
. Then

holds if and only if  .
.
2. Three Lemmas
Let  be two continuous functions which are differentiable on
be two continuous functions which are differentiable on  . Further, let
. Further, let  on
on  . If
. If  is increasing (or decreasing) on
is increasing (or decreasing) on  , then the functions
, then the functions  and
and  are also increasing (or decreasing) on
are also increasing (or decreasing) on  .
.
Let  and
and  be real numbers, and let the power series
be real numbers, and let the power series  and
and  be convergent for
be convergent for  . If
. If  for
for  and if
and if  is strictly increasing (or decreasing) for
is strictly increasing (or decreasing) for  then the function
then the function  is strictly increasing (or decreasing) on
is strictly increasing (or decreasing) on  .
.
Lemma 2.3.
Let  and
and  . Then the function
. Then the function  strictly increases as
strictly increases as  increases.
increases.
3. A Concise Proof of Theorem 1.3
Let  , where
, where  , and
, and  . Then
. Then

where  , and
, and  .
.
We compute

where

and  .
.
We obtain results in two cases.
-
(a)
Let
 , then
, then 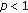 and
and 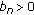 . Let
. Let  for
for  we have that
we have that 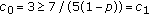 and
and 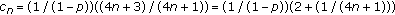 is decreasing for
is decreasing for 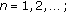 so
so  is decreasing for
is decreasing for  and
and  is decreasing on
is decreasing on  by Lemma 2.2. Hence
by Lemma 2.2. Hence 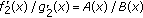 is decreasing on
is decreasing on 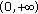 and
and  is decreasing on
is decreasing on  by Lemma 2.1. Thus
by Lemma 2.1. Thus 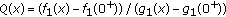 is decreasing on
is decreasing on  by Lemma 2.1.
by Lemma 2.1. -
(b)
Let
 , then
, then 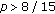 . Let
. Let 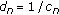 for
for  we have that
we have that 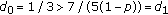 and
and  is decreasing for
is decreasing for  so
so  is decreasing for
is decreasing for  and
and  is decreasing on
is decreasing on  by Lemma 2.2. Hence
by Lemma 2.2. Hence 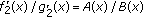 is increasing on
is increasing on 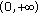 and
and 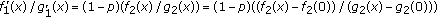 is decreasing on
is decreasing on 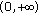 by Lemma 2.1. Thus
by Lemma 2.1. Thus 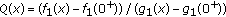 is decreasing on
is decreasing on 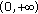 by Lemma 2.1.
by Lemma 2.1.
Since

the proof of Theorem 1.3 is complete.
4. Some New Lower Bounds for Logarithmic Mean
Assuming that  and
and  are two different positive numbers, let
are two different positive numbers, let  ,
,  , and
, and  be the arithmetic, geometric, and logarithmic means, respectively. It is well known that (see [2, 12–16])
be the arithmetic, geometric, and logarithmic means, respectively. It is well known that (see [2, 12–16])

Ostle and Terwilliger [17] (or see Leach and Sholander [18], Zhu [16]) gave bounds for  in terms of
in terms of  and
and  as follows:
as follows:

Without loss of generality, let  and
and  , then
, then  . Replacing
. Replacing  with
with  in (1.3), we obtain the following new results for three classical means.
in (1.3), we obtain the following new results for three classical means.
Theorem 4.1.
Let  or
or  , and
, and  and
and  be two positive numbers such that
be two positive numbers such that  . Then
. Then

holds if and only if  .
.
Now letting  in inequality (4.3) be
in inequality (4.3) be  , and
, and  , respectively, by Theorem 4.1 and Lemma 2.3 we have the following inequalities:
, respectively, by Theorem 4.1 and Lemma 2.3 we have the following inequalities:

References
Lazarević I: Neke nejednakosti sa hiperbolickim funkcijama. Univerzitet u Beogradu. Publikacije Elektrotehničkog Fakulteta. Serija Matematika i Fizika 1966, 170: 41–48.
Mitrinović DS: Analytic Inequalities. Springer, New York, NY, USA; 1970:xii+400.
Zhu L: On Wilker-type inequalities. Mathematical Inequalities & Applications 2007,10(4):727–731.
Zhu L: Generalized Lazarevic's inequality and its applications—part I. submitted submitted
Vamanamurthy MK, Vuorinen M: Inequalities for means. Journal of Mathematical Analysis and Applications 1994,183(1):155–166. 10.1006/jmaa.1994.1137
Anderson GD, Qiu S-L, Vamanamurthy MK, Vuorinen M: Generalized elliptic integrals and modular equations. Pacific Journal of Mathematics 2000,192(1):1–37. 10.2140/pjm.2000.192.1
Pinelis I: L'Hospital type results for monotonicity, with applications. Journal of Inequalities in Pure and Applied Mathematics 2002,3(1, article 5):1–5.
Pinelis I: On L'Hospital-type rules for monotonicity. Journal of Inequalities in Pure and Applied Mathematics 2006,7(2, article 40):1–19.
Biernacki M, Krzyż J: On the monotonity of certain functionals in the theory of analytic functions. Annales Universitatis Mariae Curie-Skłodowska 1955, 9: 135–147.
Ponnusamy S, Vuorinen M: Asymptotic expansions and inequalities for hypergeometric functions. Mathematika 1997,44(2):278–301. 10.1112/S0025579300012602
Alzer H, Qiu S-L: Monotonicity theorems and inequalities for the complete elliptic integrals. Journal of Computational and Applied Mathematics 2004,172(2):289–312. 10.1016/j.cam.2004.02.009
Kuang JC: Applied Inequalities. 3rd edition. Shangdong Science and Technology Press, Jinan City, China; 2004.
Sándor J: On the identric and logarithmic means. Aequationes Mathematicae 1990,40(2–3):261–270.
Alzer H: Ungleichungen für Mittelwerte. Archiv der Mathematik 1986,47(5):422–426. 10.1007/BF01189983
Stolarsky KB: The power and generalized logarithmic means. The American Mathematical Monthly 1980,87(7):545–548. 10.2307/2321420
Zhu L: From chains for mean value inequalities to Mitrinovic's problem II. International Journal of Mathematical Education in Science and Technology 2005,36(1):118–125. 10.1080/00207390412331314971
Ostle B, Terwilliger HL: A comparison of two means. Proceedings of the Montana Academy of Sciences 1957, 17: 69–70.
Leach EB, Sholander MC: Extended mean values. II. Journal of Mathematical Analysis and Applications 1983,92(1):207–223. 10.1016/0022-247X(83)90280-9
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhu, L. Generalized Lazarevic's Inequality and Its Applications—Part II. J Inequal Appl 2009, 379142 (2009). https://doi.org/10.1155/2009/379142
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/379142
 , then
, then 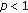 and
and 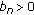 . Let
. Let  for
for  we have that
we have that 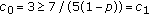 and
and 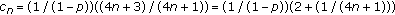 is decreasing for
is decreasing for 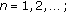 so
so  is decreasing for
is decreasing for  and
and  is decreasing on
is decreasing on  by Lemma 2.2. Hence
by Lemma 2.2. Hence 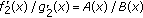 is decreasing on
is decreasing on 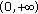 and
and  is decreasing on
is decreasing on  by Lemma 2.1. Thus
by Lemma 2.1. Thus 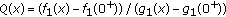 is decreasing on
is decreasing on  by Lemma 2.1.
by Lemma 2.1. , then
, then 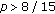 . Let
. Let 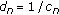 for
for  we have that
we have that 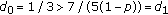 and
and  is decreasing for
is decreasing for  so
so  is decreasing for
is decreasing for  and
and  is decreasing on
is decreasing on  by Lemma 2.2. Hence
by Lemma 2.2. Hence 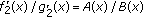 is increasing on
is increasing on 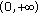 and
and 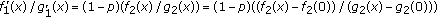 is decreasing on
is decreasing on 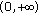 by Lemma 2.1. Thus
by Lemma 2.1. Thus 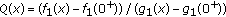 is decreasing on
is decreasing on 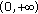 by Lemma 2.1.
by Lemma 2.1.