- Research Article
- Open access
- Published:
General System of 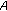 -Monotone Nonlinear Variational Inclusions Problems with Applications
-Monotone Nonlinear Variational Inclusions Problems with Applications
Journal of Inequalities and Applications volume 2009, Article number: 364615 (2009)
Abstract
We introduce and study a new system of nonlinear variational inclusions involving a combination of  -Monotone operators and relaxed cocoercive mappings. By using the resolvent technique of the
-Monotone operators and relaxed cocoercive mappings. By using the resolvent technique of the  -monotone operators, we prove the existence and uniqueness of solution and the convergence of a new multistep iterative algorithm for this system of variational inclusions. The results in this paper unify, extend, and improve some known results in literature.
-monotone operators, we prove the existence and uniqueness of solution and the convergence of a new multistep iterative algorithm for this system of variational inclusions. The results in this paper unify, extend, and improve some known results in literature.
1. Introduction
Recently, Fang and Huang [1] introduced a new class of  -monotone mappings in the context of solving a system of variational inclusions involving a combianation of
-monotone mappings in the context of solving a system of variational inclusions involving a combianation of  -monotone and strongly monotone mappings based on the resolvent operator techniques. The notion of the
-monotone and strongly monotone mappings based on the resolvent operator techniques. The notion of the  -monotonicity has revitalized the theory of maximal monotone mappings in several directions, especially in the domain of applications. Verma [2] introduced the notion of
-monotonicity has revitalized the theory of maximal monotone mappings in several directions, especially in the domain of applications. Verma [2] introduced the notion of  -monotone mappings and its applications to the solvability of a system of variational inclusions involving a combination of
-monotone mappings and its applications to the solvability of a system of variational inclusions involving a combination of  -monotone and strongly monotone mappings. As Verma point out "the class of
-monotone and strongly monotone mappings. As Verma point out "the class of  -monotone mappings generalizes
-monotone mappings generalizes  -monotone mappings. On the top of that,
-monotone mappings. On the top of that,  -monotonicity originates from hemivariational inequalities, and emerges as a major contributor to the solvability of nonlinear variational problems on nonconvex settings." and as a matter of fact, some nice examples on
-monotonicity originates from hemivariational inequalities, and emerges as a major contributor to the solvability of nonlinear variational problems on nonconvex settings." and as a matter of fact, some nice examples on  -monotone (or generalized maximal monotone) mappings can be found in Naniewicz and Panagiotopoulos [3] and Verma [4]. Hemivariational inequalities—initiated and developed by Panagiotopoulos [5]—are connected with nonconvex energy functions and turned out to be useful tools proving the existence of solutions of nonconvex constrained problems. It is worthy noting that
-monotone (or generalized maximal monotone) mappings can be found in Naniewicz and Panagiotopoulos [3] and Verma [4]. Hemivariational inequalities—initiated and developed by Panagiotopoulos [5]—are connected with nonconvex energy functions and turned out to be useful tools proving the existence of solutions of nonconvex constrained problems. It is worthy noting that  -monotonicity is defined in terms of relaxed monotone mappings—a more general notion than the monotonicity or strong monotonocity—which gives a significant edge over the
-monotonicity is defined in terms of relaxed monotone mappings—a more general notion than the monotonicity or strong monotonocity—which gives a significant edge over the  -monotonocity. Very recently, Verma [6] studied the solvability of a system of variational inclusions involving a combination of
-monotonocity. Very recently, Verma [6] studied the solvability of a system of variational inclusions involving a combination of  -monotone and relaxed cocoercive mappings using resolvent operator techniques of
-monotone and relaxed cocoercive mappings using resolvent operator techniques of  -monotone mappings. Since relaxed cocoercive mapping is a generalization of strong monotone mappings, the main result in [6] is more general than the corresponding results in [1, 2].
-monotone mappings. Since relaxed cocoercive mapping is a generalization of strong monotone mappings, the main result in [6] is more general than the corresponding results in [1, 2].
Inspired and motivated by recent works in [1, 2, 6], the purpose of this paper is to introduce a new mathematical model, which is called a general system of  -monotone nonlinear variational inclusion problems, that is, a family of
-monotone nonlinear variational inclusion problems, that is, a family of  -monotone nonlinear variational inclusion problems defined on a product set. This new mathematical model contains the system of inclusions in [1, 2, 6], the variational inclusions in [7, 8], and some variational inequalities in literature as special cases. By using the resolvent technique for the
-monotone nonlinear variational inclusion problems defined on a product set. This new mathematical model contains the system of inclusions in [1, 2, 6], the variational inclusions in [7, 8], and some variational inequalities in literature as special cases. By using the resolvent technique for the  -monotone operators, we prove the existence and uniqueness of solution for this system of variational inclusions. We also prove the convergence of a multistep iterative algorithm approximating the solution for this system of variational inclusions. The result in this paper unifies, extends, and improves some results in [1, 2, 6–8] and the references therein.
-monotone operators, we prove the existence and uniqueness of solution for this system of variational inclusions. We also prove the convergence of a multistep iterative algorithm approximating the solution for this system of variational inclusions. The result in this paper unifies, extends, and improves some results in [1, 2, 6–8] and the references therein.
2. Preliminaries
We suppose that  is a real Hilbert space with norm and inner product denoted by
is a real Hilbert space with norm and inner product denoted by  and
and  , respectively,
, respectively,  denotes the family of all the nonempty subsets of
denotes the family of all the nonempty subsets of  . If
. If 
 be a set-valued operator, then we denote the effective domain
be a set-valued operator, then we denote the effective domain  of
of  as follows:
as follows:

Now we recall some definitions needed later.
Definition 2.1 (see [2, 6, 7]).
Let  be a single-valued operator and let
be a single-valued operator and let 
 be a set-valued operator.
be a set-valued operator.  is said to be
is said to be
(i) -relaxed monotone, if there exists a constant
-relaxed monotone, if there exists a constant  such that
such that

(ii) -monotone with a constant
-monotone with a constant  if
if
(a) is
is  -relaxed monotone,
-relaxed monotone,
(b) is maximal monotone for
is maximal monotone for  (i.e.,
(i.e.,  , for all
, for all  ).
).
Remark 2.2.
If  ,
,  , then the definition of
, then the definition of  -monotonicity is that of
-monotonicity is that of  -monotonicity in [1, 8]. It is easy to know that if
-monotonicity in [1, 8]. It is easy to know that if  ( the identity map on
( the identity map on  ), then the definition of
), then the definition of  -monotone operators is that of maximal monotone operators. Hence, the class of
-monotone operators is that of maximal monotone operators. Hence, the class of  -monotone operators provides a unifying frameworks for classes of maximal monotone operators,
-monotone operators provides a unifying frameworks for classes of maximal monotone operators,  -monotone operators. For more details about the above definitions, please refer to [1–8] and the references therein.
-monotone operators. For more details about the above definitions, please refer to [1–8] and the references therein.
It follow from [3, Lemma  ] we know that if
] we know that if  is a reflexive Banach space with
is a reflexive Banach space with  its dual, and
its dual, and  be
be  -strongly monotone and
-strongly monotone and  is a locally Lipschitz such that
is a locally Lipschitz such that  is
is  -relaxed monotone, then
-relaxed monotone, then  is
is  -monotone with a constant
-monotone with a constant  .
.
Definition 2.3 (see [1, 7, 8]).
Let  , be two single-valued operators.
, be two single-valued operators.  is said to be
is said to be
(i)monotone if

(ii)strictly monotone if  is monotone and
is monotone and

(iii) -strongly monotone if there exists a constant
-strongly monotone if there exists a constant  such that
such that

(iv) -Lipschitz continuous if there exists a constant
-Lipschitz continuous if there exists a constant  such that
such that

(v) -strongly monotone with respect to
-strongly monotone with respect to  if there exists a constant
if there exists a constant  such that
such that

Definition 2.4 . (see [2]).
Let  be a
be a  -strongly monotone operator and let
-strongly monotone operator and let  be an
be an  -monotone operator. Then the resolvent operator
-monotone operator. Then the resolvent operator  is defined by
is defined by

We also need the following result obtained by Verma [2].
Lemma 2.5.
Let  be a
be a  -strongly monotone operator and let
-strongly monotone operator and let  be an
be an  -monotone operator. Then, the resolvent operator
-monotone operator. Then, the resolvent operator  is Lipschitz continuous with constant
is Lipschitz continuous with constant  for
for  , that is,
, that is,

One needs the following new notions.
Definition 2.6.
Let  be Hilbert spaces and
be Hilbert spaces and  denote the norm of
denote the norm of  , also let
, also let  and
and  be two single-valued mappings:
be two single-valued mappings:
(i) is said to be
is said to be  -Lipschitz continuous in the first argument if there exists a constant
-Lipschitz continuous in the first argument if there exists a constant  such that
such that

(ii) is said to be monotone with respect to
is said to be monotone with respect to  in the first argument if
in the first argument if

(iii) is said to be
is said to be  -strongly monotone with respect to
-strongly monotone with respect to  in the first argument if there exists a constant
in the first argument if there exists a constant  such that
such that

(iv) is said to be
is said to be  -cocoercive with respect to
-cocoercive with respect to  in the first argument if there exists a constant
in the first argument if there exists a constant  such that
such that

(v) is said to be
is said to be  -relaxed cocoercive with respect to
-relaxed cocoercive with respect to  in the first argument if there exists a constant
in the first argument if there exists a constant  such that
such that

(vi) is said to be
is said to be  -relaxed cocoercive with respect to
-relaxed cocoercive with respect to  in the first argument if there exists a constant
in the first argument if there exists a constant  such that
such that

In a similar way, we can define the Lipschitz continuity and the strong monotonicity (monotonicity), relaxed cocoercivity (cocoercivity) of  with respect to
with respect to  in the
in the  th argument
th argument  .
.
3. A System of Set-Valued Variational Inclusions
In this section, we will introduce a new system of nonlinear variational inclusions in Hilbert spaces. In what follows, unless other specified, for each  , we always suppose that
, we always suppose that  is a Hilbert space with norm denoted by
is a Hilbert space with norm denoted by  ,
,  ,
,  are single-valued mappings, and
are single-valued mappings, and  is a nonlinear mapping. We consider the following problem of finding
is a nonlinear mapping. We consider the following problem of finding  such that for each
such that for each  ,
,

Below are some special cases of (3.1).
If  , then (3.1) becomes the following problem of finding
, then (3.1) becomes the following problem of finding  such that
such that

However, (3.2) is called a system of set-valued variational inclusions introduced and researched by Fang and Huang [1, 9] and Verma [2, 6].
If  , then (3.1) becomes the following variational inclusion with an
, then (3.1) becomes the following variational inclusion with an  -monotone operator, which is to find
-monotone operator, which is to find  such that
such that

problem (3.3) is introduced and studied by Fang and Huang [8]. It is easy to see that the mathematical model (2) studied by Verma [7] is a variant of (3.3).
4. Existence of Solutions and Convergence of an Iterative Algorithm
In this section, we will prove existence and uniqueness of solution for (3.1). For our main results, we give a characterization of the solution of (3.1) as follows.
Lemma 4.1.
For  , let
, let  be a strictly monotone operator and let
be a strictly monotone operator and let  be an
be an  -monotone operator. Then
-monotone operator. Then  is a solution of (3.1) if and only if for each
is a solution of (3.1) if and only if for each  ,
,

where  is a constant.
is a constant.
Proof.
It holds that  is a solution of (3.1)
is a solution of (3.1)

Let  .
.
Theorem 4.2.
For  , let
, let  be
be  -strongly monotone and let
-strongly monotone and let  -Lipschitz continuous,
-Lipschitz continuous,  be an
be an  -monotone operator with a constant
-monotone operator with a constant  , let
, let  be a single-valued mapping such that
be a single-valued mapping such that  is
is  -relaxed cocoercive monotone with respect to
-relaxed cocoercive monotone with respect to  and
and  -Lipschitz continuous in the
-Lipschitz continuous in the  th argument,
th argument,  is
is  -Lipschitz continuous in the
-Lipschitz continuous in the  th arguments for each
th arguments for each  . Suppose that there exist constants
. Suppose that there exist constants  such that
such that

Then, (3.1) admits a unique solution.
Proof.
For  and for any given
and for any given  , define a single-valued mapping
, define a single-valued mapping  by
by

for any  .
.
For any  , it follows from (4.4) and Lemma 2.5 that for
, it follows from (4.4) and Lemma 2.5 that for  ,
,

For  , since
, since  is
is  -Lipschitz continuous,
-Lipschitz continuous,  is
is  -relaxed cocoercive with respected to
-relaxed cocoercive with respected to  and
and  -Lipschitz continuous in the
-Lipschitz continuous in the  th argument, we have
th argument, we have

For  , since
, since  is
is  -Lipschitz continuous in the
-Lipschitz continuous in the  th arguments (
th arguments ( ), we have
), we have

It follows from (4.5)–(4.7) that for each  ,
,

Hence,

where

Define  on
on  by
by  , for all
, for all  . It is easy to see that
. It is easy to see that  is a Banach space. For any given
is a Banach space. For any given  , define
, define  by
by

for all  .
.
By (4.3), we know that  , it follows from (4.9) that
, it follows from (4.9) that

This shows that  is a contraction operator. Hence, there exists a unique
is a contraction operator. Hence, there exists a unique  , such that
, such that

that is, for  ,
,

By Lemma 4.1,  is the unique solution of (3.1). This completes this proof.
is the unique solution of (3.1). This completes this proof.
Corollary 4.3.
For  , let
, let  be
be  -strongly monotone and
-strongly monotone and  -Lipschitz continuous, let
-Lipschitz continuous, let  be an
be an  -monotone operator, let
-monotone operator, let  be a single-valued mapping such that
be a single-valued mapping such that  is
is  -strongly monotone with respect to
-strongly monotone with respect to  and
and  -Lipschitz continuous in the
-Lipschitz continuous in the  th argument,
th argument,  is
is  -Lipschitz continuous in the
-Lipschitz continuous in the  th arguments for each
th arguments for each  . Suppose that there exist constants
. Suppose that there exist constants  such that
such that

Then, problem (3.1) admits a unique solution.
Remark 4.4.
Theorem 4.2 and Corollary 4.3 unify, extend, and generalize the main results in [1, 2, 6–8].
5. Iterative Algorithm and Convergence
In this section, we will construct some multistep iterative algorithm for approximating the unique solution of (3.1) and discuss the convergence analysis of these Algorithms.
Let  and
and  be two real sequences of nonnegative numbers that satisfy the following conditions:
be two real sequences of nonnegative numbers that satisfy the following conditions:
(1) and
and  ,
,
(2)
then  converges to 0 as
converges to 0 as  .
.
Algorithm 5.2.
For  , let
, let  be the same as in Theorem 4.2. For any given
be the same as in Theorem 4.2. For any given  , define a multistep iterative sequence
, define a multistep iterative sequence  by
by

where

Theorem 5.3.
For  , let
, let  be the same as in Theorem 4.2. Assume that all the conditions of theorem 4.1 hold. Then
be the same as in Theorem 4.2. Assume that all the conditions of theorem 4.1 hold. Then  generated by Algorithm 5.2 converges strongly to the unique solution
generated by Algorithm 5.2 converges strongly to the unique solution  of (3.1).
of (3.1).
Proof.
By Theorem 4.2, problem (3.1) admits a unique solution  , it follows from Lemma 4.1 that for each
, it follows from Lemma 4.1 that for each  ,
,

It follows from (4.3), (5.1) and (5.3) that for each  ,
,

For  , since
, since  is
is  -Lipschitz continuous,
-Lipschitz continuous,  is
is  -relaxed cocoercive with respected to
-relaxed cocoercive with respected to  , and
, and  -Lipschitz is continuous in the
-Lipschitz is continuous in the  th argument, we have
th argument, we have

For  , since
, since  is
is  -Lipschitz continuous in the
-Lipschitz continuous in the  th arguments (
th arguments ( ), we have
), we have

It follows from (5.4)–(5.6) that for  ,
,

Hence,

where

It follows from hypothesis (4.3) that  .
.
Let  . Then, (5.8) can be rewritten as
. Then, (5.8) can be rewritten as  By (5.2), we know that
By (5.2), we know that  , it follows from Lemma 5.1 that
, it follows from Lemma 5.1 that

Therefore,  converges to the unique solution
converges to the unique solution  of (3.1). This completes the proof.
of (3.1). This completes the proof.
References
Fang YP, Huang NJ: -monotone operators and system of variational inclusions. Communications on Applied Nonlinear Analysis 2004,11(1):93–101.
Verma RU: -monotonicity and applications to nonlinear variational inclusion problems. Journal of Applied Mathematics and Stochastic Analysis 2004,17(2):193–195.
Naniewicz Z, Panagiotopoulos PD: Mathematical Theory of Hemivariational Inequalities and Applications, Monographs and Textbooks in Pure and Applied Mathematics. Volume 188. Marcel Dekker, New York, NY, USA; 1995.
Verma RU: Nonlinear variational and constrained hemivariational inequalities involving relaxed operators. Zeitschrift für Angewandte Mathematik und Mechanik 1997,77(5):387–391. 10.1002/zamm.19970770517
Panagiotopoulos PD: Hemivariational Inequalities and Their Applications in Mechanics and Engineering. Springer, New York, NY, USA; 1993.
Verma RU: General system of -monotone nonlinear variational inclusion problems with applications. Journal of Optimization Theory and Applications 2006,131(1):151–157. 10.1007/s10957-006-9133-5
Verma RU: General nonlinear variational inclusion problems involving -monotone mappings. Applied Mathematics Letters 2006,19(9):960–963. 10.1016/j.aml.2005.11.010
Fang Y-P, Huang N-J: -monotone operator and resolvent operator technique for variational inclusions. Applied Mathematics and Computation 2003,145(2–3):795–803. 10.1016/S0096-3003(03)00275-3
Fang Y-P, Huang N-J: A new system of variational inclusions with -monotone operators in Hilbert spaces. Computers & Mathematics with Applications 2005,49(2–3):365–374. 10.1016/j.camwa.2004.04.037
Acknowledgment
This study was supported by grants from National Natural Science Foundation of China (project no. 70673012, no. 70741028 and no. 90924030), China National Social Science Foundation (project no. 08CJY026).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Peng, JW., Zhao, LJ. General System of 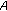 -Monotone Nonlinear Variational Inclusions Problems with Applications.
J Inequal Appl 2009, 364615 (2009). https://doi.org/10.1155/2009/364615
-Monotone Nonlinear Variational Inclusions Problems with Applications.
J Inequal Appl 2009, 364615 (2009). https://doi.org/10.1155/2009/364615
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/364615